考虑温升梯度影响的表贴式高速永磁电机转子强度分析
2022-01-27陈亮亮冯惊鸿祝长生伍家驹李志农
陈亮亮, 冯惊鸿, 熊 茹, 祝长生, 伍家驹, 李志农
(1. 南昌航空大学 无损检测技术教育部重点实验室, 南昌 330063; 2. 南昌航空大学 信息工程学院, 南昌 330063;3. 国网江西省电力有限公司供电服务管理中心, 南昌 330077; 4. 浙江大学 电气工程学院, 杭州 310027)
表贴式高速永磁电机具有结构简单、效率高、功率密度高等优点,在压缩机、飞轮储能、高速离心机、高速机床等领域应用广泛[1-2]。高剩磁、高矫顽力以及高磁能积的稀土永磁材料广泛应用于高速永磁电机[3]。表贴式永磁电机的永磁体结构主要有整体式和分块式两类。与分块式结构相比,整体永磁体具有结构简单、便于加工、机械强度高等优点,但其永磁材料的利用率相对较低。整体结构的永磁体又可进一步分为实心圆柱结构及空心圆环结构。
稀土永磁材料的抗压强度较大而抗拉强度很小,而电机高速运行时将产生强大的离心力,其性质为拉力,巨大的离心力容易破坏永磁体,因此,需要在永磁体外设置高强度的保护套。高强度保护套主要有复合材料及非导磁金属材料两类,常用的复合材料有碳纤维和玻璃纤维,而常用的非导磁金属材料则有钛合金及高强度合金钢等。复合材料护套为各向异性材料,非导磁金属护套则可看作各向同性材料[4-5]。与复合材料护套相比,非导磁金属护套的强度分析过程相对简单、精度高,且易于永磁体的散热,有助于避免永磁体过热而退磁,但也存在涡流损耗的问题[6-8]。
实际中,常采用有限元法和解析法对高速永磁电机的转子强度进行分析,确保电机在高速运行状态下永磁体内的应力能够满足要求。有限元法精度高,但建模困难,计算量大[9-11]。解析法具有计算量小、效率高、适合转子强度的优化设计等优点,但解析解的推导较为困难,尤其是复杂结构转子的解析解[12]。
针对碳纤维复合材料护套固定的永磁转子的强度解析计算问题,文献[13-15]进行了研究。Binder等[13]提出了碳纤维护套圆柱型永磁转子的环向应力及接触压强的解析解,该解析解未考虑材料各向异性及转子发热的影响。同时考虑碳纤维材料各向异性及转子温度等因素对转子应力的影响,陈亮亮等[14]研究了碳纤维护套圆环型永磁转子的强度解析解。针对表贴式高速永磁电机在高速高温工况下的转子强度分析问题,刘威等[15]提出考虑轴间填充物的电机转子强度的解析模型。
文献[16-20]研究了非导磁金属护套固定的永磁转子的强度解析建模问题。Borisavljevic 等[16]提出了非导磁金属护套圆柱型永磁转子的应力解析解。忽略转子发热的影响,王继强等[17]和程文杰等[18]提出了圆柱及圆环两种整体永磁转子的强度解析解,并通过有限元法验证了解析解的有效性。张超等[19]从平面应变的角度研究了非导磁金属护套保护下圆环型永磁体转子的强度解析解。针对分块永磁转子的强度分析问题,陈亮亮等[20]提出了未考虑温度影响的强度解析解。
忽略永磁体温升对转子强度的影响,张凤阁等[21]分析了非导磁金属护套和碳纤维护套两种保护方式下圆柱型整体永磁转子的强度解析解。针对含极间填充块的分块结构永磁转子,Chen等[22]提出了非导磁金属护套及碳纤维护套永磁转子的强度解析解的统一模型。
已有的转子强度解析解在考虑温度影响时通常近似认为转子各部分的温度相同,把转子温升看作常数,然而在工程实际中转子内的温度往往是不均匀的,温度沿径向呈梯度分布,即转子温升存在一定的梯度。Du等[23]采用有限元法研究了转子温升梯度对分块永磁转子应力的影响,结果表明,如果把转子温升看作常数,则永磁体的应力计算结果将产生13.3%的误差。因此,转子强度解析解需要进一步考虑转子温升梯度分布的影响。此外,在以往的研究过程中,主要采用有限元法对解析解进行验证,缺乏电机高速运行的试验验证。
针对存在温升梯度的转子强度分析问题,本文基于弹性力学中的平面应力模型,推导了永磁转子径向位移、径向应力、环向应力以及等效Mises应力的解析解,并分别通过有限元仿真及电机高速运行试验对解析解的有效性进行验证。在此基础上,进一步深入分析护套厚度、过盈量、转速及温度等参数对转子强度的影响,总结非导磁金属护套整体永磁转子强度的变化规律。
1 转子结构
图1所示为非导磁金属护套圆环型永磁转子的结构,转子主要包括永磁体、转子铁芯及非导磁金属护套三个部分。转子各部分的尺寸标注如图2所示,Ror为转子铁芯的外半径;Rim和Rom为圆环型永磁体的内半径及外半径;Ris和Ros为非导磁金属护套的内半径及外半径。为了使永磁体免受高速离心力的破坏,永磁体与非导磁金属护套间常采用过盈配合。
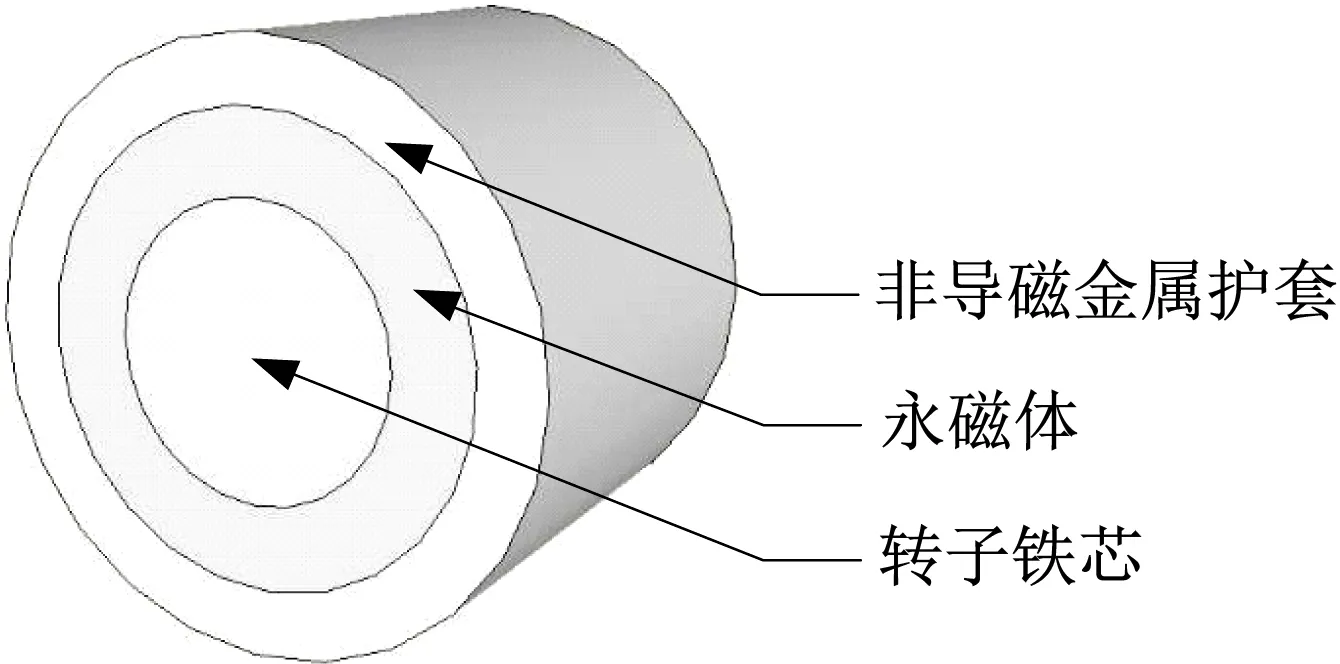
图1 永磁转子结构Fig.1 Structure of the PM rotor
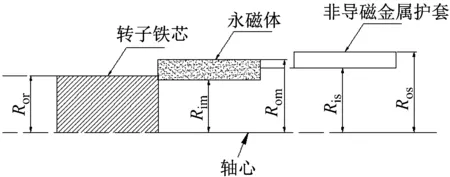
图2 转子尺寸标注Fig.2 Dimensions of the rotor
假设永磁体与转子铁芯和非导磁金属护套之间的过盈量分别为δ1及δ2,即:
(1)
2 转子强度解析解
将转子应力简化为平面应力问题,先假设永磁体与转子铁芯和非导磁金属护套接触面的接触压强分别为P1和P2;接着分别求解非导磁金属护套、永磁体和转子铁芯的平衡方程、物理方程及几何方程,得到转子各部件的应力和位移的解析解;最后通过转子各部件相互接触面的径向位移边界条件来求解接触压强P1、P2。
2.1 非导磁金属护套强度分析
如图3所示,非导磁金属护套内表面受到均匀压强P2的作用,外表面受力为零。
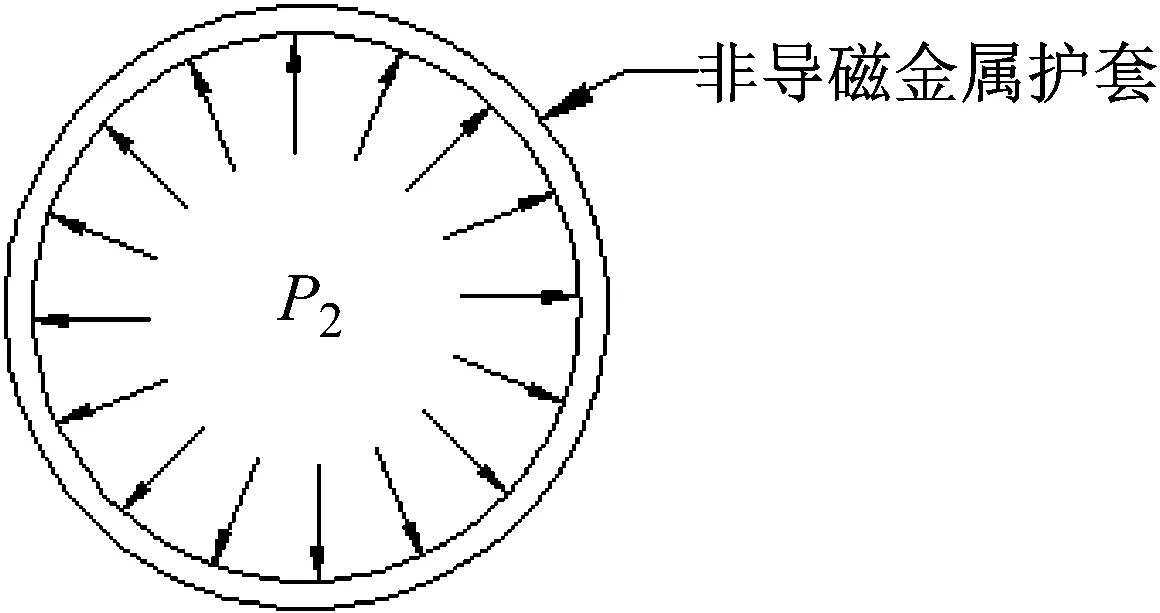
图3 非导磁金属护套受力图Fig.3 Force diagram of non-magnetic alloy sleeve
高速运行状态下,非导磁金属护套的平衡微分方程可表示为
(2)
式中:r为半径;σrs和σθs分别为非导磁金属护套的径向应力及环向应力;ρs和ω为非导磁金属护套的密度及转子角速度。
转子发热状态下非导磁金属护套的物理方程可表示为
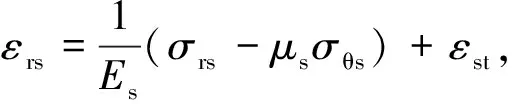
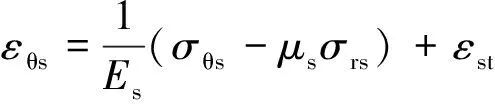
(3)
式中:Es,μs,εrs和εθs分别为非导磁金属护套的弹性模量、泊松系数、径向应变及环向应变;εst为非导磁金属护套的温升热应变,可采用以下公式来计算
εst=βs·ΔTs
(4)
式中:βs和ΔTs分别为非导磁金属护套的热膨胀系数和温升,ΔTs=Ts-Ts0;Ts0和Ts分别为非导磁金属护套在半径r处的初始温度及发热后的温度,温升ΔTs不为常数,而是沿半径方向存在一定的梯度。
非导磁金属护套的几何方程可表示为
εrs=durs/dr,εθs=urs/r
(5)
式中,urs为非导磁金属护套的径向位移,它是半径的函数。
结合非导磁金属护套的平衡微分方程、物理方程和几何方程可得到考虑转速及转子温升影响的径向位移us(r),径向应力σrs(r)、环向应力σθs(r)及等效Mises应力σsMises(r),分别为
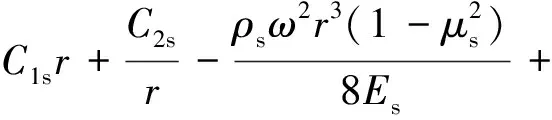
(6)
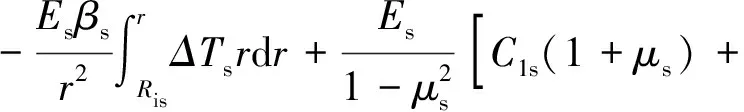
(7)
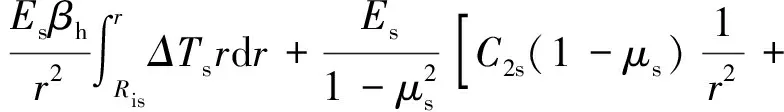
βsΔTsEs
(8)
(9)
式中,C1s和C2s为待定系数,由应力边界条件确定。
非导磁金属护套外表面受力为零,而内表面则受到均匀压强P2的作用,在弹性力学中,以拉应力为正,压应力为负,因此,其应力边界条件可表示为
σrs(r)|r=Ris=-P2,σrs(r)|r=Ris=0
(10)
根据应力边界条件(10)可解出待定系数C1s和C2s。
2.2 永磁体强度分析
永磁体受力如图4所示,其内外表面分别受到均匀压强P1和P2的作用。
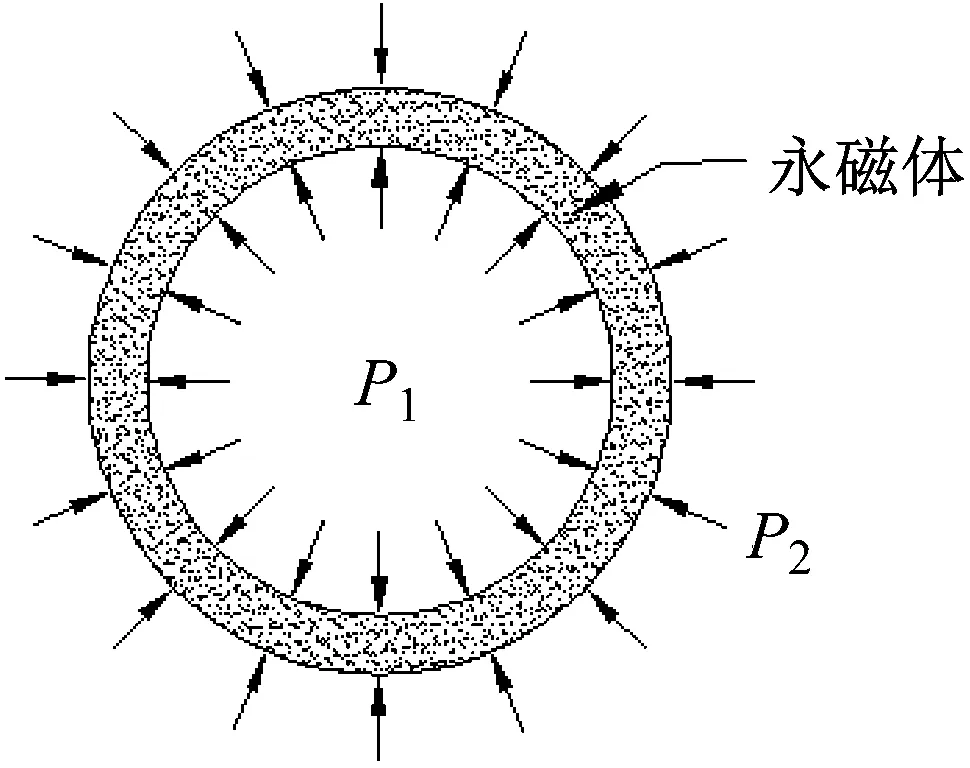
图4 永磁体受力图Fig.4 Force diagram of PM
永磁体的应力及径向位移分析方法与非导磁金属护套类似,但其应力边界条件有所不同。由永磁体受力图可知,永磁体内外表面的径向应力分别为-P1和-P2,其应力边界条件可表示为
σrm|r=Rim=-P1,σrm|r=Rom=-P2
(11)
综合永磁体的平衡微分方程、物理方程、几何方程及应力边界条件,可得到永磁体的径向位移urm(r)、径向应力σrm(r)、环向应力σθm(r)及等效Mises应力σmMises(r)。
2.3 转子铁芯强度分析
图5所示为转子铁芯受力图,转子铁芯为实心圆柱结构,其外表面受到均匀压强P1的作用。
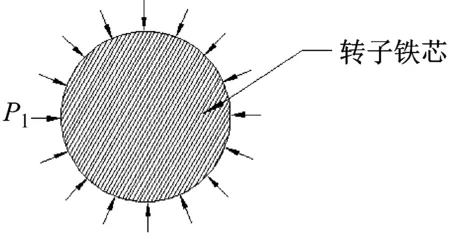
图5 转子铁芯受力图Fig.5 Force diagram of rotor core
转子铁芯的平衡微分方程、几何方程及物理方程与非导磁金属护套类似,而边界条件则有所不同。
当r=0, 转子铁芯的径向位移urr(0)=0,转子铁芯外表面受到均匀压强P1的作用,因此,转子铁芯的边界条件可表示为
urr|r=0=0,σrr|r=Ror=-P1
(12)
根据转子铁芯的平衡微分方程、物理方程、几何方程及边界条件,可得到转子铁芯的径向位移urr(r)、径向应力σrr(r)及环向应力σθr(r)及等效Mises应力σrMises(r)的表达式,分别为
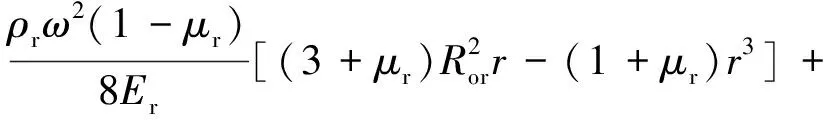
(13)
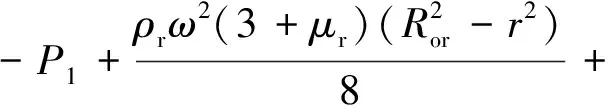
(14)
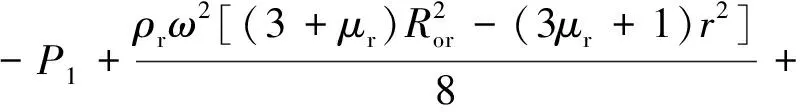
(15)
(16)
当转子铁芯的温升ΔTr为常数时,式(13)~(15)可简化为
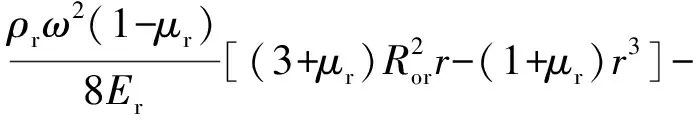
(17)
(18)
(19)
式(13)~(15)表明,当转子铁芯的温升ΔTr不为常数时,转子温升在转子铁芯内会同时产生额外的径向位移和温升热应力;式(17)~(19)表明,当转子铁芯的温升ΔTr为常数时,转子温升仅在转子铁芯内产生额外的径向位移,但没有额外的温升热应力。可以证明,转子发热对非导磁金属护套和永磁体的应力及径向位移的影响也有类似规律,具体分析过程与转子铁芯相似,恕不赘述。由此可见,在分析永磁转子的应力分布时,需要进一步考虑温度梯度的影响。
2.4 接触压强P1,P2的求解
根据非导磁金属护套、永磁体以及转子铁芯相互接触面的径向位移边界条件得到接触压强P1及P2。在非导磁金属护套径向位移表达式urs(r)中令r=Ris得到非导磁金属护套内表面的径向位移urs(Ris);在永磁体径向位移表达式urm(r)中分别令r=Rim及r=Rom得到永磁体内外表面的径向位移urm(Rim)和urm(Rom);在转子铁芯径向位移表达式urm(r)中令r=Ror得到转子铁芯外表面处的径向位移urr(Ror)。
根据转子各部件接触面的径向位移边界条件有:永磁体内表面的径向位移urm(Rim)减去转子铁芯外表面的径向位移urr(Ror)等于静态过盈量δ1;非导磁金属护套内表面的径向位移urs(Ris)减去永磁体外表面的径向位移urm(Rom)应该等于静态过盈量δ2,即转子各部件接触面的径向位移边界条件可表示为
(20)
求解方程式(20)可得到接触压强P1和P2。
3 有限元仿真分析
分别采用解析法和有限元来分析某高速永磁电机的转子应力,电机额定电压为380 V,额定功率为75 kW,额定转速为24 000 r/min,定子槽数为12,极对数为1,矽钢片厚度为0.35 mm,转子永磁体为整体圆环型结构,采用钛合金护套对永磁体进行保护。转子各部件之间的过盈量为:δ1=0,δ2=0.15 mm,表1为电机转子各部件的基本参数。
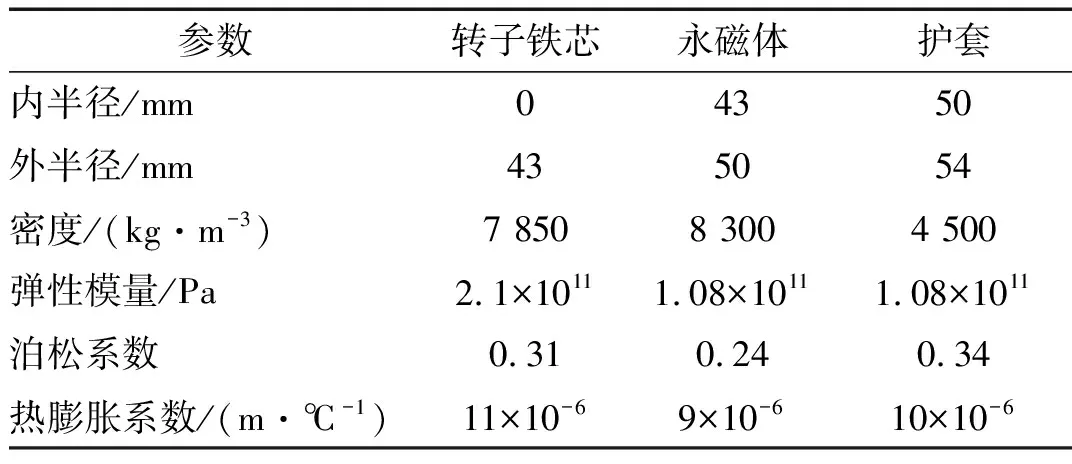
表1 永磁体转子的基本参数
分别采用解析解和有限元法计算三种运行状态下的转子应力:① 转速为零的静态,此时的应力由永磁体与非导磁金属护套间的过盈量产生;② 电机以24 000 r/min的额定转速运行,但转子尚未发热,温升为零;③ 电机以24 000 r/min的额定转速运行,转子发热且温升不为常数。
采用ANSYS仿真软件对永磁转子进行热分析,求解发热状态下转子内的温度分布。在热分析过程中,转子初始温度取20 ℃,经Ansoft仿真分析得到永磁体和非导磁金属护套的涡流损耗分别为48 W及22 W,由于转子铁芯采用很薄的电硅钢片制成,再加上非导磁金属护套的屏蔽作用,转子铁芯损耗很小,这里忽略不计,电机定转子间气隙的对流散热系数取28 W/(m2·℃)。图6为ANSYS热分析得到的永磁转子的温度分布。

图6 永磁体转子的温度分布Fig.6 Temperature distribution of the PM rotor with non- magnetic alloy sleeve
图6表明,转子铁芯内的温度基本为一常数,但永磁体和护套内的温度则不是常数,而是随着半径的增加,温度逐渐减小,即温升沿着永磁体和护套的半径方向呈现梯度分布。
采用曲线拟合法对热分析结果进行拟合,可得到转子各部件的温升表达式
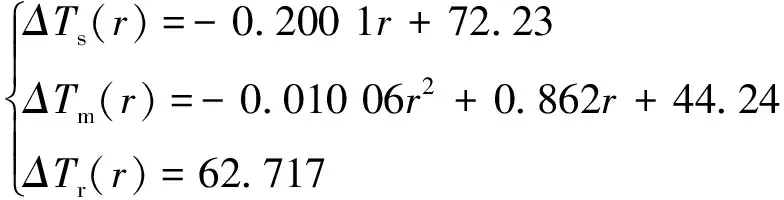
(21)
式中,半径r和温升的单位分别为mm和摄氏度。本节中,电机在第三种运行状态下的转子温升为式(21)。转子温升表达式(21)是初始温度为常温20 ℃时的计算结果,虽然当初始温度改变时,转子温升表达式会有所差别,但这里转子温升的求解思路具有通用性。
3.1 永磁体应力分析
三种运行状态下,有限元法得到的永磁体径向应力云图如图7~9所示,解析法和有限元法得到的沿半径方向永磁体径向应力分布如图10所示。在图10中,实线表示解析法的计算结果,星线则代表有限元法的计算结果,拉力为正,压力为负,符号σ表示应力。由于转子是轴对称的,为方便表达,这里仅给出四分之一圆周的应力云图。
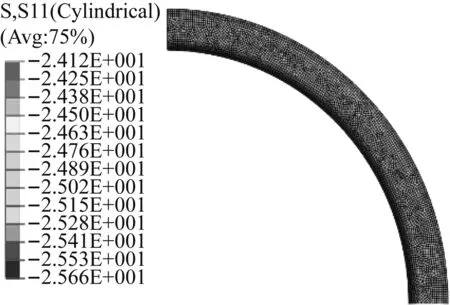
图7 静态时永磁体的径向应力云图Fig.7 Radial stress contour of PM at static state
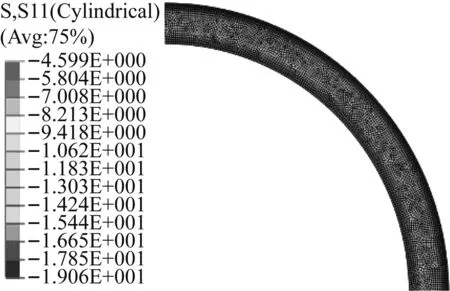
图8 高速无温升时永磁体的径向应力云图Fig.8 Radial stress contour of PM at high speed state
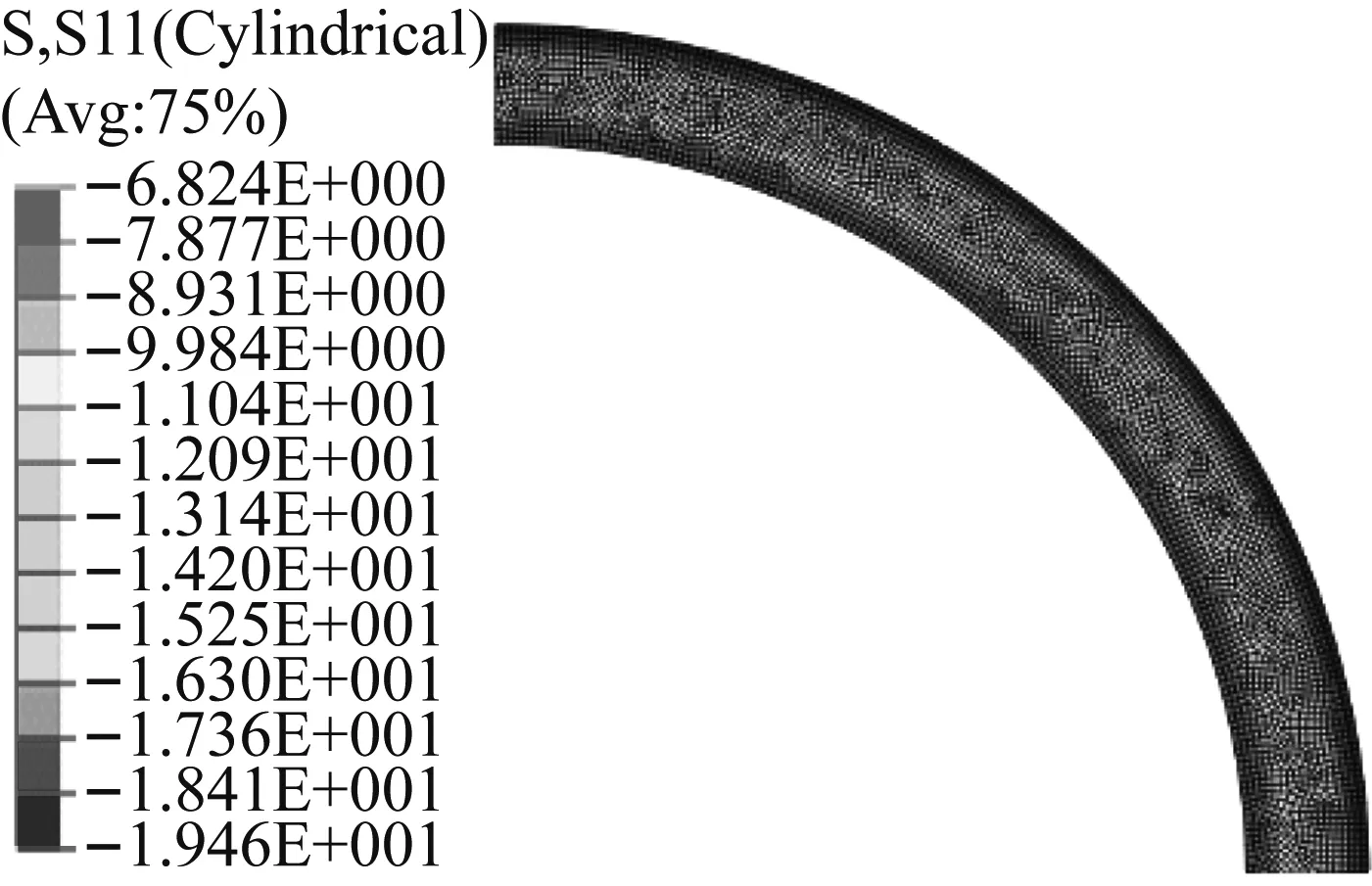
图9 高速且转子发热时永磁体的径向应力云图Fig.9 Radial stress contour of PM at hot running state

图10 永磁体径向应力分布Fig.10 Radial stress distribution of PM
图7~10表明,解析解和有限元法的计算结果相吻合,解析解能够准确计算永磁体的径向应力。三种运行状态下,永磁体的径向应力均保持为压力(负值)。静态时,径向应力沿半径方向略有减小。高速运行时,由于离心力的影响,永磁体的径向应力大幅减小,此时,径向应力沿半径方向逐渐增加,最大径向应力出现在外表面。转子温升使得永磁体的径向应力有所增加,且径向应力沿半径方向的分布规律与转子高速运行但尚未发热状态类似。
图11~13所示为三种运行状态下的永磁体环向应力云图,两种方法得到的沿半径方向永磁体环向应力分布如图14所示。结果表明,两种方法得到的永磁体环向应力也相一致。静态时,永磁体的环向应力为压力。高速运行状态下巨大的离心力使得永磁体内的环向应力由压力变为拉力,转子发热使得永磁体的环向拉应力进一步增加。在高速且转子发热状态下的永磁体内表面处,永磁体的环向拉应力达到最大值,约为18 MPa,其值小于永磁体的抗拉强度(约为35 MPa),永磁体不会被拉应力所破坏。
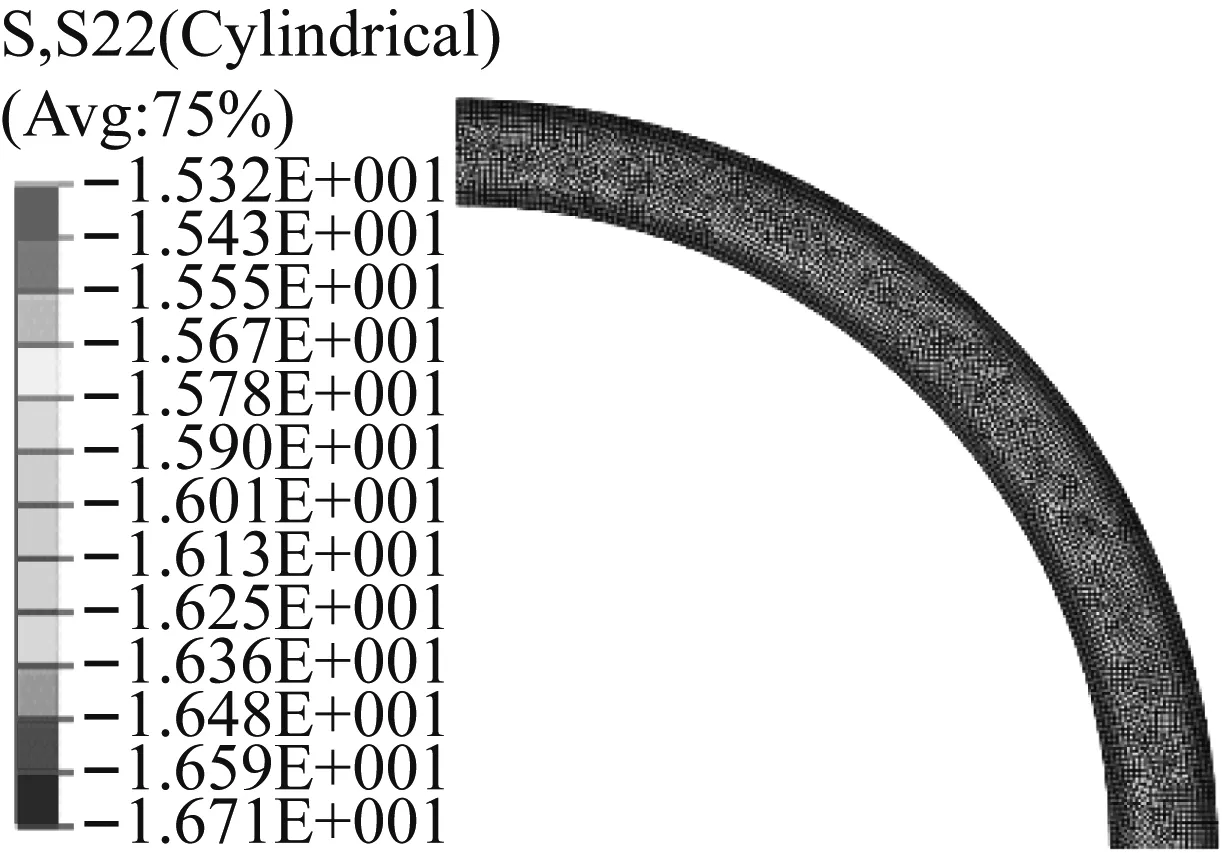
图11 静态时永磁体的环向 应力云图
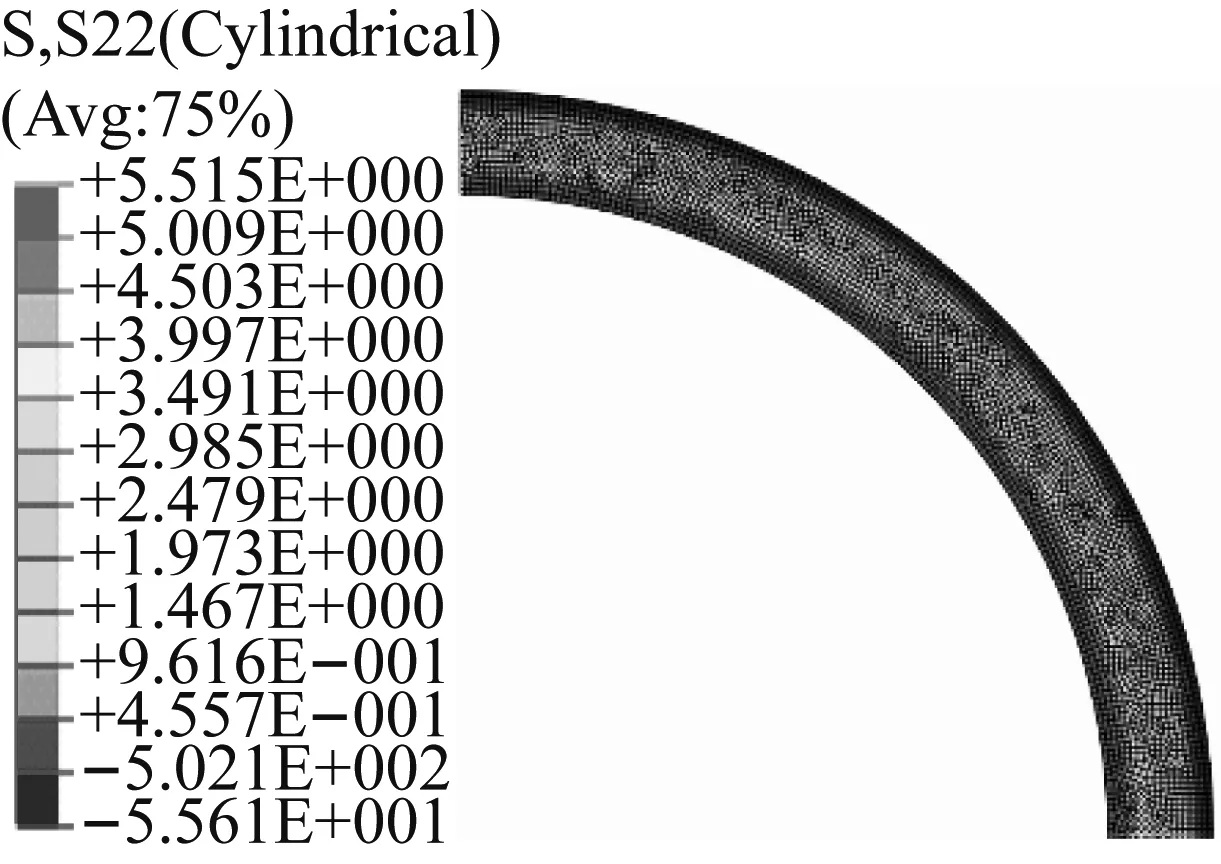
图12 高速无温升时永磁体的环向应力云图
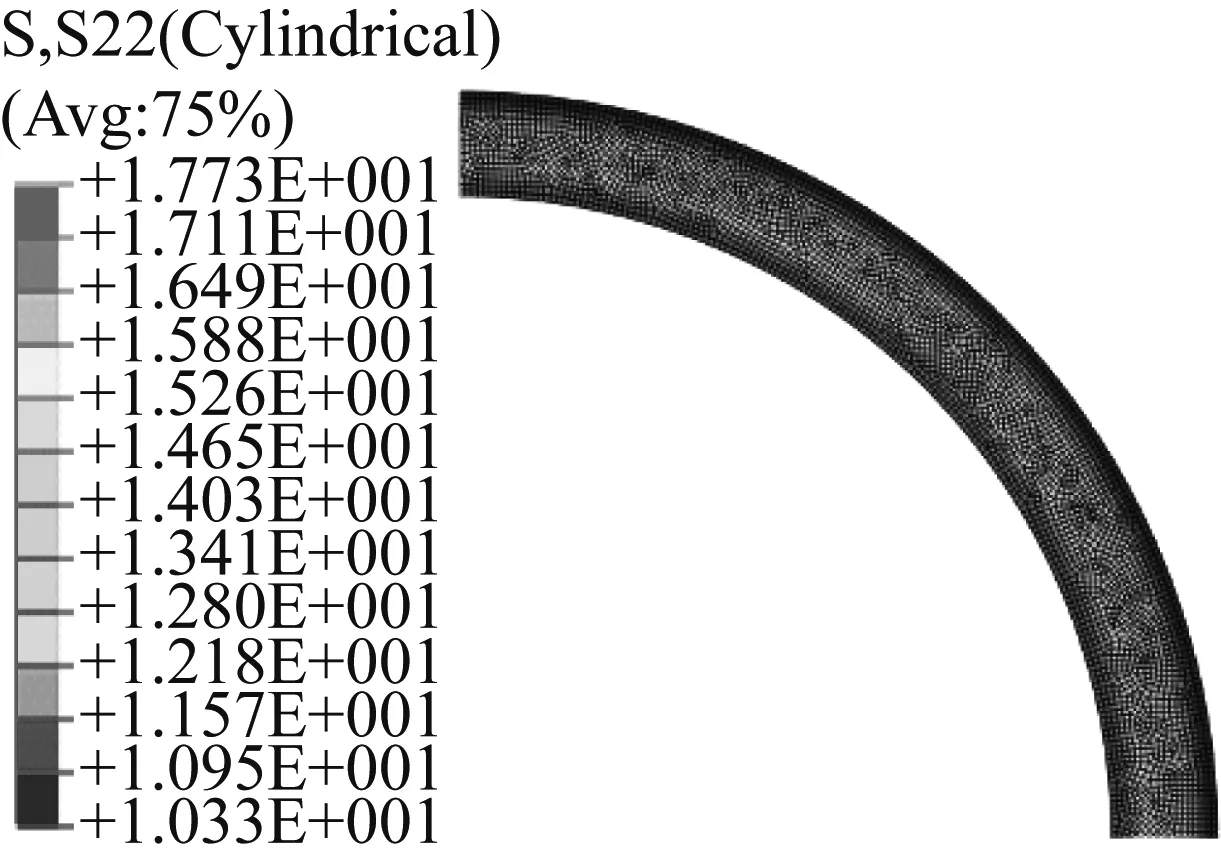
图13 高速且转子发热时永磁体的环向应力云图
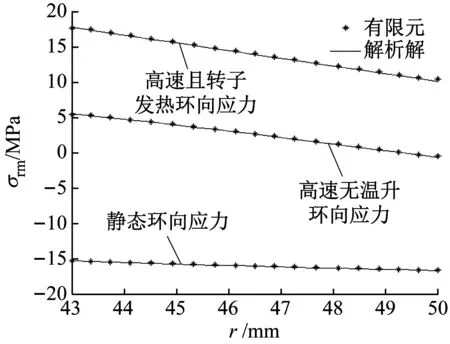
图14 永磁体环向应力分布
3.2 非导磁金属护套应力分析
限于篇幅原因,这里仅给出非导磁金属护套Mises等效应力的计算结果。Mises等效应力是径向应力和环向应力的综合计算结果,可反映径向应力和环向应力的计算精度。
三种运行状况下,有限元法得到的非导磁金属护套Mises等效应力云图如图15~17所示,解析法和有限元法得到的沿非导磁金属护套半径方向的Mises等效应力分布如图18所示。
图15~18表明,解析解和有限元法得到的非导磁金属护套Mises等效应力相一致,解析解也能准确计算非导磁金属护套的Mises等效应力。由于永磁体与非导磁金属护套之间采用过盈配合,静态时非导磁金属护套内具有一定的预应力,其性质为拉力。高速离心力及转子发热均使得非导磁金属护套内的等效Mises应力增加,与转子温升相比,高速离心力对护套应力的影响更大。三种运行状态下,非导磁金属护套的Mises等效应力均沿着半径方向而逐渐减小,最大应力出现在护套内表面。在本例中,非导磁金属护套的Mises等效应力最大值约为335 MPa,远小于非导磁金属护套的抗拉强度(约为1 000 MPa),不会对护套造成损坏。
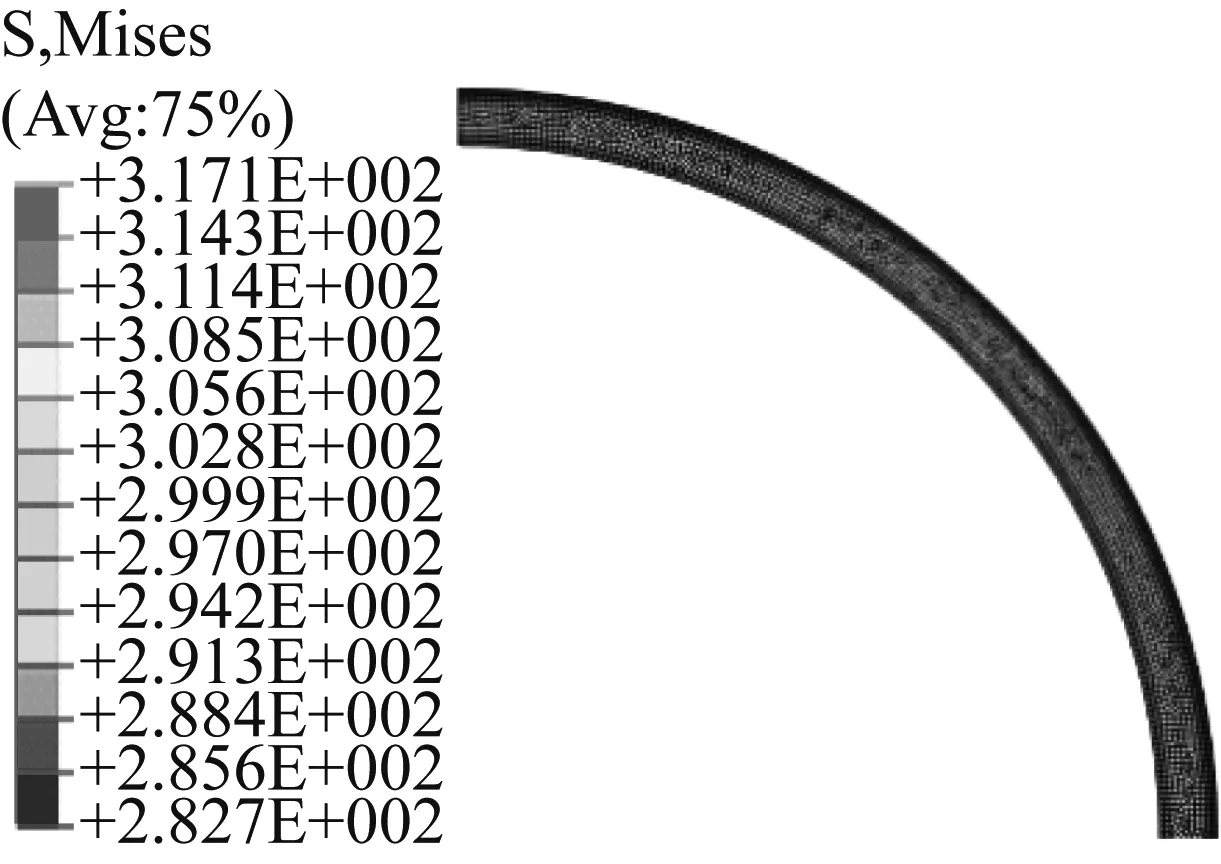
图15 静态时护套的Mises等效应力云图
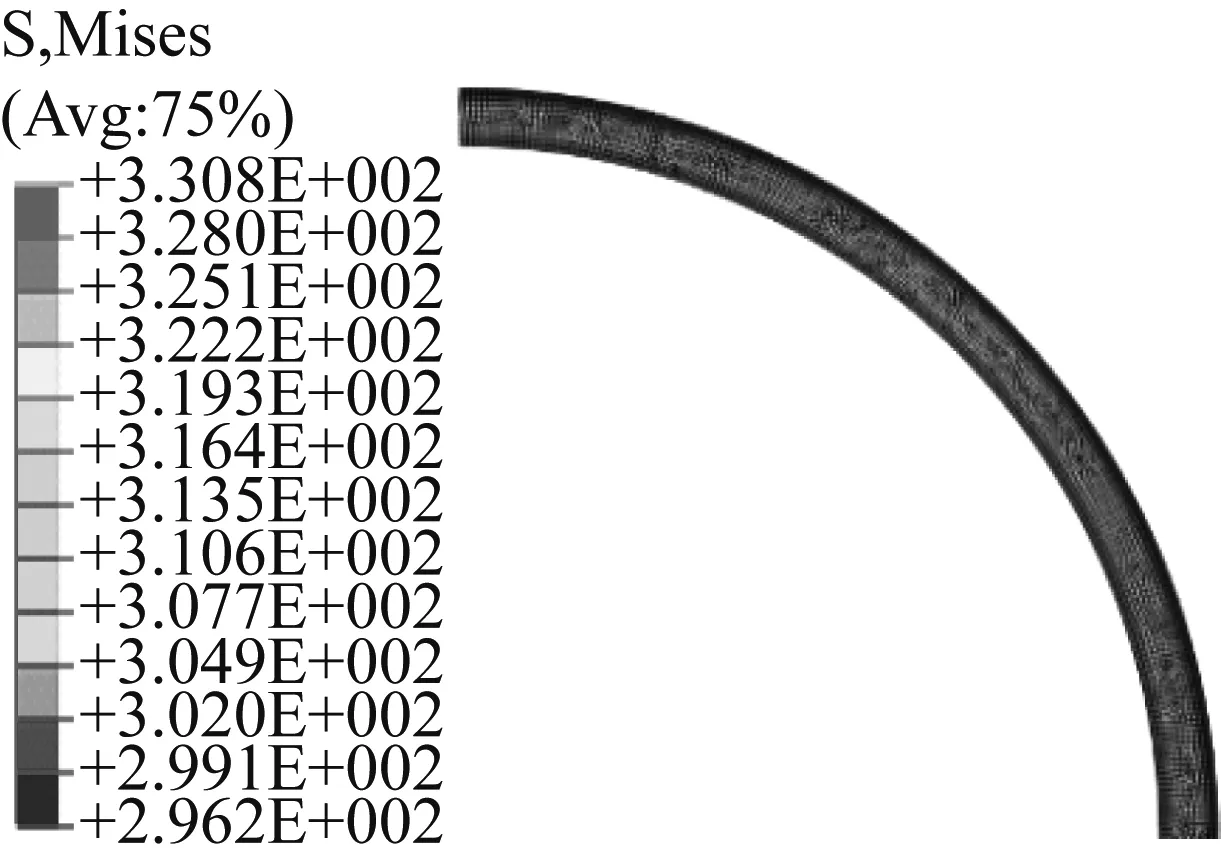
图16 高速无温升时护套的Mises等效应力云图
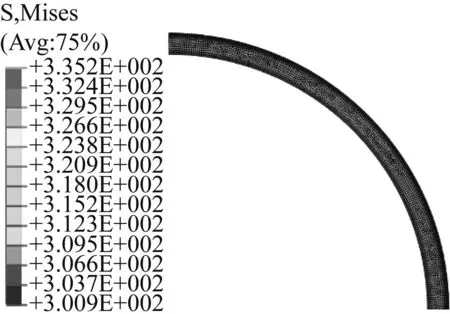
图17 高速且转子发热时护套的Mises等效应力云图
仿真分析的结果表明,本文推导的解析解能够准确计算考虑过盈配合、转速及温升梯度等因素影响下非导磁金属护套永磁体转子的应力。
4 试验分析
通过试验来直接测量电机转子内的应力比较困难,但我们可以借助电机的高速运行试验来间接验证解析解的计算结果。高速永磁电机的试验平台如图19所示,电机参数与第三节的仿真参数一致。电机转子采用主动电磁轴承支撑,dSPACE控制器和开关功率放大器用于控制主动电磁轴承线圈中的电流,进而产生悬浮转子的电磁力。
在空载状态下,通过变频器将电机逐渐加速至额定转速,并持续运行一段时间。整个试验过程中电机稳定运行,未发现异常,图20为额定转速下的电流波形。结果表明,在24 000 r/min的额定转速下,电机的相电流波形为正弦波,电机能够在额定转速下可靠工作,永磁体未被高速离心力及转子温升热应力所破坏。因此,基于本文提出的解析解而设计的转子强度能够满足实际运行要求,解析解的应力分析结果正确。
5 分析与讨论
基于本文提出的转子强度解析解,深入研究静态过盈量δ2、非导磁金属护套厚度、转速及温升等参数对转子应力的影响。为简化分析过程,近似将转子温升当作常数,即,ΔTr=ΔTm=ΔTs=常数。静态时的接触压强(P1,P2)和非导磁金属护套最大Mises等效应力σmax随静态过盈量和护套厚度的变化关系分别如图21和22所示。接触压强(P1,P2)和非导磁金属护套最大Mises等效应力σmax随转速和温升的变化关系分别如图23和24所示。
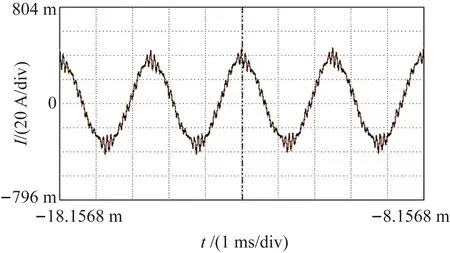
图20 额定转速下的相电流波形Fig.20 Waveform of phase current at rated speed
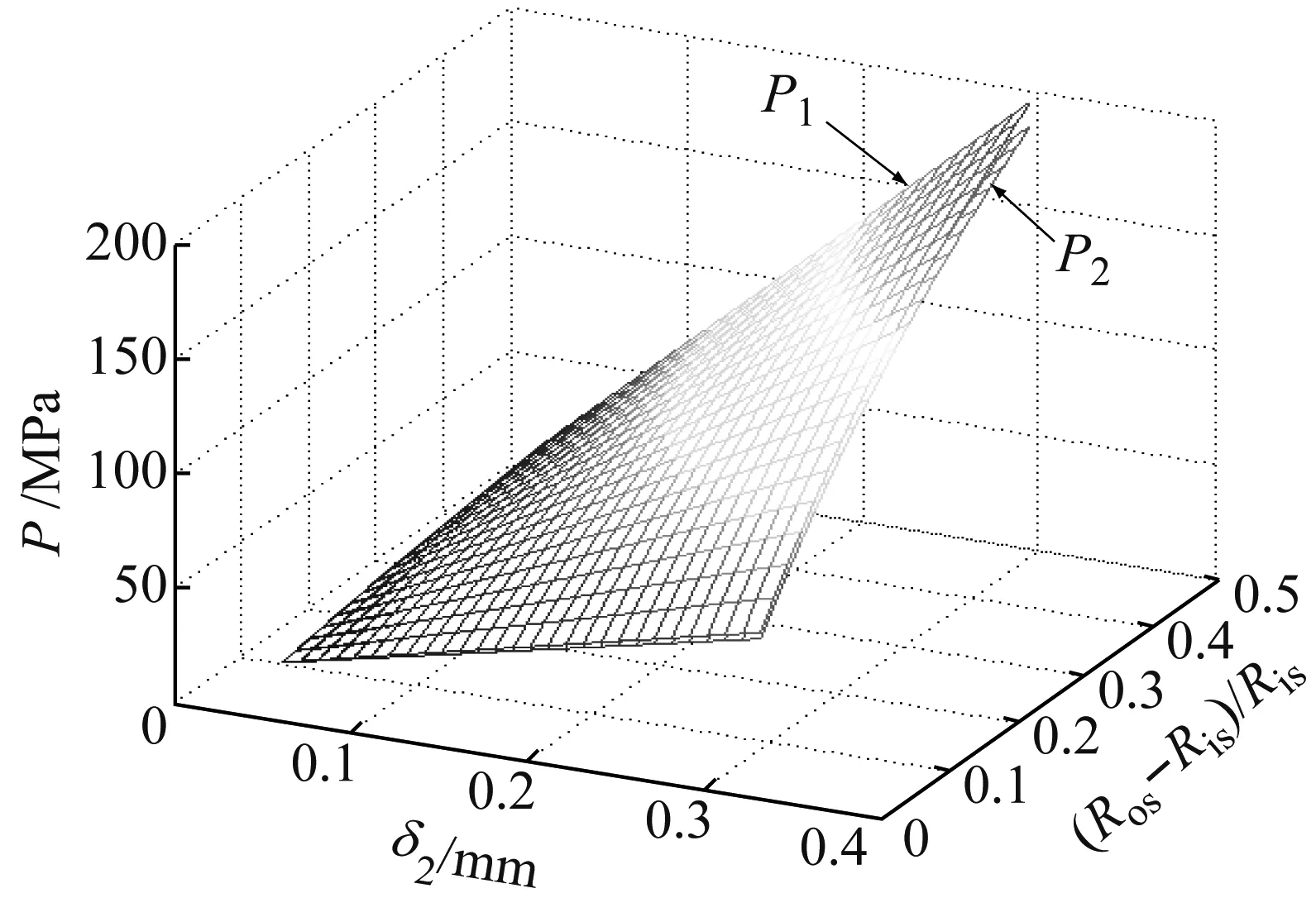
图21 接触压强与静态过盈量、护套厚度的关系Fig.21 Relationships between contact pressures and sleeve thickness, static interference fit
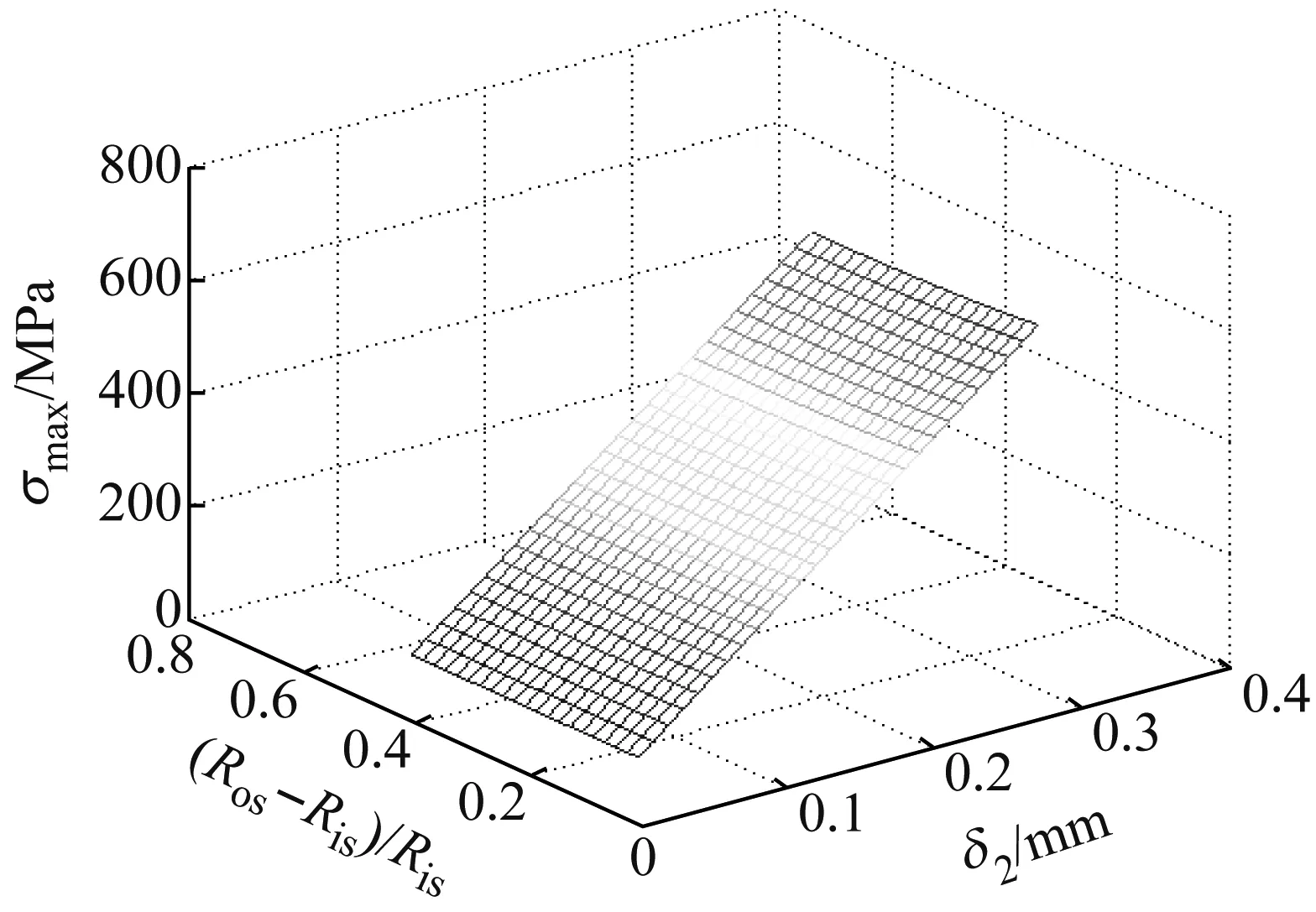
图22 护套最大等效应力与静态过盈量、护套厚度的关系
图21和22表明,当其他参数恒定时,接触压强(P1、P2)和非导磁金属护套的最大Mises等效应力随着静态过盈量δ2的增加而大幅增大;接触压强(P1、P2)随着非导磁金属护套厚度的增加而大幅增加,但护套最大Mises等效应力却随着护套厚度的增加而略有减小。静态时,永磁体与非导磁金属护套之间的接触压强P2略小于转子铁芯与永磁体之间的接触压强P1,且两者均随着过盈量δ2和护套厚度的增加而增大。
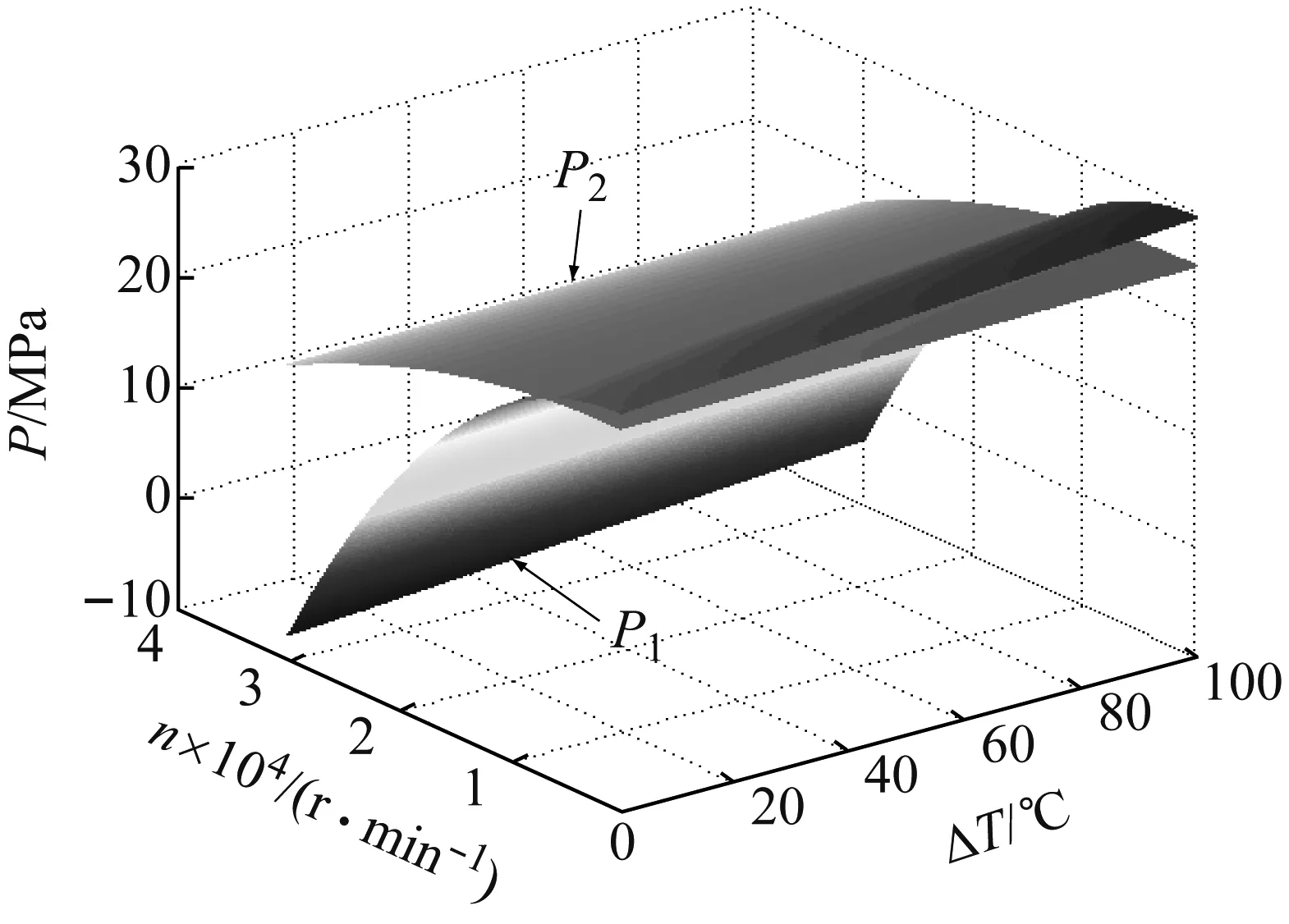
图23 接触压强与转速、温升的关系Fig.23 Relationships between contact pressures and rotational speed, temperature rise
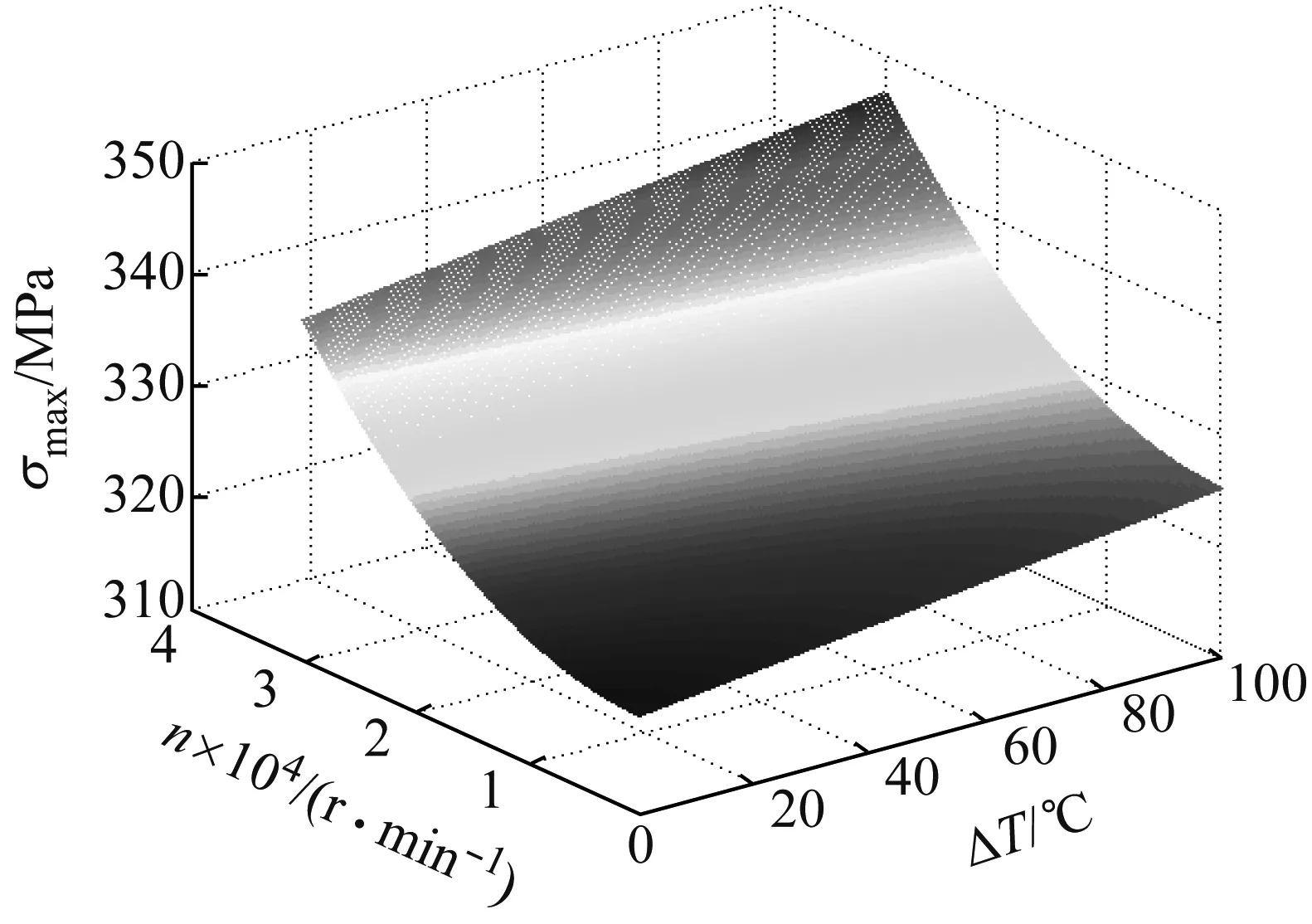
图24 护套最大等效应力与转速、温升的关系
图23和24表明,随着转速的增加, 非导磁金属护套最大Mises等效应力大幅增加,但接触压强(P1、P2)逐渐减小,与P2相比,P1受转速影响更大;随着转子温度的增加,非导磁金属护套最大Mises等效应力和接触压强(P1、P2)均逐渐增加,且接触压强P1受温度的影响较P2大。
6 结 论
基于考虑温升梯度影响的高速永磁电机转子强度解析解的理论推导、仿真和试验结果,可得出以下结论:
(1) 本文提出的解析解能够准确计算考虑温升梯度影响的非导磁金属护套高速永磁电机的转子应力,可为此类电机转子的强度分析及设计提供参考。
(2) 增加静态过盈量可增加永磁体的预压力,进而提高松脱转速,但非导磁金属护套的最大应力也随着静态过盈量的增大而大幅增加,增加静态过盈量时,需要重新校验非导磁金属护套的应力分布,确保护套的最大Mises等效应力不超过其抗拉强度。
(3) 转子发热后各点的温度并不相同,沿着永磁体和护套的半径方向转子温升存在一定的梯度,温升梯度将会在转子中产生额外的温升热应力,分析高速永磁电机转子的应力分布需要进一步考虑温升梯度的影响。
