基于冲压试验的聚乙烯力学性能预测
2022-01-27范峻铭
常 频,张 毅,孙 峰,乔 亮,范峻铭
(1.中国石油大学(华东)储运与建筑工程学院,山东 青岛 266580;2.深圳市燃气集团股份有限公司,广东 深圳 518000;3.深圳市燃气输配及高效利用工程技术研究中心,广东 深圳 518000)
0 前言
冲压试验技术作为一种无损检测的新型试验技术,发展非常迅速,该技术的优点之一是只需要对微小的试样材料进行试验就可以得出材料的诸多性能[1⁃2]。从在役设备上微损取样,通过冲压试验获得的材料的性能变化状况,既可以对在役设备的安全状况进行评估,又可以对设备寿命进行预测。随着冲压试验技术的改进与发展,其在测试金属材料基本力学性能方面得到了较广泛的应用[1,3⁃22]。Mao[3]通过对 HT⁃60、PCA、HT⁃9、SUS304和A533B这5种材料进行冲压试验,得到了屈服强度与屈服载荷的经验关系式;韩浩[11]对11种材料进行了冲压试验,通过采用两段曲线拟合的方法确定屈服载荷并建立了屈服强度与屈服载荷的线性关系式。近些年来,冲压试验也被用于表征聚合物材料的力学性能。Rodriguez等[23⁃24]使用冲压试验测试了聚丙烯、聚对苯二甲酸乙二醇酯、聚乳酸和乙烯⁃乙烯醇共聚物4种聚合物的力学性能,通过对比单轴拉伸试验中的应力⁃应变曲线和冲压试验中的载荷⁃位移曲线,建立了弹性模量与冲压试验中载荷⁃位移曲线初始斜率以及屈服强度与屈服载荷的联系;Maspoch等[25]采用冲压试验对有机蒙脱石基聚乳酸薄膜(PLA/o⁃MMT)的力学性能进行分析,发现冲压试验的载荷⁃位移曲线斜率除以试样厚度所得到的值与弹性模量之间存在某种关联。
上述研究中,大多是以厚度为变量建立起最大冲压载荷与屈服强度之间的联系。本文通过对单轴拉伸试验数据和冲压试验数据进行对比,分别建立了以压头直径、压头直径的平方以及压头直径与最大冲压载荷对应位移的乘积为变量的屈服强度经验公式并对PE⁃HD单轴拉伸时的力学性能进行预测。
1 实验部分
1.1 主要原料
PE⁃HD,重均分子量为 63 069 g/mol,密度为0.940 g/cm3,棋伊耐磨材料有限公司。
1.2 主要设备及仪器
电子万能试验机,UTM5504,深圳三思纵横科技股份有限公司。
1.3 样品制备
试验所选用的材料均由PE⁃HD加工而成;在单轴拉伸试验中采用5种不同缺口半径的圆棒试样,分别为光滑圆棒试样以及缺口半径分别为20、5、2、0.5 mm的圆棒试样,记作R20、R5、R2、R0.5,其中带有缺口的试样均由直径为10 mm,长度为150 mm的圆棒试样加工而来,且最小直径为6 mm,具体尺寸如图1所示;在冲压实验中采用40 mm×40 mm×3 mm的聚乙烯平板试样进行试验,利用打孔机在距离试样边缘6 mm处打4个圆柱形孔洞,目的是通过螺栓将试样固定在压杯上,孔的直径为5 mm。

图1 PE⁃HD圆棒试样Fig.1 PE⁃HD round bar specimens
1.4 性能测试与结构表征
采用电子万能试验机对5种不同的圆棒试样进行单轴拉伸试验,试验开始前记录圆棒中间位置的直径,用试验机自带的夹具固定好试样上下两端,安装电子引伸计,利用位移控制加载方式以1 mm/min的恒定速率对圆棒试样进行拉伸直至断裂,试验机记录载荷、位移、应变;
冲压试验采用自行设计的冲压装置,如图2所示,冲压试验装置由压头、压杯、固定片以及连接体组成;试验装置与试验机通过连接体固定,压头与上方连接体固连,压杯采用中空设计与下方连接体固连;将PE⁃HD平板试样固定在压杯上,采用不同直径且倒角半径均为1 mm的压头分别以0.01、0.1、1、10、100 mm/min的恒定速率对PE⁃HD平板进行冲压,记录冲压过程中的载荷⁃位移曲线,以上试验均在室温下完成。

图2 冲压试验装置示意图Fig.2 Schematic diagram of punch test device
2 结果与讨论
2.1 缺口半径对单轴拉伸试验载荷⁃位移曲线的影响
在单轴拉伸试验中5种缺口试样均拉伸至断裂,试验过程中PE⁃HD圆棒试样出现了明显的颈缩现象,且随着缺口半径的增大颈缩现象越来越明显。试验记录了5种不同缺口半径圆棒试样的载荷变化情况,对数据进行处理,得到工程应力与位移的关系曲线,如图3所示。PE⁃HD试样的工程应力⁃位移曲线可以分为4个阶段,分别为弹性阶段、屈服阶段、颈缩阶段和应变硬化阶段。提取屈服点处的应力强度并记录在表1中。图3的结果显示PE⁃HD材料有明显的缺口效应,随着缺口半径的减小,圆棒试样的屈服应力逐渐增加,而断裂时的位移显著减小,最后的应变硬化阶段也在逐渐弱化直至完全消失。通过观察断裂后的试样形态可以发现随着缺口半径的减小,PE⁃HD圆棒试样的断裂形式逐渐从塑性断裂转变为脆性断裂。
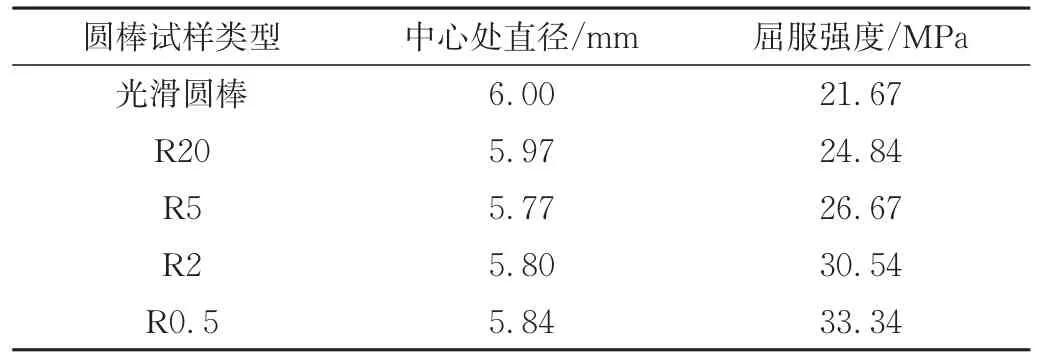
表1 单轴拉伸试验力学参数Tab.1 Mechanical parameters of uniaxial tensile test
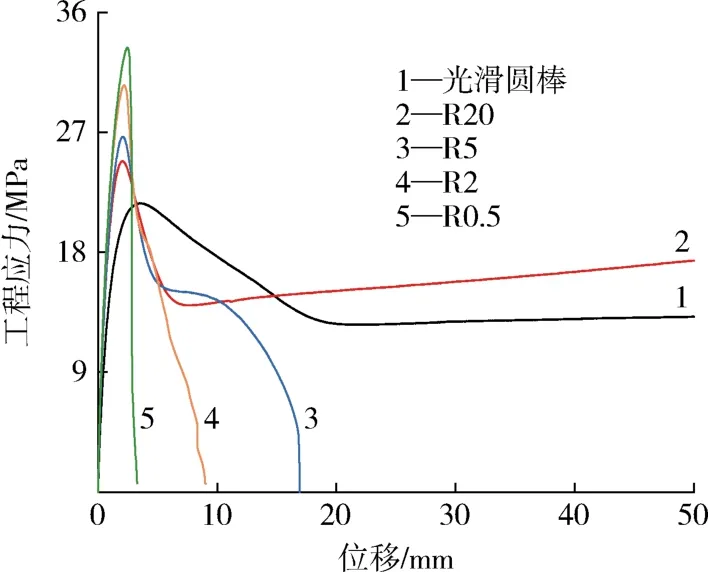
图3 不同缺口圆棒试样的工程应力⁃位移曲线Fig.3 Engineering stress⁃displacement curves of notched roundbar specimens
2.2 试验条件对冲压试验载荷⁃位移曲线的影响
冲压试验作为一种微型试样试验技术,试样的选取及试验条件的改变都会对试验结果产生较大的影响。本文采用直径分别为4、6、8、10 mm的压头以恒定冲压速度对PE⁃HD平板进行冲压试验,得到的试验结果如图4、图5所示。由试验结果可知,冲压试验的载荷⁃位移曲线可以分为弹性变形、塑性变形、颈缩、破坏断裂4个阶段。在冲压试验过程中,PE⁃HD平板试样中心处会产生一个突起的帽状结构,为延性断裂的典型特征。图4为同一压头直径下不同冲压速度的载荷⁃位移曲线,结果显示在同一压头直径下,PE⁃HD平板试样的最大载荷随着冲压速度的增大而增大,但断裂位移随冲压速度的增大而减小,表明冲压速度会对PE⁃HD平板的承载能力和延性产生一定的影响。图5为同一冲压速度下不同压头直径的载荷⁃位移曲线,结果显示在同一冲压速度下,峰值载荷随压头直径的增加而增大,且试样的断裂位移也随之增大。这表明在一定范围内压头直径越大,试样塑性变形的能力越强,PE⁃HD平板的延性越好。

图4 不同压头直径时冲压试验得出的载荷⁃位移曲线Fig.4 Load⁃displacement curves from punch tests with different indenter diameters

图5 不同冲压速度时冲压试验得到的载荷⁃位移曲线Fig.5 Load⁃displacement curves from punch tests at different punch speeds
PE⁃HD作为一种高分子聚合物,在单轴拉伸和冲压试验下得到的力学性能也与金属材料有较大的差异。在PE⁃HD冲压试验中,一般认为峰值力对应的状态为屈服状态,其对应的载荷为屈服载荷。选取冲压速度为1 mm/min时的试验进行分析,记录不同压头直径下PE⁃HD平板试样的最大冲压载荷(Fp)以及最大冲压载荷对应的位移(δ)于表2中。由表2可知,随着压头直径的增大,试样的承载能力在逐步提高。当压头直径为4 mm时发生屈服时所需位移较小,而压头直径为8、10 mm时发生屈服时所需位移较大,表明在一定程度上压头直径越小,屈服现象越会较快地发生。
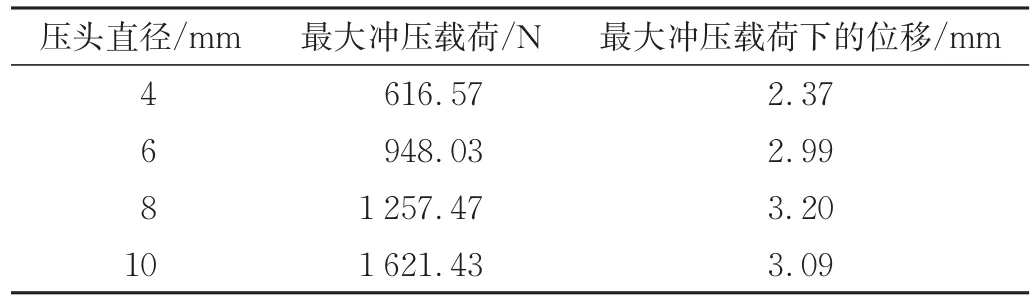
表2 冲压试验力学参数Tab.2 Mechanical parameters of punch test
2.3 单轴拉伸试验与冲压试验的关联性研究
基于以上试验结果,发现压头直径对冲压试验的结果影响较大,因此在进行线性拟合时不能忽略压头直径这一影响因素。将冲压试验中的数据与单轴拉伸试验中的力学参数进行关联,分别以压头直径、压头直径的平方以及压头直径与最大冲压载荷下位移的乘积作为变量,建立最大冲压载荷与以上3个变量的关系,得到的拟合曲线如图6所示。

图6 最大冲压载荷与不同变量的关系曲线Fig.6 Curves of the relationship between the maximum punch load and different variables
基于图6(a)的拟合公式,建立最大冲压载荷Fp与屈服强度σy的经验公式如式(1)所示:

式中Fp——最大冲压载荷,N
σy——屈服强度,MPa
A1——待定系数值
B1——待定系数值
从而单轴拉伸时的屈服强度的计算公式如式(2)所示:

当单轴拉伸试验中采用的是光滑圆棒试样时,由表1可知,屈服强度为σy=21.67MPa,将其代入式(1)并联立图6(a)的拟合公式,可得A1=7.67,B1=-52.53,将A1和B1代入到式(2),得到光滑圆棒试样的屈服强度为:

为了考虑多种变量下所得PE⁃HD屈服强度经验公式的可靠性,将图6(a)的压头直径参数变量换为压头直径的平方以及压头直径与最大冲压载荷对应的位移的乘积,分别建立最大冲压载荷与两个变量之间的关系,得到的线性拟合曲线如图6(b)、(c)所示。
基于图6(b)、(c)的结果,建立Fp与σy的经验关系式如式(4)、式(5)所示:

单轴拉伸时的屈服强度如式(6)、式(7)所示:
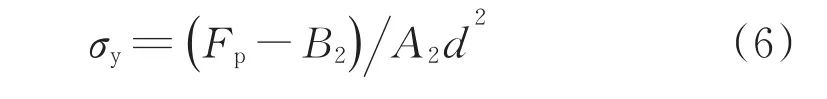

将光滑圆棒试样以及缺口半径为R20、R5、R2、R0.5圆棒试样的屈服强度分别带入式(1)、(4)、(5),可得3种经验公式的待定系数值,如表3所示。
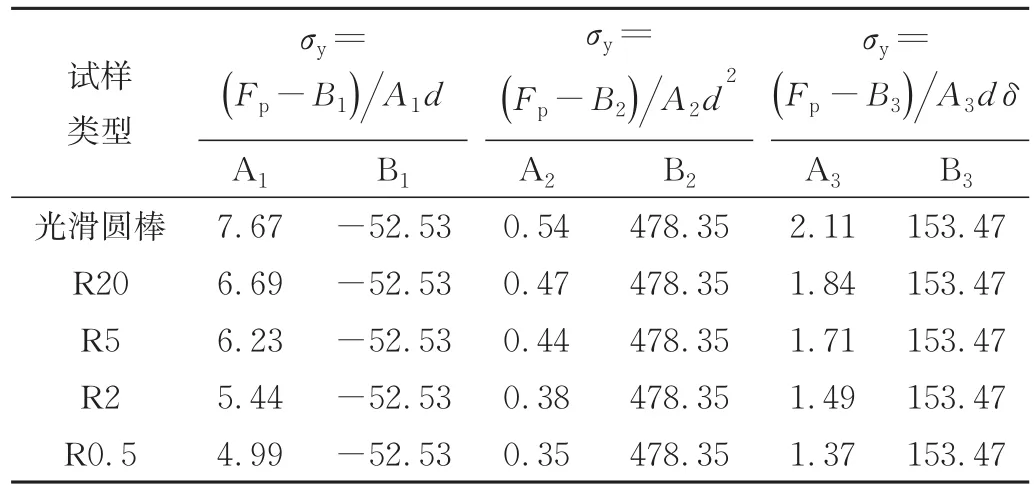
表3 3种经验公式的系数Tab.3 Undetermined coefficients of three empirical formulas
将冲压试验所得不同压头直径的最大冲压载荷分别代入到式(2)、(6)、(7),结果图7所示。为了确定3种关联式的合理性,需对数据进行统计研究。在本文中,PE⁃HD屈服强度的离散程度由标准差来表征,计算公式如式(8)所示,结果记录在表4中。
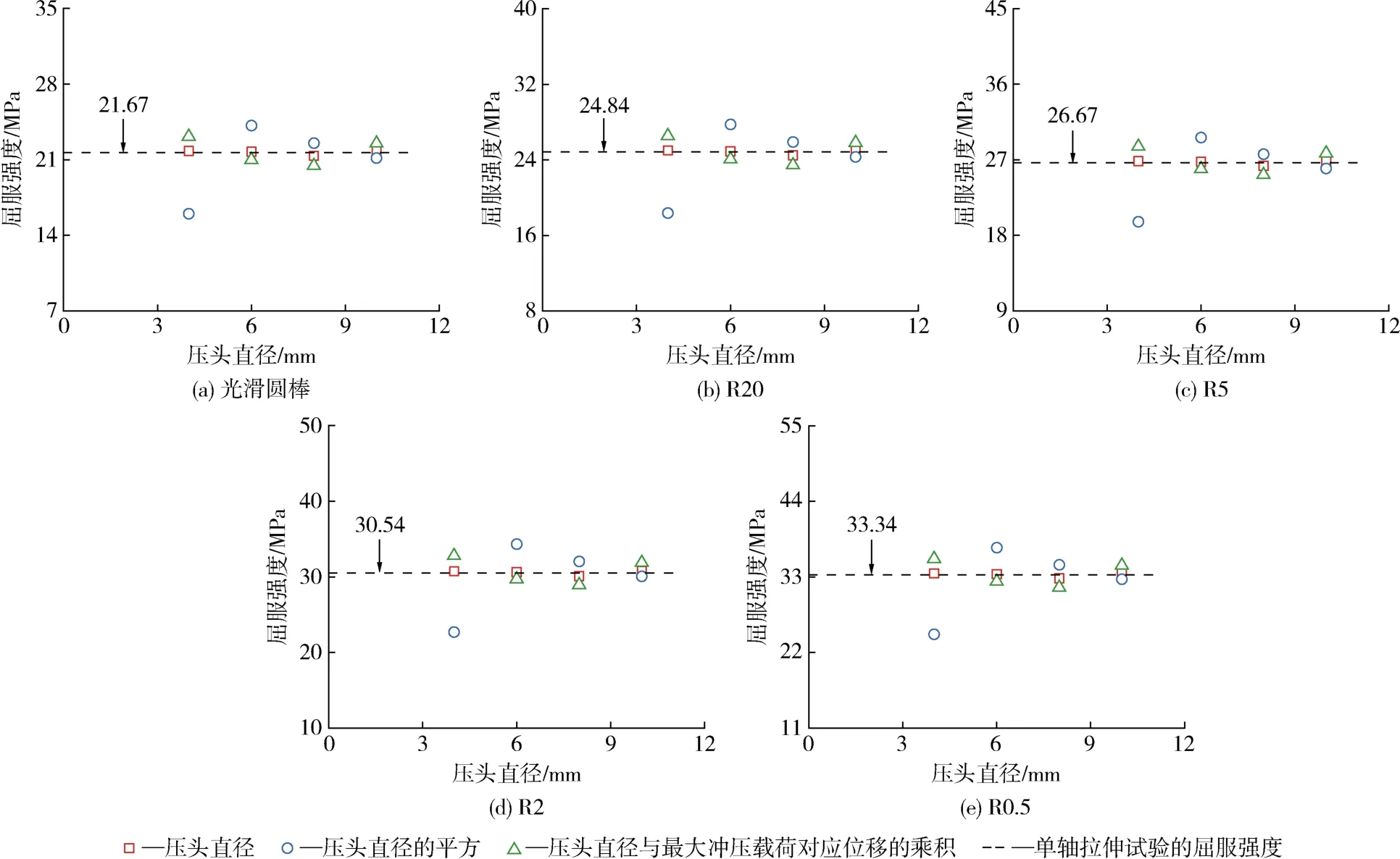
图7 3种经验公式得到的不同缺口半径下PE⁃HD的屈服强度Fig.7 Yield strength of PE⁃HD at different notch radii obtained from the three empirical formulas

表4 不同类型PE⁃HD屈服强度的标准差Tab.4 Standard deviation of yield strength for different types of PE⁃HD

式中Ri——屈服强度,MPa
n——样本编号
从以上3个关联式中可以得知:选用不同的经验公式得到的结果差异较大,对比图6中3条拟合曲线,可以发现,采用参数d参与线性拟合,决定系数R2=0.99899;采用参数d2参与线性拟合,决定系数R2=0.98844;采用参数dδ参与线性拟合,决定系数R2=0.98375。拟合的决定系数R2越接近于1,说明数据的拟合程度越好,因此使用参数d参与线性拟合得到的结果最优。同时观察表4可知,采用关联式(2)得到的PE⁃HD屈服强度变化幅度较小,即离散程度较小,采用关联式(6)得到的结果离散程度较大,不能较为准确地表征PE⁃HD的屈服强度。针对同一关联式下不同类型的PE⁃HD材料,当其为光滑圆棒试样时,所得结果的离散性最低,对于有缺口的PE⁃HD试样,随着缺口半径的减小,计算得到的标准差逐渐增大,说明缺口效应会对屈服强度的预测产生一定的影响。因此,在研究冲压试验与单轴拉伸试验的关联性时,选择经验公式(2)表征PE⁃HD光滑圆棒试样在单轴拉伸时的力学性能最为合理。
3 结论
(1)PE⁃HD材料在拉伸过程中有明显的缺口效应,具体表现为:随着缺口半径的减小,PE⁃HD圆棒试样的屈服应力逐渐增大,且断裂形态从塑性断裂逐渐转变为脆性断裂;
(2)同一压头直径下,PE⁃HD平板试样的最大载荷随冲压速度的增加而增大,但平板试样的延展性有所下降,断裂位移显著减小;同一冲压速度下,PE⁃HD平板试样的最大载荷随着压头直径的增加而增大,且平板试样的延展性增强,断裂位移明显增加;
(3)基于试验结果研究了冲压试验最大冲压载荷与单轴拉伸屈服强度之间的关联性并建立了3种不同的经验公式,其中以压头直径为变量的经验公式预测得到的屈服强度可靠性最高,可以较为准确地表征PE⁃HD的力学性能。
