电场的MATLAB可视化方法*

周群益

(广州理工学院通识教育学院 广东 广州 510540)

莫云飞

(长沙学院电子信息与电气工程学院 湖南 长沙 410022)

周丽丽

(赣南医学院信息工程学院 江西 赣州 341000)

侯兆阳

(长安大学理学院 陕西 西安 710064)

1 引言

文献[1]用MATLAB辅助电动力学教学做了有益的探索．将导体球放在匀强电场中，利用电磁场的边值关系，用二维彩色图片和色棒说明电场强度的分量和合场强的分布规律．不过，文献[1]中并没有介绍场强的数学模型，彩色图片变成黑白图片后并不鲜明．有一些教师已经在电磁学和电动力学的教学和研究中应用MATLAB[2,3]，取得了显著的成绩．这些文献并没有计算和绘图程序．文献[3]采用三维等高线表示电势，用曲面表示场强大小，用电场线和等势线表示电场，用动画演示电磁波传播的过程和电偶极子发射电磁波的过程．这些都是常用的方法，在笔者10年前出版的著作中就已经广泛采用了[4]．许多电场问题都可以表示为直角坐标系中的二元函数，将公式无量纲化，即可用MATLAB的surf指令或mesh指令画曲面，用二维和三维等高线指令contour和contour3画等势线，用流线指令streamline画电场线[5～7]．

本文以导体球放在匀强电场中形成的电场为例，根据电动力学理论建立数学模型，将公式无量纲化，用柱坐标系中的曲面表示场强的分量，用直角坐标系的曲面表示电势，用等高线指令画电场线和等势线，显示电场和电势的分布规律．文本附加的程序说明了实现方法和指令，程序设计的技巧很有启示作用．

2 匀强电场中放置导体球后的电场

在真空中有一匀强电场E0，放置一个半径为a的导体球，图1所示为未发生静电感应时的状态，静电感应之前，电场线穿过导体球．由于静电感应，导体球的左右两边会产生感应电荷，使球内的场强为零，球外的电场会发生形变．由于电场具有轴对称性，取球心为原点O，取E0方向为极轴的方向建立极坐标系，并建立直角坐标系．

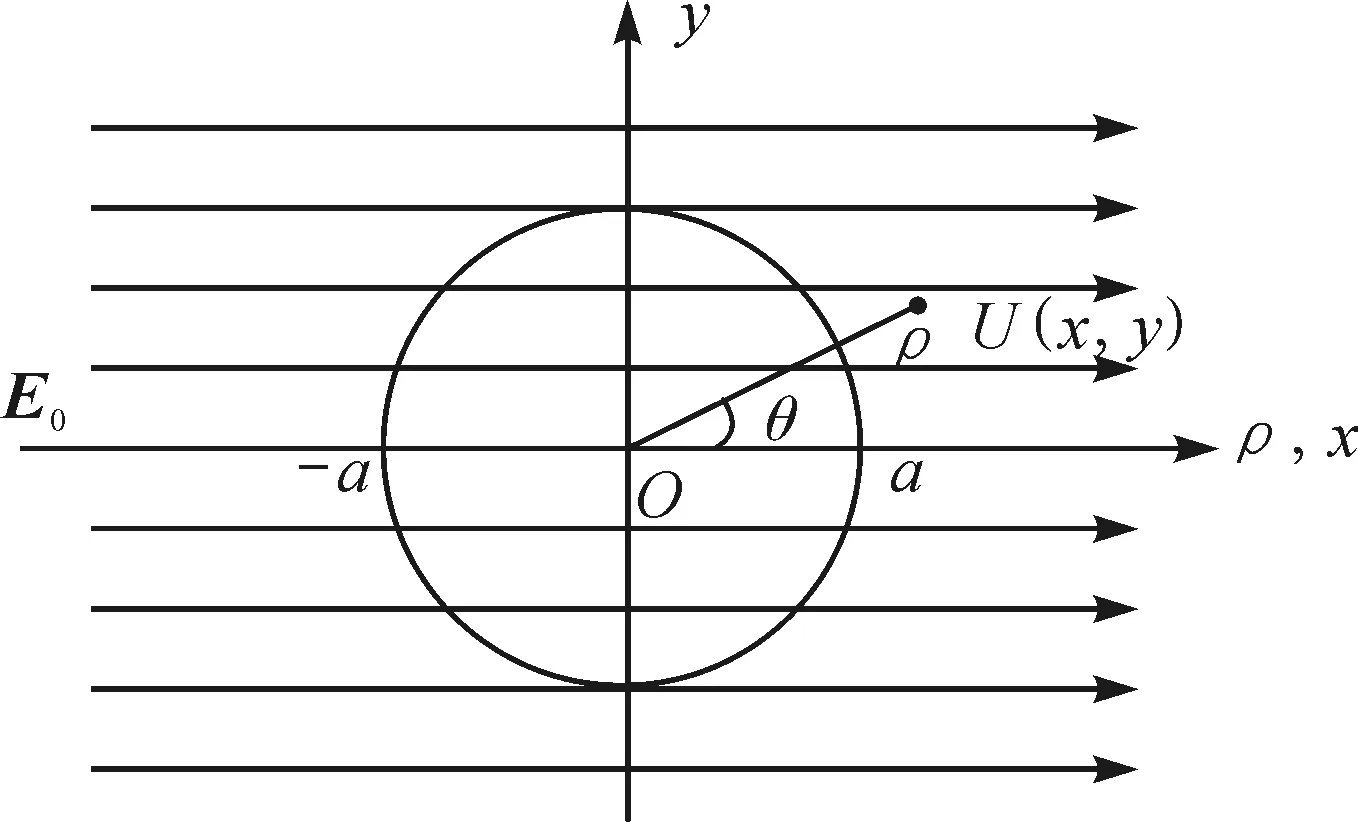
图1 单独的匀强电场和导体球的截面图

导体球内部的场强为零，球心电势取为零．球外没有自由电荷，电势满足拉普拉斯方程，其通解为[8]

(1)

U→-E0ρP(cosθ) = -E0ρcosθ

(2)

所以

a1= -E0an= 0 (n≠ 1)

(3)

在ρ=a的表面上有U= 0，所以

所以

b1= -a1a3=a3E0bn= 0 (n≠ 1)

(4)

球外的电势为

(5)

其中，第一项是外电场产生的电势，第二项是感应电荷产生的电势，等效于一个电偶极子产生的电势．由于x=ρcosθ，y=ρsinθ，所以电势可用直角坐标表示

(6)

其中，极径ρ是x和y的二元函数

(7)

当U取常数时，式(5)和(6)就是等势线方程．当式(5)和(6)不取第一项时，可得

(8)

当Up取常数时，上式就是感应电荷电场的等势线方程．

场强在直角坐标系中两个分量分别为

(9)

(10)

当y= 0时，可得轴线上的场强

(11)

当x= 0时，可得中垂线上的场强

(12)

合场强大小为

(13)

其方向与x轴正向夹角为

(14)

场强在极坐标系中的两个分量分别为

(15)

(16)

由于电场线的切线方向与场强的方向相同，二者的斜率相同，故可在极坐系中建立电场线的微分方程

(17)

分离变量得

即

积分可得

电场线在极坐标系中的隐函数方程为

(18)

其中c=eC．由于y=ρsinθ，所以电场线在直角坐标系中的隐函数方程为

(19)

(20)

3 公式的无量纲化

取a为坐标单位，E0为场强单位，则无量纲的场强分量分别为

(9*)

(10*)

(7*)

无量纲的合场强和方向分别为

(13*)

取U0=E0a为电势单位，则无量纲的电势为

(6*)

当电势U*为常数时，上式就是等势线方程．电场线的隐函数方程为

(19*)

常数由电场线的坐标决定．同理可以将感应电荷的等势线方程和电场线方程无量纲化．

4 电场的可视化

根据无量纲公式，利用MATLAB的指令即可设计程序，绘制电场强度的曲面以及电场线和等势线[4],程序见附录．当导体球放置在匀强电场中时，由于导体球的截面是圆，所以在柱坐标系中画电场强度的曲面比较理想，可以避免直角坐标系中的曲面在分界面上出现参差不齐的现象．应用等高线指令contour画等势线是一种常用的方法，用同一指令画电场线的方法则十分巧妙．

如图2所示，当导体球放到匀强电场中时，球内场强的x分量Ex为零，分界面上的Ex发生了跃变，球外场强分量Ex随着极角θ的增加而波浪形的变化，在上下外表面(0,±a±)处Ex最小，最小为零；在左右外表面(±a±,0)处Ex最大，最大为3E0；在距离ρ很大处，Ex→E0．图2的俯视图是一个彩色的圆面，网格线是圆和射线，极大值及其附近的颜色比较红，极小值及其附近(包括圆内部分)的颜色比较蓝．

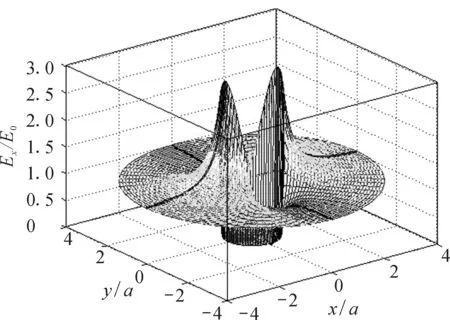
图2 导体球在匀强电场中场强的x分量

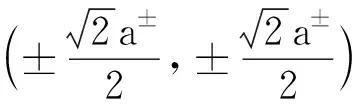
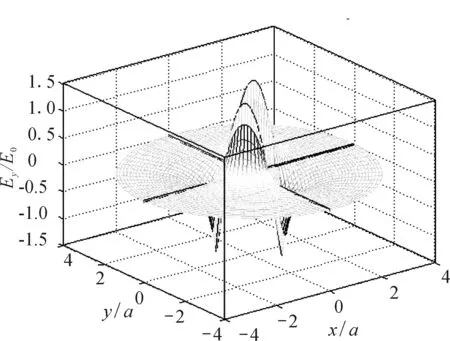
图3 导体球在匀强电场中场强的y分量

如图4所示，合场强E的曲面与Ex的曲面类似，这是因为Ex是场强的主要部分．

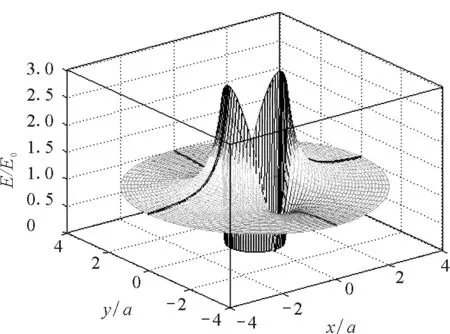
图4 导体球在匀强电场中的合场强

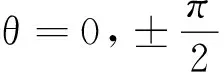
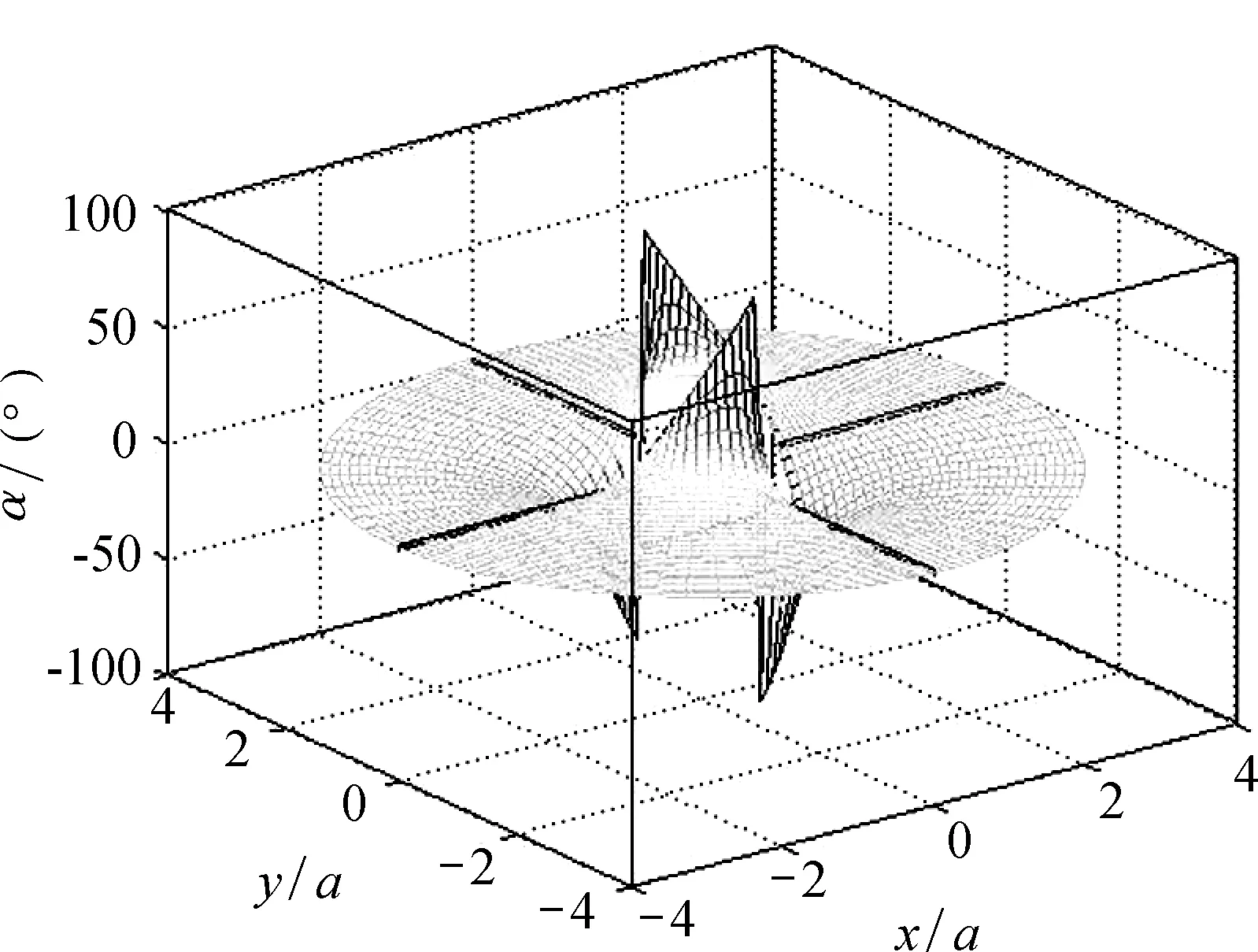
图5 导体球在匀强电场中合场强的方向

如图6所示，匀强电场的等势线本来是分布在一个与x轴有一定夹角的斜面上的平行线，放入导体球之后，该斜面变成带水平圆面的曲面，水平圆面表示导体是零势面，三维等势线分布在曲面上．除了U= 0的直线与圆面相交外，圆面附近的三维等势线都绕过了圆面；距离越远，等势线越直．

如图7所示，匀强电场中的导体球在右表面出现正电荷，在左表面出现负电荷，感应电荷在导体内产生匀强电场，与外电场抵消后使导体球内部的场强为零，导体球变成一个等势体．电场线从左边无穷远处发出，终止于导体球左表面上的负电荷；电场线从导体球右表面的正电荷发出，终止于右边的无穷远处．等势线是图6中三维等势线在Oxy平面上的投影，电场线与等势线正交．电场线和等势线在导体球上下外表面附近比较稀疏，说明这些地方的场强比较小；在导体球左右外表面附近比较密集，说明这些地方的场强比较大．

图6 导体球在匀强电场中的电势

图7 导体球在匀强电场中的电场线和等势线

如图8所示，如果不考虑外电场，感应电荷在导体内产生匀强电场，电场线的方向从右边指向左边；感应电荷在导体外的电场线从正电荷出发，终止于负电荷．感应电荷的电场与外电场E0叠加，其电场线和等势线如图7所示．

图8 导体球感应电荷的电场线和等势线

5 结束语

为了研究电场，根据物理定律建立数学模型是十分必要的．为了画图，通常需要将表达式无量纲化．场强曲面既可以在直角坐标系中绘制，也可以在柱坐标系中绘制，由具体问题决定．电场线一般用流线指令绘制，许多电场问题都可以推导出电场线的隐函数方程，用等高线指令画电场线是一种十分巧妙的方法．如果匀强电场中放置的不是球形导体，而是球形电介质，其电场也可以用完全相同的方法研究并绘制图形．曲面、等势线和电场线以及动画是描述电场的3种基本方法．

我们10年前出版了MATLAB与大学物理学相结合的教材，共有300多个各类程序，其中有40多个电磁学程序，相信对于读者具有一定的参考价值．如果有更多的高校师生将MATLAB与电磁学和电动力学结合起来，探索教学规律，将会进一步提高研究和教学水平．