奇特征有限域上的辛图

苏 磊 磊,南 基 洙,韦 扬 江

(1.大连理工大学 数学科学学院， 辽宁 大连 116024； 2.南宁师范大学 数学与统计学院， 广西 南宁 530001 )

0 引 言

在本文工作之前，研究者利用辛空间中的一维子空间和它们的正交性来定义辛图．Rotman研究了Z2上的辛图[1]．Tang等进一步对有限域上的辛图进行了探究[2]．利用组合的方法，Meemark等分别在Zpn、有限局部环和有限交换环上定义并研究了辛图[3-5]．利用矩阵的方法，Li等介绍了有限域上辛图的次成分[6]、Zpn上的辛图[7]，及Zpq上的辛图[8]．Gu研究了Zpn上辛图的次成分[9]．最近，Su等利用有限域上辛空间中的二维非迷向子空间和它们的交定义了一类新的辛图[10]．

1 Γ的性质

定义1图G中所有从顶点x到y的路的最短长度称为x到y的距离，记作dG(x，y)．

定义2[9]令图G是一个顶点数为v的k-正则图．若图G中的任意两个不同顶点之间有c1，c2，…，cd-1或者cd个公共邻接点，则称图G是一个参数为(v，k，{c1，c2，…，cd})的d-Deza图．特别地，2-Deza图即为通常的Deza图

引理1[11]辛图是顶点可迁的．特别地，Sp2ν(q)顶点可迁地作用在Γ上．

□

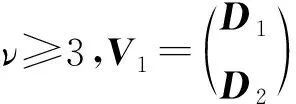
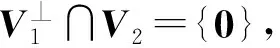
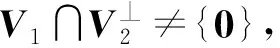
引理3[11]若ν=2，则Γ是一个参数为

的强正则图．

下面考虑ν≥3时的Γ的结构．

□

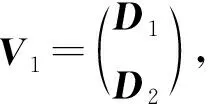
性质2令ν≥3．对于Γ中的任意两个相邻顶点V1和V2，有

□

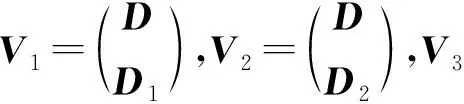
性质3令V1和V2为Γ中的任意两个不相邻顶点．

(1)若ν≥4，则|N(Γ，V1，V2)|=q+1，2q+1，(q+1)2．

(2)若ν=3，则|N(Γ，V1，V2)|=q+1，2q+1．

证明(1)令V3是V1和V2的公共邻接点．

□

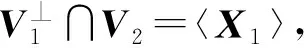
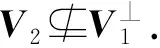
由性质1、2和3，有以下定理．

定理1(1)若ν=3，则Γ是一个参数为

的4-Deza图．

(2)若ν≥4，则Γ是一个参数为

的5-Deza图．

2 次成分Γ1

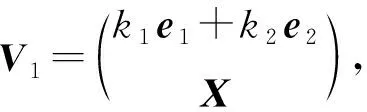
定理2若ν=2，则Γ1是一个参数为

(q(q+1)，q-1，q-2，0)

的强正则图．

证明由引理3可知，|V(Γ1)|=q(q+1)，且存在q-1个顶点与任意的V1∈Γ1相邻．

□

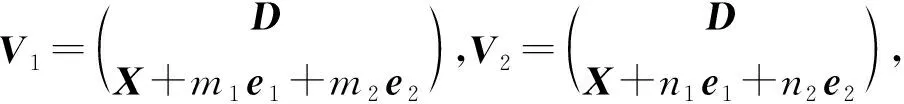
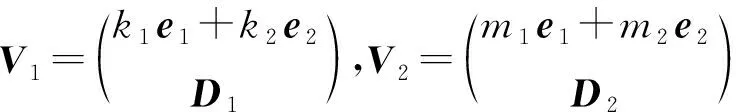
定理3若ν≥3，则Γ1不是正则图．

定理4令ν≥3，对于Γ1中的任意两个相邻顶点V1和V2，有

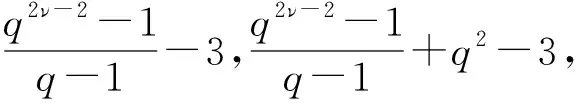
q2+q-2

证明令V1∩V2=〈D〉，V3是V1和V2的公共邻接点．

假设〈D〉V0，有其中若〈D〉⊆V3，则其中〈s1e1+s2e2〉≠〈k1e1+k2e2〉，〈s1e1+s2e2〉≠〈m1e1+m2e2〉．于是V3的个数为(q+1)-2=q-1．若〈D〉V3，则其中l≠0或n≠0．从而V3的个数为q2-1．

□

定理5令ν≥3，对于Γ1中的任意两个不相邻顶点V1和V2，有

|N(Γ1，V1，V2)|=2q，q，0

□

□

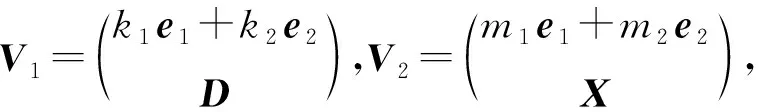
3 次成分Γ2

定理7若ν=2，则Γ2是一个参数为

(q3，q2-1，{q-2，q-1，q+1})

的3-Deza图．

□

引理4令V1是Γ2中的任意一个顶点．

证明(1)令V2与V1相邻．

□

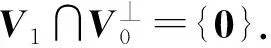
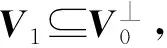
由引理4，有以下定理．

定理8若ν≥3，则Γ2不是正则图．

定理9令ν≥3，对于Γ2中的任意两个相邻顶点V1和V2，有

证明令V1∩V2=〈D〉，V3是V1和V2的公共邻接点．

假设〈D〉V3．因为〈D〉V0，所以D=H+k1e1+k2e2，其中有

□

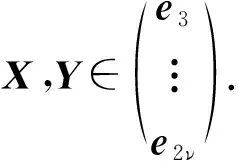
(1)若ν≥4，则|N(Γ2，V1，V2)|=q-1，q+1，2q，q(q+1)．

(2)若ν=3，则|N(Γ2，V1，V2)|=q-1，q+1，2q．

□

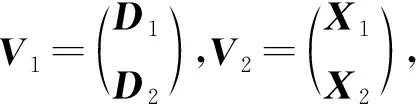
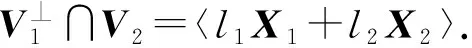
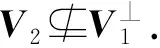
(1)若ν≥4，则|N(Γ2，V1，V2)|=q，q+1，2q，2q+1，q(q+2)．

(2)若ν=3，则|N(Γ2，V1，V2)|=q，q+1，2q，2q+1．

证明(1)令V3是V1和V2的公共邻接点．不失一般性，可以假设x3=0且y3≠0．为方便起见，记D1=H1+k1e1+k2e2，D2=H2+n1e1+n2e2，X1=x1H1+x2H2+s1e1+s2e2且X2=y1H1+y2H2+y3N+t1e1+t2e2．

□

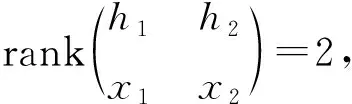
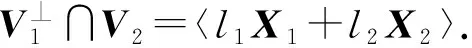
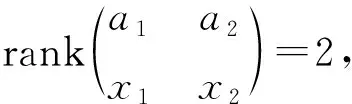
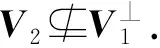
(1)若ν≥4，则|N(Γ2，V1，V2)|=q+1，2q+1，(q+1)2．

(2)若ν=3，则|N(Γ2，V1，V2)|=q+1，2q+1．

证明与性质3的证明方法类似可得．

□

由引理5、6和7，有以下定理．

定理10令V1、V2是Γ2中的任意两个不相邻顶点．

(1)若ν≥4，则|N(Γ2，V1，V2)|=q-1，q，q+1，2q，2q+1，q(q+1)，q(q+2)，(q+1)2．

(2)若ν=3，则|N(Γ2，V1，V2)|=q-1，q，q+1，2q，2q+1．

4 结 语