基于OpenSees的砂土本构模型对比研究

2022-01-26周林禄邱志坚凌贤长张安琪青岛理工大学土木工程学院山东青岛66033厦门大学建筑与土木工程学院福建厦门36005

地震工程学报 2022年1期

周林禄, 苏雷, 邱志坚, 凌贤长,3, 张安琪(. 青岛理工大学土木工程学院, 山东青岛 66033; .厦门大学建筑与土木工程学院, 福建厦门 36005;

3. 哈尔滨工业大学土木工程学院, 黑龙江哈尔滨 150090)

0 引言

砂土液化是造成地震灾害的重要原因之一,其机理是饱和砂土在循环荷载作用下有效应力逐渐减小,孔隙水压力逐渐上升,砂土由固态转变流动状态。在1964年Niigata地震和Alaska地震[1-2]、1976年唐山地震[3]、1989年San Francisco地震[4]、1995年Kobe地震[5]和2018年Palu地震[6]中,由饱和砂土液化引起的工程结构破坏造成了巨大的人员伤亡和财产损失。因此,研究饱和砂土液化问题对地震易发区的工程结构抗震具有重要意义。针对砂土液化特性,研究者开展了各种类型的室内和原位试验。如Adalier等[7]通过离心模型试验研究了超固结比(OCR)对饱和砂土液化的影响,发现随着OCR的增加,引起超孔压累积所需的加速度阈值将会增加。周燕国等[8]对含黏粒砂土进行了离心机振动台试验,发现含黏粒砂土与洁净砂之间渗透系数的差异性导致振动过程中二者超孔压的产生和消散速率显著不同。陈国兴等[9]开展了一系列循环三轴试验,研究饱和砂砾土的两种液化破坏机理:均等固结条件下的液化破坏和非均等固结条件下的轴向应变累积破坏。付海清等[10]基于现场液化试验研究饱和砂土的动力特性,试验结果表明相对密度对孔压累积速率能起到明显的控制作用。Chattaraj等[11]基于共振柱试验和循环三轴试验研究了砂土的动剪切模量和阻尼等特性,并建立了砂土最大动剪切模量和循环强度的关系。Dash等[12]研究了循环荷载频率对饱和砂土抗液化性的影响,发现随着循环加载频率的增加,超孔压累积速率也增加,即抗液化性随着加载频率的增加而降低。Moayed等[13]通过循环三轴试验,发现土工布在试样中的排列对砂土动力特性起主导作用,当土工布靠近试样顶部时砂土抗液化性能增加。Amini等[14]、Sonmezer[15]分别基于循环三轴试验和循环剪切试验,采用能量法分析了砂土的液化特性。Wang等[16]研究了不同波形的动荷载对砂土动力特性的影响。Yazarloo等[17]通过纳米技术对砂土进行不同程度的加固,分析其抗液化性。

综上所述,研究者在砂土液化领域做了很多室内和现场试验,但这些试验存在成本高和周期长等局限性,尤其是大型试验(如振动台或离心机试验)和参数分析。相比之下,在典型动力试验结果的基础上利用数值模拟标定现有的本构模型,进而进行参数分析,能够有效避免上述问题。如凌贤长等[18]针对非自由可液化场地大型振动台试验,采用有效应力原理和应力循环孔压增量计算方法建立数值计算模型,计算结果显示孔压比的增长与试验结果基本一致。周健等[19]采用二维颗粒流程序PFC2D分析了砂土振动液化时的宏观力学响应和细观组构演化。唐亮等[20]通过有效应力原理建立土体液化分析模型,并基于该模型建立自由液化场地振动台试验的有限元模型,通过试验值和计算值的对比验证了土体液化模型的可靠性。Zhang等[21]提出了预测饱和砂土液化后变形的理论框架,能够保证在有效应力消失时数值模拟的稳定性。Shahir等[22]通过引入渗透系数和超孔压比的关系对完全耦合的砂土动力学模型进行修正,结果表明修正后的模型能更准确地模拟砂土变形和孔压的累积过程。Wang等[23-24]针对饱和砂土进行了离散元数值模拟,发现砂土细观结构特征的变化会影响其抗液化性和液化后剪应变的发展,并建立了砂土细观结构变化和抗液化性的关系。魏星等[25]基于离散元的数值模拟方法,发现由循环剪切引起的孔隙均匀化和土颗粒间孔隙增大是液化后循环剪应变逐渐增大的细观原因。

目前已开发的用于模拟砂土液化的本构模型有很多,而对不同本构模型的合理选用是一个关键问题。王刚等[26]详细分析了不同本构模型模拟砂土液化变形的机制,并进行了不同模型响应对比。Ramirez等[27]利用两种数值计算方法,系统地比较了两个砂土本构模型(PDMY02模型和SANISAND模型)在地震荷载作用下土层的沉降、加速度和超孔压响应特性;通过对比离心机试验结果发现:两个本构模型均能够很好地预测土层的地震响应,但在模拟土体沉降方面仍需要改进。Sun等[28]基于修正的临界状态线发展了一种砂土边界面塑性本构模型,并与Li等[29]提出的模型进行了比较,结果表明边界面塑性本构模型能够再现砂土典型的应力-应变响应。

因此,为了尽可能准确地模拟地震荷载下饱和砂土的响应特性,基于开源地震工程模拟系统OpenSees,对其材料库中的4种典型砂土本构模型:PDMY(Pressure Depend Multi Yield)模型、Stress Density模型、Manzari Dafalias模型和CycLiqCPSP模型(砂土液化大变形统一本构模型)进行模拟测试,分析并对比每个模型的动力响应结果,以期为相关数值模拟提供参考和借鉴。

1 饱和砂土本构模型简介

1.1 PDMY模型

PDMY模型是由Yang等[30]提出的一种弹塑性饱和砂土液化本构模型,主要用于模拟循环荷载条件下对围压敏感的土体材料的非线性响应特性。模型屈服函数遵循经典的塑性约定。土体材料的弹性响应认为是线性和各向同性的,而塑性响应认为是非线性和各向异性的。在应力空间坐标系中,许多具有共同顶点和不同尺寸的相似屈服面形成了硬化区,每个屈服面都与一个塑性剪切模量值相关联,最外侧屈服面为破坏面。该模型采用偏分量相关联和体积分量非关联的流动规则,土体的剪胀和剪缩特性由非相关联流动法则控制。

1.2 Stress Density模型

Stress Density模型是由Cubrinovsk等[31]基于初始状态概念的框架构建的一种砂土应力-应变-剪胀模型。该模型基于孔隙比和法向应力状态相关联的思想建立,其应力-应变关系基于初始状态概念建立,通过定义状态指数变量来量化相对初始状态。模型采用连续屈服假设定义了塑性应变增量方向与应力增量方向的依赖关系。

1.3 Manzari Dafalias模型

Manzari Dafalias模型[32]是由应力比控制、同时考虑临界状态的饱和砂土塑性模型。该模型基于一般土体本构模型的特征,对模型结构的简单性与模型功能的复杂性进行了适当平衡。模型假定只有应力比的变化才能引起砂土塑形剪切变形和体积的变化,而在恒定的应力比下应力的增加仅由弹性应变引起,对于塑性应变则通过引入其他塑性加载机制来实现。模型采用剪胀张量模拟循环荷载下的剪胀和剪缩响应特性。

1.4 CycLiqCPSP模型

CycLiqCPSP模型是由Wang等[33]基于切割平面算法构建的一种饱和砂土液化本构模型,特别考虑了循环特性和液化后剪切大变形的累积。该模型基于物理方法计算零有效应力下剪切应变的累积,采用统一方法描述砂土液化前后的特性。模型基于剪胀引起的两个体积应变分量分析砂土在单调和循环荷载下的剪胀特性,同时假定由平均有效应力引起的体积应变为弹性,由剪切变形引起的体积应变为塑性。模型还引入了临界状态土力学概念,可以实现不同状态下砂土的统一建模。

2 数值模型途径

2.1 数值模型建立

为研究以上4种饱和砂土本构模型在相同荷载作用下响应的差异性,建立一个单元的二维饱和砂土流-固耦合测试模型(图1)。模型尺寸为1 m×1 m,采用OpenSees中的9_4_QuadUP单元。该单元基于Biot多孔介质理论,采用u-p公式的有限元形式(u表示土颗粒位移,p表示孔隙水压力)[34],考虑了土骨架和孔隙水之间的相互影响,用于模拟固-液两相完全耦合材料的动力响应。如图1所示,土单元的4个角节点各具有3个自由度,其中前两个自由度代表土颗粒位移,第3个自由度代表孔压自由度。另外5个节点具有2个自由度,仅代表土颗粒位移。

图1 二维饱和砂土流-固耦合模型Fig.1 Two-dimensional fluid-solid coupling model of saturated sand

单元建立过程中,首先对节点1、2、5在x和y方向施加固定约束,保证单元初始位移为0;对节点3、4施加孔压约束,定义单元上边界为水位线。其次分别对节点3、4、7和节点6、8、9施加相同位移约束,以保证模型在动荷载作用下维持纯剪切状态。最后在单元底部施加如图2所示的正弦加速度,加速度频率为1 Hz,幅值为0.2g,整个施加过程持续10 s。数值计算过程分成两步:第一步计算土体在自重状态下的静力响应,分别实施土单元的弹性和塑性计算;第二步计算施加加速度后单元的动力响应。

图2 基底输入加速度Fig.2 Base input acceleration

动力分析中,为单元和节点分配阻尼。在OpenSees中使用瑞利阻尼时,单元或节点的阻尼矩阵D被指定为刚度和质量比例阻尼矩阵的组合:

D=αM+βK

(1)

式中:M和K分别为质量矩阵和刚度矩阵;α和β分别为质量矩阵系数和刚度矩阵系数,在对不同本构模型进行计算时,α和β统一取值,分别设置为0和0.002。

2.2 模型输入参数确定

为了更好地对比不同砂土本构模型在相同荷载作用下响应的差异性,需要尽可能地保证定义的不同模型参数代表同一类砂土。因此,各个模型基准参数的选取参考了以往研究者对相似密度下中砂的模型标定结果[30-33,35]。

考虑到剪切模量是饱和砂土最重要的模型参数,需要确保在循环荷载作用下不同本构模型具有类似的剪切模量。PDMY模型的剪切模量利用剪应力-剪应变骨干曲线描述,基于指定的参考围压与该参考围压下得到的小应变剪切模量参考值,建立本构模型中剪切模量随平均有效应力的变化关系:

(2)

式中:Gr为参考剪切模量;p′r为参考有效围压;d为压力系数。

Stress Density模型的剪切模量基于Iwasaki等[36]的研究成果,在建立剪切模量与有效应力关系时考虑了粒度分布对剪切模量的影响:

(3)

式中:A为弹性剪切模量参数;pa为大气压(参考围压);ei为孔隙比;n为压力系数。

Manzari Dafalias模型和CycLiqCPSP模型则根据Richart等[37]定义的经验公式建立剪切模量表达式,同时还考虑了初始孔隙比对剪切模量的影响:

(4)

式中:G0为剪切模量参数。

为消除数值模拟过程中剪切模量对响应结果的影响,对式(2)～(4)中的相关参数进行修正。图3为修正后各本构模型剪切模量与平均有效应力的变化关系。由图3可知,在这4个模型中,剪切模量与平均有效应力的变化关系曲线基本重合。表1～4分别列出了4个本构模型的输入参数,表5为数值模型中所采用单元的相关计算参数。

图3 剪切模量与平均有效应力的变化关系Fig.3 Relationship between shear modulus and mean effective stress

参数数值密度ρ/(kg·m-3)1 900参考剪切模量Gr/kPa8.1×104参考体积模量Br/kPa2.0×105摩擦角φ/(°)33峰值剪应变γ0.1参考有效围压p′r/kPa101.3压力系数d0.5相位转换角φT/(°)27剪缩参数c0.07剪胀参数d1,d20.4,2液化参数l1, l2, l310,0.01,1

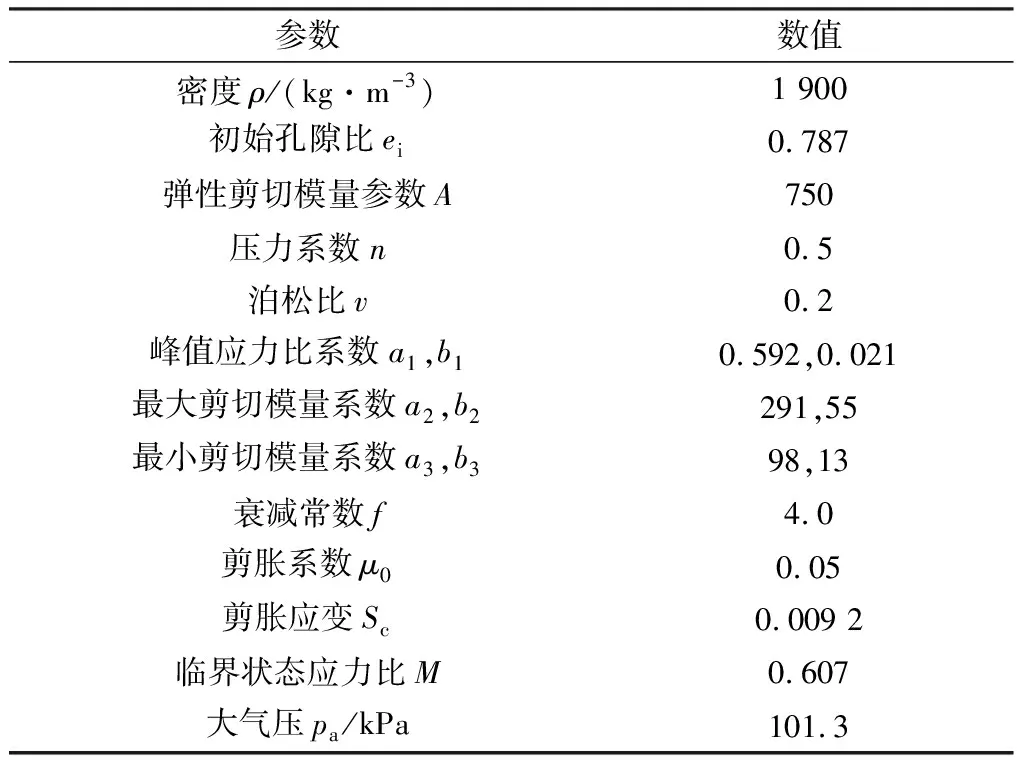
表2 Stress Density模型参数

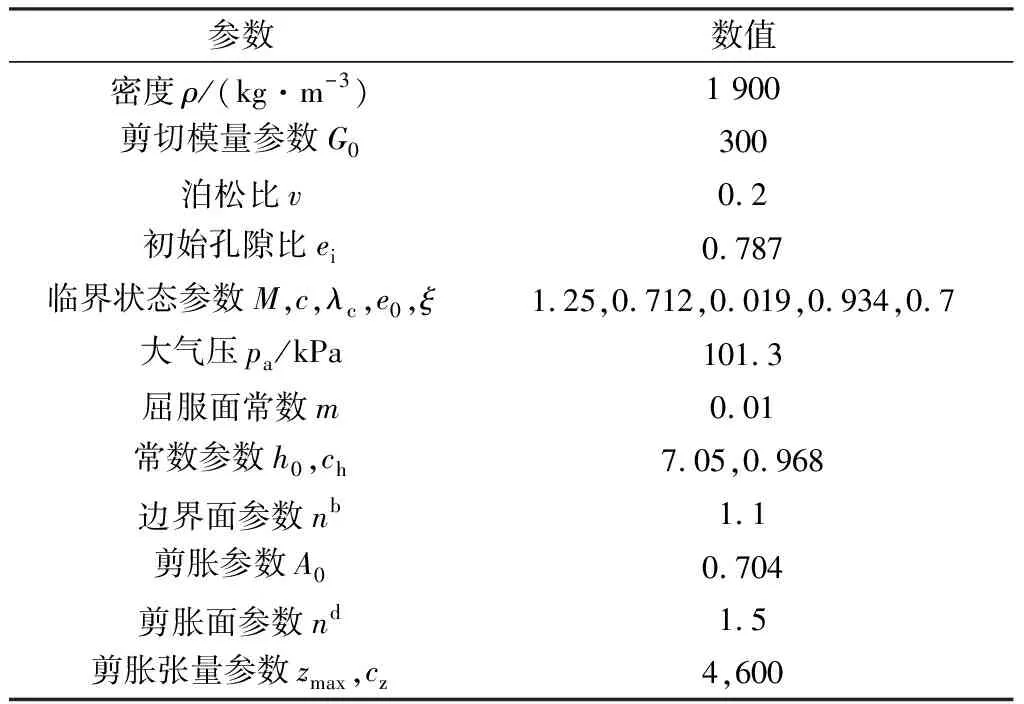
表3 Manzari Dafalias模型参数

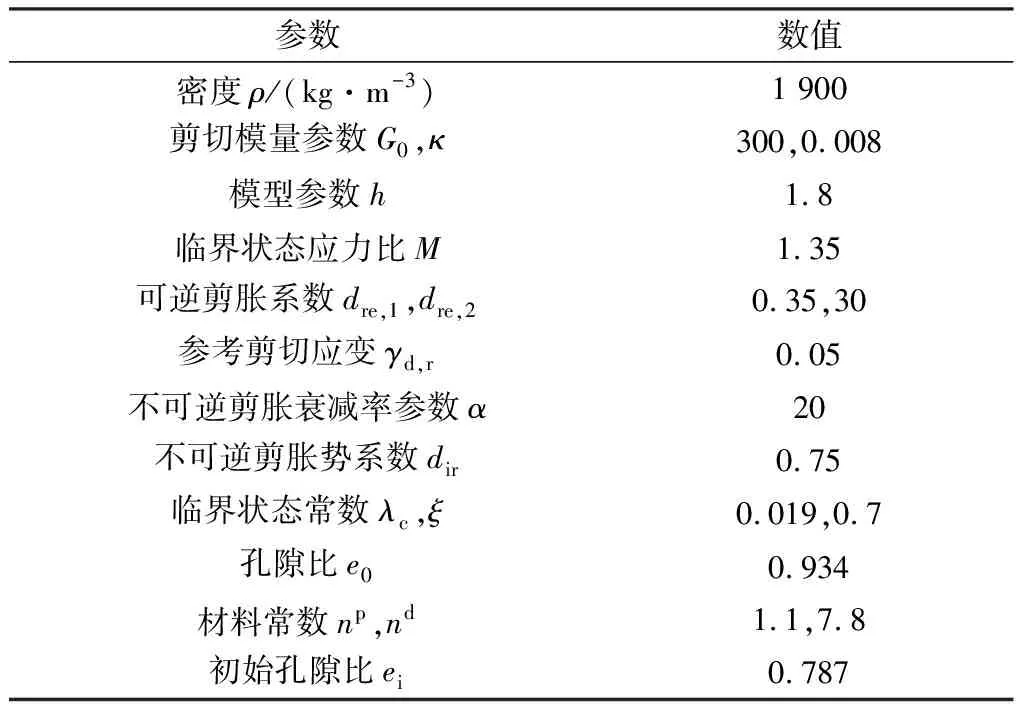
表4 CycLiqCPSP模型参数

表5 单元相关参数

3 计算结果分析

基于上述数值建模途径,采用OpenSees有限元模拟程序进行数值计算,得到不同饱和砂土本构模型的动力响应结果。下面将从加速度、超孔隙水压力、位移、剪应力-剪应变和平均有效应力路径响应方面进行分析,研究各本构模型的动力响应规律,对比不同模型响应的差异性。

3.1 加速度响应

图4给出了4种模型土单元节点3的水平加速度随时间变化关系。由图可知,PDMY和Cyc-LiqCPSP模型的节点加速度响应峰值和波形基本保持一致,与输入的加速度相比,波形改变的幅度较小。另外注意到,Stress Density模型和Manzari Dafalias模型从第2个循环开始,加速度表现出较明显的放大效应。对于不同模型,该放大效应的大小表现出一定的差别。

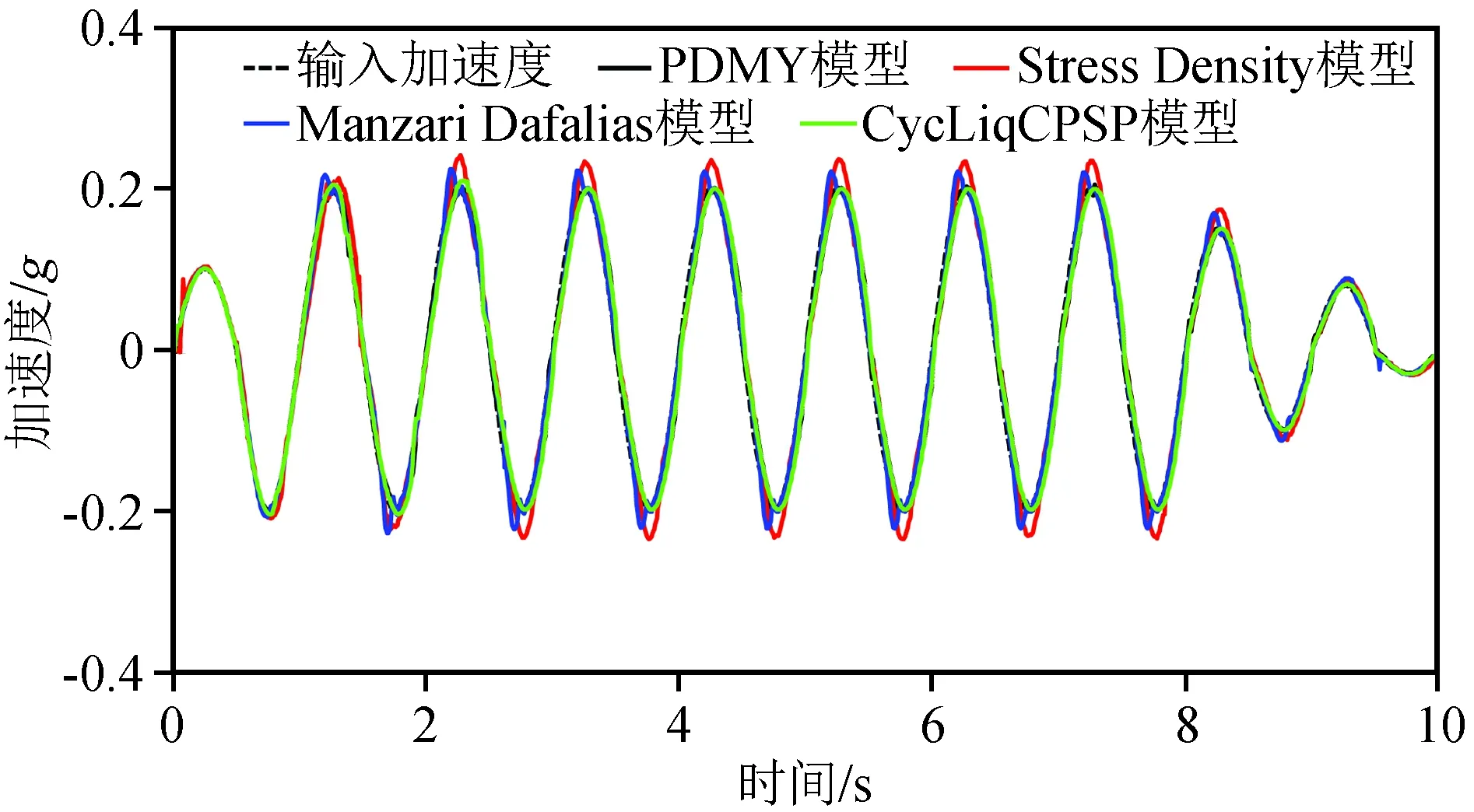
图4 不同砂土本构模型节点3加速度时程Fig.4 Acceleration time histories of Node 3 for different sand constitutive models

3.2 超孔压响应

图5给出了循环动力荷载作用下不同本构模型饱和砂土单元在节点1处的超孔压变化时程曲线。PDMY模型在起始阶段,随着加速度的施加超孔压逐渐增加,但增加的速率逐渐降低;在第6 s,超孔压增加到最大值,即达到初始有效应力,饱和砂土单元发生液化。Stress Density模型在加速度施加的第1 s出现了短暂的负超孔压,这是因为该模型材料在循环荷载作用下产生了较明显的剪胀和剪缩效果,即当加载时,砂土单元表现为加载膨胀,其内部孔隙在一瞬间发生扩张,从而导致孔隙水压力减小;当卸载时,砂土单元表现为卸载收缩,此时超孔压开始上升[38]。

另外由图5可知,超孔压波动频率比输入加速度的频率高,这与砂土在动荷载作用下的剪缩、剪胀交替变化有关。当剪应变增大时,孔压出现回降(加载剪胀),而当剪应变回退时,孔压又迅速上升(卸载剪缩)。由于每个完整的加速度周期有两个加载段(正负两个方向),所以超孔压波动的频率为输入加速度频率的2倍。不断交替的剪胀和剪缩作用造成了Stress Density模型土单元超孔压的急剧升高和降低,仅加载两个周期的循环时间,超孔压即在某些瞬间达到初始有效应力,砂土单元开始连续出现“瞬态液化”现象,且超孔压持续在比较大的范围内波动。Manzari Dafalias模型同样在加载两个周期的循环时间出现了连续的“瞬态液化”现象,但相比Stress Density模型,其剪胀特性稍弱。该模型响应的初始阶段未出现负超孔压现象,在液化后超孔压一直保持中等幅度的波动,持续到加载8 s左右,之后超孔压波动幅度变小。结合图4不难发现,剪胀特性越强,其加速度的响应峰值也越高。Cyc-LiqCPSP模型在循环正弦荷载作用下,超孔压先是呈稳定的小幅值增长,随后在第2 s增长到最大值,发生完全液化,紧接着发生剪胀作用,之后超孔压保持最大值且呈直线发展。

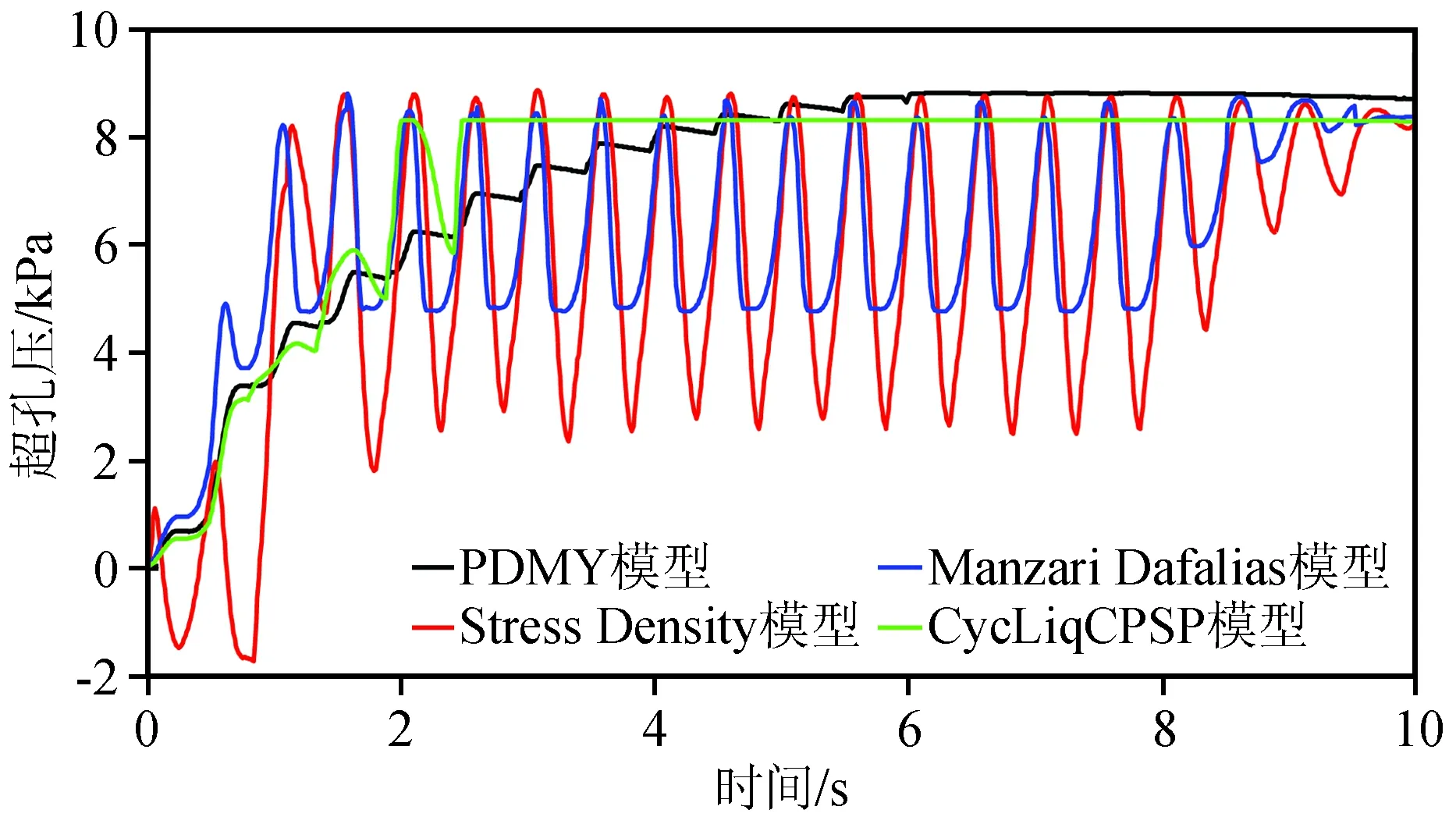
图5 节点1超孔压响应Fig.5 Excess pore pressure response of Node 1

3.3 位移响应

在加速度施加过程中,记录了土单元每个节点的位移响应。图6对比了不同本构模型在节点3的水平位移。由图可知,PDMY模型在0～6 s时间段内,位移响应幅值呈逐渐增加的趋势;在6～8 s,位移响应幅值开始保持稳定状态;在8 s之后,由于输入加速度幅值下降,位移呈减小趋势。Stress Density模型的位移时程响应显示,该模型在第1个加速度循环即产生较大的位移变化,之后位移向反方向发展,并在此基础上进行波动。这说明该土单元发生了永久变形,即该模型在循环荷载下更容易呈现永久变形的特性。结合图5可知,在永久变形发生时,超孔压刚好达到初始有效应力(即液化),因此这种永久变形是由土体液化引起的。Manzari Dafalias模型在第2个加速度循环达到最大位移,但位移幅值较小,之后幅值近似维持着恒定值,直到循环荷载结束。CycLiqCPSP模型的位移时程与PDMY模型相似,位移幅值在起始时段逐渐增加至稳定状态,但CycLiqCPSP模型更早到达最大位移响应幅值。这4种模型中,Stress Density模型由液化产生的累计变形最为显著,其他3种模型最终产生的累计变形很小,这与动荷载强度、加载时间以及单元尺寸等因素有关。

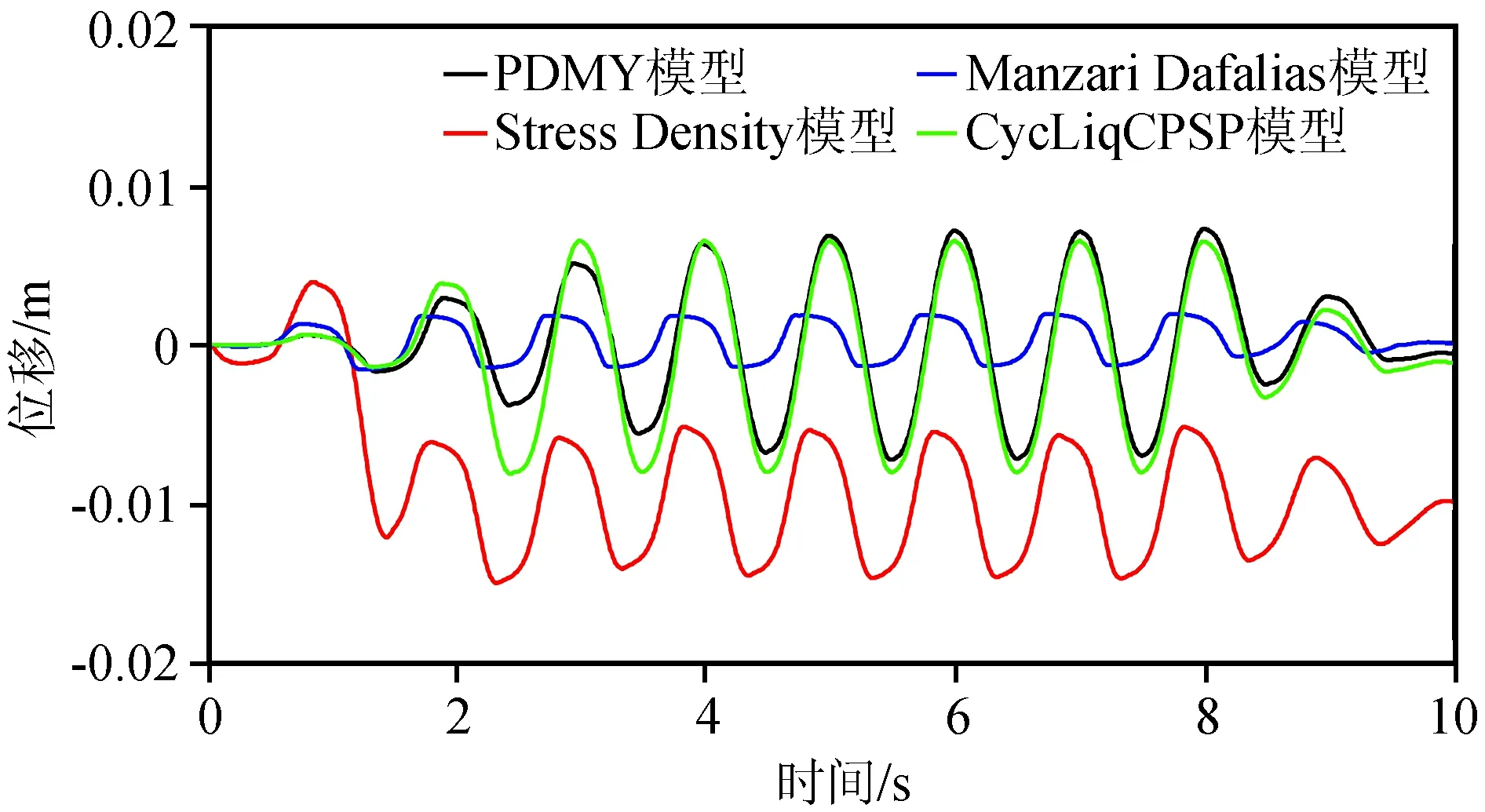
图6 节点3位移响应Fig.6 Displacement response of Node 3

3.4 剪应力-剪应变响应

图7给出不同本构模型在循环荷载作用下的剪应力-剪应变响应。从图7可知,PDMY模型随加速度循环次数的增加,土单元剪应力逐渐减小,剪应变逐渐增大。当节点位移和超孔压增长到最大值时,单元剪应力相应地减小到最小值,剪应变增长到最大值。值得注意的是,该模型的剪应力-剪应变响应呈阶梯状变化,即剪应力和剪应变分别以阶梯的形式逐渐减小和增大。Stress Density模型在加载的第2个周期内产生了较大的应变变化,此后滞回曲线一直停留在变化后的位置。这与位移响应结果相符合,说明该模型在动荷载作用下出现了累积永久变形。Manzari Dafalias模型在循环荷载作用下,其剪应力-剪应变响应始终稳定在一个大致范围内。显而易见,该模型的剪应变响应值较其他模型要小很多,这也是造成其位移响应值较小的直接原因。CycLiqCPSP模型随着加速度的施加,土单元剪应力减小的同时剪应变也在增大;与此同时,剪切刚度随着加速度循环次数的增加逐渐降低。当超孔压增长到最大值时土单元发生液化,此时剪切刚度降为0。对比该模型与PDMY模型不难发现,液化发生后两个模型的剪应力-剪应变滞回曲线几乎重合。

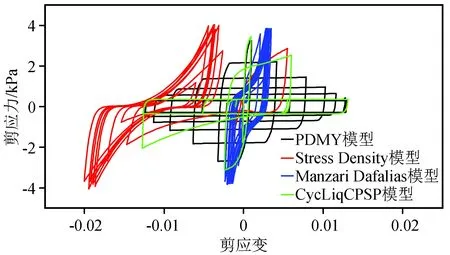
图7 土单元剪应力-剪应变响应Fig.7 Shear stress-strain response of soil element

3.5 平均有效应力路径响应

图8给出了砂土单元平均有效应力路径响应。由图8可知,PDMY模型随着动力循环荷载的施加,超孔压不断累积,从而导致平均有效应力不断降低,直至降为0。砂土单元的强度不断减小,位移幅值逐渐增大,最终达到完全液化状态时,土体完全丧失强度,此时节点位移增加到最大值。Stress Density模型在初始阶段,由于负超孔压的出现,平均有效应力有所增长;在之后的动荷载循环中,平均有效应力先是迅速衰减到最小值,随后立刻恢复,连续在其强度包线内进行大范围的波动。这与超孔压和单元剪应力的响应结果一致,都是由其剪胀特性所引起。Manzari Dafalias模型在第2个加载循环内,平均有效应力降到最小值,随后在其强度包线内波动,但波动的范围明显要小于Stress Density模型。CycLiqCPSP模型随着循环荷载的施加,由于超孔压的逐渐累积,其平均有效应力逐渐减小,在材料开始液化时,有效应力降低到最小值。需要注意的是,Manzari Dafalias模型和CycLiqCPSP模型的平均有效应力并没有精确衰减到0点,这是因为材料在达到液化后尚存在残余强度。