改进变分模态分解-多尺度排列熵结合广义回归神经网络的高压直流输电线路故障辨识

刘维，刘辉

(湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，武汉 430068)

直流输电技术因其远距离输电能力强、线路损耗低、节省资源等特点越来越大规模地应用到远距离输电领域中，但由于远距离输电架设线路的地域环境十分复杂，运行环境恶劣，因此发生故障的概率相对更高[1-2]。为了消除故障带来的影响，维持输电系统的稳定运行，需要一种高效可靠的保护方法确保故障能准确地切除，而保护的前提就是准确有效地辨识输电线路各种类型的故障。

为了解决上述问题，中外学者做了大量的研究以准确识别故障，研究方法以根据故障时电气量的差异性进行故障辨识为主，人工智能方法应用较少，前者普遍存在阈值难以确定、计算复杂等问题，后者则对故障特征提取有较高的要求，特征提取的效果直接影响故障识别准确率。文献[3]利用多分辨奇异谱熵和支持向量机识别特高压直流输电线路故障，该方法未考虑极间耦合效应的影响提取故障极特征，具有一定的局限性。

文献[4]提出基于改进方向电流法准确识别特高压直流输电线路故障，且能做到识别故障极，但阈值难以确定。文献[5]利用单端特征频率电流构造直流线路故障判别方法，能准确区分区内外故障并实现故障选极，但未分析低阻故障对识别效果的影响，耐受过渡电阻能力需进一步分析。文献[6]利用单环定理和广义S变换分别实现区内外故障和故障极的判别，故障识别率高，抗干扰能力强。

文献[7]利用交叉重叠差分(sequential overlapping derivative，SOD)变换对故障电压行波进行处理得到区内外故障识别准则，可以准确识别远端高阻故障。文献[8]提出基于暂态能量比的先导保护方法，利用线路边界的阻抗-频率特性进行内外故障的判别，但计算复杂。

通过以上分析可知，目前高压直流(high voltage direct current,HVDC)输电线路故障识别方法大多存在无法同时识别低阻和高阻故障等问题，且特征提取效果和故障识别率有待进一步提高。因此，现提出一种改进变分模态分解(variational mode decomposition,VMD)-多尺度排列熵(multi-scale permutation entropy,MPE)-广义回归神经网络(general regression neural network,GRNN)故障辨识方法，利用改进VMD-MPE提取故障电流信号特征扩大差异后构造故障特征向量，然后使用GRNN网络对各种类型故障进行辨识，从而达到准确识别区内外故障，且能同时识别低阻和高阻故障的目的。

1 信号分解与特征提取算法

1.1 变分模态分解

VMD能够分解故障信息，且可以有效地避免模态混叠现象，有利于分析故障信息从而有助于实现后续方法对故障信号的特征提取。VMD通过构造变分问题并求解变分问题实现对信号的自适应分解，将信号分解后可得到不同频带下的本征模态函数(intrinsic mode function,IMF)[9-10]。需构造变分模型为

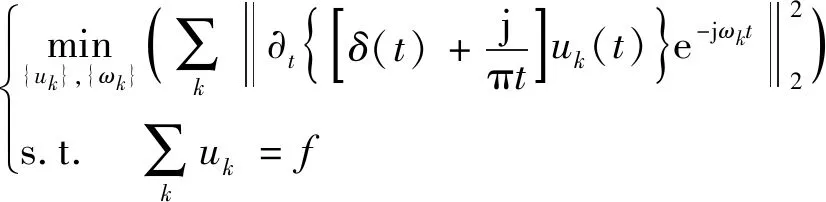
(1)

式(1)中：{uk}={u1,u2,…,uk}为不同频率的IMF分量；{ωk}={ω1,ω2,…,ωk}为不同分量的中心频率；f为故障电流信号；δ(t)为冲击函数。

引入二次惩罚因子α和拉格朗日乘法算子λ代入式(1)中以求出上述问题的最优解，得到非约束条件下的表达式为

L({uk},{ωk},λ)

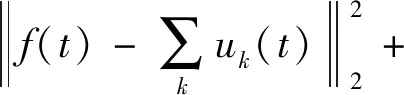
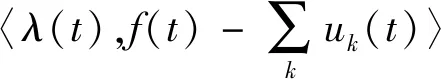
(2)

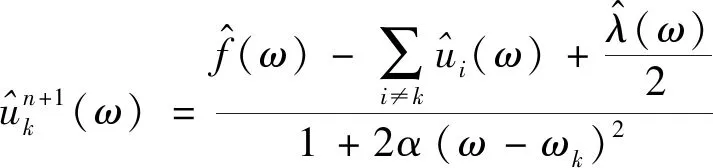
(3)

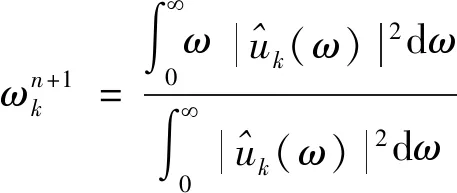
(4)

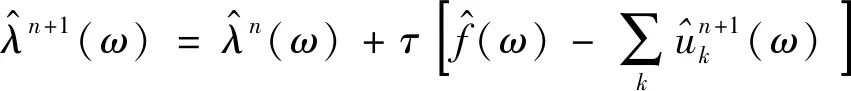
(5)

将上述过程中所得表达式的“鞍点”作为变分模型的最优解，即实现了故障信号f的VMD分解。

1.2 鲸鱼算法改进VMD方法

由于VMD算法分解故障信号时需要预设分解个数K，且设置K的大小不同，最终的分解效果也存在较大的差异，若K过小则可能出现模态混叠现象；若K过大则可能出现过分解现象，以及二次惩罚因子α的大小对VMD分解的模态分量的带宽有较大的影响[11]，因此，提出利用鲸鱼算法对分解个数K和二次惩罚因子α进行优化，求出算例中最优的K和α，以此提高VMD的分解效果。

利用鲸鱼算法对参数进行寻优时，需要确定适应度函数来评价寻优结果是否为最优。利用样本熵值评价寻优结果是否最优，样本熵值越小，表示分解后的序列产生新模式的概率越小，即序列中频率分量越少，故其模态混叠的可能性越小，分解效果相对会更好，因此计算每次分解后各IMF分量的样本熵值，将求解所有IMF样本熵中最小熵值的函数作为适应度函数。鲸鱼算法改进VMD的具体步骤如下。

步骤一参数初始化，设置最大迭代次数等参数。

步骤二种群初始化，将分解个数K和二次惩罚因子α组合作为不同鲸鱼的位置，并随机产生一定数量的参数组合(K,α)。

步骤三种群评估，根据不同参数组合对故障信号进行VMD分解，并计算每个IMF分量的样本熵值。

步骤四判断某一参数组合是否优于当前最优解，若是，则输出结果；若不是，则返回步骤三继续迭代搜索，直至得到最优参数组合。

1.3 多尺度排列熵算法

排列熵用于衡量时间序列的复杂程度，不同时间序列所对应排列熵值大小不同，越复杂的时间序列，其排列熵值越大；越规则的时间序列，其排列熵值越小[12-13]。由于不同类型故障的电流信号谐波含量不一样，使得其复杂程度存在较大差异，因此可通过计算故障电流信号的排列熵实现故障信号特征提取。与排列熵相比，多尺度排列熵可以从不同的时间尺度上度量时间序列的复杂程度，能够克服单一尺度排列熵度量时间序列存在的特征单一的问题[14]，计算多尺度排列熵的步骤如下。

步骤一将分解后得到的IMF分量进行s尺度的粗粒化处理，得到s尺度下的新的时间序列，公式为

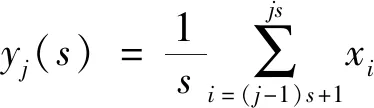
(6)

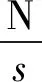
步骤二对粗粒化处理后的新时间序列进行嵌入维数为m和延迟时间为t的相空间重构，将各子序列X(i)内部进行递增排列，此时，每一个m维的子序列X(i)都被映射到m!个排列中的一个。

步骤三通过上述步骤就将一个m维的子空间表示成了一个符号序列，将所有符号的概率分布用P1,P2,…,PK表示，其中K≤m!。在不同的时间尺度下计算每组序列出现的概率，即可得到每个IMF分量的多尺度排列熵表达式为

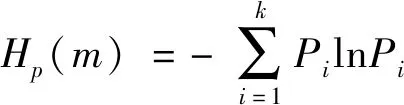
(7)

当Pi=1/m!时，Hp(m)取最大值ln(m!)。将Hp(m)归一化得

Hp(m)=Hp(m)/ln(m!)

(8)

式(8)中：0≤Hp(m)≤1，反映时间序列的随机程度，随机程度随着熵值的增大而变强。

2 改进VMD-MPE的HVDC输电线路故障特征提取

2.1 双极HVDC输电系统模型

双极HVDC输电系统由交流系统、换流站、交流滤波器、平波电抗器、直流滤波器和直流输电线路组成，其系统模型如图1所示。

图1中平波电抗器和直流滤波器构成了直流线路物理边界，该物理边界对高频分量和600、1 200、1 800 Hz特征频率具有阻隔和滤除作用，使得区内外故障信号存在较大差异[5]，因此可利用这一特性实现区内外故障类型的判别，且由于600 Hz信号频率相对较小，谐波含量相对较多，所以在对故障信号分解后选择频率接近600 Hz的IMF分量构造特征向量。

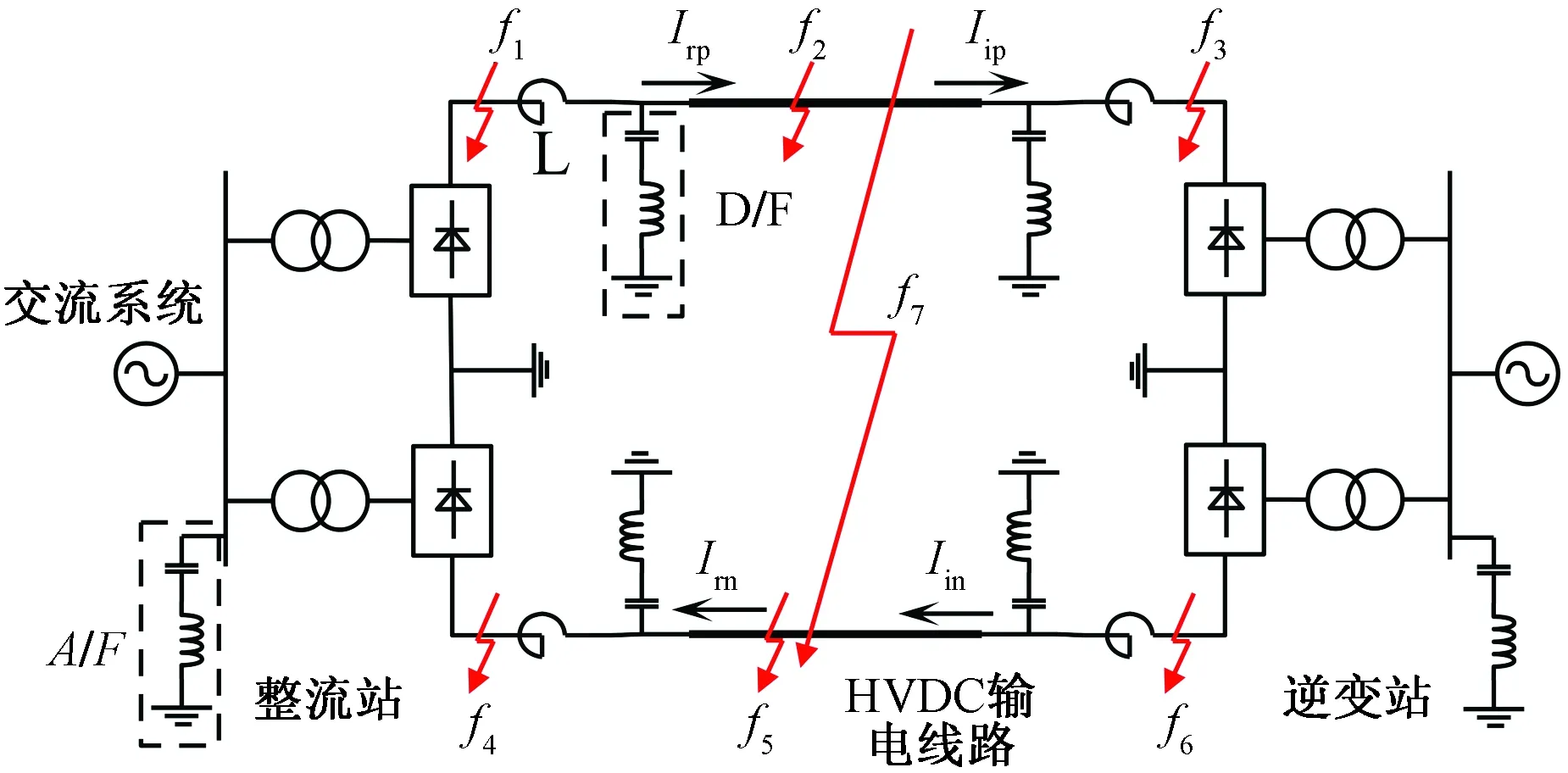
f1～ f7为不同类型故障点；f1和f4分别为整流侧区外正负极故障；f2和f5分别为区内正负极故障；f3和f6分别为逆变侧区外正负极故障；f7为双极短路故障；L为平波电抗器；D/F为直流滤波器；A/F为交流滤波器；Irp、Irn和Iip、Iin分别为整流侧正、负极电流和逆变侧正、负极电流图1 双极HVDC输电系统Fig.1 Bipolar HVDC transmission system

2.2 改进VMD-MPE故障类型特征提取

利用故障电流信号的线模电流分量进行改进VMD分解，之所以选择线模电流分量进行分解，是因为无论是正极还是负极发生故障，线模电流分量都能流过测量点被采集。对区内外正负极故障电流信号线模分量进行改进VMD分解，得到不同的IMF分量并计算多尺度排列熵，利用排列熵值组成故障类型特征向量。根据不同故障样本分别利用鲸鱼算法对VMD进行优化，得到不同故障样本下的最优(K,α)参数组合以及根据对应组合分解后选择的IMF分量部分最优参数组合及对应所选IMF如表1所示。

由表1可知，不同样本的最优参数组合不同，对信号分解后，选择对应的中心频率接近600 Hz的IMF分量进行特征提取，根据2.1节分析利用IMF分量计算多尺度排列熵构造故障类型特征向量。对区内和区外故障分别进行改进VMD分解和计算多尺度排列熵，区内故障以区内正极故障为例，故障距离50 km、故障电阻100 Ω，区外故障以整流侧区外故障为例，故障电阻100 Ω，分解结果如图2所示。根据1.2节分析可知，区内故障对应的排列熵值较大，区外故障对应的排列熵值较小，因此可以利用排列熵提取故障类型特征，结果如图3所示。

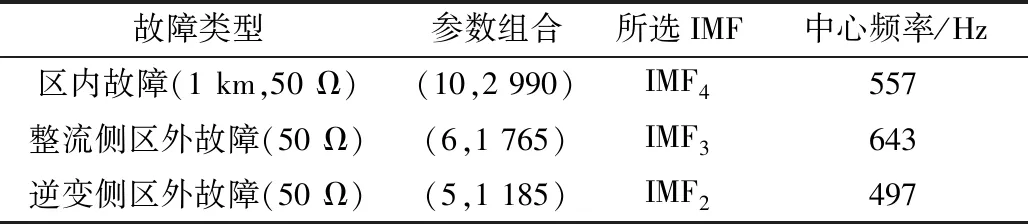
表1 部分最优参数组合及对应所选IMFTable 1 Part of the optimal parameter combination and corresponding selected IMF

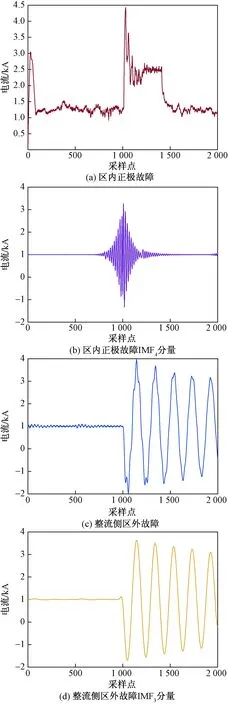
图2 不同类型故障及其IMF分量波形Fig.2 Different types of faults and their IMF component waveforms

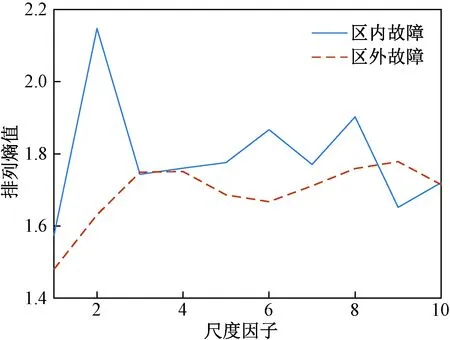
图3 不同尺度排列熵值对比Fig.3 Comparison of MPE in different scales

从图2可以看出，区内故障电流波形中谐波分量较多，波形较为复杂；区外故障电流波形中谐波分量较少，波形相对简单，且区内与区外故障的IMF分量的波形具有相同的规律。

由图3可知，在不同尺度下区内故障对应的排列熵值总体大于区外故障对应的排列熵值，基本符合1.2节中所分析的内容，且在尺度因子为2时，区内与区外故障对应的排列熵值差异最大，说明此时两个特征之间的区别明显，在该尺度下更容易区分不同类型的故障，因此尺度因子确定为2，计算多尺度排列熵，将不同类型故障的2尺度排列熵组成特征向量F=(F1,F2,…,Fn)1×n，用于提取故障类型特征。

2.3 故障极特征提取

双极直流输电系统发生故障时，由于两极之间存在电磁耦合效应，当某一极发生故障，健全极也会感应产生一定的电流突变量，可能会引起误判断[15]，影响故障辨识的效果。为了消除电磁耦合效应带来的影响，则需要准确地识别故障发生在哪一极。对于故障极的识别，引入IMF能量的概念，其定义为

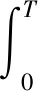
(9)

式(9)中：I(t)为故障电流函数；T为时间。

对式(9)做离散化处理得

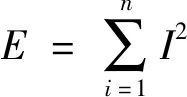
(10)

式(10)中：i=1,2,…,n为采样点；I为采样点对应的电流值。

由于健全极感应产生的电流突变量相对较小，其幅值相对于故障极电流突变量小，根据式(10)可知，故障极电流信号的IMF分量能量大于健全极IMF分量能量，因此可利用此特点识别故障极。计算改进VMD分解后得到的每个IMF分量的能量并求和作为IMF能量和，分别计算故障时正负极电流信号的IMF能量和，正极IMF能量和记为EP，负极IMF能量和记为EN，将EP与EN的比值作为故障判据Z，判别式为

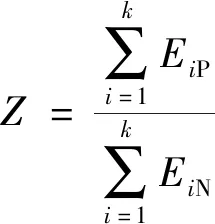
(11)

式(11)中：i=1,2,…,k为第i个IMF分量。

根据式(11)和上述分析可知，当Z>1时，故障极为正极；当Z<1时，故障极为负极。将发生不同类型故障时的IMF能量和组合作为故障极特征向量Z=(Z1,Z2,…,Zm)1×m，以此提取故障极特征，进而识别故障极。

3 GRNN故障辨识模型

HVDC输电线路故障辨识问题的求解目标是通过故障电流信号辨识出不同的故障类型，将提取的故障类型特征和故障极特征分别输入到两个GRNN故障辨识模型中进行故障辨识。GRNN故障辨识模型结构如图4所示，由于两个模型结构一致，因此仅给出一个模型结构图。

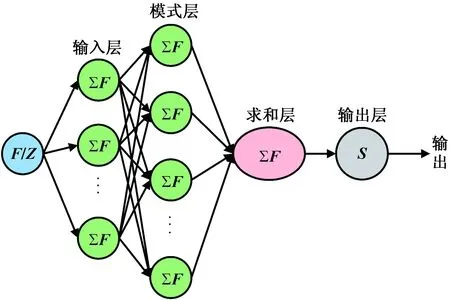
图4 GRNN 故障辨识模型结构Fig.4 GRNN fault identification model structure

GRNN属于径向基神经网络，其具有很强的非线性映射能力，而且学习速度很快，在处理小样本数据和精度较差的数据方面具有很大的优势。图4中：两个模型的输入分别为故障类型特征向量F和故障极特征向量Z，将两类输入分别导入两个GRNN模型中，经输入层直接传递到模式层，输入层样本数目为特征向量的维数；模式层与输入层全连接，以径向基函数为传递函数；求和层采用两种方式对模式层进行求和，一类是模式层的每个节点求算术和，另一类是每个节点求加权和；输出层输出的结果是模式层中所求的加权和除以算术和[16]，GRNN故障辨识模型的输出结果为列向量。

GRNN作为一种监督学习方法，在对不同类型输入进行训练识别时，训练样本需要包含标签信息，因此需要定义不同类型的输入变量的标签信息，文中对不同类型故障及故障极的标签信息定义如表2所示。

表2 GRNN辨识模型标签定义Table 2 GRNN identification model label definition

利用表2中所定义的标签信息结合前文所述提取的故障类型和故障极特征向量分别进行故障类型与故障极的识别，从而辨识出最终的故障类型。对区内正极故障、区内负极故障、整流侧区外正极故障、整流侧区外负极故障、逆变侧区外正极故障和逆变侧区外负极故障6种类型故障进行辨识。

利用GRNN故障辨识模型识别故障时包含训练和测试两个部分，首先，对输入的特征向量和对应的标签进行训练，经过训练之后，得到良好的训练模型；其次，将测试数据输入到此模型中，根据输出标签的结果便可判定辨识效果，将输出结果的准确率作为辨识效果的依据。

4 仿真验证

4.1 模型搭建与数据采样

为了验证所提出故障辨识方法的有效性，在PSCAD/EMTDC软件中搭建图1所示的双极HVDC输电系统模型并进行仿真分析。此模型送电电源功率为5 000 MVA，额定电压500 kV，频率50 Hz，输电线路全长800 km，直流滤波器使用2个双调谐滤波器搭建成1个12/24/36三调谐滤波器，设置故障起始时间为0.25 s，仿真总的时长为0.5 s。

区内故障设置故障距离为1、50、120、210、320、450、600、750和799 km共9种情况，设置故障电阻为1、50、100、200、300、400、500、600和650 Ω共9种情况，则区内故障共有2×9×9=162种情况，区外故障共有4×9=36种情况，区内和区外故障总共198类。对区内和区外故障分别进行采样构成样本集，采样频率4 kHz，然后利用此样本集数据进行仿真试验。

4.2 改进VMD方法性能分析

分别利用改进VMD和经验模态分解(empirical mode decomposition，EMD)方法对故障电流信号进行分解，然后对分解得到的前5个IMF分量进行快速傅里叶变换得到其对应的频谱图如图5和图6所示。

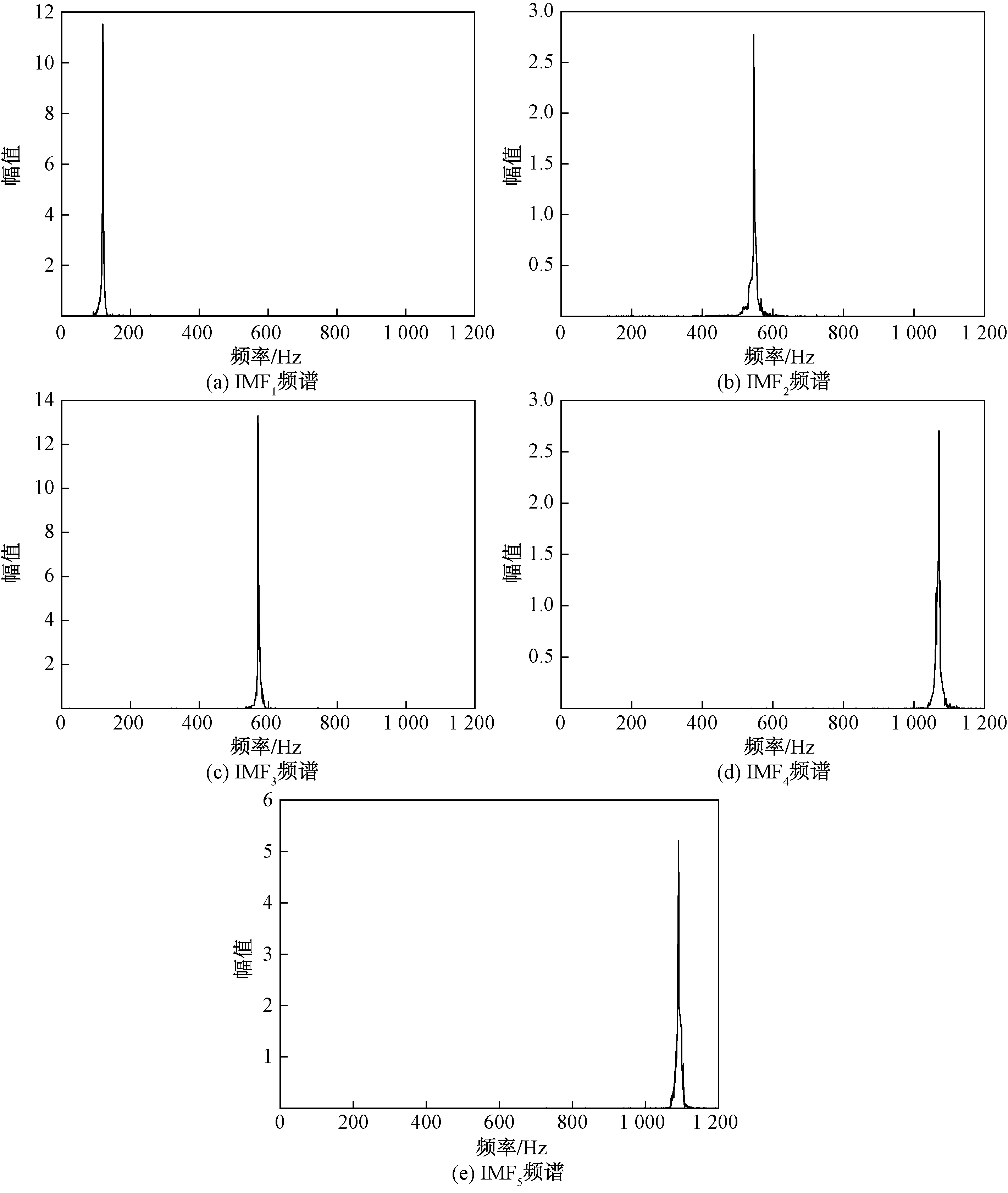
图5 改进VMD分解频谱图Fig.5 Improved VMD decomposition spectrogram

由图5和图6可以得出，改进VMD分解后的5个IMF分量仅包含单一频率的模态，未发生模态混叠现象；EMD分解后的第4个IMF分量包含389 Hz和435 Hz频率的模态，第5个分量包含332 Hz和379 Hz等多个频率的模态，发生了模态混叠现象，这表明改进VMD分解方法分解效果更好，避免了模态混叠现象，分解性能突出。

图6 EMD分解频谱图Fig.6 EMD decomposition spectrogram

4.3 改进VMD-MPE-GRNN方法性能分析

为了验证改进VMD-MPE-GRNN故障辨识方法对区内和区外故障辨识的优异性能，分别对6种故障进行数据采样，总共采样90组数据，每组数据包含11个样本，其中，设置70组数据为训练集，20组数据为测试集，训练集与测试集都随机选取。利用改进VMD-MPE方法对90组数据分别进行故障类型和故障极特征提取，将提取特征后的特征向量输入到GRNN故障辨识模型中分别进行区内外故障类型和故障极辨识，故障类型与故障极的辨识结果如图7和图8所示。

从图7和图8可以看出所提出的方法能够准确地辨识出区内外故障类型和故障极，总体准确率可达98.64%，不受故障类型的影响，在小样本故障辨识方面该方法的辨识性能优异。

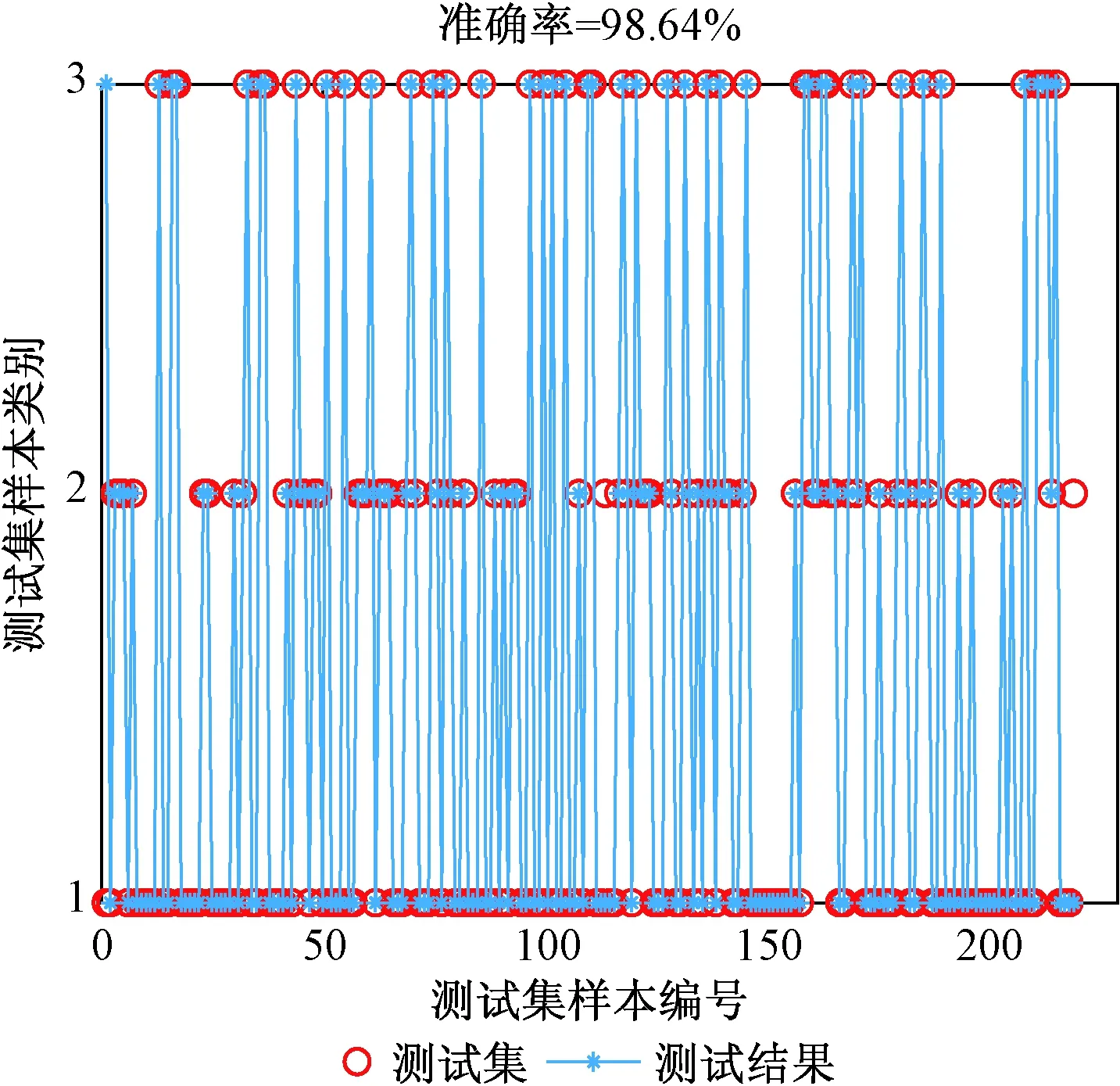
图7 区内外故障类型识别结果Fig.7 Recognition result of fault type inside and outside

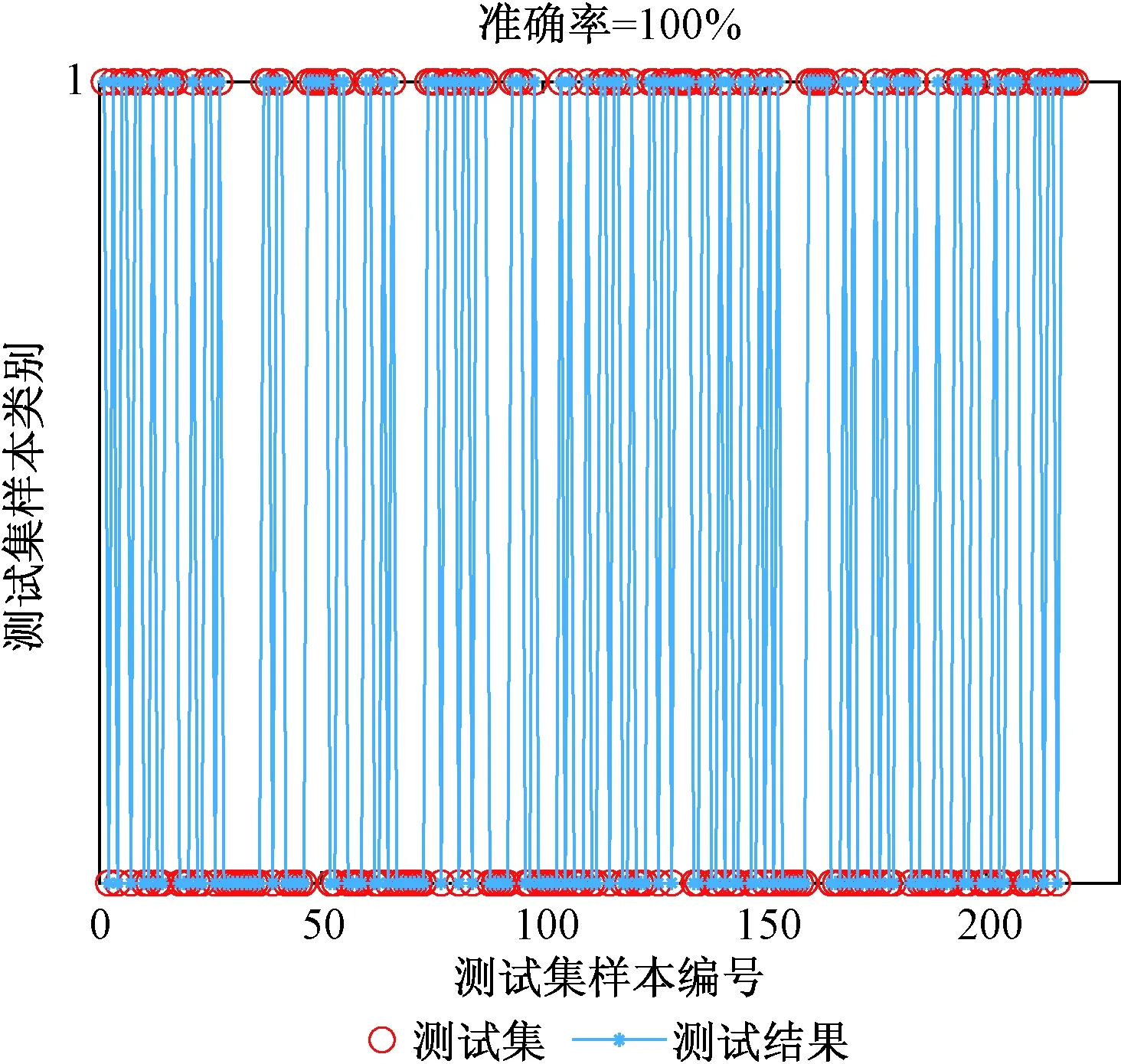
图8 故障极识别结果Fig.8 Fault pole identification result

4.3.1 不同过渡电阻故障辨识分析

分别对发生不同过渡电阻故障进行识别，以此验证辨识方法的耐受过渡电阻能力。分别以发生过渡电阻为1、300和650 Ω的故障为例，故障距离设为600 km。辨识结果如表3所示。

表3的结果表明，所提出的改进VMD-MPE-GRNN故障辨识方法能够准确地识别出不同过渡电阻故障类型，且无论是发生低阻还是高阻故障，该方法都能够准确地识别出故障类型，这表明该方法具有一定的耐受过渡电阻能力。

4.3.2 不同故障距离故障辨识分析

分别对发生不同故障距离故障进行识别，以此验证文中所提出的方法识别不同故障距离故障的能力。故障距离分别以1、320和799 km为例，过渡电阻设为600 Ω。对不同故障距离辨识的结果如表4所示。

表4的结果表明，所提出的改进VMD-MPE-GRNN故障辨识方法能够准确地识别出不同故障距离故障类型，且无论是近距离还是远距离故障都能够准确地识别出故障类型，这表明该方法不受故障距离的影响，在不同故障距离故障识别方面可靠性高。

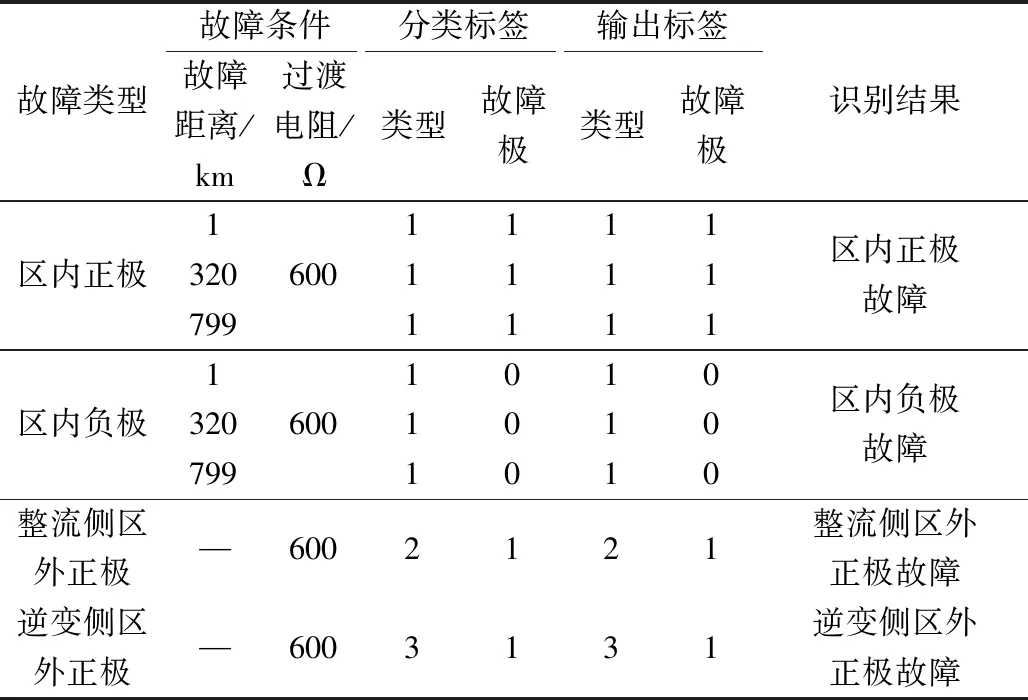
表4 不同故障距离故障辨识结果Table 4 Different fault distance fault identification results

4.4 与其他方法对比分析

为了有效地对比验证提出的改进VMD-MPE-GRNN故障辨识方法的效果，分别采用VMD-RBF、VMD-PNN和GRNN网络对设置的6种故障进行识别，并将识别结果与文中所提方法的识别结果进行对比，结果对比如图9所示。

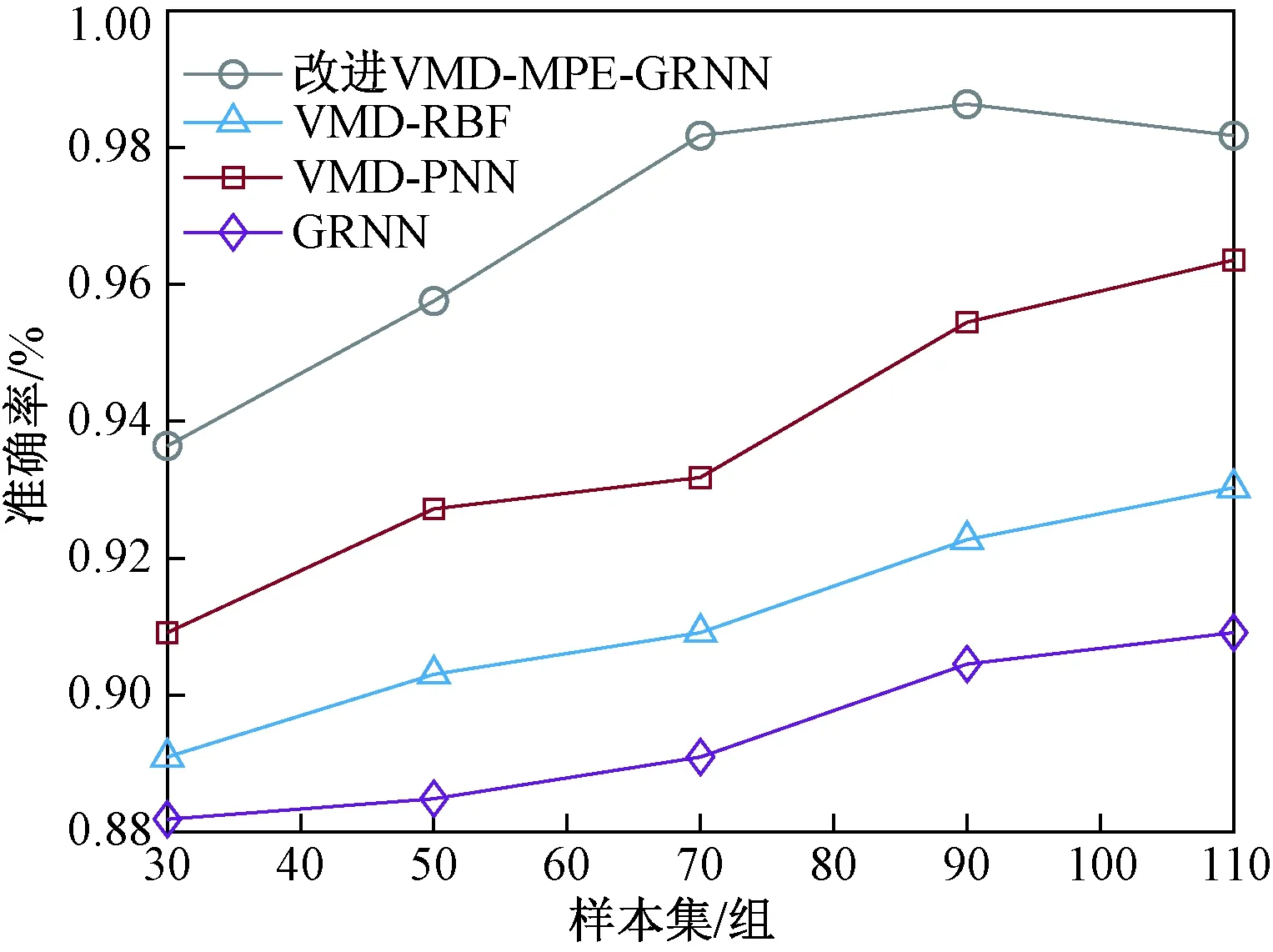
图9 不同网络辨识结果对比Fig.9 Comparison of identification results of different networks

从图9的结果对比可以看出，提出的改进VMD-MPE-GRNN故障辨识方法相对于其他几种网络的辨识准确率更高，这表明所提方法在小样本故障辨识方面的有效性和可靠性更高，相对来说效果优异，具有更好的泛化能力。同时也能看出，利用改进VMD-MPE方法提取故障特征后再利用GRNN网络辨识故障的准确率比直接使用GRNN网络辨识故障的准确率高，说明提取故障特征方法有效，能够提高故障辨识准确率。

5 结论

根据双极HVDC输电系统故障物理边界的特点，利用改进VMD-MPE-GRNN故障辨识方法实现对区内正极故障、区内负极故障、整流侧区外正极故障、整流侧区外负极故障、逆变侧区外正极故障、逆变侧区外负极故障等6种类型故障的准确辨识。首先采用鲸鱼算法改进VMD，解决了传统VMD需要预设K值再用其他方法确定K值以及依据经验设置二次惩罚因子α的问题，通过寻优确定最佳(K,α)参数组合，然后计算IMF分量的2尺度排列熵提取故障特征组成故障特征向量，最后利用故障特征向量输入GRNN故障辨识模型中进行故障类型的辨识，并将所提出的方法与其他方法进行比较分析。实验结果表明，改进VMD-MPE-GRNN故障辨识方法能够准确地辨识出不同类型的故障，且具有一定的耐受过渡电阻能力，在小样本故障辨识方面具有一定的优越性，无需大量的数据进行训练即可准确识别故障，故障辨识的有效性和可靠性高，但所提故障辨识未考虑对双极短路故障的识别，且当故障数据增多时其辨识效果未知，该方法具有一定的局限性，有待考虑更多因素做进一步的提升。