基于自适应调节过零点系数的远聚焦超声成像算法
2022-01-26张亚东郑驰超彭虎
张亚东,郑驰超,彭虎
(1.合肥工业大学生物医学工程系,合肥 230009;2.安徽医科大学第一附属医院医学工程部,合肥 230022)
1 引 言
超声成像作为一种安全性高,成本低,快速便捷的医学诊断方法,在临床上得到广泛的应用[1-2]。传统的超声成像系统根据发射方式的不同,有聚焦线扫描、合成孔径和平面波符合等方式[2-4]。远聚焦像素(FPB)成像是通过阵元阵列延时发射的控制在成像区域外形成的虚拟聚焦点,然后根据焦点位置对被测区域进行成像[5-6]。FrFPB成像相比于传统的成像可以在整个成像深度内提高成像对比度和分辨率等。这些成像方式在接收端均采用延时叠加(delay and sum, DAS)波束形成算法进行成像。DAS是根据阵元通道几何位置关系对所接收的回波信号进行延时量的计算,然后对延时后的数据对齐叠加[3]。它计算简单,成像速度快,但由于其采用固定窗函数加权导致主瓣宽度增加,成像空间分辨率低,成像对比度较差[7-10]。
为了提高成像质量,自适应加权算法的研究越来越多。研究较多的是CF的加权算法。CF最早是一种图像质量的评价指标[11],由于该系数具备较高的噪声抑制能力,后来作为加权系数用于提升成像质量[12-13]。CF类的系数因算法简单,分辨率高,引起了广泛的关注。Li等[14]和吴文焘等[15]研究了广义相干系数(generalized coherence factor, GCF),该算法克服了CF算法的鲁棒性较差的问题,能够有效地减少由于声速不均匀带来的聚焦误差。为了进一步改善超声成像的质量,研究人员相继提出短阶空间相干系数(the short-lag spatial coherence, SLSC)[16-19]、信号特征值系数(signal eigenvalue factor, SEF)[20]、SNR系数[21]。此外,Camacho等[22]提出了相位相干系数(phase coherence factor, PCF),抑制了超声图像中光栅和旁瓣。郑驰超等[4]提出了短阶相干系数(short-lag coherence factor, SLCF),从而可以改善背景组织的成像质量,有效地提高对比度。过零点是一种反应信号稳定性的指标,一般用于信号的模式识别。过零点系数(zeros-crossing factor,ZF) 是根据信号的过零点数设计的加权系数,被用于提升超声成像质量。ZF通过回波信号过零点数来反映信号的相干性,计算简单,背景信噪比高,但是对比度的改善较少[23]。文献[24]提出子阵列过零点系数,将子阵列平滑与过零点系数结合的方式提高成像对比度,但是该方法复杂度较高。
本研究根据CF系数可以准确反应信号相干性这一特点,将其作为调节系数,对ZF系数进行自适应调节,提出一种自适应的过零点系数(aZF)。 相对于传统的加权系数,aZF系数对背景散斑特征的影响较小,并进一步提高了去除噪声和杂波的能力。
2 原理
2.1 FPB成像
FPB的成像方式见图1。
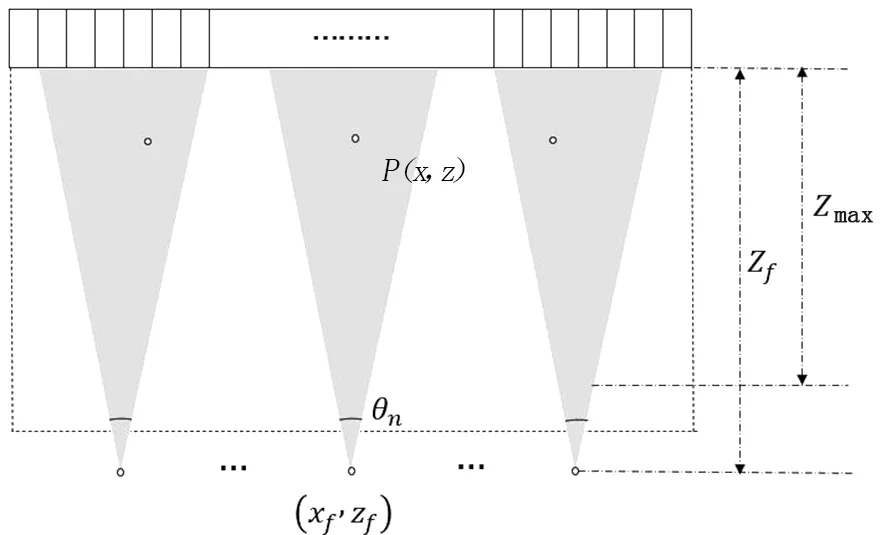
图1 Dtagram of FPB成像方式示意图
设第n次发射时对应的焦点坐标设为(xf,n,zf,n) 。则对于区域内的成像点P(x,z) ,第n次成像过程中,阵列阵元中第m个阵元所接收到回波信号设为sm,n(t),成像延时tp,n计算如下:
(1)
式中,c表示声速,xm为第m个接收阵元的横向坐标。第n次发射时,设P点经过延时后的信号为sm,n(p),则sm,n(p)=sm,n(t-tp,n)。对于第n个焦点,点P(x,z) 的成像输出Sn(p)为:
(2)
式中M为接收阵元的数量。向量S(p)表示成像点p的N次发射成像结果,S(p)=[S1(p),S2(p),......,SN(p)] ,因此,FPB的成像结果由下式可得:
(3)
2.2 CF和ZF加权算法
CF定义为成像系统的回波相干信号强度与总的信号强度的比值。在FPB成像中,根据向量Sn(p) ,给出适用于FPB的CF计算公式如下:
(4)
从式(4)中可以得到相干系数的取值范围为0~1,当所有通道回波信号相同时,CF值为1,当所有通道回波信号为0时,CF值为0。由文献[4]可知,CF加权算法对于点目标能够得到较高的分辨率,但对散斑目标,由于低频区域中含有主瓣信号,将导致CF加权算法中相干信号能量降低。
设ZP为向量S(p)的过零点数,向量S(p)的元素数最大为N,则可知向量S(p)的最大过零点数ZPmax为N-1,则可知ZP≤N-1。过零点数ZP可以反应噪声的强度,ZP值越大,则表示超声回波信号中噪声越大。据此ZF系数由下式可得:
(5)
由上式可知,ZF值在0到1之间。对于噪声,ZP值较大,ZF值较小,而对相干性较好的有效信号,ZP一般接近0,因此ZF值接近1。
由式(3)、式(4)、式(5)可得,CF和ZF对FPB算法的加权输出结果分别如下:
YCF(p)=CF(p)YFPB(p)
(6)
YZF(p)=ZF(p)YFPB(p)
(7)
2.3 aZF加权算法
为了抑制噪声,提高有效信号的作用,本研究提出了aZF加权算法,设置调节系数δ,δ的公式如下:
(8)
δ根据信号的CF系数进行变化,由式(4)可知,δ的值范围在0~1之间。考虑到CF系数对背景组织的信号相干性估计偏低,因此,我们对CF系数进行取平方根处理后作为调节系数,提高适应性。
采用δ进行成像点的最大过零点数ZPmax进行调节。由式(4)和式(5)可知,可由下式得到aZF:
(9)
其中,为了保证aZF值在0~1之间,当ZP≥(N-1)·δ时,aZF设为0。
对于相干性较高的有效信号,CF值较大,即δ较大,ZP较小,因此aZF为较大值,接近于1。对于噪声信号和杂波,ZP值大,δ值小,根据式(9)可知,aZF的值接近于0或等于0。因此,将aZF做为加权系数能较好的抑制噪声和去除杂波。由式(3)、式(9)可得到aZF对FPB算法的加权输出结果如下:
YaZF(p)=aZF(p)YFPB(p)
(10)
3 实验结果
3.1 实验设置
本研究点和斑的仿真数据是通过FieldⅡ软件产生[25-26]。利用数据采集系统(Sonix-Touch)采集所需要的实验数据,实验数据是通过阵列传感器模型(L14-5/38)在体膜(KS107BG)和人体组织中获得。在设置仿真系统的参数时,为确保数据的一致性,其参数的设置与实验系统参数设置基本相同。成像系统参数设置见表1。本研究通过对DAS、CF、ZF和aZF加权算法之间的4个不同的成像质量作比较。同时在成像过程中将10 dB信噪比的高斯白噪声加到回波信号中,且将全部成像算法的动态范围设置为60 dB。

表1 超声成像系统参数
本研究为了评估成像性能,采用能够反映分辨率的半峰值宽度(full-width at half-maximum, FWHM, 即-6 dB波束宽度)[4,27]、主要表现暗斑内部平均强度与外部背景的平均强度之差的对比度(contrast ratio, CR)[28]、主要反映成像信噪比与对比度的综合指标的噪声对比度(contrast-to-noise ratio, CNR)[24,27]和反映背景组织信噪比成像质量的散斑信噪比(speckle signal noise ratio, SSNR)等指标进行评估。CR、CNR和SSNR的公式如下[24,27]:
CR=|μb-μc|
(11)
(12)
(13)
其中,μb为背景区域的平均强度,μc为吸声暗斑内部的强度,δb为背景区域强度的标准差,δc为暗斑内部成像强度的标准差。
3.2 仿真结果
3.2.1仿真点成像 设置仿真点的成像区域横向距离为-4~4 mm,深度为10~35 mm,且成像区域内有5个散射点,见图2。从成像结果可知,CF、ZF和aZF加权算法对散射点的成像效果均比DAS算法好。

图2 散射点的仿真成像结果
为了更直观地表现出4种算法的成像性能的差异,对设定两个散射点坐标(0 mm,15 mm)、(0 mm,30 mm)的横向强度变化进行比较分析,见图3。DAS算法的横向宽度略大于其他3种算法,其中aZF和ZF加权算法的横向宽度次之。三种加权算法中最小的横向宽度为CF加权算法。本研究表示出设定的两处散射点的横向FWHM值,见表2。CF加权算法对不同深度成像点的横向分辨率均优于其他各算法,在近场ZF加权算法的分辨率与aZF加权算法一致,而在远场中aZF加权算法的分辨率略优于ZF加权算法,但差异很小。DAS算法分辨率最差。
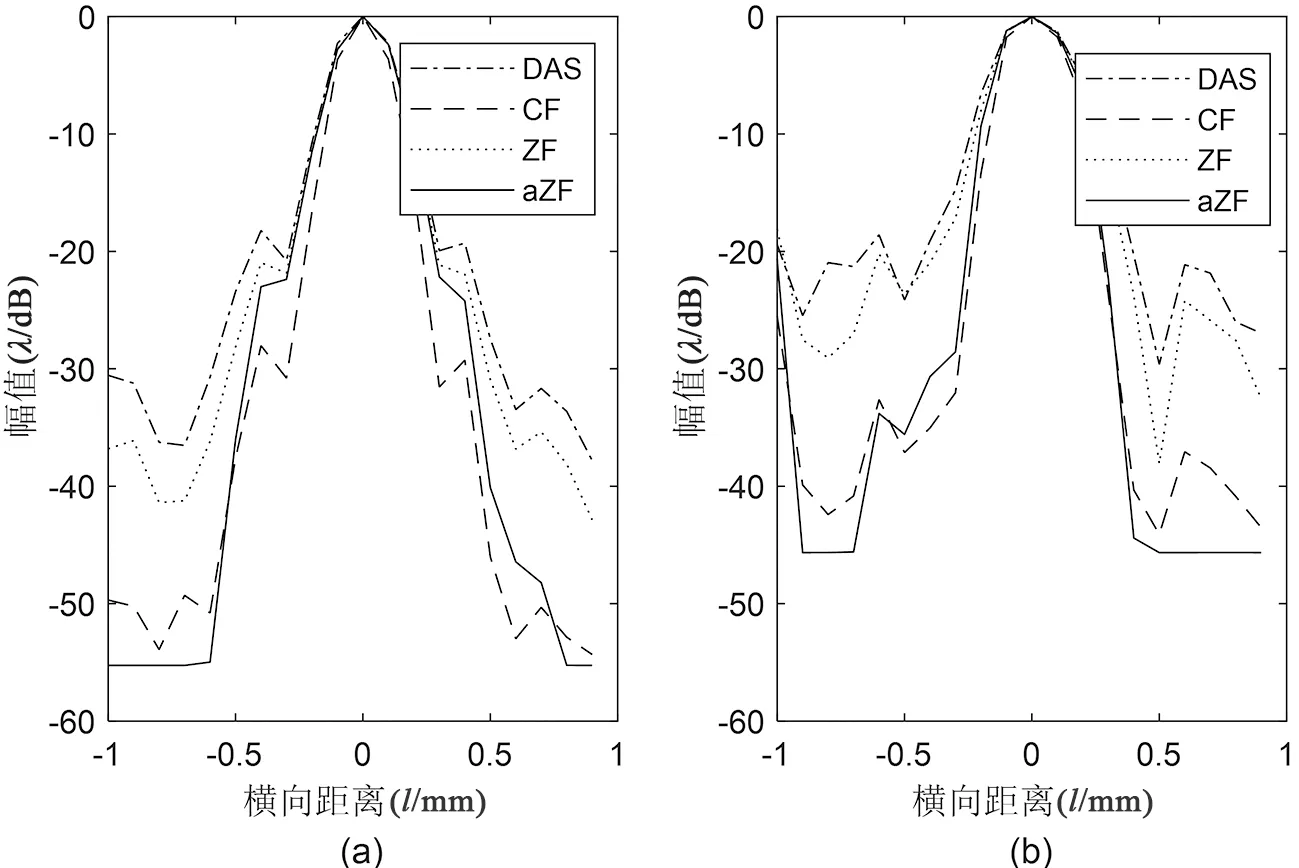
图3 仿真点横向强度变化
3.2.2仿真斑成像 本研究设置斑仿真的成像区域横向距离为-4~4 mm,深度为15~35 mm,且成像区域内有3个圆形暗斑,见图4。相对于DAS算法,CF、ZF、和aZF加权算法成像暗斑边界较清晰,内部噪声较小,对比度较好。同时,随着成像区域深度的增加,CF加权算法的背景组织成像效果有所下降,而ZF、aZF加权算法背景组织成像质量相对较好。
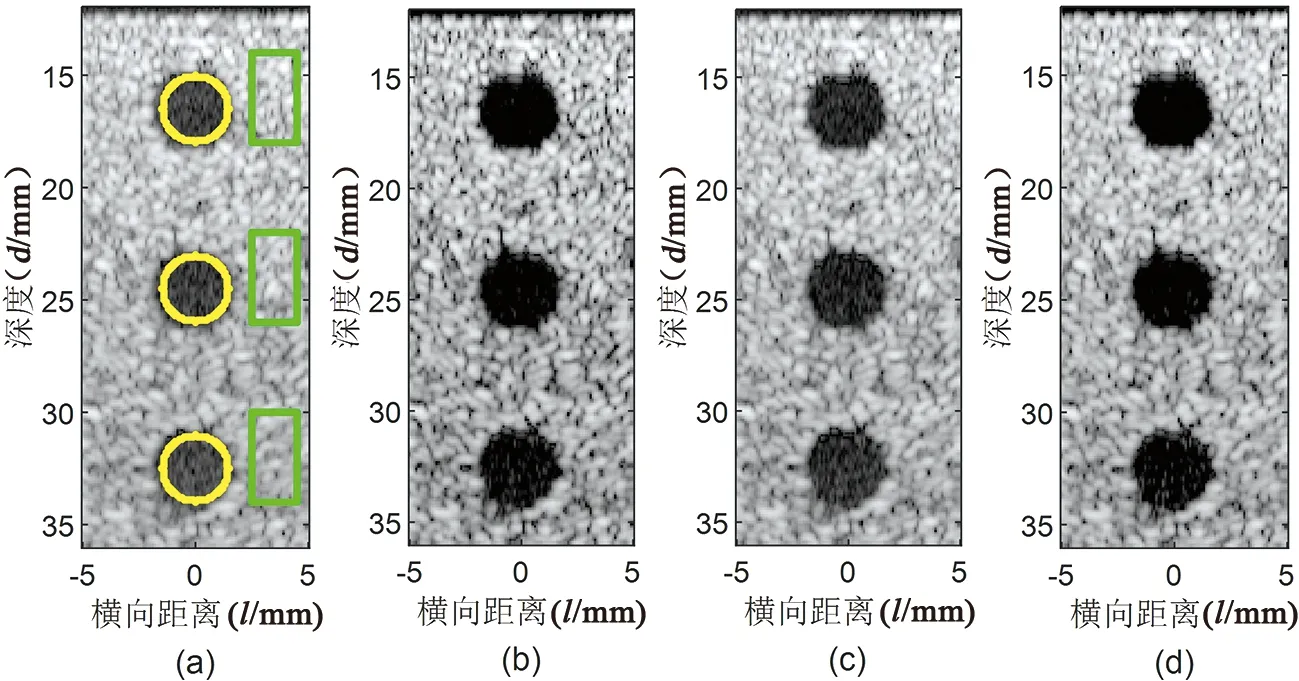
图4 暗斑的仿真成像结果

表2 仿真散射点的横向FWHM值
随着成像深度的增加,仿真斑的CR、CNR和SSNR系数的结果见表3 。相比于DAS算法,CF、ZF、aZF加权算法在CR上均有明显的地提高,而CNR、SSNR均有所下降。对于近场的暗斑来说,CR分别提高了15.56、5.14、18.48 dB,上升了约50.0%、16.5%、59.3%,而CNR分别下降了0.34、0.06、0.11 dB,降低了约20.2%、3.6%、6.5%,SSNR分别下降了0.39、0.08、0.15 dB,降低了约22.5%、4.6%、8.7%。对于远场的暗斑来说,CR分别提高了13.08、5.01、16.09 dB,上升了约55.0%、21.1%、67.6%,而CNR分别下降了0.32、0.09、0.14 dB,降低了约17.9%、5.0%、7.8%,SSNR分别下降了0.43、0.25、0.25 dB,降低了约22.4%、13.0%、13.0%。由此可见CF、ZF、aZF加权算法相比于DAS算法,对远场背景组织对比度提升的效果比近场明显,而近场背景组织均匀性下降的较为缓慢。对比CR、CNR和SSNR系数,除ZF加权算法中CR值下降外,ZF和aZF加权算法基本上都要高于CF算法,对于ZF加权算法,在近场中CR下降了10.42 dB,降低了约22.3%,CNR和SSNR分别提高了0.28、0.31 dB,上升了约20.9%、23.1%,在远场中,CR下降了8.07 dB,降低了约21.9%,CNR和SSNR均提高了0.23、0.18 dB,上升了约15.6%、12.1%。对于aZF加权算法,在近场中分别提高了2.92、0.23、0.24 dB,上升了约6.3%、17.2%、17.9%,在远场中分别提高了3.01、0.18、0.18 dB,上升了约8.2%、12.2%、12.1%。综上可见,ZF、aZF加权算法的背景组织成像质量优于CF,ZF的背景组织质量略优于aZF,但差异较小。ZF对比度则明显低于aZF算法。
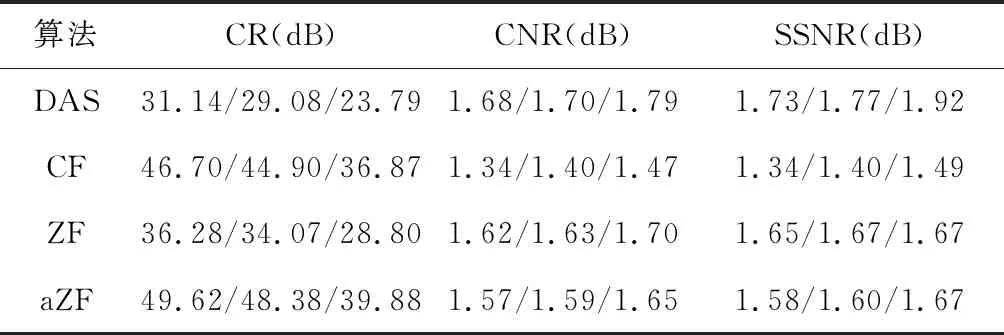
表3 仿真斑的CR,CNR和SSNR
3.3 实验成像
3.3.1实验点成像 设置实验点的成像区域横向距离为-5~5 mm,深度为0~40 mm,且成像区域内有3个散射点,见图5。相比于DAS成像算法,其他加权算法对实验散射点的成像效果较好。在远场区域,CF加权算法背景组织成像的质量有所下降,而ZF、aZF加权算法对不同深度的背景组织成像效果较为均匀。
为了将4种算法的成像性能的差异更直观的表现出来,对设定两个散射点坐标(1 mm,10 mm)、(1 mm,30 mm)的横向强度变化进行比较分析,见图6。DAS算法的横向宽度最大,CF算法的横向宽度最小,ZF和aZF加权算法的宽度相对略小一些。本研究表示出设定的两处散射点的横向FWHM值,见表4。从横向FWHM值中可以得出,CF加权算法的横向分辨率略优于DAS、ZF与aZF加权算法,ZF加权算法的横向分辨率和aZF加权算法的横向分辨率相似,DAS算法分辨率相对较差。

图5 散射点实验成像结果

图6 仿真点横向强度变化

表4 实验点的横向FWHM值
结合以上仿真点与实验点的成像结果、横向强度变化可知,仿真与实验的结果基本一致。其中CF、ZF与aZF加权算法对点成像的效果相比于DAS算法略有提升,CF加权算法的横向分辨率相比于DAS算法较好,且略优于ZF与aZF加权算法。DAS算法和ZF、aZF加权算法的横向分辨率差异较小,这是因为成像系统在轴的信号的过零点数差异较小,因此,ZF加权算法对横向分辨率的改善较弱,aZF加权算法用CF调节ZF,其算法本质上也是基于过零点数设计,因此,分辨率与ZF加权算法差异较小。
3.3.2实验斑成像 在设定的成像区域内实验斑的成像效果,见图7。CF、ZF和aZF加权算法的成像的结果相对于DAS算法边界较清晰,内部噪声不明显。ZF和aZF加权算法相比于CF加权算法,背景组织的成像质量较好,斑轮廓相对清晰。
实验斑成像的CNR、CR和SSNR结果,见表7。相比于DAS算法,CF、ZF和aZF加权算法在CR结果上提高了11.07、3.96、15.10 dB,上升了约65.0%、23.3%和88.7%。CF加权算法相比于DAS算法在CNR和SSNR下降了0.25、0.40 dB,降低了约23.1%、31.5%。因此,CF算法背景组织成像质量较差。相比于CF算法,ZF和aZF加权算法在CNR上提高了0.19、0.12 dB,提升了约22.9%、14.5%,在SSNR上提高了0.25、0.11 dB,提升了约28.7%、12.6%,在CR上,ZF加权算法下降了7.11 dB,降低了约25.3%,aZF加权算法提高了4.03 dB,提升了约14.3%。而DAS算法的CNR、SSNR最高,ZF和aZF加权算法其次。相对于ZF算法,aZF算法在CNR和SSNR降低了约6.9%、12.5%,而CR提高了53.1%。由此可见,aZF加权算法提高了成像的对比度,而背景组织成像的均匀性基本保持不变。

图7 实验斑成像结果

表5 实验斑的CR、CNR和SSNR
综合仿真斑和实验斑的成像效果及CR、CNR、SSNR的数据可知,仿真与实验斑的成像均表现为,CF、ZF与aZF加权算法的成像质量优于DAS算法。相比于DAS算法,CF、ZF、aZF加权算法均改善了暗斑的对比度,其中CF和aZF加权算法对暗斑对比度的提升程度明显大于ZF加权算法,aZF加权算法大幅提升了图像的CR,对暗斑的对比度改善最大。相比于CF加权算法,aZF加权算法在CR、CNR和SSNR上都有所提高,暗斑的对比度、均匀性及抑制噪声的能力均有所提升,且暗斑对比度增强的幅度大于抑制噪声能力提升的程度。相比于ZF加权算法,aZF加权算法斑内噪声抑制能力明显提升,暗斑的对比度明显增强,而背景成像质量略有下降。
3.3.3人体组织成像 本研究选用人体颈动脉作为人体组织成像,其成像结果见图8。相对于DAS算法,CF、ZF和aZF加权算法成像的人体颈动脉轮廓相对较为清晰,与周围其他组织分界较为明显。CF加权算法的背景组织成像中存在黑色斑点噪声,ZF和aZF加权算法背景组织成像中的黑色斑点噪声相对不明显。

图8 人体颈动脉实验成像结果
人体颈动脉成像的CNR、CR和SSNR的结果见表6,可以看出CF、ZF和aZF加权算法CR值均高于DAS算法,分别提高了23.65、3.70、36.35 dB,提升了约117.3%、18.3%、180.2%。CF加权算法在CNR和SSNR上均略低于其他算法,相比于DAS算法,CNR和SSNR下降了0.21、0.34 dB,降低了约19.4%和28.1%。相比于CF算法,ZF和aZF加权算法在CNR分别提高了0.17、0.16 dB,上升了约19.5%和18.4%,在SSNR上分别提高了0.25、0.16 dB,上升了约28.7%和18.4%。同时,DAS算法在CNR、SSNR上依然均高于其他算法。
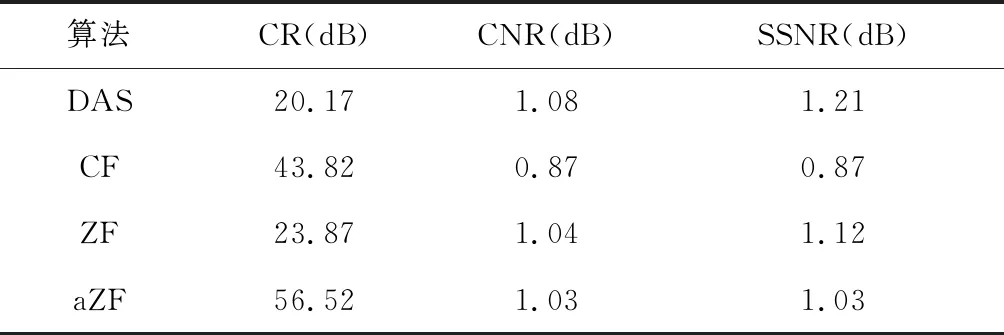
表6 人体颈动脉实验CR、CNR和SSNR
综上所述,结合人体颈动脉实验、实验斑和仿真斑结果可知,人体颈动脉成像结果与仿真和实验斑成像结果基本一致。aZF加权算法在背景组织成像质量上表现较好,并且具有很好的抑制噪声能力,在三种加权算法中暗斑的对比度的提升幅度最大。背景组织均匀性明显高于CF加权算法,略低于ZF算法。
4 结束语
本研究提出了一种aZF加权的远聚焦像素成像算法,该算法是根据相干系数可以有效反应信号相干性的特点,将其作为调节系数,对结合信号过零点数所生成ZF进行调节的加权算法。该算法相比于DAS算法有着较好的对比度,相比于CF加权算法有着较好的CR、CNR和SSNR,有效地提升了背景组织的对比度及抑制噪声。相比于ZF加权算法有着较好的CR,同时能够保持CNR和SSNR基本不变。后续我们将继续研究能够和ZF、CF相结合的新的加权算法,进一步提高成像的质量。
