三种典型悬挑脚手架支撑体系的对比分析

耿大将， 龙敏健， 金学胜， 刘 融， 杨 兵

（1.中建四局第六建设有限公司，上海 201100； 2.中国建筑第四工程局有限公司，上海 201100）

脚手架在建筑结构施工尤其是住宅建筑施工中具有十分重要的作用. 按照作用原理的不同，建筑脚手架目前主要包括附着式升降架、爬架和悬挑架等形式［1-3］. 而悬挑架根据其受力体系的不同可以分为完全悬挑式、下撑悬挑式、上拉悬挑式及下撑上拉悬挑式［4-6］. 完全悬挑式脚手架在实际工程中应用最为广泛［7］，但是该类脚手架需要在墙体和楼板开洞，对建筑结构有损害并且存在后期渗漏风险. 为了解决完全悬挑式脚手架的这些问题，国内外学者提出了下撑悬挑式脚手架［4-5，8］和上拉悬挑式脚手架［9-12］. 目前对完全悬挑式脚手架的设计、安装、使用、监测工作的研究［13-22］较为充分，工程实际应用经验也较为丰富. 然而对下撑悬挑式脚手架和上拉悬挑式脚手架虽然在工程实践中也有所应用，但目前的研究主要集中在工程施工方面，这两类脚手架的设计方法仍然参照完全悬挑式脚手架的设计方法. 考虑到完全悬挑式脚手架、下撑悬挑式脚手架和上拉悬挑式脚手架的支撑体系是不同的，直接应用完全悬挑式脚手架的设计计算方法对下撑悬挑式脚手架和上拉悬挑式脚手架进行设计显然是不合理的.

此外，在实际工程实践中都希望能低成本快速完成脚手架的搭拆工作，对三种典型悬挑脚手架支撑体系进行构造对比、受力对比、效益对比，不仅可以给相关设计工作参考，而且可以给工程界对脚手架支撑体系的选择提供借鉴作用.

1 三种支撑体系的构造对比分析

悬挑式脚手架、下撑悬挑式脚手架和上拉悬挑式脚手架的构造分别如图1（a）、图1（b）和图1（c）所示.从图中可以明显看出，三类脚手架的传力体系是较为类似的，均为脚手板→横向水平杆→纵向水平杆→立杆→承载梁，所不同的是承载梁将力传递给建筑结构的方式.

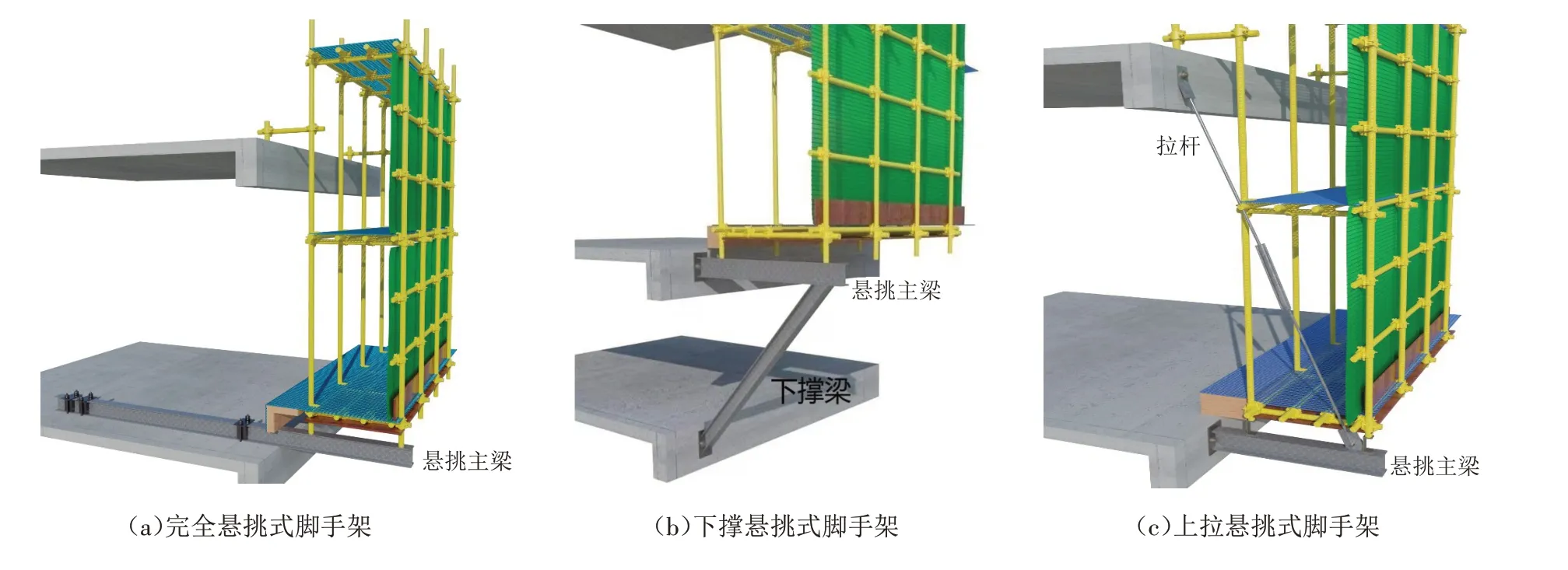
图1 三种脚手架支撑体系对比Fig.1 Comparison of three kinds of scaffolds

对如图1（a）所示的完全悬挑式脚手架，承载梁承受的荷载会直接传递给建筑结构楼板和墙体. 承载梁与建筑结构楼板之间一般通过3个U型螺栓加以固定. 对如图1（b）所示的下撑悬挑式脚手架，悬挑承载梁承受的荷载会部分传递给下撑梁，然后将荷载通过下撑梁和悬挑梁共同传递给建筑结构. 下撑梁与建筑结构墙体间、悬挑梁与建筑结构墙体间、下撑梁与悬挑梁之间均通过螺栓实现固定连接. 对如图1（c）所示的上拉悬挑式脚手架，悬挑承载梁承受的荷载会部分传递给上拉杆，然后荷载会通过上拉杆和悬挑梁传递给建筑结构. 悬挑梁与建筑结构墙体间通过螺栓实现固定连接，上拉杆与建筑结构墙体（或梁）间通过螺栓实现铰接连接，上拉杆与悬挑梁通过螺栓铰接连接.

综上分析可以看出，三种脚手架体系最大的不同在于支撑体系的不同，而支撑体系的不同会导致力传递路径、脚手架受力、安拆施工工序、施工周期、经济效益及社会效益等的不同.

2 三种支撑体系的整体受力分析

2.1 完全悬挑式支撑体系受力分析及验证

2.1.1 受力分析 可以将如图1（a）所示的完全悬挑式脚手架的支撑体系受力图简化为图2 所示［13］. 图中Fn表示立杆传递的集中力，q表示悬挑主梁的自重线荷载，lc和lb分别表示悬挑主梁锚固点中心距离楼板支撑点、梁自由端的距离，lni和lno分别表示内立杆和外立杆距离悬挑主梁锚固点中心的距离.

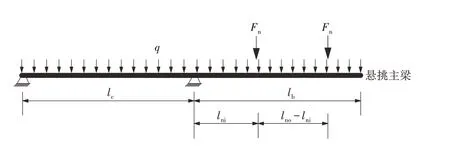
图2 完全悬挑式支撑体系受力简图Fig.2 Force diagram of fully overhanging support system

对图2所示的受力简图进行分析易得悬挑主梁的弯矩为

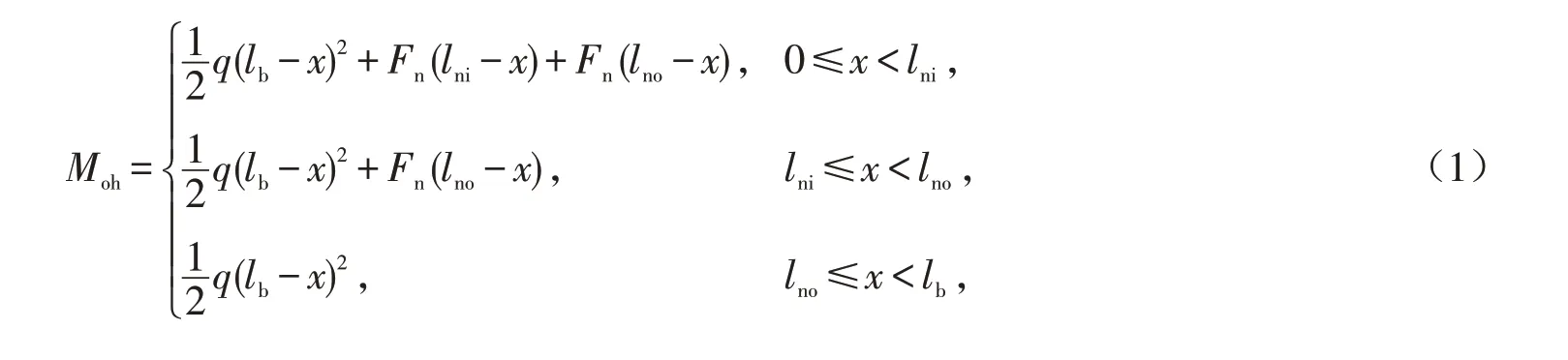
剪力为

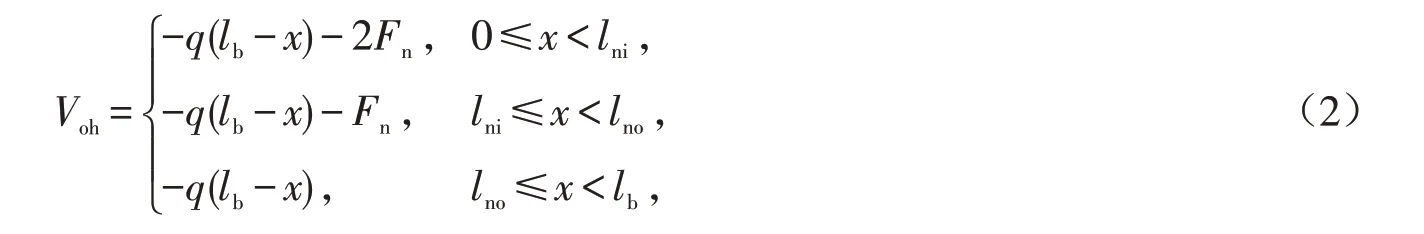
自由端挠度为

式中：x表示悬挑主梁截面距锚固点中心的距离；E表示悬挑主梁的弹性模量；I表示悬挑主梁的截面惯性矩.2.1.2 有限元验证 有限元计算方法是一种十分重要的现代数值计算方法，在工程实际中应用广泛［21-22］. 其具有实施成本低、获得信息全面的优点，在采用式（1）～式（3）完全悬挑式支撑体系进行受力分析之前，有必要采用有限元计算方法对其计算准确性和精度加以验证.

采用有限元分析方法对如图2所示的支撑体系进行受力分析. 所采用的几何参数如表1所示. 具体的在有限元计算中，悬挑主梁为一侧带悬臂的铰接单跨梁，悬挑主梁为I16 工字钢，采用2 节点线性梁单元模拟. 主梁采用理想弹塑性本构模型，弹性模量为206 GPa，泊松比为0.30，屈服应力为235 MPa. 集中荷载设计值为Fn=20.00 kN，自重荷载设计值q=0.246 kN/m .

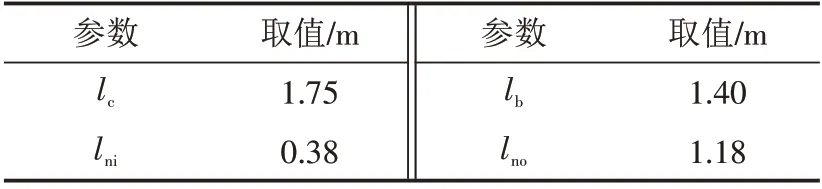
表1 完全悬挑式支撑体系计算参数Tab.1 Calculation parameters for fully overhanging support system

按照式（1）计算得出的弯矩图和有限元计算得出的弯矩图对比如图3 所示. 按照式（3）计算得出的挠度和有限元计算得出的挠度分别为17.86 mm 和18.70 mm.无论从弯矩对比还是从挠度计算结果的对比，可以看出式（1）～式（3）用于计算完全悬挑式支撑体系的内力和变形均具有较高的计算精度.

图3 有限元和理论计算结果对比Fig.3 Comparison of finite element and theoretical calculation results

2.2 下撑悬挑式支撑体系受力分析及验证

2.2.1 受力分析 将如图1（b）所示的下撑悬挑式脚手架的支撑体系简化为图4所示的受力简图. 图中h表示下撑梁与建筑结构固接点到悬挑主梁与建筑结构固接点之间的竖向距离，lbs表示下撑梁与悬挑主梁连接位置到悬挑主梁与建筑结构固接点之间的水平距离.

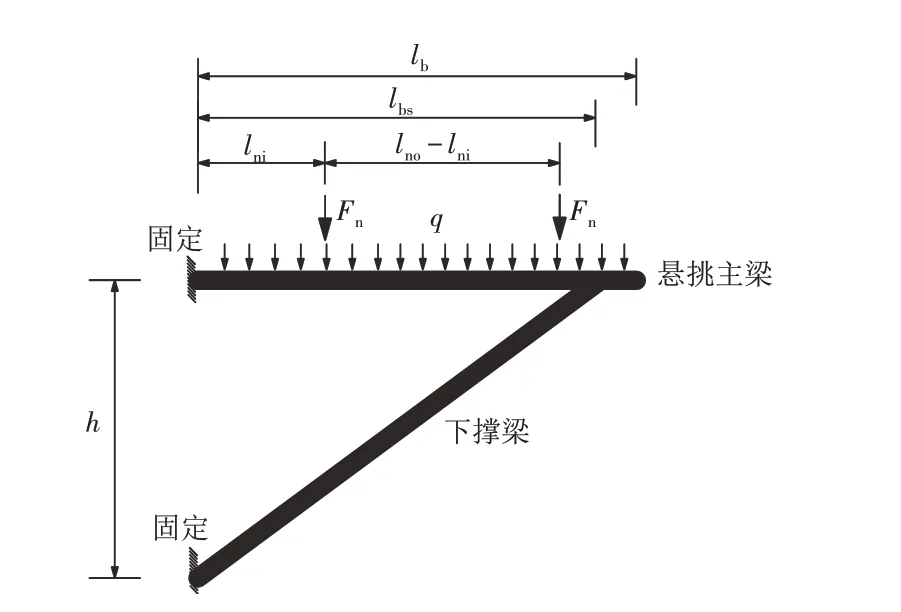
图4 下撑悬挑式支撑体系受力简图Fig.4 Force diagram of bottom support cantilever support system

考虑下撑梁与悬挑主梁连接位置处的转角协调关系、两个方向的位移协调关系、力平衡关系，易得下撑梁与悬挑主梁连接处，下撑梁所受的轴向力为

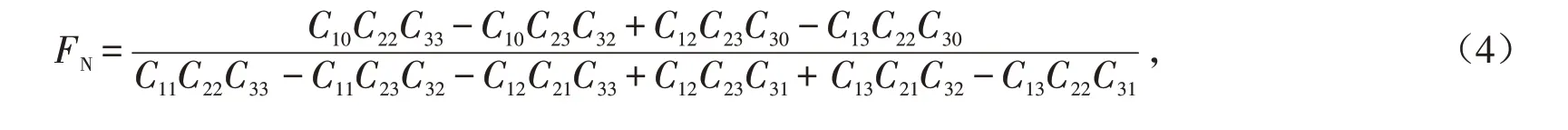
剪力为

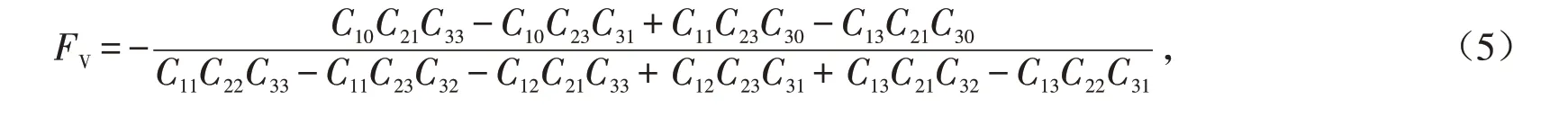
弯矩为

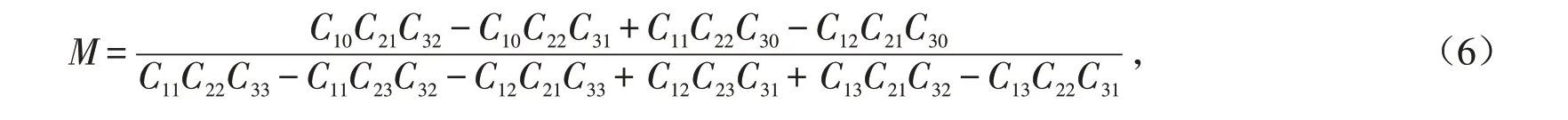
其中：过程变量C11、C12、C13、C10、C21、C22、C23、C31、C32、C33、C30分别为

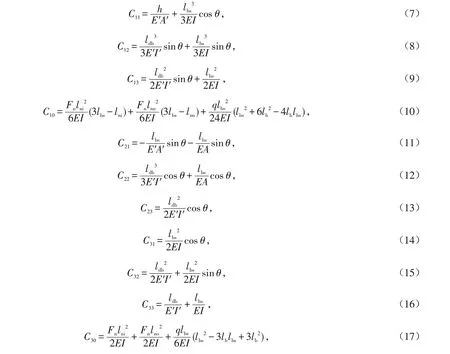
式中：θ表示下撑梁轴向方向与竖直方向的夹角，满足tanθ=lbs/h；ldb表示下撑梁的长度；E′表示下撑梁的弹性模量；I′表示下撑梁的截面惯性矩；A和A′分别表示悬挑主梁和下撑梁的截面面积.

在得出节点处的受力后，易得悬挑主梁的弯矩为

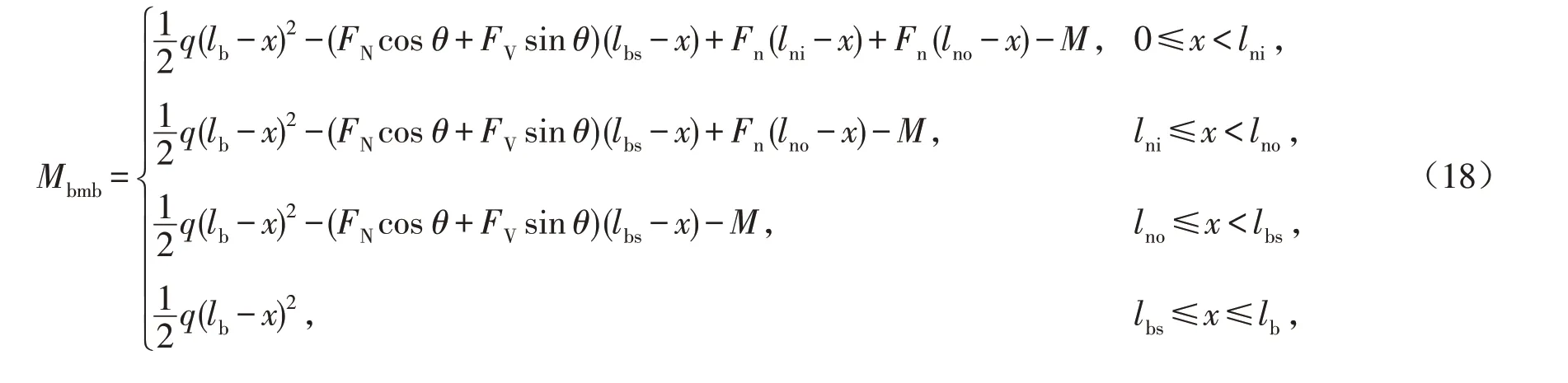
剪力为

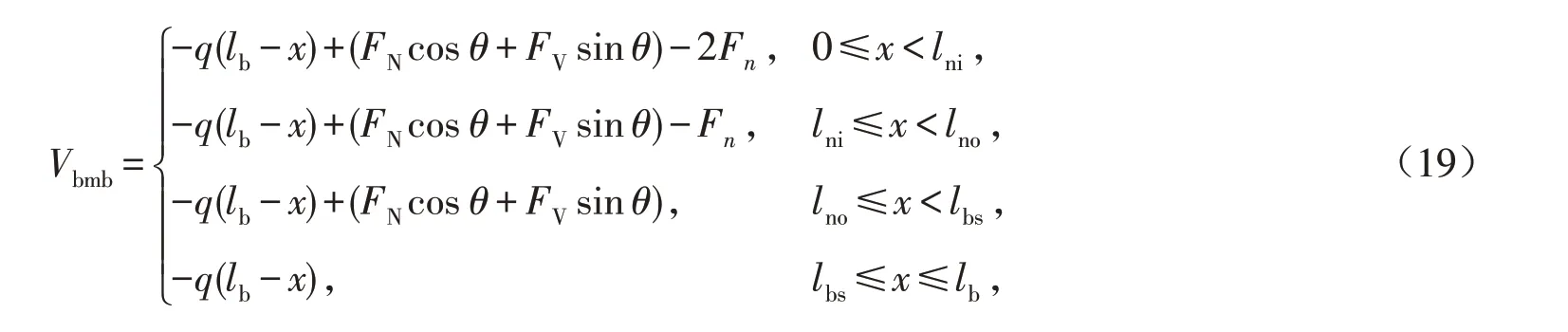
轴力为

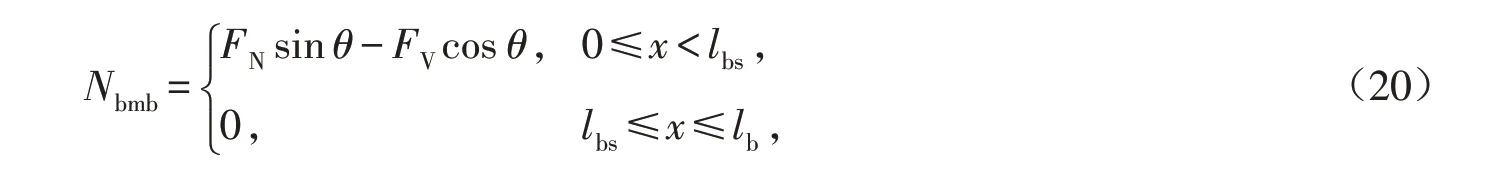
自由端挠度为

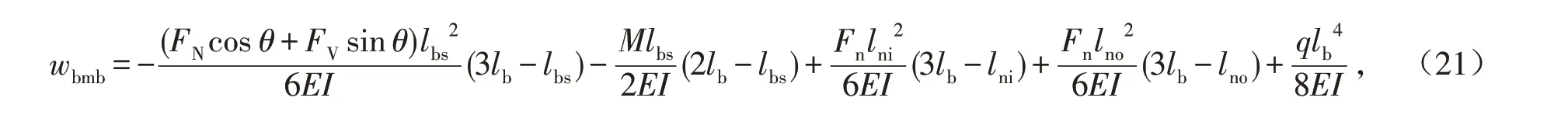
其中：x表示悬挑主梁内力截面点离悬挑主梁固接端的水平距离.下撑梁的弯矩为

剪力为

轴力为

其中：x′表示下撑梁内力截面点离下撑梁固接端的水平距离.

2.2.2 有限元验证 同样采用有限元方法对下撑悬挑式支撑体系的内力计算式（18）～式（20）和挠度计算式（21）加以验证，所采用的计算参数如表2所示. 悬挑主梁和下撑梁均采用工字钢，均采用2节点线性梁单元模拟，悬挑主梁为I16工字钢，下撑梁为I10工字钢. 在有限元计算中边界条件为悬挑主梁和下撑梁与建筑结构连接部位均为固接，悬挑主梁和下撑梁间也为固接连接. 悬挑主梁和下撑梁均采用理想弹塑性本构模型，弹性模量为206 GPa，泊松比为0.30，屈服应力为235 MPa. 集中荷载设计值为Fn=20.00 kN，自重荷载设计值q=0.246 kN/m.

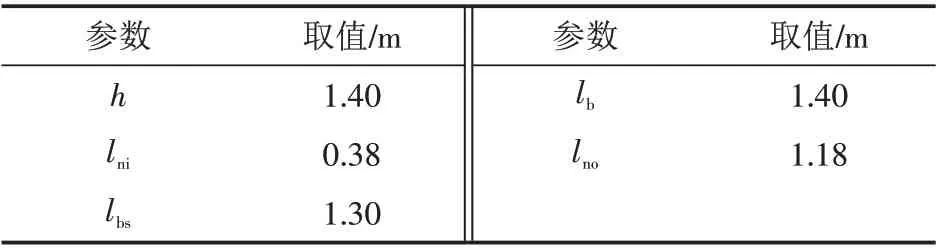
表2 下撑悬挑式支撑体系计算参数Tab.2 Calculation parameters for bottom support cantilever support system

按照式（18）计算得出的悬挑主梁弯矩图和有限元计算得出的弯矩图对比如图5所示. 按照式（21）计算得出的挠度和有限元计算得出的挠度分别为0.36 mm 和0.25 mm. 从图5的弯矩对比可以看出，解析法计算得出的弯矩偏大，但最大误差也在10%以内，完全可以满足工程设计精度要求.

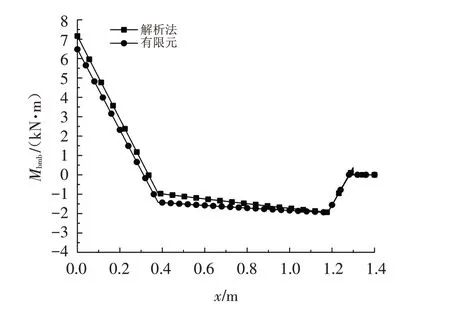
图5 有限元和理论计算结果对比Fig.5 Comparison of finite element and theoretical calculation results

2.3 上拉悬挑式支撑体系受力分析及验证

2.3.1 受力分析 将如图1（c）所示的上拉悬挑式脚手架的支撑体系简化为图6 所示的受力简图. 图中h′表示上拉杆与建筑结构铰接点到悬挑主梁与建筑结构固接点之间的竖向距离，lppo表示上拉杆与悬挑主梁连接位置到悬挑主梁与建筑结构固接点之间的水平距离，lpro表示拉杆长度.

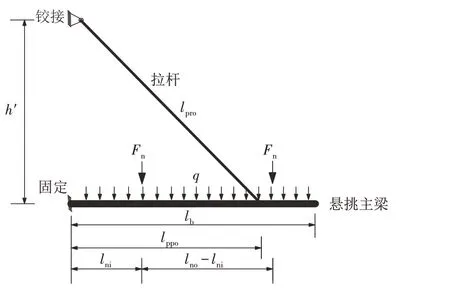
图6 上拉悬挑式支撑体系受力简图Fig.6 Force diagram of pull-up cantilever support system

考虑上拉杆与悬挑主梁连接位置处的竖向位移协调和力平衡条件，易得拉杆的拉力为

θo满足

如图6所示Epro表示拉杆的弹性模量；Apro表示拉杆的横截面面积.

得出拉杆拉力后，将拉杆拉力视为外力，容易得出悬挑主梁的弯矩为

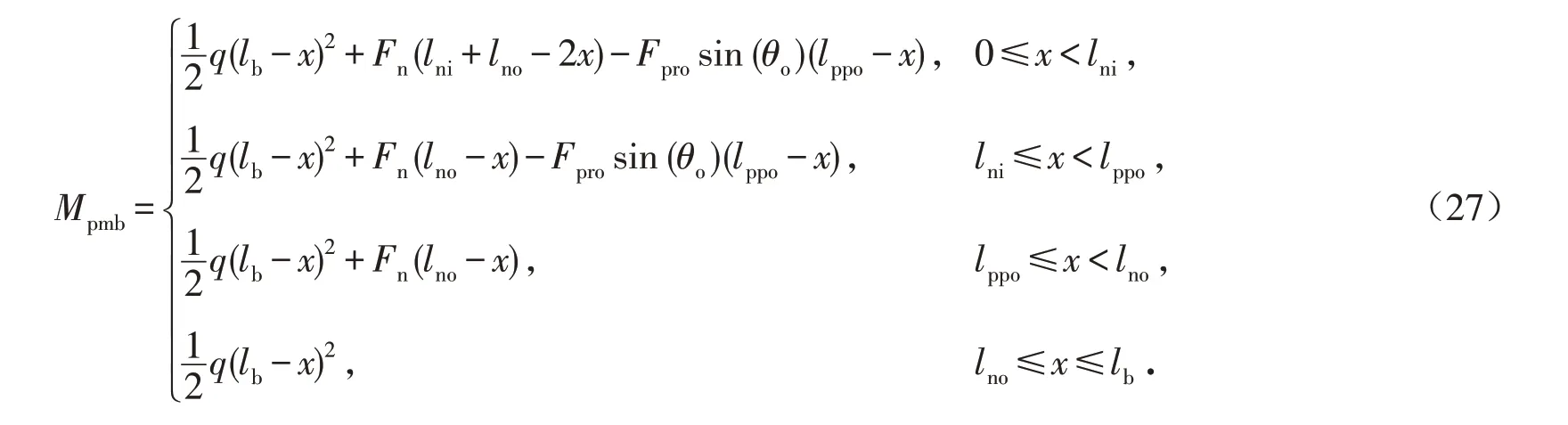
以距离悬挑主梁固接端的水平距离x为变量，对式（27）进行求导，易得悬挑主梁剪力

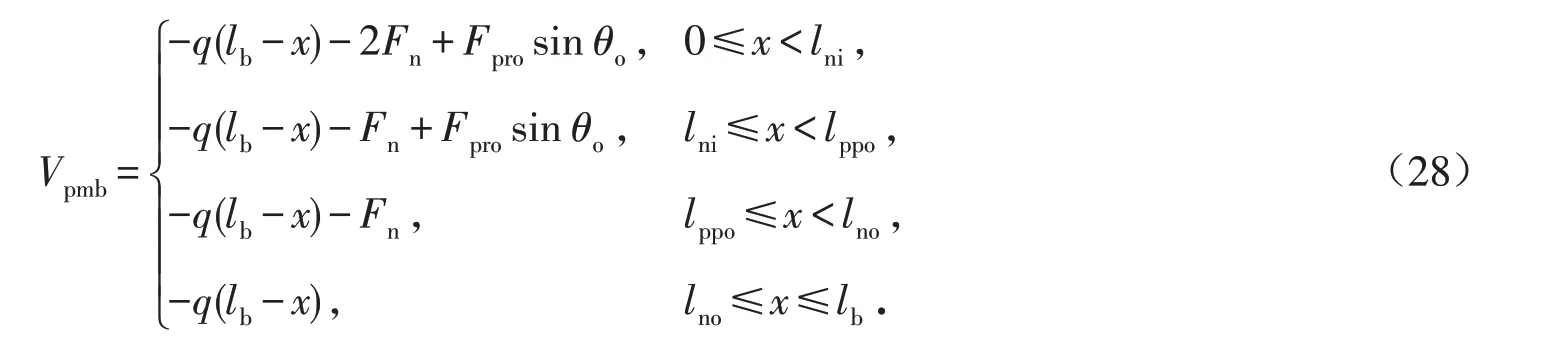
悬挑主梁的轴力为

悬挑主梁的最大挠度在梁自由端，为

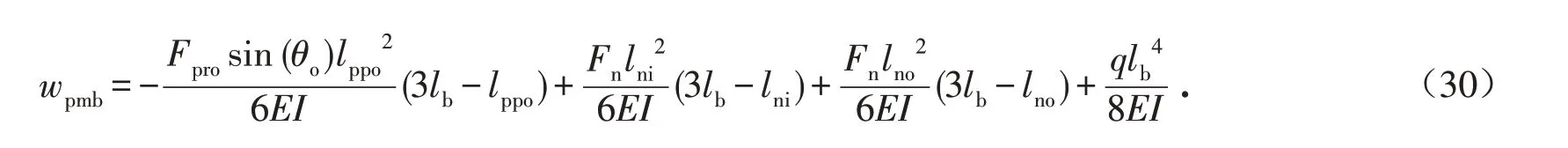
2.3.2 有限元验证 同样采用有限元方法对上拉悬挑式支撑体系的内力计算式（27）～式（29）和挠度计算式（30）加以验证，所采用的计算参数如表3 所示. 悬挑主梁采用I16工字钢，采用2节点线性梁单元模拟，上拉杆直径20 mm的圆钢，采用2节点杆单元模拟. 具体的，在有限元计算中边界条件为悬挑主梁与建筑结构连接部位固接，上拉杆与悬挑主梁、上拉杆与建筑结构之间铰接连接. 悬挑主梁和上拉杆均采用理想弹塑性本构模型，弹性模量为206 GPa，泊松比为0.30，屈服应力为235 MPa. 集中荷载设计值为Fn=20.00 kN，自重荷载设计值q=0.246 kN/m.

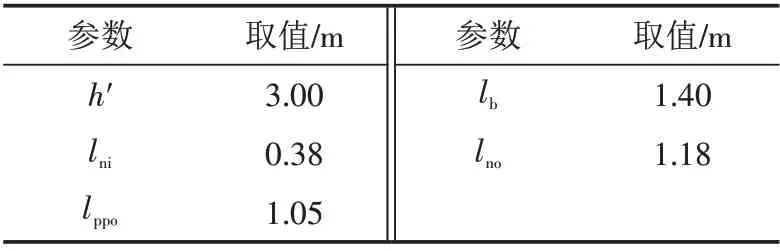
表3 上拉悬挑式支撑体系计算参数Tab.3 Calculation parameters for pull-up cantilever support system

按照式（27）计算得出的悬挑主梁弯矩图和有限元计算得出的弯矩图对比如图7所示. 按照式（30）计算得出的挠度和有限元计算得出的挠度分别为1.61 mm 和1.78 mm. 弯矩对比和挠度对比可以看出，解析公式计算的内力和变形均与有限元法计算结果差别较小，这直接表明了解析公式具有较高的计算精度.

图7 有限元和理论计算结果对比Fig.7 Comparison of finite element and theoretical calculation results

2.4 三种支撑体系受力对比分析

考虑到悬挑主梁是三种支撑体系所共有的构件，而且该构件主要是抗弯构件，因此重点对三种支撑体系下悬挑主梁的弯矩进行对比，对比结果如图8 所示. 从图中可以明显看出，与完全悬挑式主梁相比，下撑悬挑主梁和上拉悬挑主梁的弯矩沿梁轴向的分布更为合理，相应的主梁的承载能力发挥程度沿梁轴向更加均衡. 而且下撑悬挑主梁比上拉悬挑主梁的材料承载能力发挥沿梁轴向更合理. 由此可以看出，下撑梁和上拉杆的存在会使悬挑主梁的材料强度利用率得到明显提高，而且下撑梁使悬挑主梁材料强度利用率的提高更为明显. 这主要是因为下撑梁的刚度要明显大于上拉杆的刚度，因此其对悬挑主梁的约束作用明显强于上拉杆.

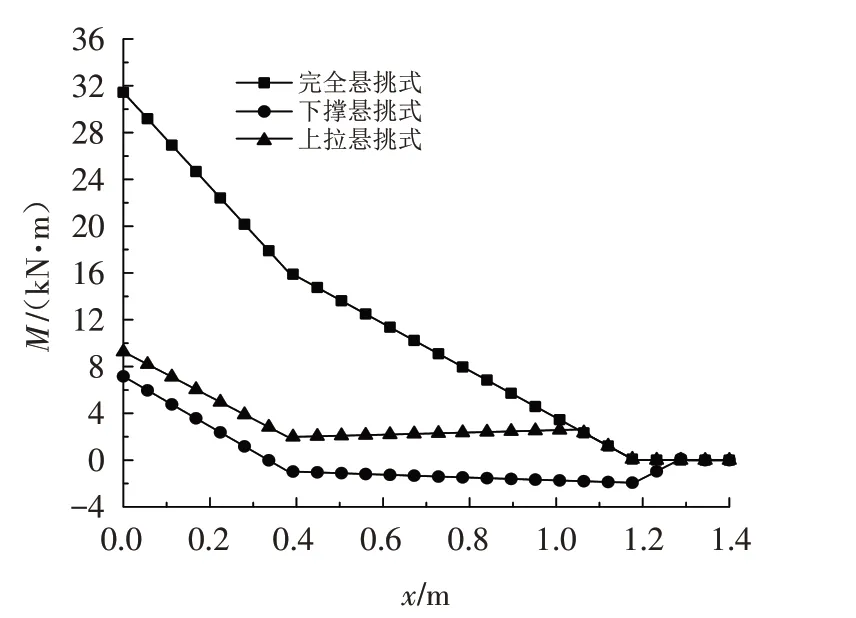
图8 三种支撑体系下悬挑主梁内力对比Fig.8 Comparison of internal forces of cantilever main beam under three support systems

完全悬挑式、下撑悬挑式、上拉悬挑式支撑体系对应的悬挑主梁自由端挠度分别为17.86、0.36、1.61 mm，由此可以看出下撑梁和上拉杆的作用均会使悬挑主梁的变形大大减小，而且下撑梁对主梁的约束作用明显强于上拉杆对主梁的约束作用，在不考虑成本因素的情况下，无论从主梁内力合理性角度，还是从控制主梁变形的角度，下撑悬挑式承载体系无疑是最优的.

3 三种支撑体系的效益对比分析

脚手架主要为现场施工提供平台，其并不直接产生经济效益. 随着建筑行业利润率的持续走低，现场施工管理人员和设计人员总希望在保证施工工期的情况下，尽可能低成本的完成脚手架的搭拆和使用. 考虑到三种脚手架最大的不同在其承载体系，因此重点对三种支撑体系的经济效益、社会效益和施工工期进行对比，对比结果可供施工管理人员和设计人员参考.

经济效益、社会效益和施工工期对比工作是以京No.2017G72地块房地产开发项目4#楼悬挑脚手架设计为例进行的. 在实际设计工作中4#楼采用上拉悬挑式支撑体系，对应的费用如表4所示. 其中，上拉悬挑式支撑体系的费用主要包括主梁、上拉杆、螺栓连接件、技术服务、检测费用、劳务费用等；完全悬挑式支撑体系的费用主要包括主梁、卸荷绳、U形环、技术服务、检测费用、劳务费用等；下撑悬挑式支撑体系的费用主要包括主梁、下撑梁、螺栓连接件、技术服务、检测费用、劳务费用等.

表4 三种支撑体系费用对比表Tab.4 Cost comparison of three support systems

3.1 经济效益对比分析

为对比分析三种支撑体系的经济效益，对完全悬挑式支撑体系的主梁进行选择，对下撑悬挑式支撑体系的主梁和下撑梁进行选择，保证这两种支撑体系对应的主梁的梁端挠度和主梁最大主应力与上拉悬挑式支撑体系对应的主梁挠度和最大主应力相近. 所得出的完全悬挑式支撑体系、下撑悬挑式支撑体系对应的费用同样列于表4中.

从表中的费用对比可以看出，在达到同样的主梁的挠度和正应力控制水平情况下，三种支撑体系费用由高到低为完全悬挑式、下撑悬挑式和上拉悬挑式，而且上拉悬挑式所对应的费用只有完全悬挑式所对应费用的51.07%，即与完全悬挑式支撑体系相比，上拉悬挑式能节约48.93%的费用. 这主要是因为完全悬挑式支撑体系主梁伸入建筑结构内部的部分无法发挥直接的承载作用，而且完全悬挑式支撑体系主梁是完全悬臂构件，其材料利用效率沿主梁长度方向差异很大.

3.2 施工工期对比分析

三种支撑体系的工期对比如表5所示. 从表中可以明显看出，上拉悬挑式支撑体系和下撑悬挑式支撑体系的工期只有完全悬挑式工期的37.5%，这主要是因为上拉悬挑式支撑体系和下撑悬挑式支撑体系以螺栓连接为主，安装

表5 三种支撑体系工期对比表Tab.5 Schedule comparison of three support systems

和拆除速度快，建筑结构上遗留的小洞口只需要注浆封堵即可，施工效率高. 而完全悬挑式撑体系拆除主梁时往往需要切割U形环，而且遗留洞口较大，往往需要混凝土或砌块封堵，施工用时较长.

3.3 社会效益对比分析

与完全悬挑式支撑体系相比，上拉悬挑式支撑体系和下撑悬挑式支撑体系的主梁长度短，截面积小，质量轻，工人施工操作过程中劳动强度更低，施工效率更高.

上拉悬挑式支撑体系和下撑悬挑式支撑体系的材料利用效率更高，符合国家节约资源能源的政策需求.此外，上拉悬挑式支撑体系和下撑悬挑式支撑体系主要以冷作业为主，符合安全文明施工的政策导向需求.

与上拉悬挑式支撑体系和下撑悬挑式支撑体系相比，完全悬挑式支撑体系在结构上预留洞口大，封堵难度大，极易造成外墙渗漏风险，直接影响业主的居住体验，造成后期维修成本的增加.

4 结论

综合采用理论分析法和有限元数值分析方法对完全悬挑式脚手架、下撑悬挑式脚手架和上拉悬挑式脚手架支撑体系进行了构造对比、受力机理对比、效益对比分析. 主要得出如下结论：

1）所提出的三种脚手架支撑体系的内力和挠度计算公式均具有较高的精度，可供具体设计工作参考.2）从主梁内力分布均匀性和控制主梁变形的角度看，下撑悬挑式承载体系是三种体系中最优的，其次为上拉悬挑式支撑体系，最差为完全悬挑式支撑体系.

3）三种支撑体系对应的主梁的梁端挠度相同、主梁最大主应力相同的情况下，与完全悬挑式支撑体系相比，上拉悬挑式能节约48.93%的费用，节省62.5%的工期，而且社会效益好，建议可以在工程实践中重点加以推广.