Multi-Cluster Feature Selection Based on Isometric Mapping
2022-01-26YadiWangZefengZhangandYinghaoLin
Yadi Wang,Zefeng Zhang,and Yinghao Lin
Dear editor,
This letter presents an unsupervised feature selection method based on machine learning.Feature selection is an important component of artificial intelligence,machine learning,which can effectively solve the curse of dimensionality problem.Since most of the labeled data is expensive to obtain,this paper focuses on the unsupervised feature selection method.The distance metric of traditional unsupervised feature selection algorithms is usually based on Euclidean distance,and it is maybe unreasonable to map high-dimensional data into low dimensional space by using Euclidean distance.Inspired by this,this paper combines manifold learning to improve the multi-cluster unsupervised feature selection algorithm.By using geodesic distance,we propose a multi-cluster feature selection based on isometric mapping (MCFS-I) algorithm to perform unsupervised feature selection adaptively for multiple clusters.Experimental results show that the proposed method consistently improves the clustering performance compared to the existing competing methods.
Related work:With the rapid development of data and knowledge management technologies,the amount of data collected in various application areas is growing exponentially.Feature selection method[1] is conducive to reduce dimensionality,remove irrelevant data,and improve resultant learning accuracy of the high-dimensional data.In most of the tasks,the labeled data is often difficult to obtain,which increases the difficulty of the feature selection task.Unsupervised feature selection can be used to process the data without labels which make it better for the distance-based clustering tasks.
The feature selection algorithm could be categorized into three types: filter [2],[3],wrapper [4],and embedded [5].The filter methods first pretreated the data and then throws the processed data into the model for training.The wrapper methods are to continuously optimize the selection by the feedback of the subsequent model.Embedded methods select a feature subset in the learning stage.According to whether or not the label assist feature selection process,the feature selection algorithms can be divided into supervised feature selection [2]–[5] and unsupervised feature selection [6],[7],heuristic-based feature selection exploration is also a very important direction in the feature selection.
The unsupervised feature selection algorithm multi-cluster feature selection (MCFS) [7] could preserve the multi-cluster structure of the data to make it beneficial to multi-cluster tasks.The MCFS algorithm is an unsupervised feature selection algorithm based on manifold learning.It first uses Laplacian Eigenmaps (LE) [8] algorithm to embed the high dimensional manifold data into low-dimensional space,and then process the embedded feature matrix.The LE algorithm uses the Euclidean distance to establish ap-nearest neighbor map.The geodesic distance is the shortest distance that two points on the hypersurface travel along the surface of the hypersurface in high-dimensional space.In dealing with the hypersurface in high dimensional space,when the hypersurface close to the plane,the distance between two points in the low dimensional space approximate the Euclidean distance.When the highdimensional space hypersur face bend degree is large,the geodesic distance can preserve the global structure commendably [9].By introducing the geodesic distance into MCFS,this paper proposes a novel algorithm called multi-cluster feature selection based on isometric mapping (MCFS-I).
Multi-cluster feature selection based on isometric mapping:
1) Manifold data embedding:Manifold data refers to hypersurfaces composed of data in a high-dimensional space.Due to the high dimensional space where these data is located has redundant information,manifold learning [10] is to expand manifold data in high-dimensional space and embed them into low-dimensional subspace.Most manifold learning algorithms use Euclidean distance to establishp-nearest neighbor map to process data,which can only preserve the data in the local manifold structure embedded into low dimensional subspace,and isometric mapping (IsoMap) [9] based on the geodesic distance can well preserve the global structure of the data.
Firstly,IsoMap applies property that the manifold data is locally homeomorphic to Euclidean space.By calculating the Euclidean distance of all data points,its adjacent points can be obtained.After that,each point is connected to its adjacent points,and the geodesic distance between two points is their shortest path in thep-nearest neighbor graph.In this way,the classical shortest path algorithm Dijkstra or Floyd algorithm can be used to approximate the real geodesic distance with the shortest path.Therefore,the global structure of the manifold data can be well preserved,and the global structure can be retained to the maximum extent after the data is embedded in the low-dimensional space.After the distance between any two points is obtained,the multiple dimensional scaling (MDS)algorithms [11] can be used to calculate the coordinates of each data point in the low-dimensional space.The process of IsoMap is shown in Algorithm 1.

2) Learn the sparse coefficient vector:The MCFS-I algorithm is composed of IsoMap algorithm and Lasso regression,the feature matrix is embedded into the low-dimensional space based on geodesic distance and MDS algorithm.Since the dimensions in the low-dimensional space are usually equal to the cluster number,each dimension in the low-dimensional space corresponds to each clustering structure.Based on this,Lasso regression is used to fit the embedding matrix.
When the embedding matrixY∈RN×Kis obtainedby the I so Map algorithm,the feature matrixX∈RN×Mshould benor malizedto make the various feature metric in the feature matrix consistent.A sparse coefficient vector is obtained by fitting each columnykofYwith Lasso regression [12] :
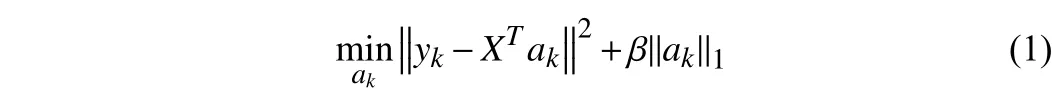
whereakis theM-dimension coefficient vector.Due to the punitive ofL1regularization,whenβis large enough,some coefficients will be reduced to 0 precisely.Since the sparsity of Lasso regression,a sparse matrix will be automatically obtained in the process of solving Lasso regression.Because the metric of features is unified before Lasso regression,the larger the coefficients of some features are,the greater their contribution to resolving cluster structure will be.Moreover,the combination of several features with relatively weak influence can better distinguish different clusters,this property will be ignored when evaluating these features individually.Lasso regression is a combination solution of various features rather than the independent evaluation of features.Therefore,we chose Lasso regression instead of evaluating the contribution of each feature individually.The equivalent form of Lasso regression can be expressed as follows:
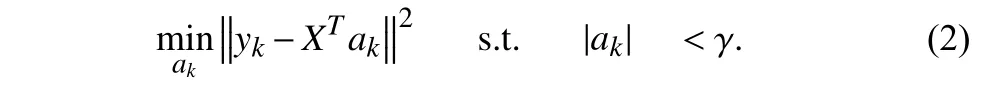
It is difficult to control the sparsity of coefficient matrix precisely in Lasso Regression,while the least angel regression (LARs) [13]algorithm can solve (2) effectively by entering the number of nonzero items inak,the sparsity of coefficient matrix can be easily controlled.Hence,we use LARs algorithm to solve (2).
3) Unsupervised feature selection:By combining IsoMap algorithm and Lasso regression,MCFS-I algorithm embedded the feature matrix of the data into the low-dimensional space according to the geodesic distance,and obtains the low-dimensional representation of the clustering structure.The importance of features is comprehensively measured by Lasso regression,and then thedfeatures with the highest score can be selected by scoring the results of Lasso regression.
Ksparse coefficient vectorsak∈RM,k∈{1,2,...,K} can be obtained by Lasso regression in Section II-B,eachakcorresponds to a cluster,and each item inakrepresents a feature.Since the data is normalized first,the largerak,jis,the greater contribution of thejfeature to thekcluster.Since each feature contributes differently to different clustering structures,it is natural to choose its maximum contribution value as the selection criterion for each feature,which is recorded as MCFS score [7] and it can be defined as follows:
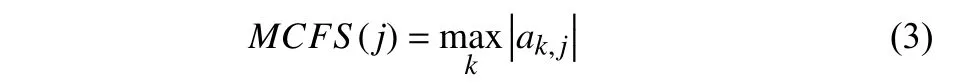
whereak,jis thejelement ofak.After that,the MCFS scores of all features are ranked in descending order,anddfeatures with the largest MCFS score will be selected as the output result of the MCFS-I algorithm.The detailed process of the MCFS-I algorithm is shown in Algorithm 2.

Experiments:In this section,we will evaluate the performance of the MCFS-I algorithm in clustering tasks.We compared the following four algorithms:
● For the proposed MCFS-I algorithm,the nearest neighbors parametern_neighboris set to 5,and the dimension of the embedding matrixn_embis set to be the same as the number of clusters on the data set [14].
● MCFS algorithm [7] uses LE [8] algorithm to process manifold data.
● Laplacian (Lap_score) algorithm [6] selects the data that preserves the local manifold structure.
● Nonnegative discriminative feature selection (NDFS) algorithm[15] combines spectral clustering with the unsupervised feature selection process.
1) Data sets: We selected four commonly used benchmark data sets to test the algorithm separately,which are from scikit-learn and scikit-feature.The detailed information of these data sets is shown in Table 1.
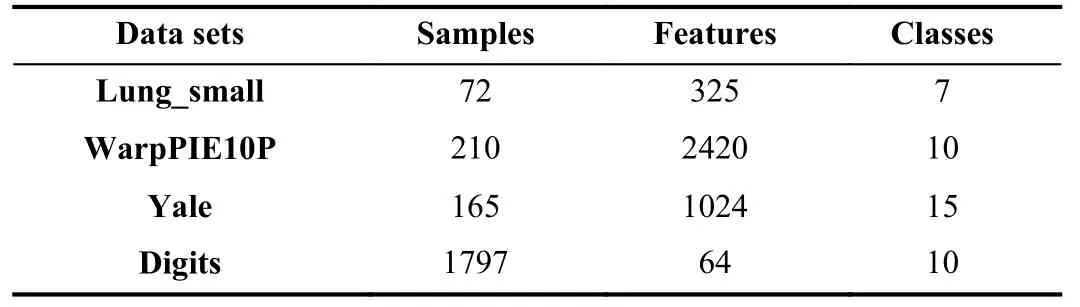
Table 1.Data Sets Used in the Experiment
2) Performance comparisons:In our experiment,we use normalized mutual information (NMI) [6] to evaluate the clustering result on the data which are processed by feature selection algorithm.In each test,we repeat the experiments for five times.Each time we run the k-means clustering algorithm with a random starting point and evaluate it with the NMI evaluation metric.The average NMI value of the five algorithms is used as the comparison results.
The comparison of feature selection results is shown in Fig.1.It can be seen that the clustering performance of the MCFS-I algorithm on each data set is better than the MCFS algorithm,and the clustering result of the MCFS-I algorithm gradually reaches the optimal when the number of features is 50 to 100 on the Lung_small data set.
Table 2 shows the clustering results of each feature selection algorithm when the number of selected features is 100/30 (digits).The column of the “All Features” in the table indicates the performance of the k-means algorithm over the original datasets without using feature selection algorithm.It can be seen that the MCFS-I algorithm has shown the best performance on all data sets,and the MCFS-I algorithm performs better than that when all features are used on some of these data sets.The average improvement of the MCFS-I algorithm over the MCFS algorithm on the four data sets is about 3.206%,the average improvement for the Lap_score algorithm is about 14.822%,and the average improvement for the NDFS algorithm is about 7.704%.
It can be observed from Table 2 that the MCFS-I algorithm on the biological data set has a greater improvement than the MCFS algorithm,while the improvement on the other three image recognition data sets is small.This is because biological data sets have higher requirements for global information,while image data pays more attention to local information.

Table 2.The NMI of the Feature Selection Algorithms (%)
Conclusions:This paper proposes a multi-cluster feature selection based on isometric mapping (MCFS-I) algorithm by introducing the geodesic distance into MCFS.The proposed algorithm uses IsoMap to capture global information and embed it into a low-dimensional space,which is extremely beneficial to process the data with global information.In the experimental section,we compare MCFS-I with MCFS and two commonly used unsupervised feature selection algorithms Laplacian score and NDFS on four benchmark data sets,and the experimental results demonstrate the superiority of the proposed algorithm.
Acknowledgments:This work was supported by grants from the National Natural Science Foundation of China (62106066),Key Research Projects of Henan Higher Education Institutions(22A520019),Scientific and Technological Project of Henan Province (202102110121),Science and Technology Development Project of Kaifeng City (2002001).
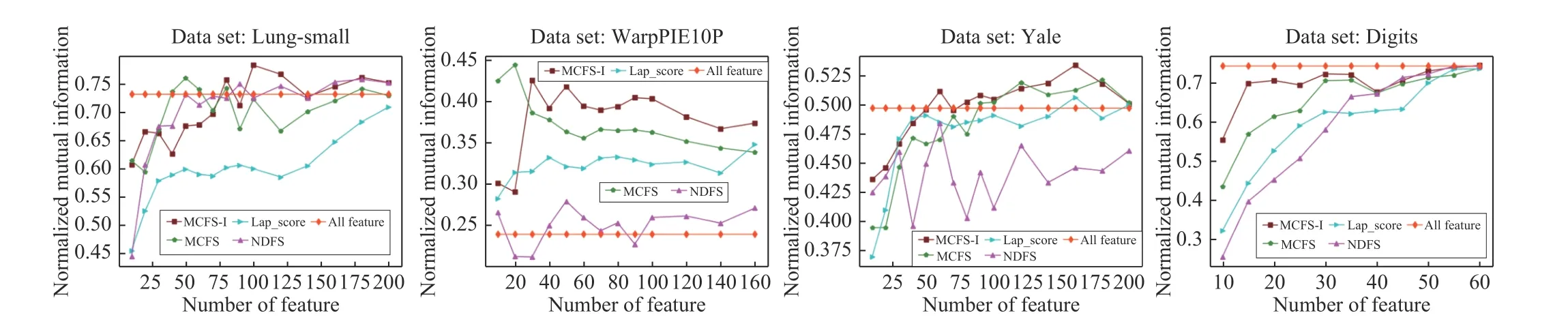
Fig.1.NMI of the different feature selection algorithms on four data sets.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Deep Learning Based Attack Detection for Cyber-Physical System Cybersecurity: A Survey
- Sliding Mode Control in Power Converters and Drives: A Review
- Cyber Security Intrusion Detection for Agriculture 4.0: Machine Learning-Based Solutions,Datasets,and Future Directions
- Barrier-Certified Learning-Enabled Safe Control Design for Systems Operating in Uncertain Environments
- Cubature Kalman Filter Under Minimum Error Entropy With Fiducial Points for INS/GPS Integration
- Conflict-Aware Safe Reinforcement Learning:A Meta-Cognitive Learning Framework
