Sliding Mode Control in Power Converters and Drives: A Review

Ligang Wu,,Jianxing Liu,,Sergio Vazquez,,and Sudip K.Mazumder,

Abstract—Sliding mode control (SMC) has been studied since the 1950s and widely used in practical applications due to its insensitivity to matched disturbances.The aim of this paper is to present a review of SMC describing the key developments and examining the new trends and challenges for its application to power electronic systems.The fundamental theory of SMC is briefly reviewed and the key technical problems associated with the implementation of SMC to power converters and drives,such chattering phenomenon and variable switching frequency,are discussed and analyzed.The recent developments in SMC systems,future challenges and perspectives of SMC for power converters are discussed.

NOMENCLATURE

VoOutput voltage of the dc/dc power converter

VinInput voltage of the dc/dc power converter

iLInductor current of the dc/dc power converter

vdcOutput voltage of grid-connected power converter

vabcAC voltage vector inabcframe

vαβAC voltage vector in α β frame

vdqAC voltage vector indqframe

iabcAC current vector inabcframe

iαβAC current vector in α β frame

idqAC current vector indqsynchronous frame

idqAC current vector indqsynchronous frame

p,qActive power and reactive power

CDC-link capacitor

LLine inductor

RLLoad resistance

ωRotor speed

TElectromagnetic torque

Ψ Rotor flux

I.INTRODUCTION

SLIDING mode control (SMC) is a special kind of nonlinear control which has proven to be an effective robust control strategy for incompletely modeled or nonlinear systems since its first appearance in the 1950s [1]–[4].One of the most distinguished properties of SMC is that it utilizes a discontinuous control action which switches between two distinctively different system structures such that a new type of system motion,called sliding mode,exists in a specified manifold.This peculiar characteristic of the motion in the manifold provides insensitivity to the matched disturbances.In order to deal with the unmatched uncertainties,SMC with other approaches such as adaptive approach [5],LMI-based approach [6] and observer based approach [7],etc.,have been proposed in many works [8],[9].

SMC has been applied primarily to the control of variable structure systems,its analysis and design are well presented in books,survey and tutorial papers [10]–[17],both from a theoretical and implementation perspective.In general,SMC suffers from the so-called chattering phenomena,which is undesirable because it often causes control inaccuracy,high heat loss in electric circuitry,and high wear of moving mechanical parts [18]–[20].In addition,the chattering action may excite the unmodeled high-order dynamics,which could damage actuators,systems and even leads to unforeseen instability.The chattering in SMC systems is usually caused by

· Utilization of digital controllers with the finite sampling rate,which causes the so-called discretization chattering.Theoretically,the ideal sliding mode implies infinite switching frequency.Since the conventional SMC action is constant within a sampling interval,the switching frequency can not exceed that of half the sampling frequency,which leads to chattering.

· The unmodeled dynamics with small time constants,which are often neglected in the ideal model.

Whatever the case may be,a high switching frequency is not feasible or undesirable for practical power electronics applications due to limitations of switching devices,such as losses,time delay,response time constant,the presence of dead zone,hysteresis and saturation of device switching frequency [21].

Despite the chattering phenomena,the inherent switching nature of SMC is quite suitable and even advantageous for power converters due to its switched operation.Therefore,SMC is an interesting solution to deal with power electronics systems,such as switching dc/dc power converters,gridconnected power converters,and motor drives.

During the last few years,power electronics has undergone an intense technological evolution through the advancements of the power semiconductor industry.For example,the new generation of semiconductor switches operates with faster switching frequency and handles higher powers than the previous one.The widely used real-time computer controllers make the implementation of advanced and complex control algorithms a reality.These factors together have led to the development of cost-effective and grid-friendly converters,which play the fundamental roles in applications such as renewable energy sources and their integration into the electrical grid,motor drives,etc [22]–[25].

This paper is focused on the application of SMC for power converters and drives.The basic SMC theory is revisited and the particular problems and solutions,when applied to power electronics systems,are discussed and analyzed.Methods for solving major challenges of conventional SMC such as chattering phenomenon and variable switching frequency are addressed,and new trends and challenges for its application to power electronic systems are examined.

This paper is organized as follows: Section II briefs the fundamental theory and methodologies of SMC.The use of SMC for different types of power electronics systems are presented in Sections III to V.Future challenges to adopt SMC as an industry solution to power converters are addressed in Section VI.Finally,Section VII concludes the paper.

II.SMC FUNDAMENTAL THEORY AND METHODOLOGIES

SMC has been recognized as an efficient tool to design robust controllers for complex high order nonlinear dynamic plants operating under various uncertainty conditions since its first appearance in the 1950s.The major advantage of the sliding mode is the low sensitivity to plant parameter variations and external disturbances which relaxes the necessity of exact modeling.SMC enables the decoupling of the overall system motion into independent partial components of lower dimension,which reduces the complexity of feedback design.SMC has been developed as a new control design method for a wide spectrum of systems including nonlinear,time-varying,discrete,large-scale,infinite-dimensional,stochastic,and distributed systems [26].Also,in the past two decades,SMC has successfully been applied to a wide variety of practical systems such as robot manipulators,aircrafts,underwater vehicles,spacecrafts,flexible space structures,power electronics,control of electric drives,doubly fed induction generator,robotics,and automotive engines [10],[27]–[29].

In this section,the basic notion of SMC,the controller design principle and their distinguishing features are presented.

A.Fundamental Theory of SMC

Let us consider the following nonlinear system:

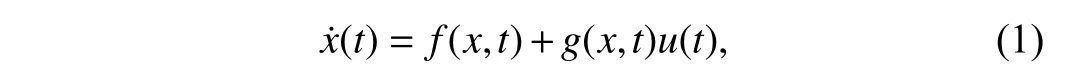
wherex(t)∈Rnis the state variable vector,u(t)∈Rmis the control input,f(·,·) andg(·,·) are continuous functions inxandtvector fields [10],[30].Note that thenis the dimension of the state variable vectorx(t),and themis the dimension of the control input vectoru(t).

The sliding mode controller

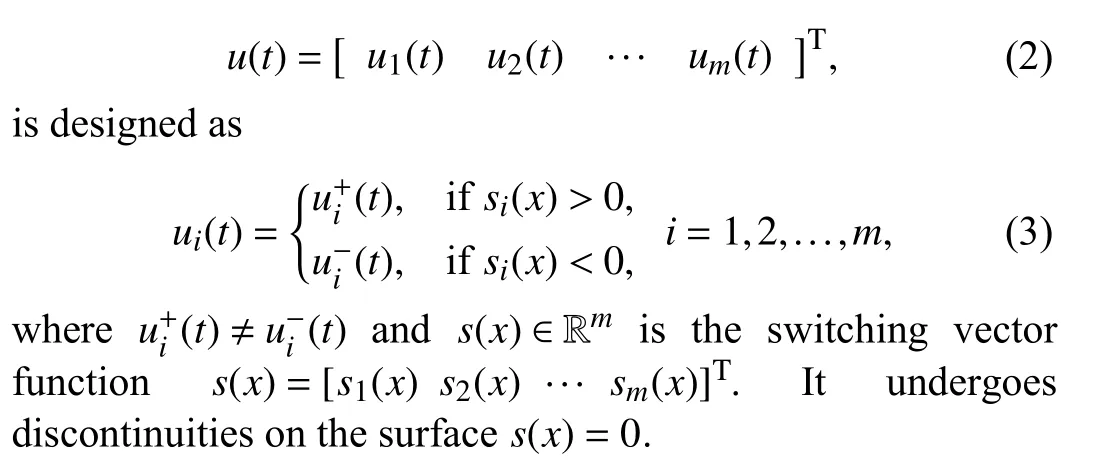
Note that SMC law (3) is designed to ensure that the sliding surface (s(x)=0) is reached and then motion on the sliding surface is maintained.This means that the so-called‘reachability condition’ should be satisfied by manipulating the control lawu(t).The sufficient condition for the system(1) to satisfy the reachability condition is expressed as

Condition (4) guarantees that the trajectory of the system states always points towards the sliding surface.A more strict reachability condition called ‘η-condition’ is given as follows

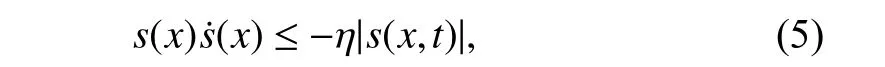
whereηis a positive scalar.Condition (5) ensures that the sliding surface is reached in finite time.

B.SMC Design Methods

Several SMC design methods have been proposed in literature which mainly consist of two steps [10],[30]:

Step 1:Design a sliding manifolds(x) which provides desired performance in the sliding mode,such as stability,disturbance rejection capability and tracking;

Step 2:Design a discontinuous feedback controlu(t) which will force the system states to reach the sliding manifold in finite time,thus the desired performance is attained and maintained.

For ease of implementation,the sliding variablesi(x),i=1,2,...,mis chosen as a linear combination of the state variables,expressed as

where αjidenotes the sliding coefficients andxj(t)∈x(t).The main objective of the sliding mode controller is to drive the system state trajectories onto the specified sliding surface in a finite time and maintained there for all subsequent time.Typical SMC strategies will be introduced in the following.

1) Equivalent control-based design:For the system (1),assuming that the termis non-singular,the control lawu(t) is designed as follows,

whereueq(t) represents a continuous component anduN(t)represents a discontinuous component.

The equivalent controlueq(t) is derived from the so-calledequivalent control method,i.e.,in the case whens(x)=s˙(x)=0.Thus,ueq(t) is calculated as

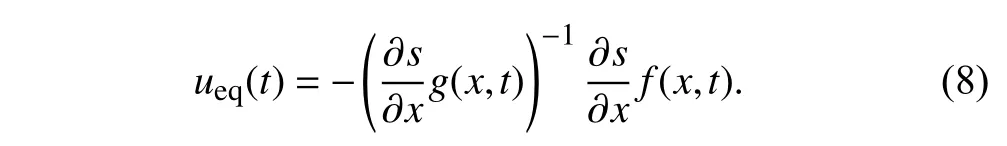
Substituting the above equivalent control (8) into the original system (1),it follows that the motion of sliding mode is determined by

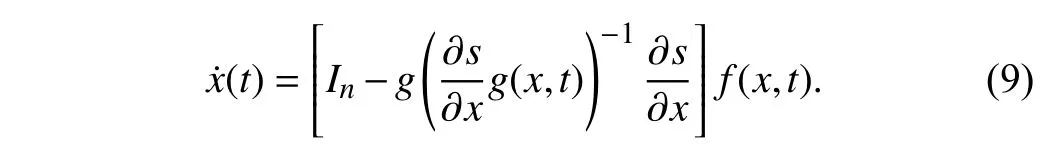
where (9) is considered as the equation of the sliding mode in the manifolds(x)=0.

The high frequency switching actionuN(t) is designed as

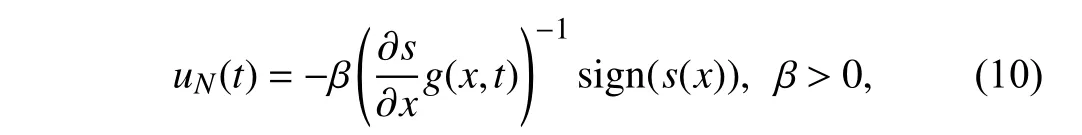
such that the derivative of the Lyapunov functionis negative,that is

Remark 1:The physical meaning of the equivalent control can be interpreted as the low-frequency component of the discontinuous control lawu(t),because the high-frequencyuN(t)can be filtered out by a low pass filter of the system

which meansz≃ueq.

2) Reaching law approach:The reaching law specifies the dynamics of a switching function,which can be described by the following differential equation:

and Υ=diag{ε1,ε2,...,εm},εi＞0,K=diag{k1,k2,...,km},ki＞0,gi(0)=0,si(x)gi(si(x))＞0,i=1,...,m.

Equation (13) is only a general form of reaching law.In fact,there are many reaching laws and some special cases are

1) The constant rate reaching law:

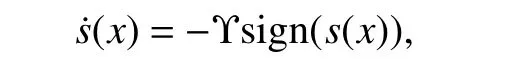
2) The constant plus proportional rate reaching law:

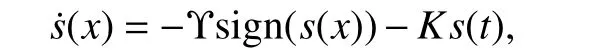
3) The power rate reaching law:

The reaching law approach not only guarantees the reaching condition but also specifies the dynamic characteristics of the motion during the reaching phase.

C.Chattering Phenomenon

Chattering problem is one of the main obstacles for applying SMC to real applications.It is caused by unmodeled dynamics or discrete time implementation.Chattering leads to undesirable results,such as low control accuracy,high heat loss in electric circuitry,and high wear of moving mechanical parts [31].In addition,it may excite the unmodeled high-order dynamics,which probably leads to unforeseen instability.Therefore,various methods have been proposed in literature to reduce or soften the chattering action [32]–[36].Among others,the main approaches to avoid or limit the chattering problems are shown in Table I.It should be noted that in addition to these methods mentioned in Table I,fractionalorder SMC [37] and disturbance observer based SMC approaches [7] are also common and typical approaches to soften the chattering problem.

III.SMC STRATEGIES OF DC/DC POWER CONVERTERS

SMC is naturally well suited for the control of variable structure systems.Since power converters inherently include switching devices,they belong to variable structure systems.Therefore,it is straightforward to apply SMC that yields a discontinuous control law [10].Moreover,given that power converters are usually modeled using the state space averaging method,SMC forms an efficient analysis and design tool for the control of switched mode power converters because it offers excellent large-signal handling capability.

Conventional linear control is small signal based.It only allows one to optimally operate the converters for a specific range of operating conditions and often fails to achieve satisfactory performance under large parameter/load variations,i.e.,large-signal operating condition.SMC as a kind of nonlinear control method.It is suitable for controlling the power converters,which is able to achieve better regulation and dynamical performance for a wider range of operating conditions.The main reason is that there’s no need to have a linear model of the power converter for nonlinear controller design.However,the main obstacle associated with the application of SMC is its variable frequency nature,which makes the design of output filter difficult.Nonetheless,if this problem is properly handled,SMC is a powerful control design method for power converters and has a huge potentialin industrial applications [21].

TABLE IMAIN APPROACHES TO ALLEVIATE OR LIMIT THE CHATTERING PROBLEMS

Many sliding-based controllers have been proposed for dc/dc converters,such as SMC based on Hysteresis-Modulation (HM) technique or fixed-frequency SMC[52]–[54].As it is well known,the direct implementation of SMC will result in some high and uncontrolled switching frequency which makes them unsuitable for industrial applications.HM-based SMC is adopted to limit the operating frequency via tuning the hysteresis parameter.It should be noted that the operating frequency is only limited but it is still variable [21].

Generally,there are three approaches to make the switching frequency constant.The first approach is to incorporate a constant ramp or timing function directly into the controller[55].The second approach is to apply the adaptive hysteresis concept,with a hysteresis level which can be varied with both input and output voltages to force the switching frequency to remain a constant under all load conditions [50].The thirdapproach is to achieve constant switching frequency by employing PWM technique.The PWM-based SMC can be obtained by translating the equivalent controlueqto the duty ratio of the PWM,d.The equivalent control signalueqis calculated by setting the derivative of the sliding variable to zero,i.e,s˙=0.The control signaluis compared to the PWM carrier to generate a discrete gate pulse signal.

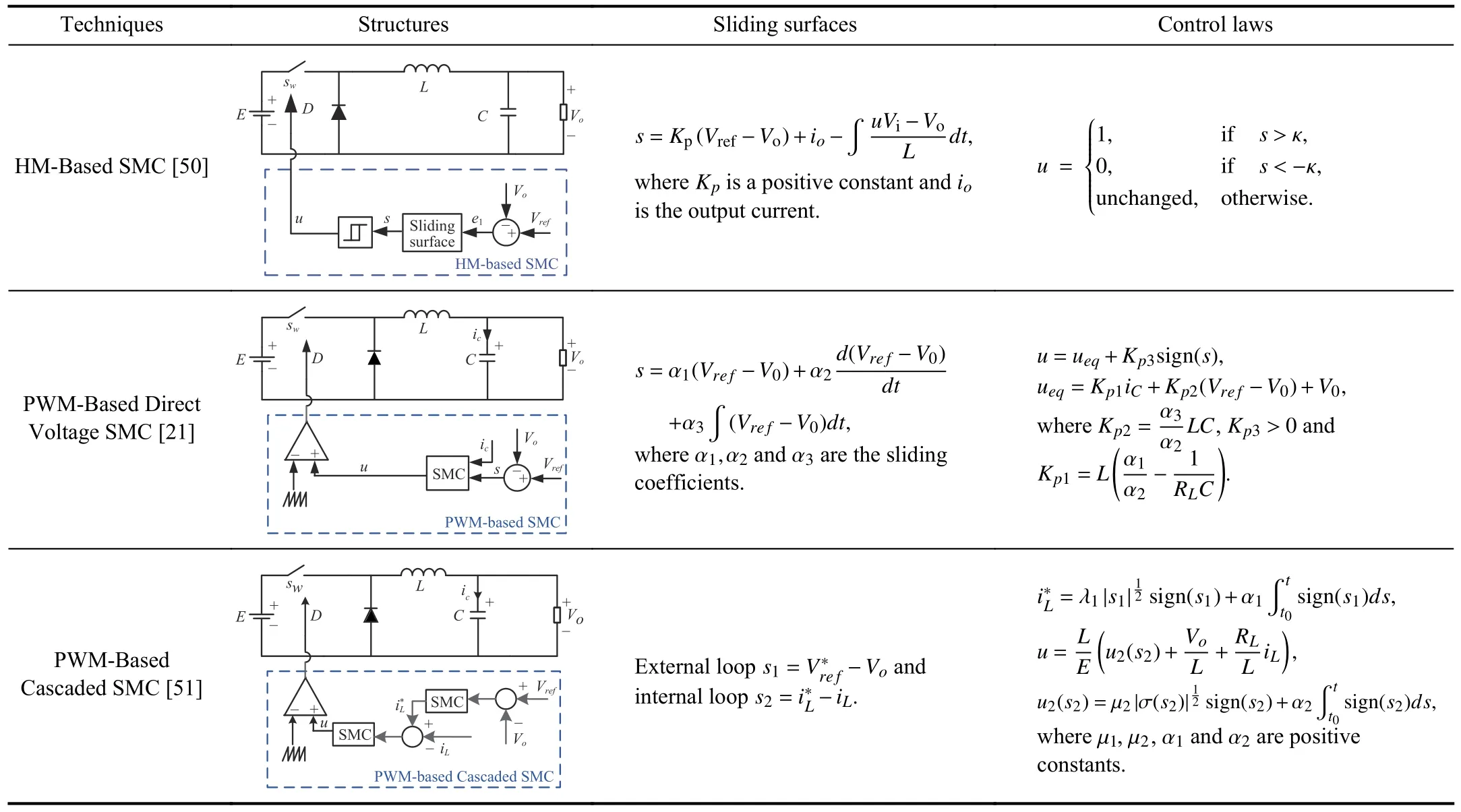
TABLE IISMC STRATEGIES FOR BUCK CONVERTER

Mazumderet al.proposed a first fixed-frequency PWMbased integral variable structure sliding mode controller for parallel buck converters [53].This technique was subsequently extended for control of the voltage regulator module application in [56].Later,a unified fixed-frequency PWM-based direct sliding mode voltage control design was proposed for the buck,boost and buck-boost converters [57].Its main disadvantage is that it lacks robustness against system parameters,i.e.,load resistance and capacitors.Pointed out by[12] that direct sliding mode voltage control for boost and buck/boost converters may result in the instability of the system.Cascade control structure which consists of an inner current loop and outer voltage loop is introduced to solve this problem.This control method increases the overall system’s stability (phase) margin,and hence simplifies the design of the outer voltage loop.It can be concluded from [58] that sliding mode current controller may be a good alternative over conventional current-mode controllers for fast-response boost converter applications but at a higher implementation cost and circuit complexity.

As an illustrative example,three SMC strategies for buck converter are presented in the discussion.The mathematical model of the typical buck converter can be expressed as,

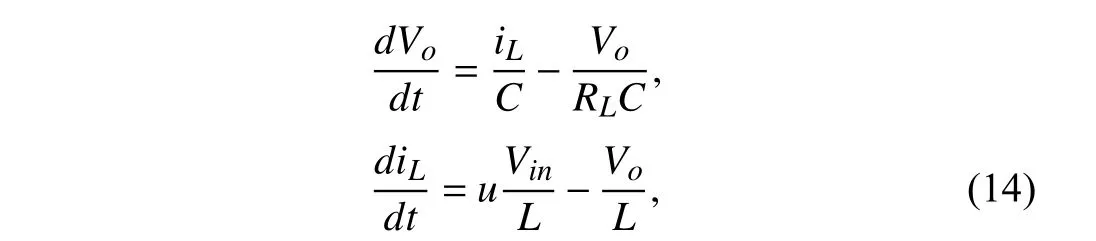
whereL,CandRLrepresent inductor,storage capacitor and load resistance,respectively;iL,VinandVoare inductor current,input voltage and output voltage,respectively.

However,these strategies are generally applicable to any dc/dc converter types.Basic structures of typical HM-based SMC,fixed-frequency PWM based SMC and cascade control structure for a dc/dc converter system are shown in Table II.

A.SMC Based on HM Technique

The schematic diagram of the buck converter with an HMbased SMC is shown in Table II.The sliding surfacesis defined as

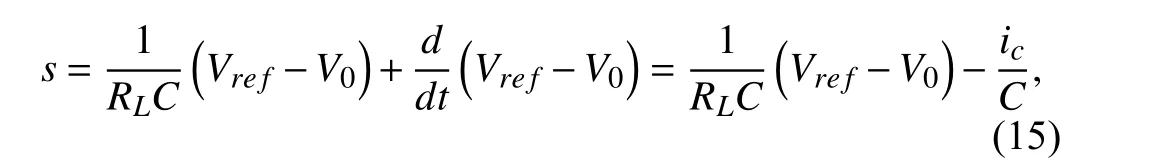
whereCandRLare the capacitance,and instantaneous load resistance,respectively.VrefandV0are the desired and capacitor output voltage,respectively.

To drive the trajectories onto the sliding surfaces=0,the control lawucan be designed as:

whereu=1 corresponds to the conducting state of the switching elementsωwhileu=0 corresponds to nonconducting state of the switching elementsω.

Remark 2:It is worth noting that,in the ideal sliding mode,the state trajectories are directed towards the sliding surface at an infinite switching frequency.However,practical applications limit the switching frequency to reduce the power losses in the converter.A hysteresis band with the boundary conditionss=κ ands=-κ is introduced to deal with this problem.The control law in (16) is redefined as

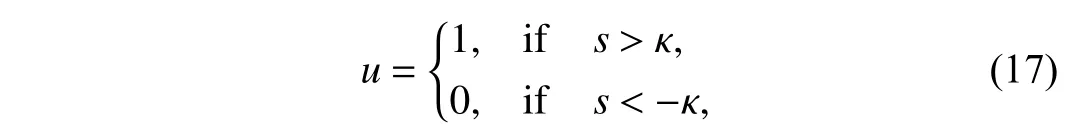
where κ is an arbitrarily small value.

The introduction of hysteresis band only solves the problem of high switching losses,however,variable switching frequency still exists.PWM techniques are employed to achieve constant switching frequency SMC.

B.Fixed-frequency PWM Based SMC

The schematic diagram of the buck converter with a fixedfrequency PWM-based SMC is presented in Table II.The main idea is to use a pulse-width modulator that employs an equivalent control signal to be compared with the fixedfrequency ramp in the modulator.The sliding surfacesis defined as,

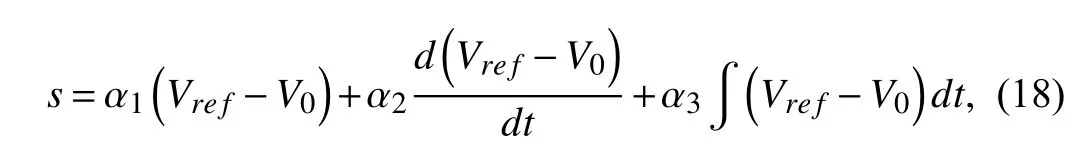
where the positive constants α1,α2and α3are the sliding coefficients [21].Then the control lawucan be designed as:

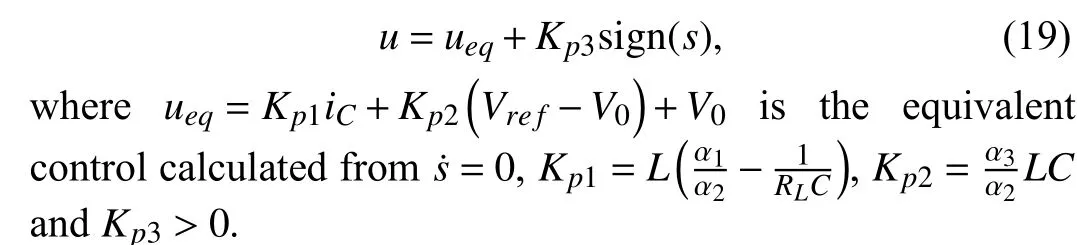
This approach solves the problem of a resulting variable switching frequency but may lead to system instability.

C.Cascade Control Structure

The schematic diagram of the buck converter with a cascade control structure based SMC is presented in Table II.A cascade-control comprises two control loops.The voltage regulation loop is the external loop which provides the current reference for the inner loop [51].The sliding surface is defined as

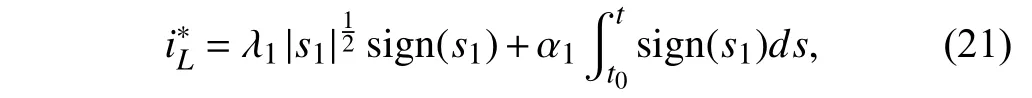
where λ1and α1are positive constants.

The inner loop is focused on the current tracking.In this case,the sliding surface is defined as

and the control lawuin the internal loop can be designed as

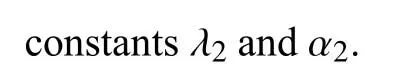
This approach provides fixed switching frequency and offers more robustness compared with direct voltage SMC.The features of different SMC techniques for a dc-dc buck converter are presented in Table III.

IV.SMC FOR GRID-CONNECTED POWER CONVERTERS

With the advent of distributed dc power sources in the energy sector,grid-connected power converter plays a key role in industrial applications like integration of renewable energy sources such as wind power systems or photo-voltaic,energy storage systems,motor drives,battery charger in electric vehicles,etc [59]–[63].PWM converters can operate with a high power factor or any active/reactive power combination.Typically,in the application of renewable energy sources,power converter plays an important role in transforming the renewable energy in electrical energy efficiently and economically.For electric vehicles,power converter works as an interface in the electrical propulsion system turning electrical power to mechanical power for sake of efficiently driving the electric motor.It is also known as the active front end (AFE),which is grid-connected converter that offers features as bidirectional power flow,near-sinusoidal currents,power factor and dc-link capacitor voltage regulation capability [64].The typical AFE is the three-phase two-level grid-connected power converters and its mathematical model indqsynchronous can be described as

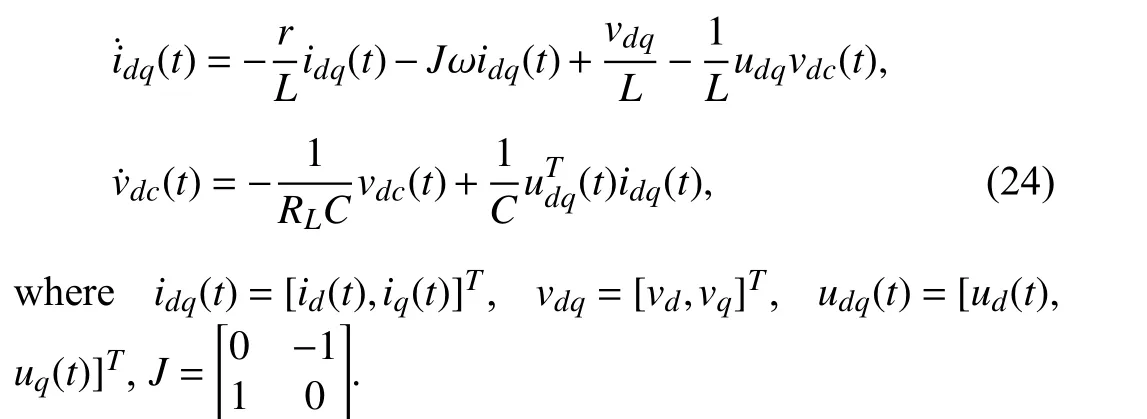
Different generic loads can be connected to the dc-link depending on the direction of the power flow.A resistive load is connected to the dc-link as a rectifier.For grid integration of renewable energies such as wind power,a power converter(rotor side converter) is connected to the dc-link for the torque and/or speed regulation [70].

The main control objectives for AFE are to regulate the dclinkvoltageVdcto a certain referenceforany connected load and supply a desired reactive power and draw grid currents with the lower harmonic distortion.Several control methods have been proposed for the control of power converters [71].In general,a cascade control structure is used which consists of an external control loop and inner control loop.The external control loop is employed to regulate the dclink voltage to some desired value.The inner control loop is designed to force the grid currents or the instantaneous active and reactive power to track their references [72],[73].As discussed in [71],the performance of the converter system largely depends on the quality of the inner control strategy.Since grid-connected power converters are variable structure systems,sliding mode techniques are desirable to tackle their control problems.They are able to ensure stability,robustnessand increase the dynamic response in the presence of parameter uncertainties and external disturbances.The cascade control structure,which includes outer control loop and inner control loop [74],employing SMC for AFE is shown in Fig.1.SMC for grid-connected power converters is summarized in Tables IV and V.

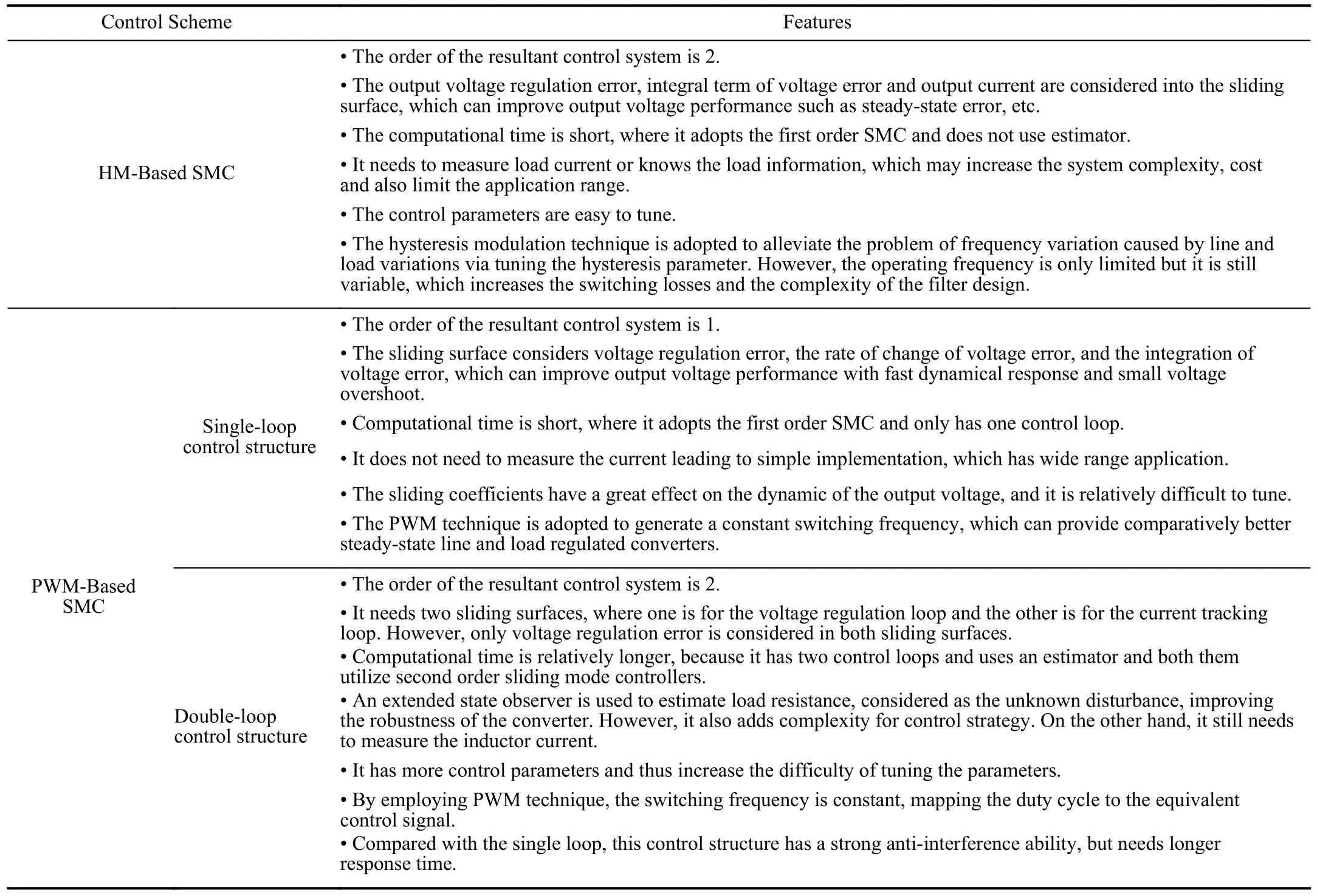
TABLE IIITHE FEATURES OF DIFFERENT SMC TECHNIQUES FOR DC-DC BUCK CONVERTER

Fig.1.Cascade control structure for grid-connected power converters.

Many research endeavors have been focused during the recent years,on control problems in PWM rectifiers.Silva[65] designed a robust sliding-mode controller,suitable for the output voltage control of voltage-sourced unity-power-factor three-phase PWM rectifiers.Through the comparison with PI controller,it shows that the robust sliding-mode controller offers faster dynamics and does not present steady-state errors.Control methods based on state-space average models,using linear regulators for the rectifier output voltage control,must change the modulation index slowly,to ensure stability,thus losing response speed.However,the PI regulator parameters are dependent on the load,system parameters,and on the operating point.Responses,with loads far from the nominal one,are not good enough,presenting rise times and damping factors depending on the load and on the rectifier operating point.Some works have treated the sliding-mode control of these PWM rectifiers just considering the slow and fast manifold approximation [75].Therefore,they control only the input currents in sliding mode and this approach yields robust input current controllers,but non-robust output voltage controllers.Furthermore,their robustness can only be improved using complex control processes.

Pireset al.[76] proposed a cascade sliding mode controller for a three-phase buck-boost-type rectifier.In the inner current loop,a vector-based sliding-mode control method is used to generate (αβ) space-vector modulation,which forces the input line currents to track a suitable sinusoidal reference.In the outer voltage regulation loop,a PI controller is adopted to regulate the output voltage of the converter.In order to guarantee robustness against load variation,a composite control law consisting of super-twisting based SMC and an extended state observer is developed for the voltage regulation loop [66].

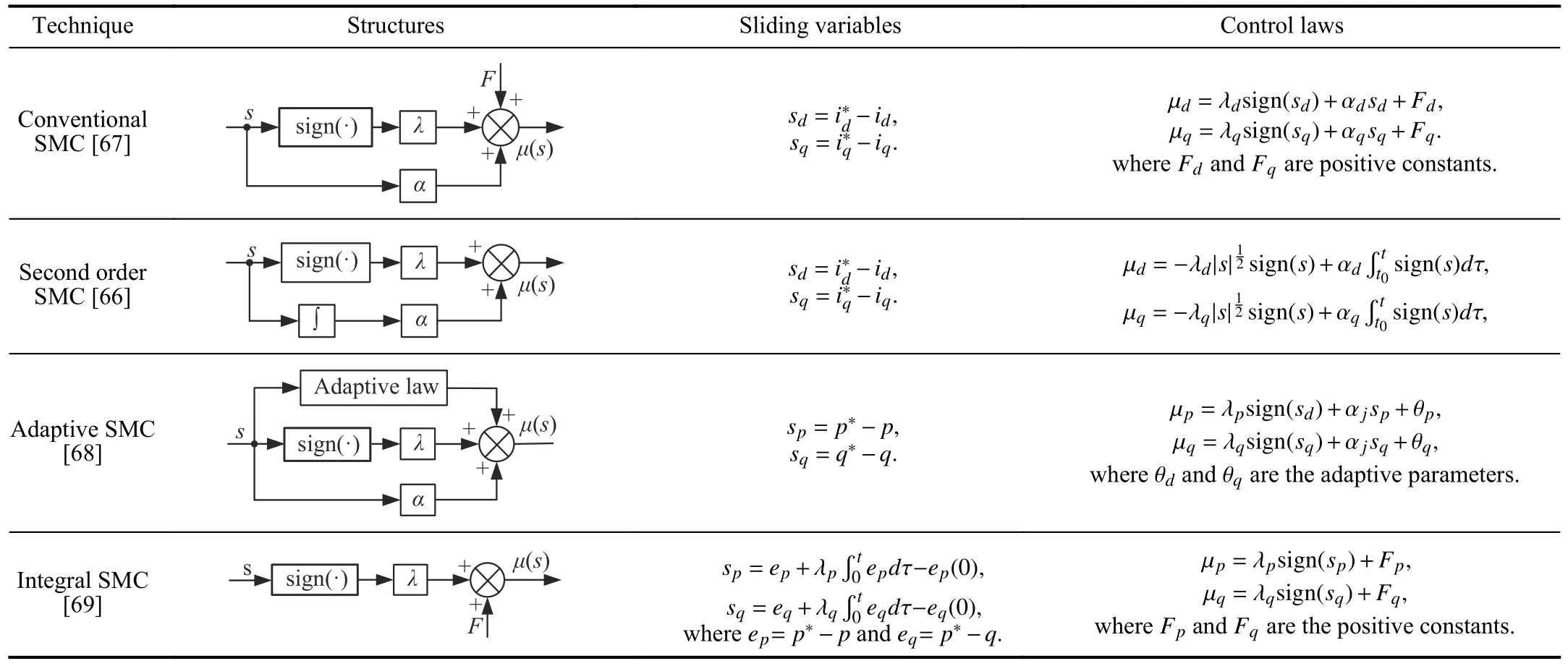
TABLE VSMC FOR GRID-CONNECTED POWER CONVERTERS: INNER CONTROL LOOP

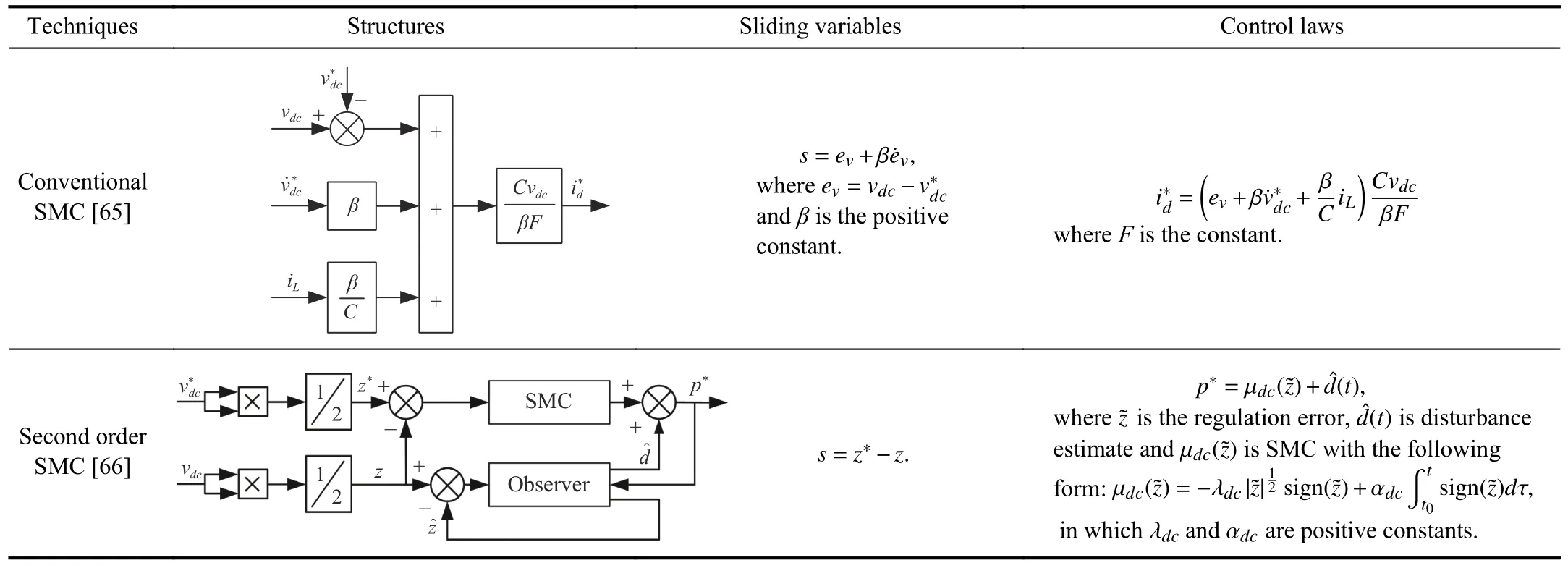
TABLE IVSMC FOR GRID-CONNECTED POWER CONVERTERS: OUTER CONTROL LOOP

While SMC has been extensively researched in the context of standalone PWM rectifiers,pioneering work has been conducted in [77],where SMC has been applied to plurality of PWM rectifiers connected in a parallel configuration to feed a dc bus from power delivered by a ac multiphase power source.In this application,SMC has been integrated with novel spacevector modulation [78] in a three-dimensional synchronous frame to not only alleviate problems associated with circulating currents in non-isolated parallel PWM rectifiers but also achieve constant frequency of operation even while achieving high quality performance while satisfying stability bound.Subsequently,additional SMC was developed in [79].

Most of the above works need continuous measurements of ac voltages,ac currents and dc voltage.This requires a large number of both voltage and current sensors,which increases system’s complexity,cost,space and reduces system reliability.Moreover,the sensors are susceptible to electrical noise,which cannot be avoided during high-power switching.Reducing the number of sensors has a significant effect upon the control system’s performance.In [80],a simple control scheme was presented for the three-phase power converter without using a current sensor,where the current command can be automatically adjusted.By using the information from dc-link current sensor,a technique of reconstructing threephase input currents was given to control three-phase voltagesource converters in [81].Leeet al.[82] proposed a control strategy for three-phase power converter without using any ac input current and voltage sensors in order to achieve desired control performance of the dc output voltage regulation over a wide range.The input phase currents are reconstructed from the switching states of the ac/dc rectifier and the measured dclink currents,and then used in feedback control.The phase angle and the magnitude of the source voltage were estimated by controlling the deviation between the rectifier current and its model current to be zero.However,they require digital sampling of the dc-link current in every switching cycle and numerical computations.The accuracy of measurement is inherently controlled by the sampling rate.

V.SMC FOR HIGH PERFORMANCE MOTOR DRIVES

For the control of the motor drive system,the conventional PI control has been commonly adopted because of its simplicity,strong adaptability and reliability.Nevertheless,PI control may not guarantee that the motor has high performance under parameter and load variations.Thus,a large amount of advanced control methods,such as model predictive control [70],[83],[84],adaptive control [85],[86],fuzzy control [87] and SMC [88]–[90],etc.,have been proposed to improve the performance of the motor.Among these advanced control approaches,SMC can perfectly deal with the disturbances and uncertainties of the motor system causing unmodeled dynamics,friction force,and load disturbances to reach a high performance for motor control.

Fig.2 is a typical cascade control structure employing SMC for the motor drives [91]–[93].Note that the speed observer in the Fig.2 is not mandatory,only for the speed sensor less control strategies.In [92],[93],the continuous fast terminal sliding mode control (CFTSMC) is adopted in the outer control loop to regulate speed of permanent magnet synchronous motor (PMSM),shown in Fig.3.In which the CFTSMC is designed as,

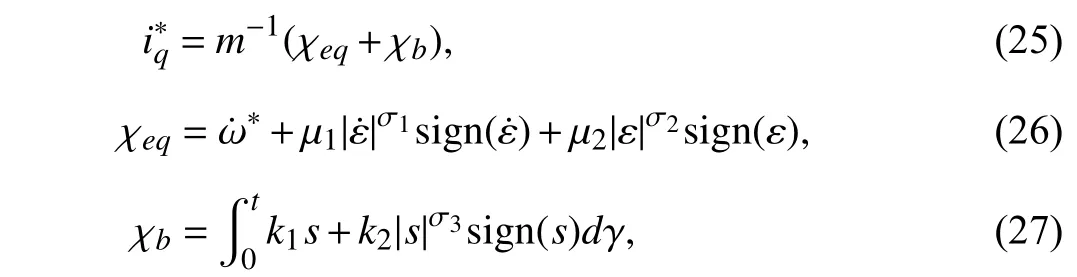
whereεis speed error,sis sliding variable,mis parameter of PMSM and μ1,μ2,k1andk2are the positive constants to be designed.It should be noted that the main idea of TSMC evolved out of seminal work on terminal attractors,and is evoked by the concept of terminal attractors which guarantee finite time convergence of the states.Thus,compared with traditional SMC,TSMC can guarantee that can make the closed loop system converge to equilibrium in finite time.

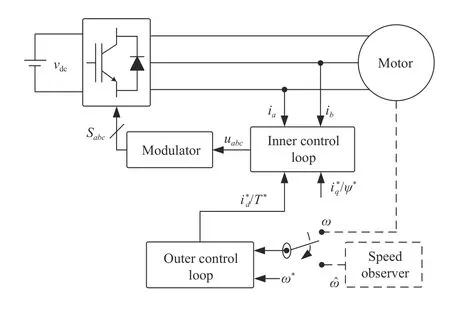
Fig.2.The block diagram of SMC for the motor speed-regulation system.

Fig.3.The control structure for the motor speed-regulation system using terminal sliding mode control.

The simulation and experimental results demonstrated that CFTSMC has superior performance than the conventional approaches.The SMC for motor drive systems is summarized in Tables VI and VII.Here it should be pointed out that the current based SMC method in the inner control loop for motor drives systems is similar to the grid-connected power converters,which can be seen in Table V.Thus there are only the torque and flux variables based SMC methods given in the Table VII.

On the other hand,a number of sensors are used in the systems (e.g.,speed/position sensors),which increases not only installation difficulty but also cost.Therefore,it is of great interest proposing speed/position sensor-less control strategies in order to reduce cost and improve system reliability [98].Many research endeavors have been focused on sensor-less control design problems during the recent years,Kalman filter (extended Kalman filter) [99],adaptive observer [100],and sliding-mode observer [101],and so on.Although most of them are able to get accurate speed or position information,they either depend largely on the machine parameters or require a large computational burden.

With its inherent advantages,order reduction,good dynamic performance and robustness to parameter variations and disturbances,sliding mode observer has widely applied in the sensor-less motor drives.In [102],a flatness-based SOSMC combined with an angular velocity second order sliding mode observer was designed for the stepper motor.The angular displacement and the direct current are chosen as flat outputs such that other states or input variables can be presented as a function of the flat outputs and their time derivatives up to some finite number.The practical stability of the closed-loop system was obtained inherently.For the real-time implementation of the designed control law,the online parameter identification should be taken into consideration.Shtesselet al.[103] designed a parameter observer to estimate the load resistance and parasitic phase resistance.An adaptive interconnected observer with online parameter identification(the stator inductance and the stator resistance) was proposed in [104].It should be noted that above works require the utilization of the current sensors.Wanget al.[105] proposed an adaptive filter with the sliding mode observer for position sensor-less motor drives,and the approach was verified with the experimental results.Two novel sliding mode model reference adaptive system observers were successfully applied in the sensor-less induction motor drive [106].Compared with the classical observer,the dynamics obtained by sliding mode model reference adaptive system observers do not exhibitdamped responses or speed dip.In [107],an adaptive slidingmode observer was designed for sensorless speed control of an induction motor,which contains three observers.Two sliding-mode observers are designed to estimate currents and the third observer is used to estimate rotor flux which is based on the current observers.This can diminish the influence of parameters variations on the flux and speed estimation.The control structure based on adaptive sliding-mode observer for sensor-less speed control is shown in Fig.4,where the block diagram of adaptive sliding-mode observer is presented in Fig.5.Note that the above observers only perform well in high and medium speed since the low signal-to-noise-ratio caused by modeling uncertainty and nonlinearity [108].

TABLE VISMC FOR MOTOR DRIVES: OUTER CONTROL LOOP

TABLE VIISMC FOR MOTOR DRIVES: INNER CONTROL LOOP

VI.FUTURE CHALLENGES AND PROSPECTS OF SMC FOR POWER CONVERTERS

SMC was effective solution for power converters and motor drives during the last decades.However,there are still several remaining issues that should be solved before it can be extensively used in the industry in the near future.

· Despite the advantages of simplicity and robustness,a main drawback of the pure SMC strategies is chattering which is a high-frequency oscillating occurring in the control process.In recent years,new SMC mechanisms such as higher-order sliding mode,terminal SMC and adaptive SMC have been introduced in order to alleviate the chattering problem.Although these new SMC approaches offer promising dynamical properties,theoretical proofs of finite time convergence and stability analysis are still open problems due to the introduction of non-smoothness and discontinuous terms.Future research activities in this area are definitely required.

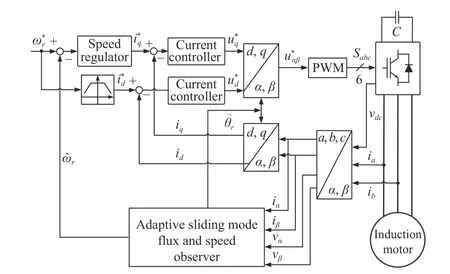
Fig.4.Control structure for sensor-less speed control.

· In commercial applications,the use of SMC for basic loworder power converters has been deemed unrealistic because of higher complexity compared to existing linear controllers.From a cost perspective,the idea of applying SMC in highorder power converters is of great value which provides desired performance over a large operating condition.However,for practical implementation of SMC to power converters,it only allows operating at limited frequency ranges while the ideal operation of SMC requires infinitely high frequency.

Fig.5.The block diagram of adaptive sliding-mode observer.

· Since the control strategies are implemented in digital microprocessor nowadays,the ideal sliding motion,invariability and stability cannot be guaranteed in the continuous time domain due to the discretized sampling.Thus discrete-time sliding mode control is needed,which takes control design in a more generalized sense.Future research about design discretized quasi-sliding mode control schemes for converters and drivers is still needed.

· Considering complex systems whose models have multiple variables,multiple parameters,and nonlinear couplings,it is evident that SMC techniques are inadequate to analyze and predict the behavior of such systems.Intelligent algorithms have proven to be efficient methods dealing with the intricacy and the complexity of the practical industrial systems.Furthermore,due to the fast development of powerful DSPs and field-programmable gate array,high-performance control algorithms can be easily implemented for complex industrial systems.Among various intelligent control techniques,fuzzy logic and neural networks are becoming more and more popular in the applications where the mathematical model is not accurate or the model is ill-defined.Therefore,the integration of intelligent control techniques and SMC can solve the problems met in practical implementations of SMC for complex systems.The major developments in this research area have been outlined in the earlier surveys [5],[7].

VII.CONCLUSIONS

This paper has reviewed the applications of SMC to different types of power converters,i.e.,dc/dc converters and three-phase voltage source PWM converters.Several control schemes used to obtain ac/dc conversion with bidirectional power flow and regulation power factor have also been discussed.SMC is a well-known nonlinear control technique which has achieved high-performance operation in a wide application range.The distinctive feature of SMC is its robustness against parametric uncertainties and external perturbations.The main problem associated with the application of SMC to power converters is its variable switching frequency nature,which causes excessive switching losses and complicated design of output filters.On the other hand,with large penetration of renewable energy in power systems,the power converters have become more and more large-scale and complex.

It is obviously not adequate only using the traditional SMC techniques to control these large-scale converters in the future.Therefore,the integration of intelligent control,multi-agent and data-driven approaches with SMC will become one of the most promising researches in control and power electronics fields.By designing properly,these seminal composite control schemes can enhance the performance of the SMC and simultaneously capture attractive features of the advanced algorithm,which can be extensively applied to control complex power electronics systems and does have a huge potential in industrial applications.