Conflict-Aware Safe Reinforcement Learning:A Meta-Cognitive Learning Framework

Majid Mazouchi,Subramanya Nageshrao,and Hamidreza Modares,

Abstract—In this paper,a data-driven conflict-aware safe reinforcement learning (CAS-RL) algorithm is presented for control of autonomous systems.Existing safe RL results with predefined performance functions and safe sets can only provide safety and performance guarantees for a single environment or circumstance.By contrast,the presented CAS-RL algorithm provides safety and performance guarantees across a variety of circumstances that the system might encounter.This is achieved by utilizing a bilevel learning control architecture: A higher metacognitive layer leverages a data-driven receding-horizon attentional controller (RHAC) to adapt relative attention to different system’s safety and performance requirements,and,a lower-layer RL controller designs control actuation signals for the system.The presented RHAC makes its meta decisions based on the reaction curve of the lower-layer RL controller using a metamodel or knowledge.More specifically,it leverages a prediction meta-model (PMM) which spans the space of all future meta trajectories using a given finite number of past meta trajectories.RHAC will adapt the system’s aspiration towards performance metrics (e.g.,performance weights) as well as safety boundaries to resolve conflicts that arise as mission scenarios develop.This will guarantee safety and feasibility (i.e.,performance boundness) of the lower-layer RL-based control solution.It is shown that the interplay between the RHAC and the lower-layer RL controller is a bilevel optimization problem for which the leader (RHAC)operates at a lower rate than the follower (RL-based controller)and its solution guarantees feasibility and safety of the control solution.The effectiveness of the proposed framework is verified through a simulation example.

I.INTRODUCTION

THE success of next-generation safety-critical autonomous systems has the potential to make a profound impact on a variety of engineering sectors,including aerospace,autonomous cars,and robots.A central component that highly impacts this potential is to formally assure satisfaction of the system’s safety and performance requirements despite uncertainties and changes (e.g.,changes in dynamics,safety boundaries,etc.).

Reinforcement learning (RL) [1] is a powerful methodology for decision making in uncertain environments.RL,as a promising learning-enabled approach,has been widely used in the control system community [2]–[5] for designing optimal feedback policies due to its potential applications in various fields such as robotics [6],scheduling semiconductor testing[7],cyber-physical systems [8],and so forth.A comprehensive survey of using RL for designing optimal feedback policies can be found in [9].Despite its tremendous success,RL works best for systems that perform a single task or operate in a single environment.Lifelong learning has been widely studied in the RL context [10]–[23],to assure that the RL agent continually learns and generalizes its knowledge over time to deal with unforeseen circumstances.These methods can be categorized into three broad classes,namely,multi-task learning [10]–[12],transfer learning [13]–[15],[17]–[20],and meta-RL [21]–[23].Nevertheless,these approaches generalize best to the tasks drawn from the same distribution and do not have a mechanism to guarantee the feasibility of the RL agent in a new circumstance,i.e.,to assure that the assigned objective functions can be safely attained by the RL agent.The main reason for infeasibility is that the relative importance of safety and performance requirements varies as the circumstances changes.For example,while an autonomous vehicle can perform highperformance maneuvers safely in normal circumstances,conflicts between its performance and safety requirements can quickly arise as the circumstance changes (e.g.,change of safety boundaries or system dynamics).A main challenge that arises in safety-critical systems is trading priorities between safety and performance objectives by adjusting the reward function to guarantee achieving as much performance as possible without violating safety constraints.

Designing an appropriate reward function is of utmost importance and challenging for safety-critical systems that must operate in complex environments.To learn the reward function,several approaches have been proposed,including imitation learning (or learning from demonstration) [24],[25],and inverse reinforcement learning [26],[27].In [24],the authors provide a differentiable linear quadratic model predictive control (MPC) [28],[29] framework for the safe imitation learning problem of linear time-invariant systems.An MPC solver and gradient-based learning approach for an imitation learning problem are provided in [25],in which the MPC controller is treated as a generic policy class parameterized by some representations of the cost and dynamics model.While these approaches seem very promising,they require significant prior knowledge (i.e.,expert demonstrations).To solve complex tasks with long episodes and sparse rewards,hierarchical RL algorithms have been proposed in [30],[31].Subskills or options (low-level decisions) discovered in the low-level decision-making layers are reused by the high-level decision-making layer over a longer time scale,effectively shortening the episode length.However,some degree of manual task-specific design is required to select the set of reusable lower-level skills and define high-level policy actions.Moreover,feasibility assurance for safety-critical settings cannot be guaranteed and requires new developments in hierarchical RL settings.

Safe RL [32]–[48] has also recently been widely investigated for control in which the agent tries to learn an optimal policy while also ensuring the satisfaction of safety constraints (e.g.,state and input constraints).These approaches mainly employ control barrier functions,e.g.,[32]–[40],or safety filters,e.g.,[41]–[47],to intervene with a nominal controller and thus guarantee its safety.More specifically,in [35],a safe RL scheme is developed in which an actor-critic-based RL technique is combined with the barrier transformation.The authors in [36] extended the results in [35] to develop an intermittent framework for safe RL algorithms.In [37],a safe RL scheme is developed which is based on optimization of a cost function that is augmented with a control barrier function candidate.In [38],the authors incorporate a barrier function into the reward function and develop a safe RL algorithm that enhances the safety of the electric power grid during load shedding by preventing the system state from violating safety bounds.Reference [39]developed a safe multi-agent RL framework by integrating decentralized multiple control barrier functions,and then based on it,the authors developed a multi-agent deep deterministic policy gradient with decentralized multiple control barrier functions.Nevertheless,these approaches use fixed performance objectives and safety boundaries that are tailored to a specific environment,situation,or task,and consequently,they cannot be generalized to unforeseen circumstances.However,in emerging safety-critical systems,tasks and situations might be largely uncorrelated,and the number of tasks that the system must operate upon is not known a priori.Moreover,the current formulation of safe RL does not allow us to make an appropriate tradeoff between the safety and performance requirements as circumstances changes.

Designing novel learning-enabled controllers with a high capacity for adaptation to resolve conflicts between the system’s requirements is of vital importance for the success of autonomous systems.In this paper,a novel metacognitive RL algorithm is presented to learn a control policy by optimizing a learned function that formally assures safety with a good enough performance.Contrary to the existing meta-RL algorithms,in this paper,we present safe RL algorithm to adapt the focus of attention of RL algorithm for its of performance and safety objectives to resolve conflicts.This will,in turn,assure the feasibility of the reward function in a new circumstance.To this aim,a data-driven receding-horizon attentional controller (RHAC) is employed in a higher metacognitive control layer to adapt the RL reward function.A nonquadratic performance function that employs barrier functions to encode system constraints is leveraged.A viable control solution is then defined as a control solution that assures the boundness (feasibility) of this nonquadratic performance function,which in turn provides performance and safety guarantees.As the mission scenarios develop,the feasibility of the performance function might be jeopardized as a result of a poorly balanced performance function.In this case,the reward parameters must be adapted to the situation to assure the existence of a viable control solution.The problem of finding the optimal set of reward parameters as well as its corresponding optimal policy is cast into a bilevel optimal control problem.The higher-layer RHAC or leader decision maker determines what objectives to attain to achieve viability with the best possible performance.The lower-layer controller or the follower decision maker leverages a policy iteration RL algorithm to determine its corresponding optimal policy.The RHAC leverages a prediction meta-model (PMM) which spans the space of all future meta trajectories using a given finite number of past meta trajectories.The metacognitive capabilities of the adaptation of the reward function is key to the success of truly autonomous systems to determine what objectives to pursue (what hyperparameters to select) to safely achieve their objectives without failing and infeasibility.Exiting safe RL-based control methods [32],[34]–[36] that are not equipped with these metacognitive capabilities will fail to guarantee the feasibility and/or safety of the RL algorithm in ever-changing situations and only work well in structured environments.Therefore,this metacognitive capability will allow RL agents to operate under more complex environments.

II.PROPOSED CONFLICT-AWARE SAFE REINFORCEMENT LEARNING ALGORITHM STRUCTURE OVERVIEW

In this paper,to resolve conflicts between performance and safety requirements as circumstances change,data-driven conflict-aware safe RL (CAS-RL) is proposed to decide on the relative importance or focus of attention on constraints,setpoint values,and performances weights.To this aim,first,the constrained optimal setpoint tracking problem is formulated and a parameterized nonquadratic safety-aware performance function is introduced that employs parametrize barrier functions to encode system constraints.Second,a policy iteration RL algorithm is leveraged to determine the safe optimal policy corresponding to the specified reward function.A viable control solution is then defined as a control solution that assures the boundness of this nonquadratic performance function,which in turns provides performance and safety guarantees.Third,the problem of finding the optimal set of reward parameters to assure that all constraints are consistent and satisfiable at the same time as well as finding the safe control policy corresponding to the specified reward function is cast into a bilevel optimal control problem.To do so,a higher layer RHAC is employed in a higher metacognitive control layer to adapt the RL reward function.This higher layer controller acts as a leader decision-maker and determines the necessary objectives to achieve viability with the best possible performance.Fourth,the RHAC,in the higher layer,leverages a prediction meta-model (PMM) which spans the space of all future meta trajectories using a given finite number of past meta trajectories.Fifth,an algorithm is given to collect several meta-trajectories online and compose them to relearn the meta-trajectory based PMM.

The proposed conflict-aware safe reinforcement learning control framework is shown in Fig.1.An inner low-level RL controller operates in continuous-time and is used to safely stabilize the closed-loop system in an optimal fashion while dealing with unknown dynamics.An outer high-level RHAC determines the optimal attentional parameters that guarantee the feasibility and viability of the lower-level RL controller while achieving the highest performance possible.The details of the inner- and outer-loop designs are given in Section IV.

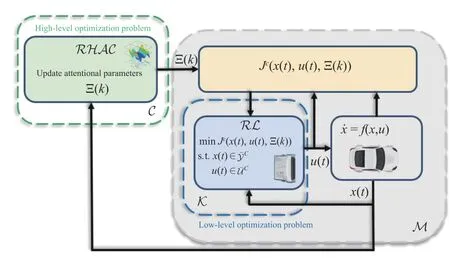
Fig.1.Proposed conflict-aware safe reinforcement learning control framework.C: higher layer controller; M : inner closed-loop system.

III.PROBLEM STATEMENT

In this section,the constrained optimal setpoint tracking problem is formulated and a parameterized safety-aware performance function is introduced in which the attentions of the system to different safety and performance metrics are parametrized.

Consider the non-linear continuous-time system

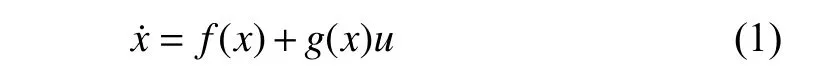
wherex∈ℜnandu∈ℜmdenote the system state vector and the control input,respectively.We assume thatf(x)+g(x)uis locally Lipschitz continuous on a set Ω ⊆ℜnthat contains the origin and that the system is stabilizable on Ω.

The system’s states and control inputs are typically constrained due to some physical and environmental limitations.We consider constraints in the form of bounds on systems’state andcontrol.Let(xi(t),) ≥0describesthep-thconstraint onthe statexi(t)with thebound.Thatis,

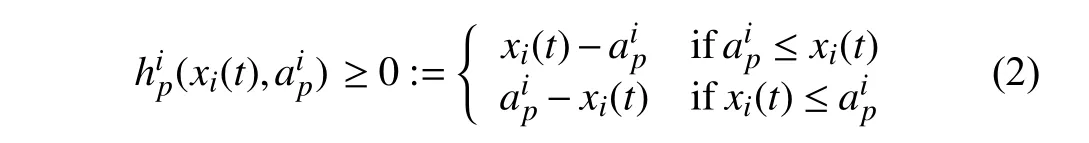
where we define the constraint set

To guarantee achieving a desired behavior with satisfactory performance under constraints,one can optimize an objective function that incorporates a variety of the systems’ sub-goals(e.g.,energy saving,good transient performance,etc.) and their minimization,subject to constraints,which provides an optimal control solution.For setpoint tracking under constraints,the following optimal control formulation can be used.

Problem 1 (Constrained Optimal Setpoint Tracking):Given the system (1),design the control signaluby solving the following constrained optimal control problem:

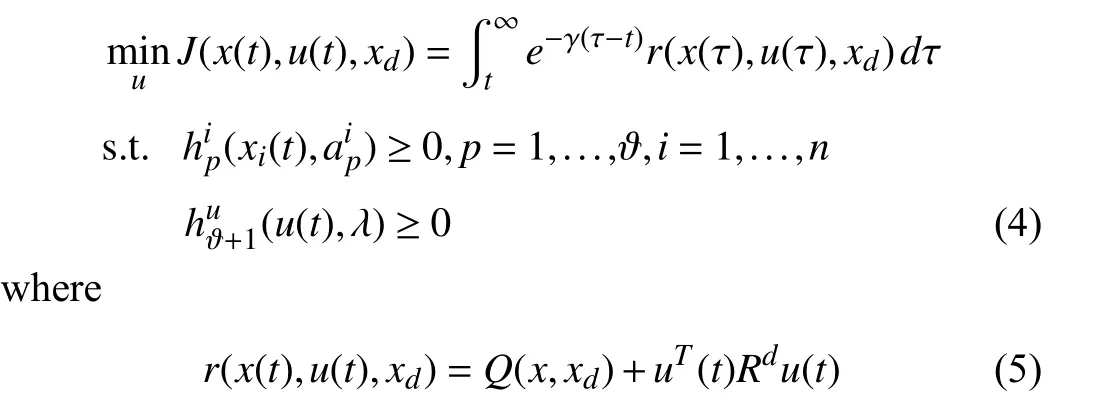
is the reward function,withQ(x,xd):=(x(t)-xd)T Qd(x(t)-xd),whereQd≻0andRd≻0are per for mance weights,andxdis the desired setpoint.

To convert the constrained optimal control Problem 1 into an unconstrained optimal control problem,the barrier method can be used.In the barrier method,assuming that initial states lie inInt(YC),a significant cost is inflicted on points that lie close to ∂YC,thereby forming a “barrier” that does not allow the state to leave the safe region.Therefore,the constraints(xi(t),)≥0,p=1,...,ϑ,i=1,...,n,and(u(t),λ)≥0,will be encoded into the performance function using barrier functions.

Definition 1:Let η(t)∈ℜ and ηd∈ℜ be a scalar variable and its setpoint,respectively.A functionB(h(η(t),a),ηd) is called a barrier function w.r.t the constrainth(η(t),a)≥0 defined in (2),if it satisfies

Problem 2 (Barrier Certified Optimal Control):Given the system (1),design the control signaluby solving the following unconstrained barrier certified optimization problem:

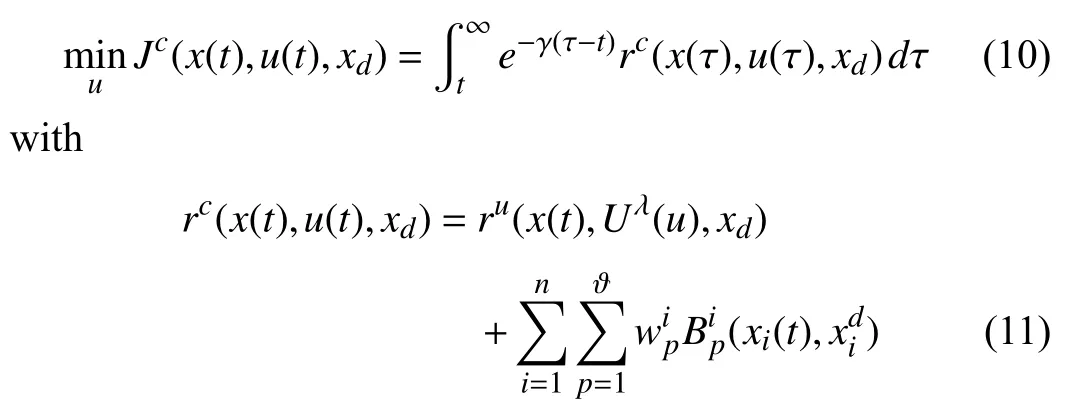
whereis the weight of the barrier function corresponding to thep-th const raint on the statexi(t),andru(x(t),Uλ(u),xd):=Q(x,xd)+Uλ(u)with the nonquadratic integrand [49]

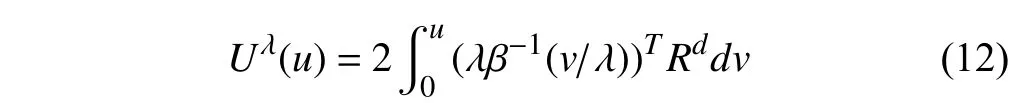
wherev∈ℜmand β(·)=[β1(·),...,βm(·)]Tis a bounded monotonic function (e.g.,t anh(·)).

Note that the nonquadratic cost (11) assures that the optimal control found by minimizing Problem 2 guarantees |ui(t)|≤λ,i=1,...,m[49].

The optimization framework in Problem 2 works well for systems operating in structured environments for which the system is supposed to perform encoded tasks,the constraints boundaries do not change over time,and there is no conflict between the state constraints,control policy constraint,and the desired setpoint.However,for complex systems such as self-driving cars for which the system might encounter numerous circumstances,a fixed reward function cannot capture the semantics of complex tasks across all circumstances.In case of a conflict between safety constraints and/or between performance requirements,i.e.,for the case where there is nou(t) that makesJcbounded,either the constraints will be violated or the performance-oriented part of the rewardrc(x(t),u(t),xd) will become non-zero due to a high-per for man cedem and that can notbe reached,resultinginJc→∞in bothcases.In the for mercase,the systemisno longer safe,and,in the latter case,every control policy is as good as any other,and thus the system can drift around without any guarantee to achieve its main goals.

Remark 1:One might argue that the original performance or reward function in Problem 2 can be appropriately designed in a context-dependent fashion to avoid infeasibility across a variety of circumstances.However,during the design stage,it is generally not possible to foresee circumstances that will cause infeasibility and come up with a context-dependent reward function.This is generally due to time-varying constraints boundaries,modeling errors,unknown disturbances,and operator intervention.

The next section presents a conflict-aware safe RL (CASRL) that adds a meta-cognitive layer on top of the lower-layer RL-based control design to decide on the relative importance or focus of attention on constraints,setpoint values,and performances weights.The presented CAS-RL uses a parametrized version of the performance function (10) to resolves possible conflicts,which is presented next.To parametrize barrier functions,which is required to resolve conflicts between different constraints,slack variables are introduced to the barrier functions for soft constraints in the modified reward function (11): This modifies the boundaries of soft constraints by introducing free variables to be tuned to assure that all constraints are consistent and satisfiable at the same time.Let the soft state constraint set and slack variables set be defined as

whereECis the constraint set of the slack variables.

Now,let us reformulate the performance function (10) in a parameterized form as follow:

Definition 2:Problem 2 with the performance functionJc(x(t),u(t),Ξ) with attentional parameters Ξ is called feasible if there exists a control policyu(t) that makes the performance bounded,i.e.,0 ≤Jc(xu(t),u(t),Ξ)＜+∞ wherexu(t) is the state trajectoryx(t) of the system (1) generated byu(t).

In the sequel,with a slight abuse of notation,Jc(x(t),u(t),Ξ)is used instead ofJc(xu(t),u(t),Ξ).

Theorem 1:Consider the parameterized performance function(17)with attentional parameters Ξ and let the performance functionJc(x(t),u(t),Ξ)be feasible.Then,there exists a unique optimal control policyu*(t)=argminJc(x(t),u(t),Ξ)given by

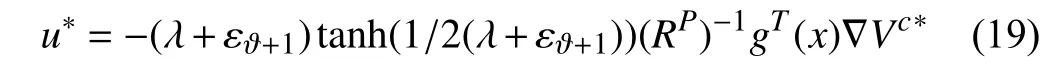
whereVc*is the solution to the following Hamilton-Jacobi Bellman (HJB) equation:

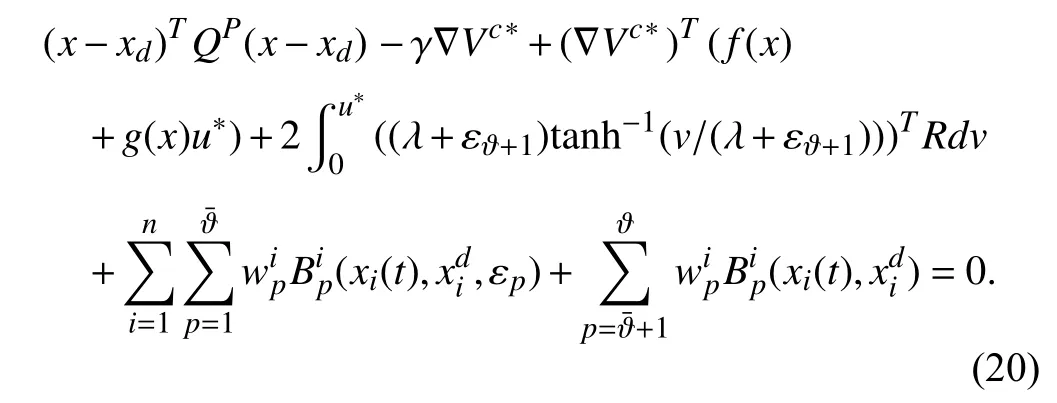
Moreover,the optimal control policy assures that:

1) The setpoint tracking errorer(t):=x(t)-xdis asymptotically stable provided that the discount factor is sufficiently small;

2) The closed-loop system remains safe,i.e.,x(t)∈andu*(t)∈C.

Proof:See Appendix A.

Definition 3:The control policyu(t) is called viable if it guarantees the feasibility of Problem 2,and thus based on Theorem 1 provides both safety and performance guarantees.

IV.META-COGNITIVE BILEVEL LEARNING FRAMEWORK

To guarantee feasibility and learn the optimal control solution at the same time,a bilevel optimal control problem in the following form is proposed in this section.

Problem 3 (Bilevel Optimization Problem):Let the high level control leroperateatanupdat ingrateTS.Find the subopt imal control policyu*(t)from the follow ingonline optimization problem:

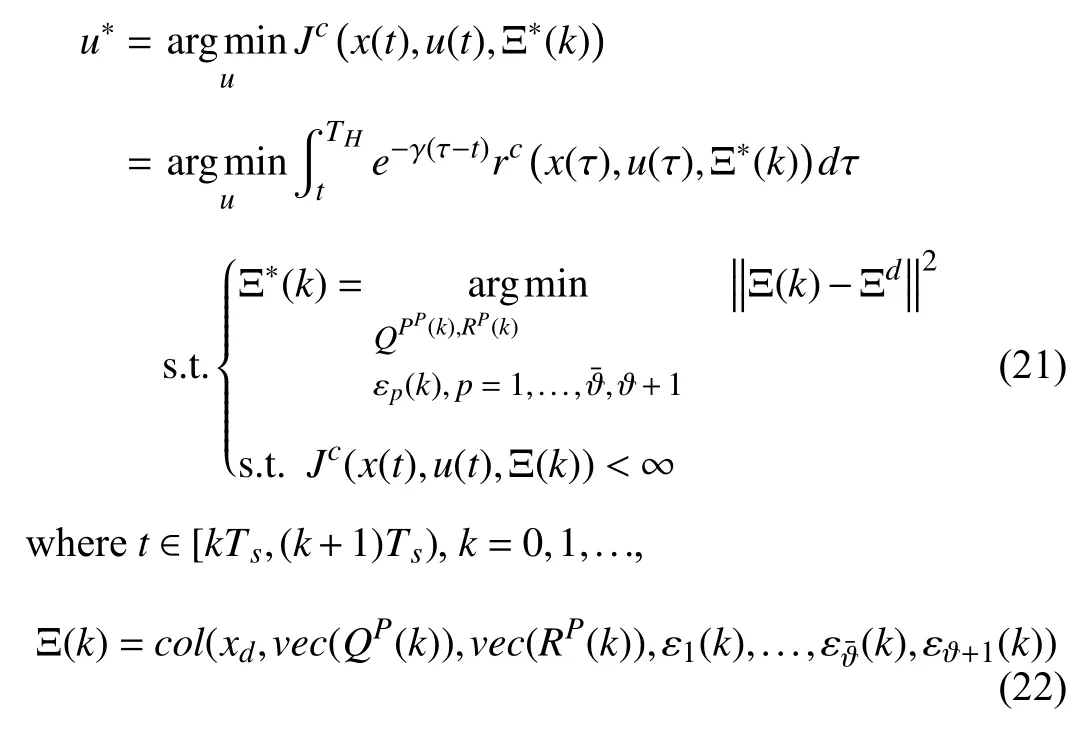
Ξd=col(xd,vec(Q),vec(R),0ϑ¯+1)∈ℜnΞis the desired aspirations for the attentional parameters,andTHis a finite time horizon.

Remark 2:Note that the performance functionJc(x(t),u(t),Ξ*(k))in (21) is finite horizon in practice,which makes it hard to leverage data-driven RL algorithms for solving it.However,sinceTHis assumed large,an infinite horizon RL will be used to approximate the solution to it.Note also thatTSdetermines the frequency of performing an optimization at the higher layer and it does not need to be constant as the higher-layer optimization is changingΞ(k)only if an event is activated indicating that the infeasibility of Problem 2 is imminent.

To solve Problem 3,we adopt a bilevel learning control scheme,illustrated in Fig.1,consisting of:

1) An inner low-level RL controller K that operates at continuous-time and it is used to safely stabilize the closedloop system in an optimal fashion while dealing with unknown dynamics.

2) An outer high-level RHAC C that learns about the optimal attentional parameters Ξ(k) fort∈[kTs,(k+1)Ts) that guarantees the feasibility of the lower-level inner loop M and viability of the lower-layer controller while achieving the highest performance possible.

A.Low-Level RL-Based Control Architecture

In this subsection,the low-layer controller is introduced as an RL controller that optimizes the specified performance with a given attentional parameter Ξ provided by the higherlayer RHAC.Here,for simplicity of notation,we have usedinstead of Ξ(k) ,ε1(k),...,(k),εϑ+1(k),respectively.

Consider the system (2) with a feedback control policyui.Then,its value function corresponding to the performance function (17) becomes

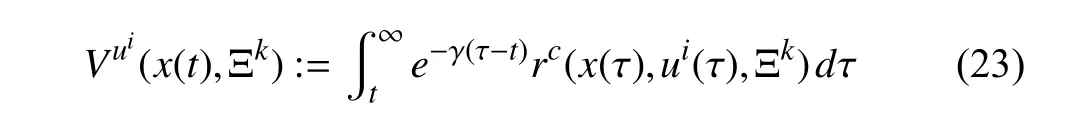
where Ξkis a feasible attentional parameters vector provided by the RHAC and is fixed fort∈[kTs,(k+1)Ts).Taking the time derivative of (23) yields

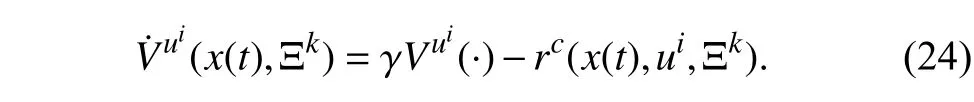
Moreover,using Theorem 1,(24),and the same reasoning as [50],the Bellman equation can be written as follows:

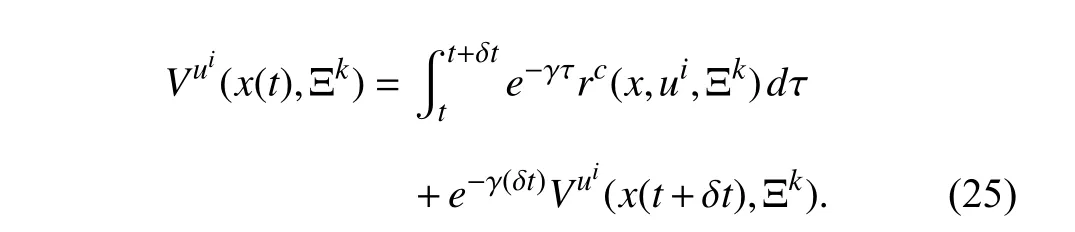
This Bellman equation can be used to evaluate a given control policy and learn its corresponding value function using only measured data samples collected along the system trajectories.Onceapolicyis evaluated using this Bellman equation,i.e.,Vuiisfoundfor a givenui,thenan improved control policy can be found using

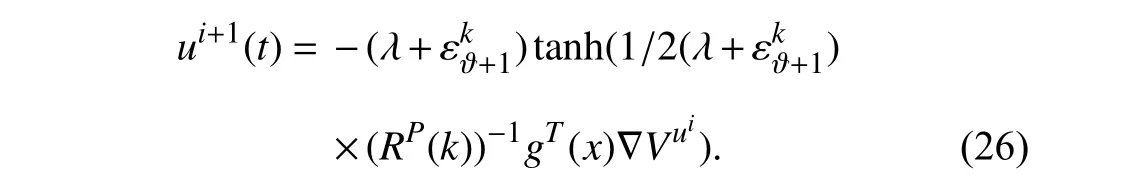
Now,using (25) and (26) the parameterized policy iteration RL algorithm,in which the attentional parameters can be modified by the RHAC to guarantee the feasibility of learning algorithm ∀t∈[kTs,(k+1)Ts) in case of conflict,is given as follows.

Remark 3:Although the higher layer RHAC has a sampling timeTS,it changes Ξkonly when a conflict happens between the constraints and/or the performance which causes the integral term in the right-hand side of (25) goes to infinity,making Problem 2 and thus Algorithm 1 infeasible.

The architecture of the lower-layer RL controller Algorithm 1 is given in Fig.2.

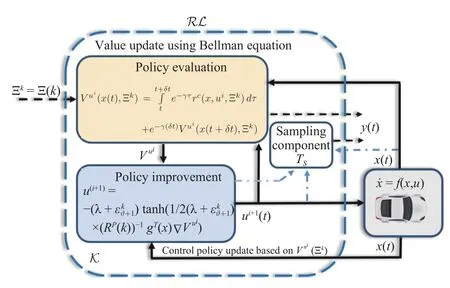
Fig.2.The lower-layer RL control loop.

B.Construction of Predictive Meta-Model

To guarantee the feasibility of the lower-layer RL controller,the higher layer RHAC needs to use a predictive meta-model (PMM) as a dynamical map from attentional parameters Ξ to the state-action-value triple [xT,uT,Vu]T.Consider the inner closed-loop system M with the input Ξ(t)and the internal states [xT(t),uT(t),Vu(t)]T.Assume that the attentional parameters Ξ(t) is evolved such that the feasibility of the RL controller is guaranteed at all time.The following theorem shows that there exists a continuous-time dynamical system that describes the behavior of the inner closed-loop system M with input Ψ(Ξ(t)) where is a nonlinear function of Ξ(t).

Theorem 2:Assume that the attentional parameters Ξ(t) are evolved to guarantee the feasibility of the RL controller at all time.Assume that the barrier functions for soft state constraints are given as

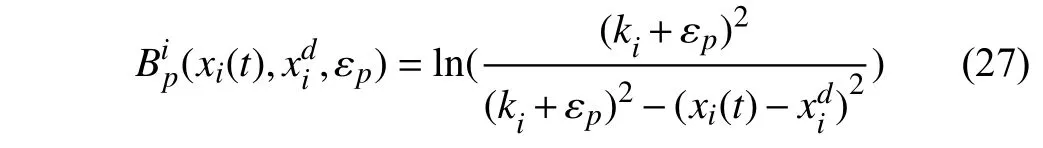
wherep=1,...,andi=1,...,n.Then,

1) There exists a continuous-time dynamical system affine in attentional parameters given by

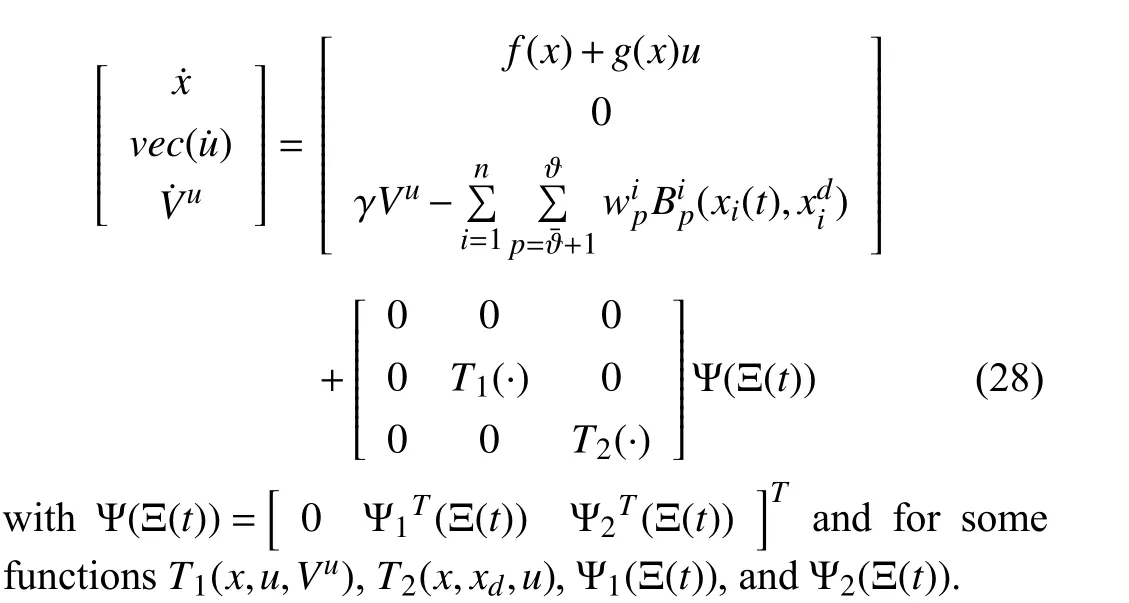
2) The continuous-time dynamical system (28) is safe and stable.

Proof:See Appendix B.

We now define a viability kernel inside which the evolution of the PMM is feasible and assures the feasibility of the RL agent.

Definition 4:The viability kernel of the PMM is defined as

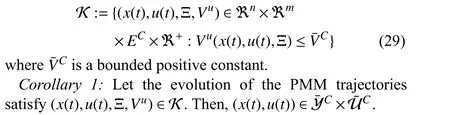
Proof:Theorem 1 showed that when the performance corresponding to a control policy is bounded,then the system remains safe.Based on the definition of the viability kernel in(29),the performance is bounded with a positive function on this kernel which assures the system safety.

To develop a receding horizon controller to adjust the attentional parameters,the system (28) is now discretized using the sampling intervalTSas follows:

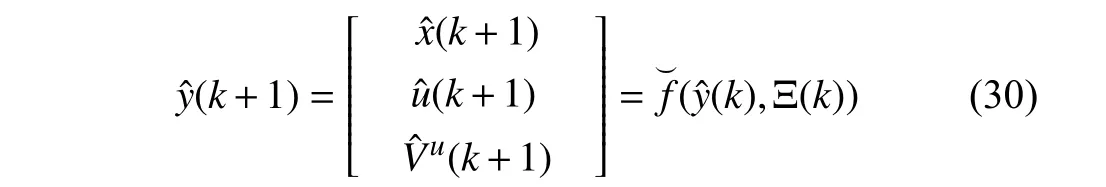
Remark 4:Note that there is no approximation in discretization if Ξ(t) is kept constant during time intervals.Hence,both discrete and continuous-time models (28) and(30) predict the same behavior at the sampling times.

The main objective of the prediction meta-model (PMM)(30) is the prediction of the behavior of the state,control signal,and value function given the attentional parameters{Ξk,k=1,...}.PMM (30) is nonlinear and building it requires knowing the dynamic model of the system (1),which is unknown.Moreover,it is desired that PMM possesses a linear structure for the RHAC in the higher layer.Therefore,since we assume that we do not know the complete and exact model of the system (1),one can construct such a linear structured model by using a data set of inputs (i.e.,Ξ(k)) and outputs(i.e.,[xT(k),uT(k),Vu(k)]T).To this end,a linear structured dynamical system is built as the PMM that can predict the future state,control,and value function of the inner closedloop M based on the measurement of the current and past states,control policies,value functions,and attentional parameters of the system.

The key step in obtaining a linear structured PMM version of a nonlinear dynamical system (30) is a lifting of the statespace to a higher-dimensional space,where its evolution is approximatelylinear.Now,letM(AM,BM,CM,Ξ(k))bethe dynamicalmodelfrom,described in the state-space representation

One can use the following theorem that is inspired by the behavioral system theory [51] to build a data-based equivalent form of PMM (31) of the inner closed-loop system based on the Hankel matrix and recorded meta-trajectories.

Proof:See [52] for the same proof.

Remark 5:Proposition 1 shows that the data-based model in(33),which consists of Hankel matrices that are measured directly from closed-loop experiments performed on the actual closed-loop system M,span the meta-trajectory space of the inner close-loop M and is a data-based equivalent of the PMM (31).Note also that as long as the inner-loop controller has sufficient richness such that the auxiliary input metatrajectoryvP(k) is persistently exciting of orderL+n¯,one can build a data-based equivalent form of PMM (31) of the inner closed-loop system based on the Hankel matrix and the recorded data set DP,using Proposition 1.Furthermore,the sufficient richness of the inner-loop controller can be guaranteed by adding some excitation or probing noise to the inner-loop control input signal.

Note that if the dynamic of the system (1) changes due to a change in the situation (e.g.,system dynamic change),then one can measure another sufficiently large single persistently exciting meta-trajectory to update the PMM model.However,measuring a sufficiently large single persistently exciting meta-trajectory is not a trivial task,and collecting such a long enough persistently exciting meta-trajectory in an online fashion may jeopardize system safety.To obviate this restriction,one solution would be to compose different collected meta-trajectories with short lengths together to construct a single longer meta-trajectory of the lengthL+.The following theorem provides the machinery to compose some different collected meta-trajectories together to construct the trajectory-based PMM (33).

C.Safe Data Collection During Learning

The temporary infeasibility of the RL agent caused by environmental factors (e.g.,situations that result in conflicts in safety constraints temporarily) can be resolved by the PMM without requiring extra data collection for the system dynamics.However,the PMM (33) might become inaccurate after a change in system dynamics,and its wrongful assessment of the inner-loop can violate safety.When safety constraints violation happen due to inaccuracy of the PMM(33),the RHAC cannot find a truly viable controller and it must be updated by collecting extra data from the online interactions.Let the recoverable safe set of the system be given as.Then,the accuracy of the PMM (33) can be monitored.For instance,,i.e.,,but real statex∉implies that the PMM does not work properly and it becomes inaccurate because of the change in system dynamics.In this case,the system starts to collect new data for the reconstruction of the PMM model(33).The data collection has two phases: 1) a safe control(SC) mode for the case where the system states reach the boundary of a predefined recoverable safe set,and 2) a datacollecting phase in between the SC mode for which the system can safely collect data.The SC mode utilizes a backup safe control policy with possibly poor performance.This backup policy can be obtained robustly using minimum knowledge about the system dynamics.For example,a safe backup controller,in the case of an adaptive cruise control problem,can be a myopic rule-based controller or a robust MPC controller that tracks the centerline of the safe setat a safe slow constant velocity.

When the system switches to the SC mode as depicted in Fig.3,the backup safe control policyusafe(x) intervenes and safely controls the system until the time when the system reaches the centerline of the safe set.Then,the proposed bilevel control scheme will continue to work,and the data collection phase will leverage collecting meta trajectories to reconstruct the PMM model.As explained in Theorem 3,since collecting a single large trajectory might jeopardize safety,to safely collect meta trajectories,one can collect multiple different short-length meta-trajectories in between the times that the system is not in SC mode and compose them together to construct a sufficiently large single metatrajectory.To collect short-length meta-trajectories,meta parametersare applied to the closed-loop systemM and collect the corresponding data setwhereLl¯is determined based on the time that infeasibility happens.

D.Meta-Learning Conflict-Aware RL Algorithms

In this paper,we present an iterative RHAC algorithm to solve Problem 3.Our algorithms rely on trajectory-based PMM (33).Algorithm 2 below shows how the results of Sections IV-A–IV-C can be combined to provide the proposed bilevel learning conflict-aware RL based on the metatrajectory-based representation (33),respectively.

Algorithm 2 summarizes the conflict-aware RL algorithm based on trajectory-based PMM (33).

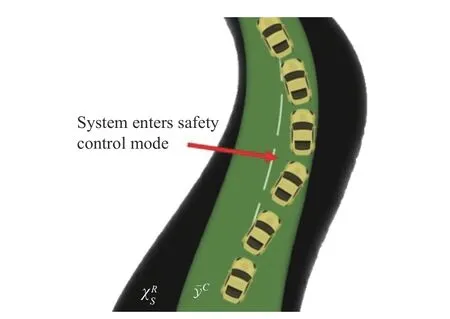
Fig.3.Concept of safety control mode.

Remark 6:Note that if,andECare quadratic,then (42)is a quadratic programming problem,which can be solved efficiently online.

Proposition 2:Let Assumptions 1 and 2 hold and Ξdatabe persistently exciting of orderL+.If the RHAC Problem 4 is feasible atk=0,then the following statements hold.

1) The RHAC Problem 4 remains feasible ∀k∈N;

2)The safety of the overall closed-loop system is guaranteed,i.e.,x(k)∈,u(k)∈,and εp(k) ∈EC,p=1,...,ϑ¯,∀k∈N.

Proof:See Appendix C.

Remark 7:It is worth noting that the proposed approach considers only the reward parameters as hyperparameters to be adjusted to resolve conflicts between safety and performance.This is in sharp contrast to the line of research in deep RL that adjusts hyperparameters including the size of the batch of data and the learning rate,etc.,to improve performance,rather than to assure feasibility.It is also worth mentioning that choosing the updating rateTSdepends on the problem at hand,i.e.,plant dynamics,the rate of changes in the environment,and so forth.On one hand,a faster rate generally improves the bandwidth of the high-level learning system,but can adversely affect the computational burden.On the other hand,a slower rate reduces the computational burden,but deteriorates the capability of the system in responding fast to changes in the environment.Depending on the problem at hand,one should choose a rate that enables the high-level learning system to respond fast enough to changes in the environment with an acceptable computational efficiency.

V.SIMULATION RESULTS

We provide a case study to show the validity of the proposed control scheme,where the control problem of steering control of an autonomous vehicle in obstacle avoidance maneuvers depicted in Fig.4 is considered in this section.The objective in this scenario is to avoid obstacles when any obstacle appears and then bring the vehicle back to its original path on a road when the obstacle is passed.

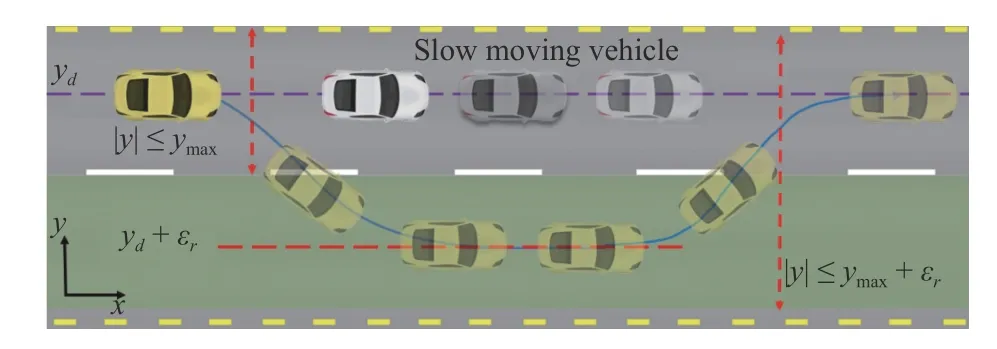
Fig.4.The scenario of lane changing in order to continue the journey for a fast-ego vehicle by passing a slow-moving vehicle.

Consider the following dynamics for a single-track bicycle model vehicle:

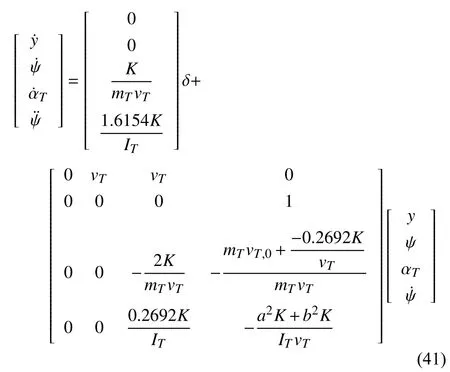
wherey(t) and δ(t) denote the vertical position and steering angle of the controlled vehicle along its lane,respectively.Moreover,ψ and ψ˙ are the yaw and yaw rate,respectively,αTis the vehicle side slip angle,and=vTand=0,wherexandvTare the longitudinal position of the controlled vehicle and vehicle velocity,respectively.Other vehicle parameters are listed in Table I.

The basic objective of the ego vehicle is to follow its path,i.e.,achieve the desired positionyd,and keep the vehicle in the safe road envelope.i.e.,to assure |y(t)|≤ymax.Moreover,it is also required that the distance between the ego vehicle with the coordinatesy(t) and its immediately preceding vehicle with the coordinatesyp(t) be in a safe range.That is,

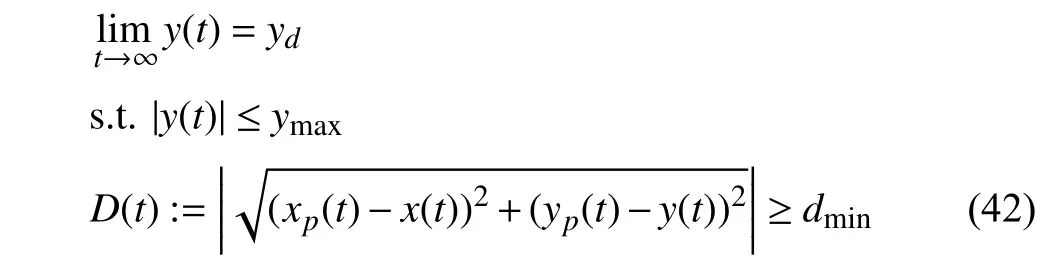
wheredminis the minimum required distance between themass center of two vehicles.

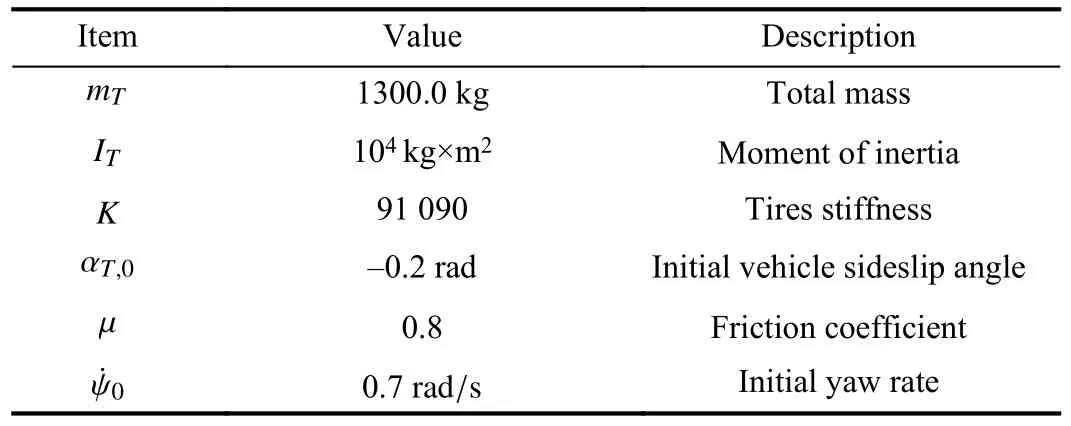
TABLE IEGO-VEHICLE PARAMETERS

Hard Constraints:The control and safe distance constraints in terms of barrier functions are written as

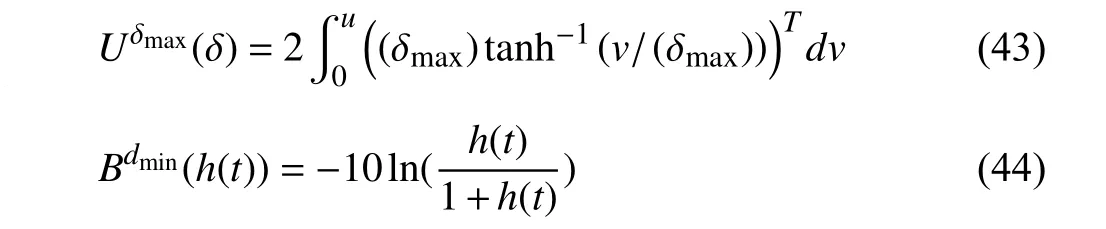
whereh(t):=D(t)-dmin≥0.

Soft Constraint:The goal is to keep the vehicle in the safe road envelope,however,here we assume that there exists a recoverable safe road envelope |y(t)|≤ymax+εmaxwhereεmaxis the maximum recoverable slack variable.This constraint can be written as follows:

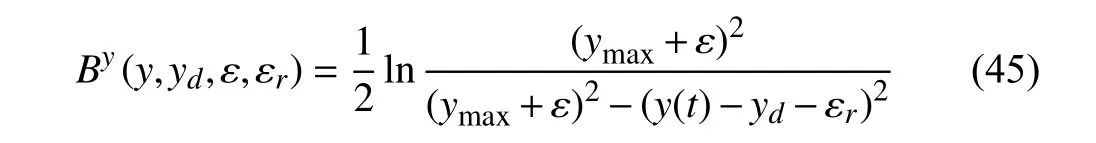
where | ε|≤εmaxand | εr|≤ymax+εmax.

The performance objective of the inner-loop RL controller is chosen as

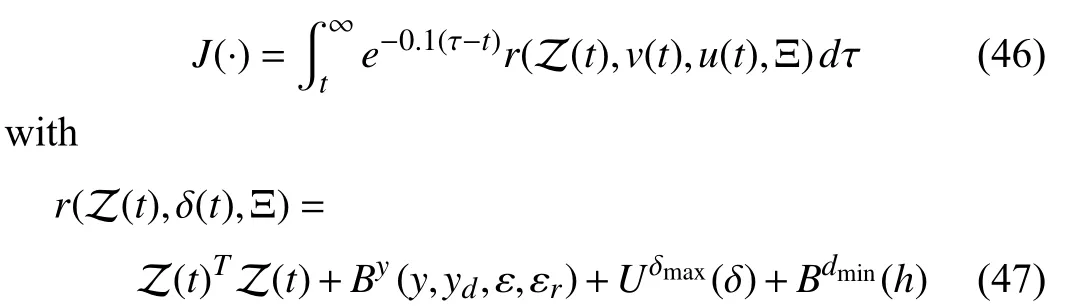
where Z (t):=[y(t)-yd-εr,ψ,αT,]Tand Ξ =col(ε,εr).

The following values are used: δmax=±50 deg,yd=0,the ego vehicle and slow-moving vehicle velocities are 8 m/s and 6 m/s,respectively,anddmin=3.3 m.In performing closedloop experiments,the ego vehicle and the preceding vehicle are initialized aty(0)=0 m andyp(0)=25 m.

First,it is shown that existing safe RL algorithms without metacognitive capability (i.e.,the proposed high-level attentional layer) cannot work properly and guarantee feasibility of RL algorithm and thus will not satisfy safety under the conflict in the scenario in the simulation.To this aim,the method developed in [35] is first applied to the ego vehicle.Note that the safe RL algorithm developed in[35]–[37] employs barrier functions to ensure the satisfaction of safety constraints.One can see from Fig.5 that conflict may arise between (50) and (51) as depicted in Fig.5.Therefore,based on Fig.5,the RL Algorithm 1 cannot operate properly anymore since the value function (52) became very large in a short period of time (t∈[9.574-10.42]) which drives the ego-vehicle to reach and cross the boundary of|y(t)|≤2and cause the termination of the RL algorithm at pointt=10.42 s.Note that the natural logarithm functionln(x)is defined only forx＞0 and it is undefined for negative numbers.

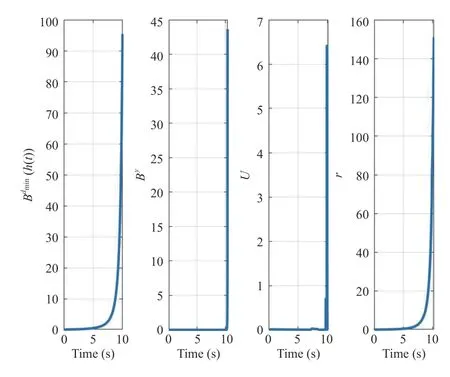
Fig.5.Evolution of the barrier functions and reward applying the method developed in [35].

To learn about using the proposed conflict-aware RL,we first collect the data-set DPwithN=90 by performing one off-line closed-loop experiment in which sufficient richness of the data-set DPis ensured by adding a small probing noise consisting of sinusoids of varying frequencies to the attentional parameters.Then,the proposed online learning scheme is applied to the ego vehicle.To this aim,the attentional parameter Ξ is computed by solving Problem 4 and applied in a receding-horizon fashion,with sampling timeTS=0.115 s and Ξd=col(0,0) using the MATLAB Model Predictive Control Toolbox.All the computations are carried out on an i7 1.9 GHz Intel core processor with 8 GB of RAM running MATLAB R2019b.The prediction horizon is set asL=38.

The continuous-time optimal signal control of the innerloop control and the evolution of the states are shown in Figs.6 and 7.Note that it is desired to drive the ego vehicle states to the origin without violating the hard and soft constraints.Fig.8 shows the successive frames of the ego vehicle and the slow-moving preceding vehicle where the red squares represent the ego vehicle and the cyan squares denote the preceding vehicle.The lower level controller algorithm is implemented as in Algorithm 1.The activation functions and weights chosen asand [W1,W2,W3,W4]T.The reinforcement interval δt and discount factorγ are selected as 0.02 and 0.1, respectively.To satisfy the persistence excitation condition, a small probing noise consisting of sinusoids of varying frequencies,0.1(sin(0.1t))6×cos(1.5 t) + 0.03(sin(2.3t))4cos(0.7t) + 0.14(sin(2.6t))5+0.07(sin(3t))2cos(4t) + 0.1sin(0.3t)(cos(1.2t))2+ 0.04(sin×(1.12t))3+ 0.05cos(2.4t)(sin(8t))2+ 0.03sin(t)(cos(0.8t))2+0.07(sin(4t))3+ 0.114cos(2t)(sin(5t))8+ 0.4(sin(3.5t))5), is injected into the control input to excite the system states.Evolution of the RL critic weights during the learning process with attentional parameter Ξ are depicted in Figs.9 and 10.Based on Fig.10,the proposed Algorithm 1 operates properly by softening the constraint bound of the safe road envelope|y(t)|≤ymaxand slacking the desired set-pointydonly when the infeasibility of RL agent is imminent.As a consequence,no conflict has occurred between the modified set-point and constraint (45) with the hard constraints (43) and (44).

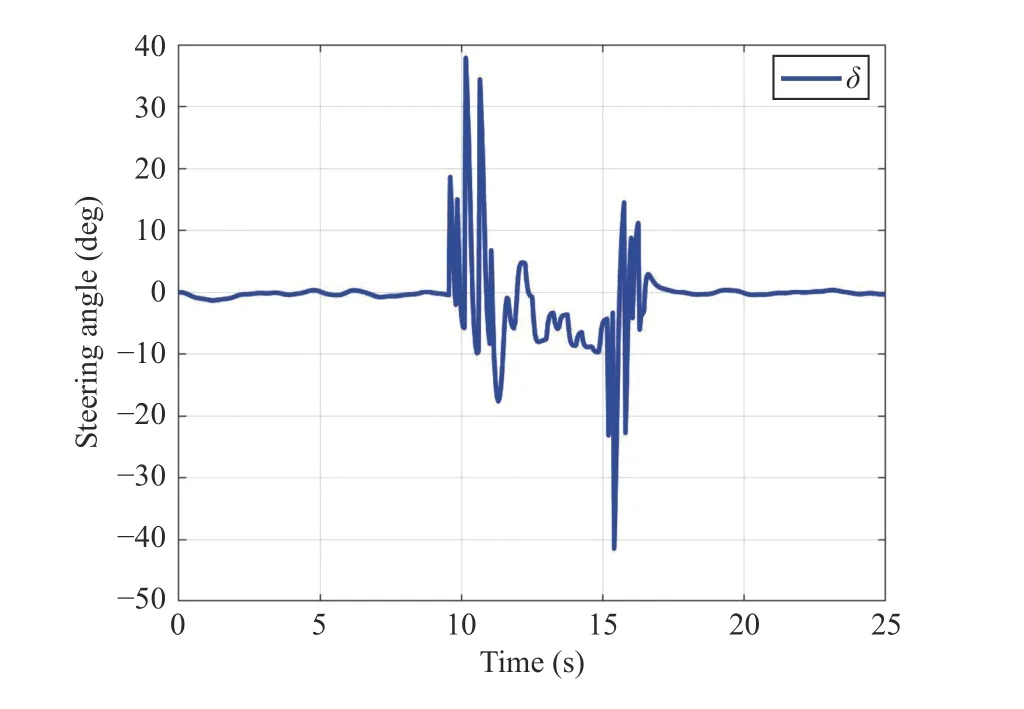
Fig.6.Optimal signal control of the ego vehicle.

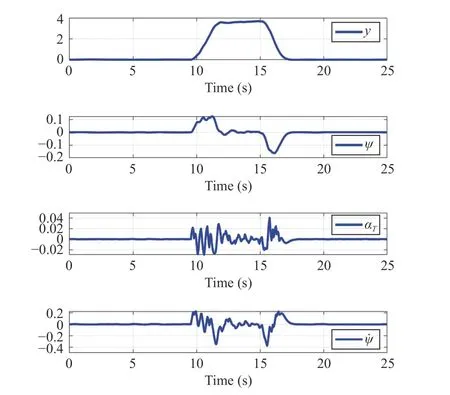
Fig.7.Evolution of the states.

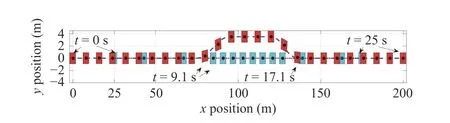
Fig.8.Successive frames of the ego vehicle (red squares) and the slowmoving preceding vehicle (cyan squares).

VI.CONCLUSION

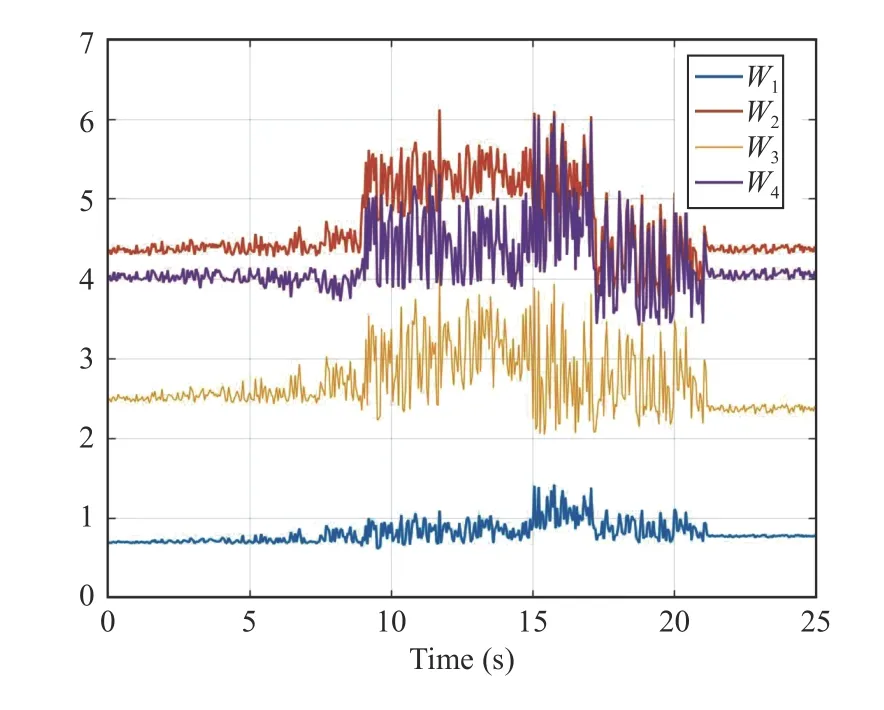
Fig.9.Evolution of the RL weights during learning process.

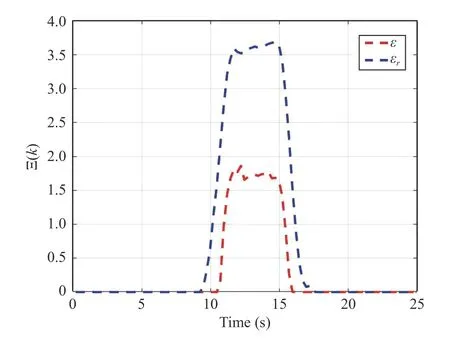
Fig.10.Evolution of the attentional parameter Ξ.

A conflict-aware safe reinforcement learning (RL)algorithm is proposed for the control of complex autonomous systems.Conflicts between the constraints and performance metrics are being resolved by employing a data-driven RHAC in a higher layer control.This high-level RHAC is a datadriven meta-cognitive attentional controller that adapts the systems’ reward function and safe set based on the reaction curve of the RL controller to assure the feasibility of its solution and its alignment with the designer’s intention.For future work,we intend to extend the approach of this paper to handle the computational delays and measurement noise.The effectiveness of the proposed framework is verified on a simulation example.

APPENDIX A

PROOF OF THEOREM 1

The proof has two parts.Based on (17),define the value function

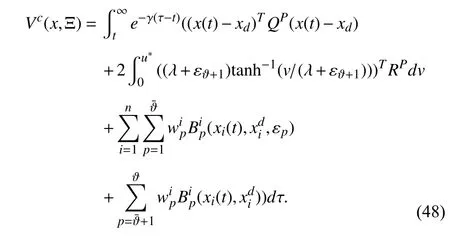
Using Leibniz’s rule [54] to differentiateVc(x,Ξ) along the system trajectories (1),the following tracking Bellman equation is obtained:

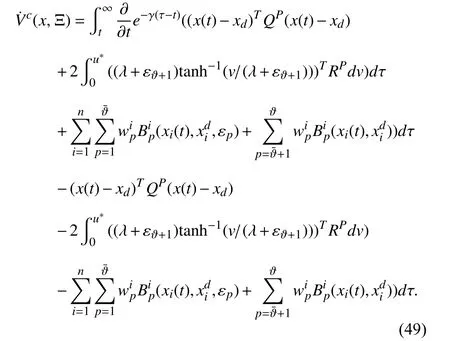
Noting that the first term on the right-hand side of (49) is equal to γVc(·),gives

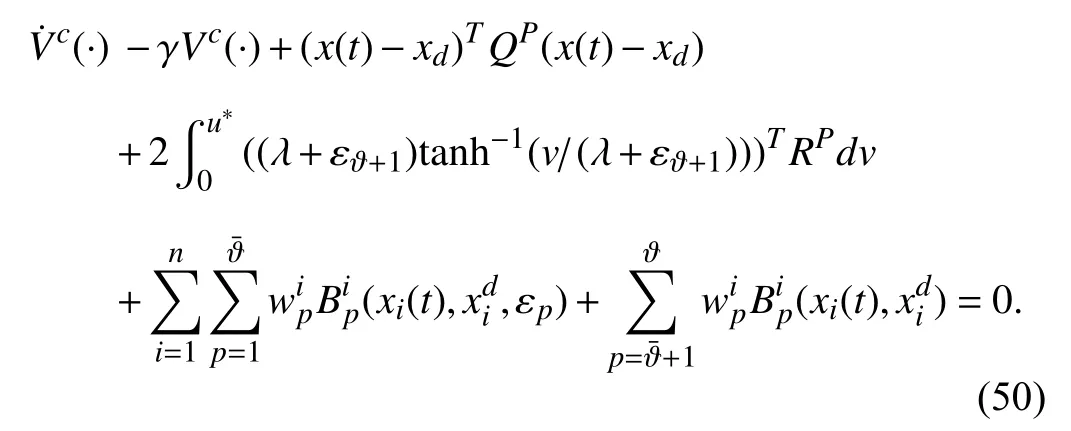
Now,define the Hamiltonian function

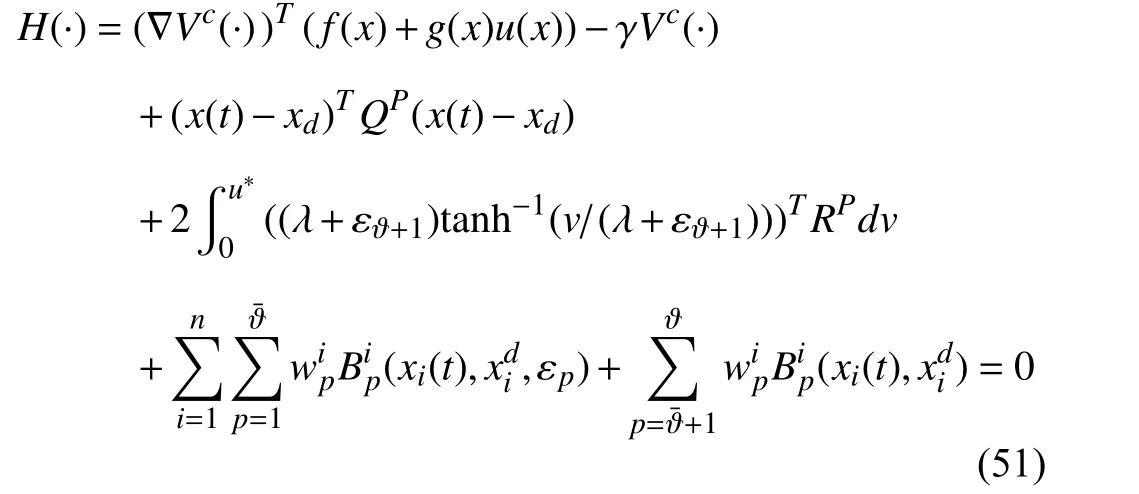
where ∇Vc(·)=∂Vc(·)/∂x.Employing the stationarity condition,i.e.,∂H/∂u,on the Hamiltonian (57),the optimal feedback control policy is given by (17) where ∇Vc*is the solution to the Hamilton-Jacobi (HJ) equation (20).Now,we show thatu*(x) corresponding to the optimal costVc*is the unique solution Problem 2.Let us assume that(x)corresponding to the optimal costcis another optimal solution.Using [52,Theorem 3.19] along with the solutions of the closed-loop system composed of (1) and(x)= -(λ+εϑ+1)tanh(1/2(λ+εϑ+1))(RP)-1gT(x)∇c,one has

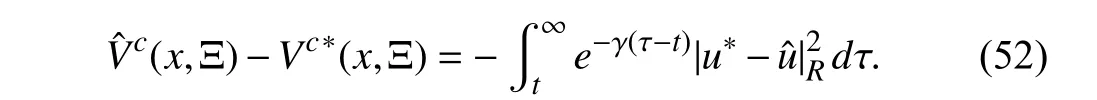
Now,we show thatu*is stabilizing in the sense of Lyapunov.The Lyapunov function candidate is chosen as follows:

which implies that the regulation error is bounded for the optimal solution.The rest of the proof of part one follows from a similar development as in [54,Theorem 4].This completes the proof of part one.

To show that the optimal control is safe and guarantees setpoint regulation,based on the definition of the feasible performance function since there exists a control policy to make the performance bounded,the optimal control policy which minimizes the cost will certainly make the performance function bounded and the boundedness of the optimal value functioncorresponding tou*(x)implies that,...,nandx(t)∈.

APPENDIX B

PROOF OF THEOREM 2

The proof has two parts.Suppose that Algorithm 1 works as a synchronized policy iteration.Using (1),(24),and (25),one has

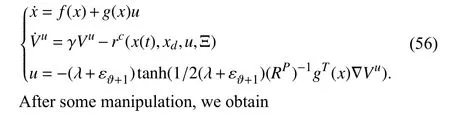
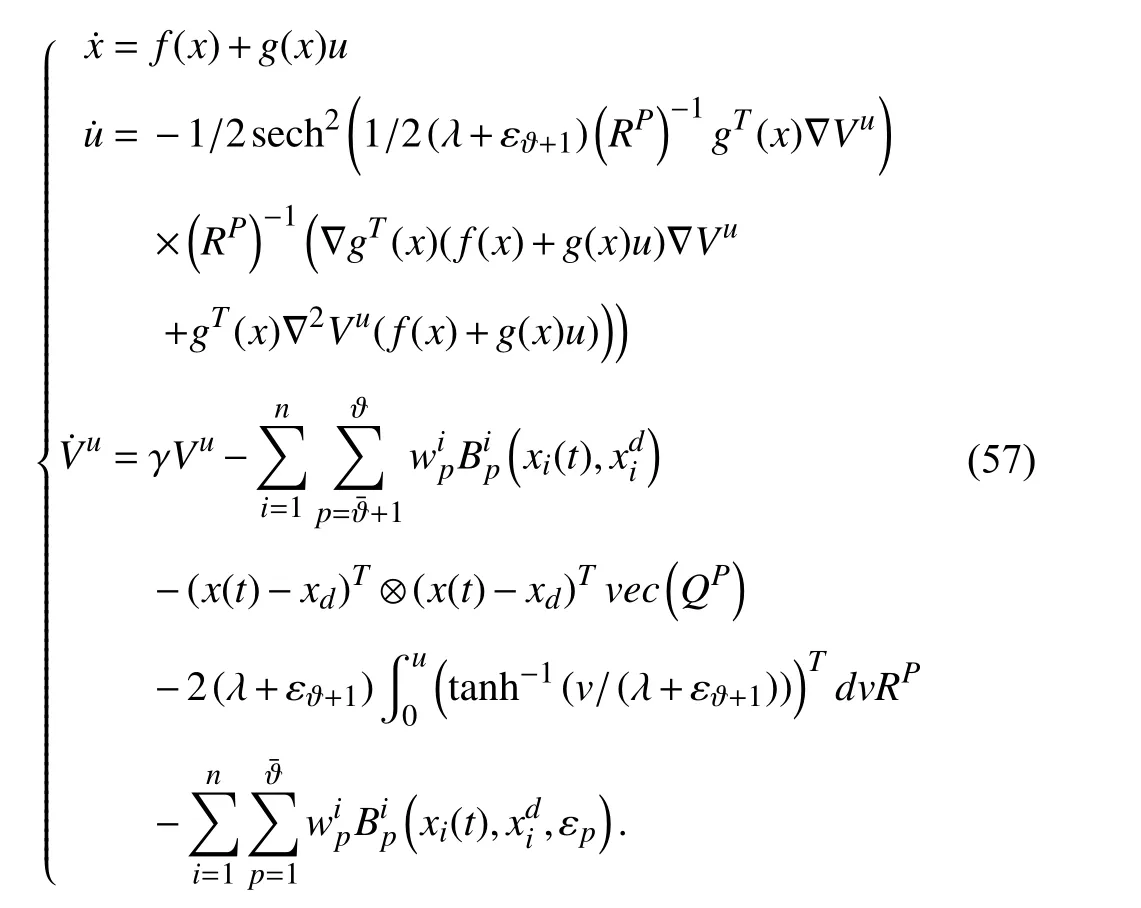
Using (27) and performing some manipulations yields

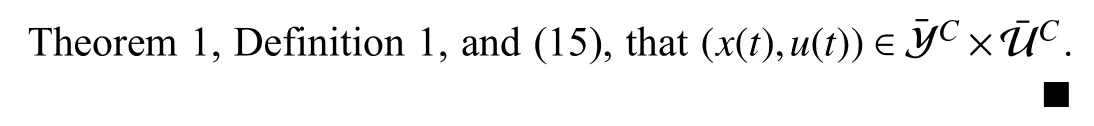
APPENDIX C

PROOF OF PROPOSITION 2