Adaptive Control of Discrete-time Nonlinear Systems Using ITF-ORVFL
2022-01-26XiaofeiZhangHongbinMaWenchaoZuoandManLuo
Xiaofei Zhang,Hongbin Ma,Wenchao Zuo,and Man Luo
Abstract—Random vector functional ink (RVFL) networks belong to a class of single hidden layer neural networks in which some parameters are randomly selected.Their network structure in which contains the direct links between inputs and outputs is unique,and stability analysis and real-time performance are two difficulties of the control systems based on neural networks.In this paper,combining the advantages of RVFL and the ideas of online sequential extreme learning machine (OS-ELM) and initial-training-free online extreme learning machine (ITFOELM),a novel online learning algorithm which is named as initial-training-free online random vector functional link algo rithm (ITF-ORVFL) is investigated for training RVFL.The link vector of RVFL network can be analytically determined based on sequentially arriving data by ITF-ORVFL with a high learning speed,and the stability for nonlinear systems based on this learning algorithm is analyzed.The experiment results indicate that the proposed ITF-ORVFL is effective in coping with nonparametric uncertainty.
I.INTRODUCTION
MOST conventional control approaches can not provide satisfactory control performance for complex systems,such as complex industrial process control systems,robot control systems and so on,due to the difficulties in developing exact mathematical models for nonparametric uncertainties of systems (e.g.,frictional force,unmodeled dynamics).Neural networks (NN) are a good class of nonlinear function approximators [1].With enough history data,and it is possible to estimate nonparametric uncertainty using NN.Radial basis function (RBF) networks belong to a class of single-hidden layer feedforward neural networks (SLFNs) that do not contain the direct links between inputs and outputs,and they have been shown to perform well in solving many practical problems [2]–[5].In recent years,several new RBF architectures have been proposed with the aim of providing better performance.The standard learning algorithm of RBF networks is the conventional gradient descent algorithm.Extreme learning machine (ELM) [6],in which the input weights and hidden layer biases of networks are chosen randomly,and the output weights are determined by the Pseudo-Inverse of hidden layer output matrix,is used to train SLFNs [7].In order to train SLFNs using online data,some online learning algorithms were introduced,such as online sequential extreme learning machine (OS-ELM) [8],regularized online sequential extreme learning machine(ReOS-ELM) [9],initial-training-free online extreme learning machine (ITF-OELM) [10],etc.Although,the learning speed of ELM is extremely fast,the stability of ITF-OELM for nonlinear systems has not been analyzed.
Random vector functional link (RVFL) network is a randomized version of the functional link neural network [11],[12].RVFL contains more information by the direct links between inputs and outputs.RVFL was proposed in [13],and learning and generalization characteristics of RVFL were discussed in [14],[15].In [16],Igelnik and Pao proved that the RVFL network is a universal approximator for a continuous function on a bound finite dimensional set with a closed-form solution.
Usually,RVFL network is trained by offline data.The stochastic gradient descent back-propagation (SGBP)algorithm is used to train RVFL using online data,but it suffers from slow training error convergence as a large number of training data may be required.In this paper,inspired by ITF-OELM and broad learning system (BLS) [17],a novel online learning algorithm which is named as initialtraining-free online random vector functional link algorithm(ITF-ORVFL) is investigated for training RVFL using online data.ITF- ORVFL is different from ITF-OSELM,the update formulae is mended,so that the stability for nonlinear systems based on this learning algorithm can be guaranteed.Compared with the the SGBP algorithm,the link vector of RVFL is determined based on the sequentially arriving data by ITFORVFL,so the learning speed of ITF-ORVF is very fast.In order to verify the effectiveness of ITF-ORVFL,ITF-ORVFL is applied in a robot servo control system based on vision for coping with nonlinear uncertainty.
This paper is organized as follows.RVFL is briefly introduced in Section II.In Section III,we introduce ITFORVFL.In Section IV,the robot servo control system based on vision is explained.In Section V,two experiment examples are given to verify the effectiveness of ITF-ORVFL in coping with nonlinear uncertaiies.Our conclusions are given in Section VI.
II.RANDOM VECTOR FUNCTIONAL LINK
RVFL network is shown in Fig.1,and actual values of the weights from the input layer to enhancement nodes can be randomly generated in a suitable domain and kept fixed in the learning stage.The input features of RVFL are firstly transformed into the enhanced features by enhancement nodes,and input weights and biases of the enhancement nodes are randomly generated.At output layer,all the enhanced and original features are concatenated and fed into output neurons.
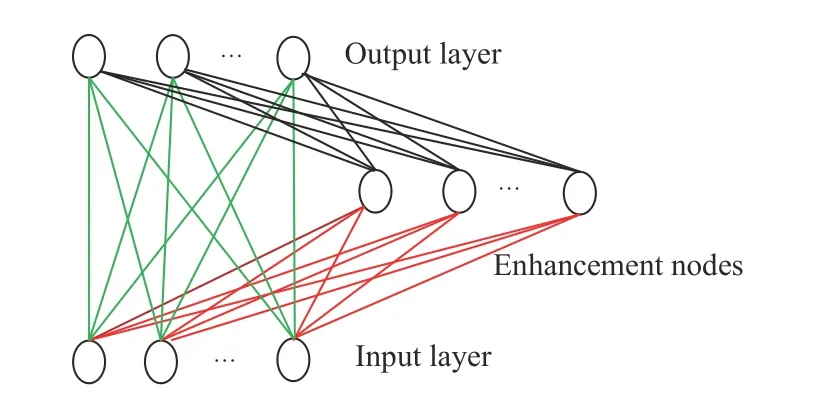
Fig.1.The structure of RVFL.
As the RVFL network has highly beneficial direct links,it is different from the RBF network.
The training procedure of RVFL is similar to ELM and contains two stages: random feature mapping and linear parameter solving.For the output of the RVFL withMinput nodes,Lenhancement nodes and one output node has the following form

andG(·) is the active function (additive or radical basis function) of the enhancement node with parameterswl∈RM,bl∈R,and β is a link vector.
For RVFL,only the link vector β need to the determined by solving the following problem:

whereNis the number of data samples,andhiis a vector version of the concatenation of the original features as well as the enhanced features.Directly solving the problem in (5) may lead to over-fitting.In practice,a regularization on the solution or preference of the solution with smaller norm [18]can be adopted to obtain the solution.A straightforward solution within a single learning step can be achieved by the pseudo-inverse [16],[19],among which the Moore-Penrose pseudo-inverse,is most commonly used,and

whereHandTare matrix versions of the features and targets by stacking the features and targets of all data samples,andH†is the Moore-Penrose generalized inverse ofH.Another alternative is theL2 norm regularized least square (or ridge regression),which solves the following problem:
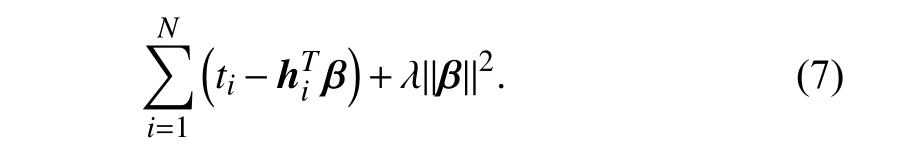
The solution is given by
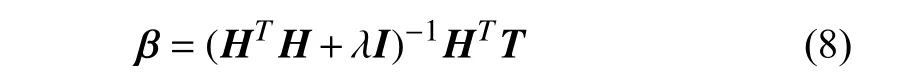
where λ is a regularization parameter.
III.INITIAL-TRAINING-FREE ONLINE RANDOM VECTOR FUNCTIONAL LINK
It should be noted that the afore mentioned theorems assume the availability of complete training data and use (6)or (8) for calculating the link vector β,however in real applications,the training data may arrive chunk-by-chunk or one-by-one (a special case of chunk).Hence,the batch algorithm for RVFL has to be modified for this case so as to make it online sequential.
We must find the learning for mulae for the online sequential learning process.Given a chunk of initial training set,andN0≥(L+M),then the solution of‖H0β-T0‖is

When another chunk of data is given,andN1≥(M+L),the problem then becomes minimizing
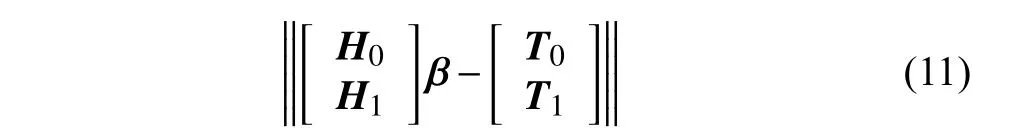
whereH1is explained in (12) (at the bottom of this page),and
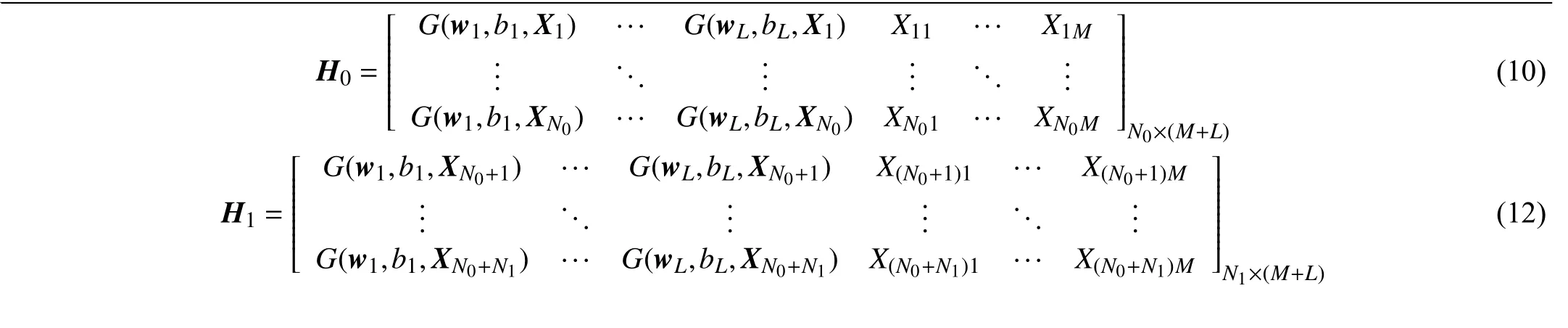
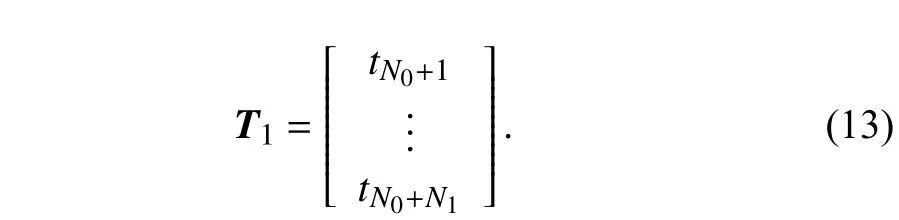
Considering both chunks of training data setsand,the link vector becomes
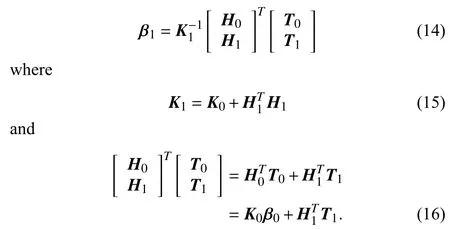
Combining ( 14),(15) and ( 16),β1is given by
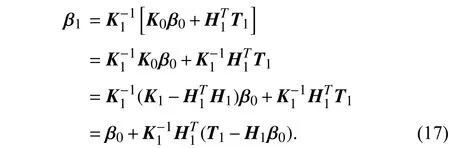
When thekth chunk of data set is received
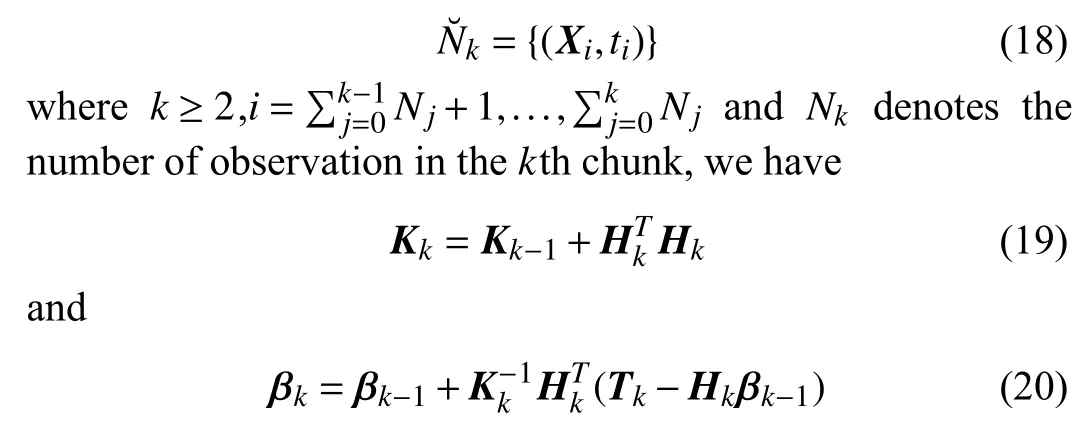
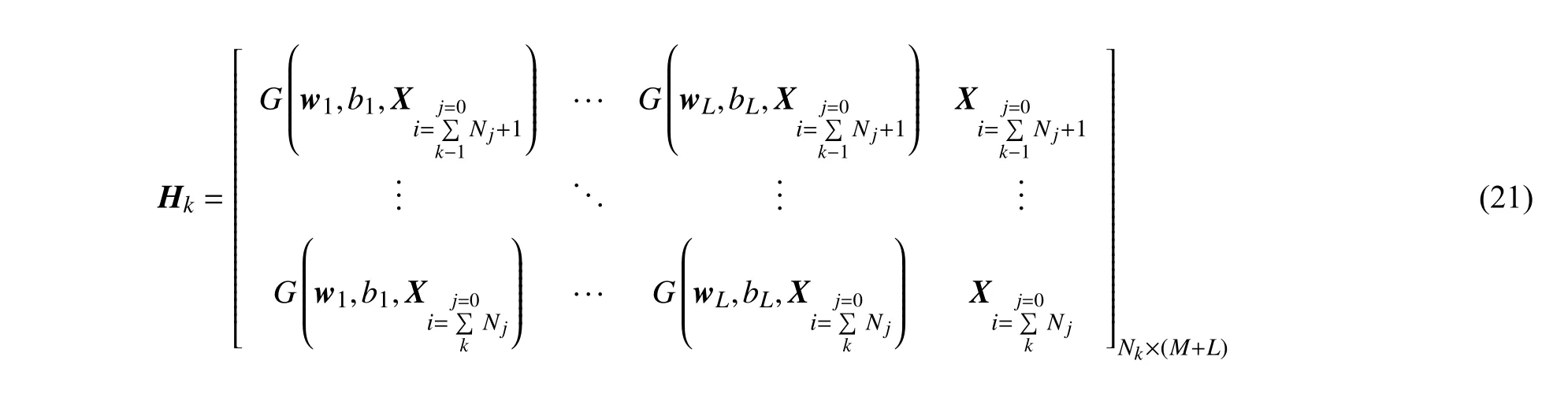
whereHkis explained in (21) (at the bottom of this page.) and
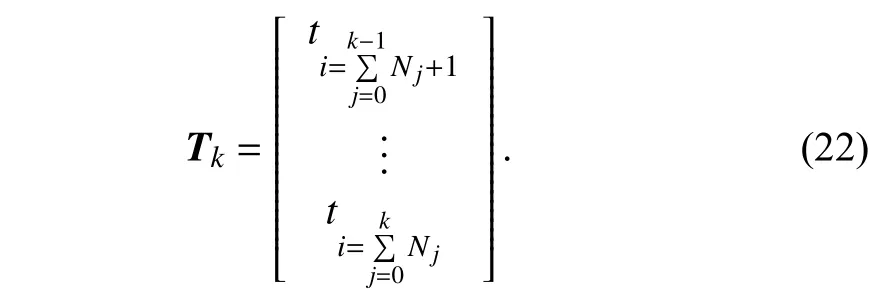
Note that the size ofKkis (M+L)×(M+L),and the value of (M+L) is often quite large.In order to reduce the computational cost for inverse matrix in the case whereNk≪(M+L),from (19),the update formula foris
derived using the Woodbury formula as
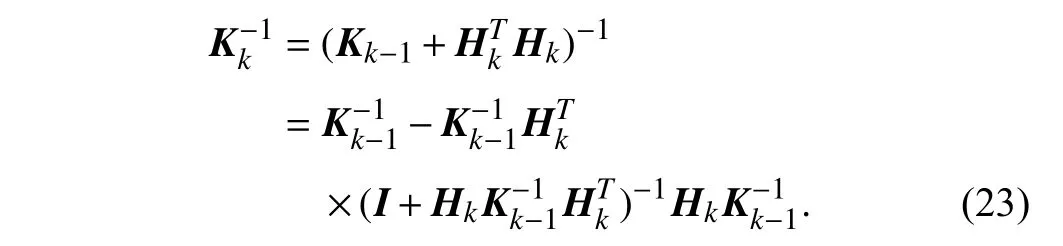
For the convenience of expression (23),we define
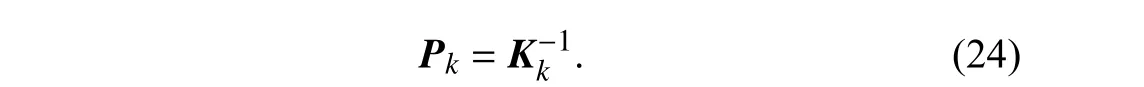
Then,the update formula for βkcan be written as
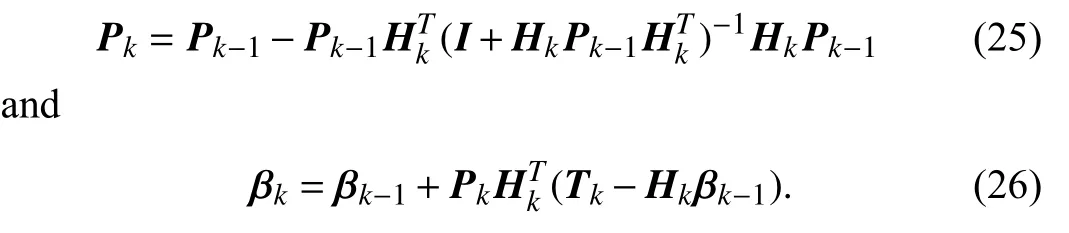
Remark 1:From (25) and (26),it can be seen that the sequential implementation of the least-squares solution (8) is similar to recursive least squares (RLS).Hence,all the convergence results of RLS can be applied here.
OS-ELM is an efficient online version of ELM,and the sequential implementation of OS-ELM is similar to RLS.ITFOELM is an improved version of OS-ELM,and it incorporates the regularization factor λ and forgetting factorρ and thus can yield good generalization performance for noisy data and time-varying models.In this paper,inspired by ITFOELM and BLS,ITF-ORVFL is introduced.
The weight updating formula of ITF-ORVFL for thekth arriving data is

where 0 <ρ <1 and ρ is the forgetting factor of ITF-ORVFL that gives the more recent arriving data a higher contribution to the output weight adjustment.
The initial conditions ofP0and β0could be set as
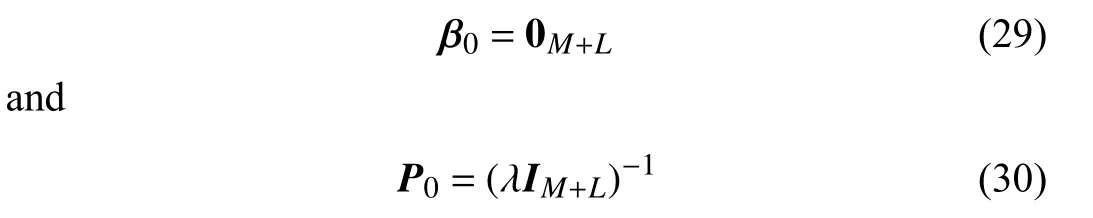
where 0Lis a vector of all zeros with size (M+L)×1.
In fact,this way of initializing β0andP0is a common initialization setting for using RLS algorithm.
IV.THE ROBOT SERVO CONTROL SYSTEM BASED ON VISION
Six-degree-of-freedom robots have six degrees of freedom,and these industrial robots are implemented by six joints (J1 to J6),respectively.The six joints (J1 to J6) all have a servo motor and a decelerator.A six-degree-of-freedom robot can be regarded as a kinematic chain which is connected by a series of rigid bodies through the joints.The rigid bodies are called connecting rods,and the six-degree-of-freedom robot comprises shoulder joint,upper arm,elbow joint,lower arm,wrist and the end-effector.Fig.2 is a modular and multijointed robot.Forward kinematics and inverse kinematics are two important aspects of robot arm motion analysis,and inverse kinematics is used to obtain the joint angles when the position and posture of the end joint are specified.

Fig.2.A modular and multi-joint robot.
The robot servo control system based on vision consists of a modular and multi-jointed robot,a laser and a camera,the laser is fixed on the J6 joint of the robot,and the camera can obtain the position of laser point as a sensor.Fig.3 is the robot servo control system based on vision.

Fig.3.The robot servo control system based on vision.
The goal of the robot servo control system based on vision is to make the laser point arrive at the designated location.However,the robot servo control system based on vision contains many nonlinear uncertainties,such as,friction torque disturbance,calibration error,etc.Due to nonlinear uncertainties of the robot servo control system based on vision,it is suitable for verifying the effectiveness of the proposed ITF-ORVFL on this system.
In this paper,the position control of the laser point inY-axis direction is adopted,and the position of the laser point inXaxis is a constant value in actual experiments.The state equation of the robot servo control system based on vision is
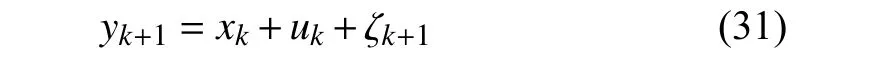
wherexkis the position of laser point at timek,ζk+1andyk+1are the nonparametric uncertainty of this system,the laser point which is obtained by camera at timek+1,respectively,andukdenotes control signal.The nonparametric uncertainty indicates the sum of the nonlinear uncertainties of this system.
The use of forgetting factor in ITF-OELM can accelerate the convergence speed for system identification but may lead to an ill-conditioned covariance matrix in the recursively updating process,ITF-ORVFL also has this issue,and in order to solve this issue,the change detection mechanism is also introduced in ITF-ORVFL.Besides a novel variable is added to the update for mulae of ITF-ORVFL for the purpose of analyzing system stability.
The robot servo control system based on vision is a special system where the training data comes one by one which meansNk=1.ITF-ORVFL is performed in two main stages,the first stage is parameter initialization,and the second stage is parameter learning.
1) Initialization Phase:
a) The parameters of ITF-ORVFL are λ=0.005,ρ=0.998,L=350,M=2,△ =0.0000001,Mm=2000,and η =0.
b) Set ηm=20.When ITF-ORVFL is initialized,ITFORVFL need much training data that is used to train network,the value ηmis important for the change detection mechanism in ITF-ORVFL,and this value can be adjusted based on estimated error.TheMmcan be decided based on actual situation.
c) Assign reference signal.
d) The initialization of ITF-ORVFL is
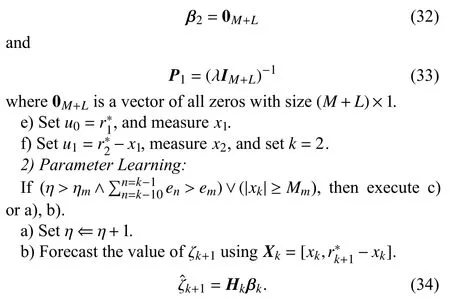
c) Do the work of initialization phase,and set=0,and η=0.
d) Calculateuk,and
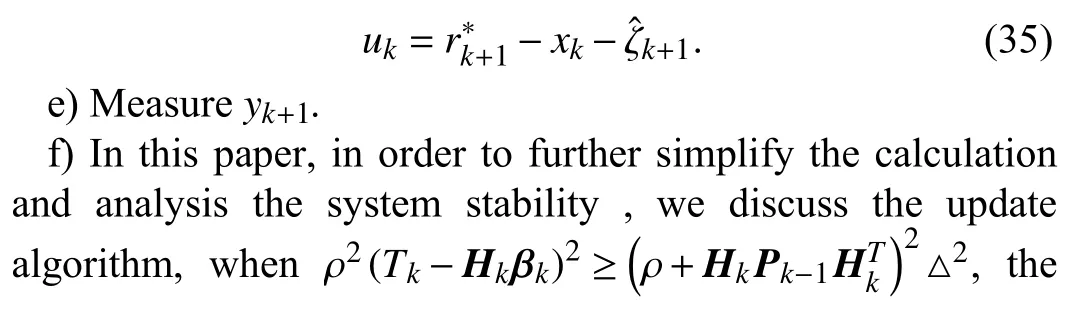

A.Stability Analysis
In this paper,the camera is roughly calibrated,the main part of ζk+1is calibration error,and the ζk+1of this system is considered as a nonlinear function,and it is estimated by ITFORVFL.The RVFL network has the universal approximation capability for a continuous function on a bound finite dimensional set with a closed-form solution.ITF-ORVFL is an online learning algorithm,and it can train RVFL using online data.
Assumption 1:Because of the universal approximation capability of the RVFL network,if enough data is available and the number of enhancement nodes is appropriate,there is β*and
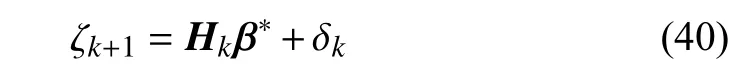
where s up|δk|≤△,and △ is a given upper bound.
In this paper,RVFL is used to estimate the nonlinear functionζk+1,we select the output of the RVFL network as the est imatedvalue of=Hkβk.
Introducing Lyapunov candidate as

Substituting (36) and (37) in (41),we can get that
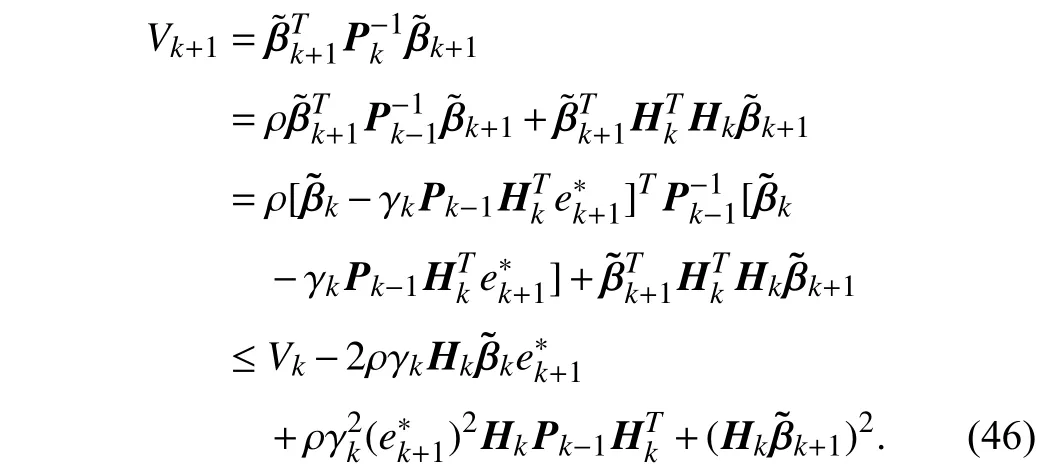
Substituting (45) in the above equation,
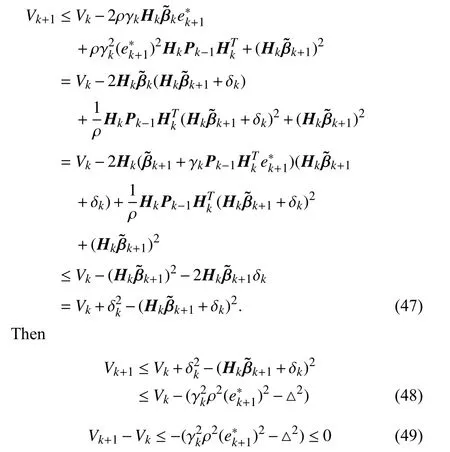
andVk+1is nonnegative.
Based on (49) and (43) and the update algorithm,we can get that

If enoughdataisobtained,based (53),andthe universal approx imati on ability of RFVL net work,we canget will infinite approach β*,that is to say,we can get that

where ε1is very value,so,we also can get the system tracking error will be less than ε1basing on (54) and (35).
V.ANALYSIS OF EXPERIMENT RESULTS
In order to realize the control of uncertain systems with large nonlinear uncertainty,nonparametric uncertainty is estimated by using the input data of systems and the output data of systems,and the required control law is designed based on the estimated value of nonparametric uncertainty.NN is a good class of nonlinear function approx ima tors,and NN has recently received considerable research interests in the identification and control of dynamical systems [20]–[29].
In this paper,the camera is roughly calibrated,ζk+1of the system (28) is considered as a nonlinear function,and two simulation experiments are done.The control algorithm which contains the estimated value of ζk+1by RVFL using the proposed ITF-ORVFL is compared with the control algorithm which contains the estimated value of ζk+1by ITF-OELM and the control algorithm which does not contain the estimated value.In order to describe the control algorithm which does not contain the estimated value easily,this control algorithm is named as DC.
In order to further show the effectiveness of algorithms,the following two indices are introduced: the maximum of |ek|,and the mean value of |ek|.
The maximum of |ek| is
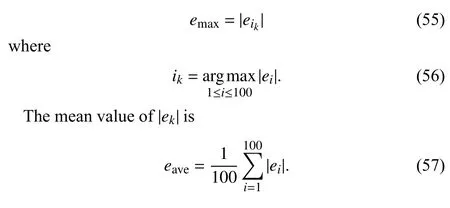
A.The First Experiment
In the first experiment,em= 100,and 100 random points between 318 and 417 inY-axis are generated.Two adjoining random points are different,and those 100 random points are selected as the reference signal.Fig.4 and Fig.5 denote the first experiment results.Figs.4 (a)–(d) are the tracking curves of the control algorithm which contains the estimated value by ITFORVFL,the control algorithm which contains the estimated value by ITF-OELM,DC,and the changing curve of the reference signal,respectively.TheY-axis of Fig.5 indicates the tracking error of experiment 1,and theX-axis of Fig.5 indicates the number of robot arm motion.Fig.5 plots the tracking error curves of the robot servo control system based on vision.The indices ofeaveandemaxare showed in Table I.Fig.5 and Table I show that the control algorithm which contains the estimated value of nonparametric uncertainty by ITF-ORVFL have a higher control accuracy than two other algorithms,when the reference signal is a sequence which contains 100 random points.The results of Fig.5 and Table I imply that ITF-ORVFL is effective coping with nonparametric uncertainty of the system (28),where the reference signals is a sequence which contains 100 random points.
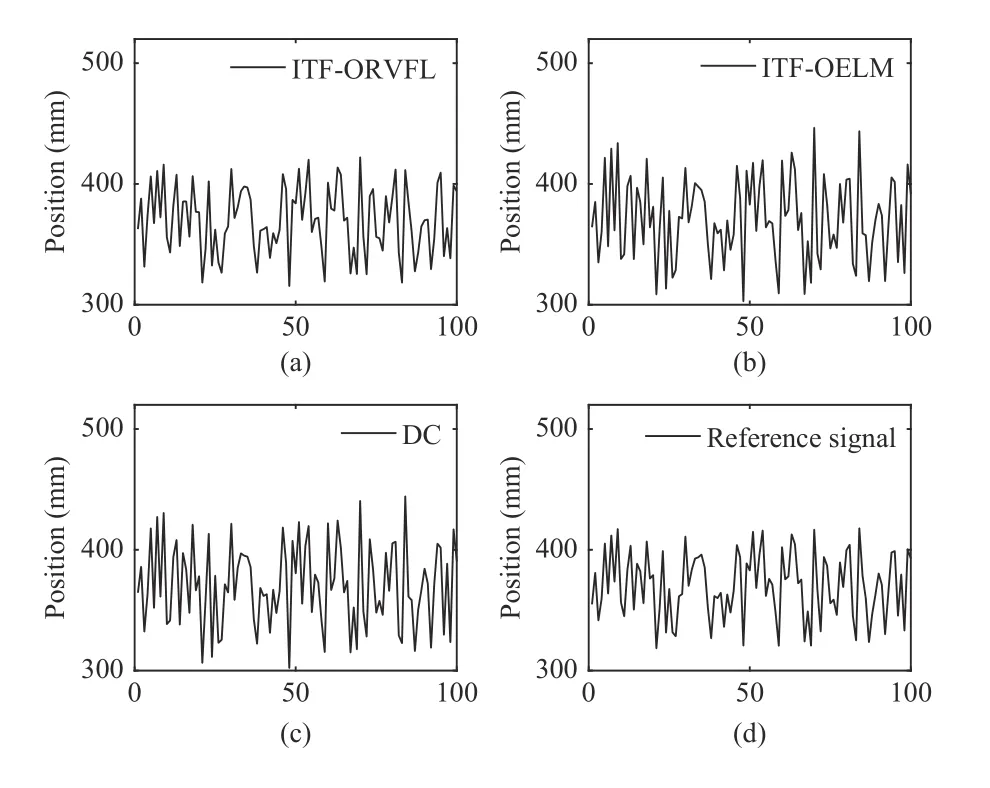
Fig.4.The tracking curves of Experiment 1.(a) The tracking curve of ITFORFVL; (b) The tracking curve of ITF-OELM; (c) The tracking curve of DC;(d) The changing curve of reference signal.
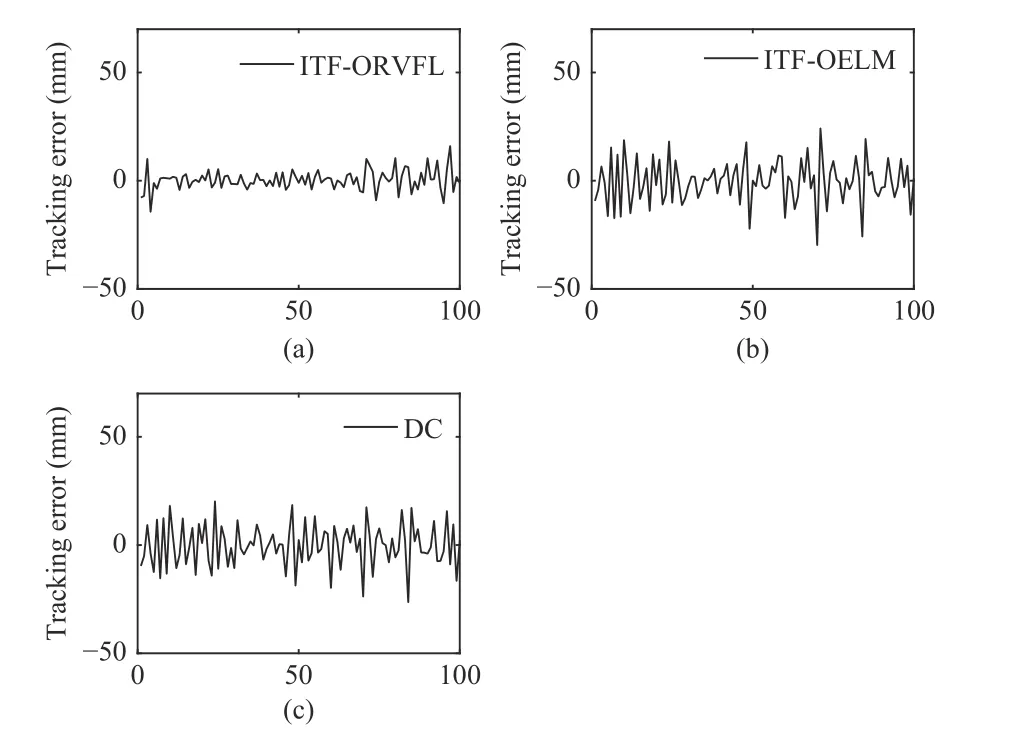
Fig.5.The tracking errors of Experiment 1.(a) The error curve of ITFORFVL; (b) The error curve of ITF-OELM; (c) The error curve of DC.
B.The Second Experiment
In the second experiment,em=12,and the reference signal is

Figs.6 and 7 denote the second experiment results.Figs.6 (a)–(d) are the tracking curves of the control algorithm which contains the estimated value by ITF-ORVFL,the control algorithm which contains the estimated value by ITF-OELM,DC,and the change curve of the reference signal in the secondexperiment,respectively.Fig.7 plots the tracking error curves of the robot servo control system based on vision.Table II show theeaveandemaxindices of the second experiment.The results of Fig.7 and Table II imply that ITF-ORVFL is effective in coping with nonparametric uncertainty of the system (28),when (58) is adopted as reference signal.

TABLE ITHE INDICES OF EXPERIMENT 1
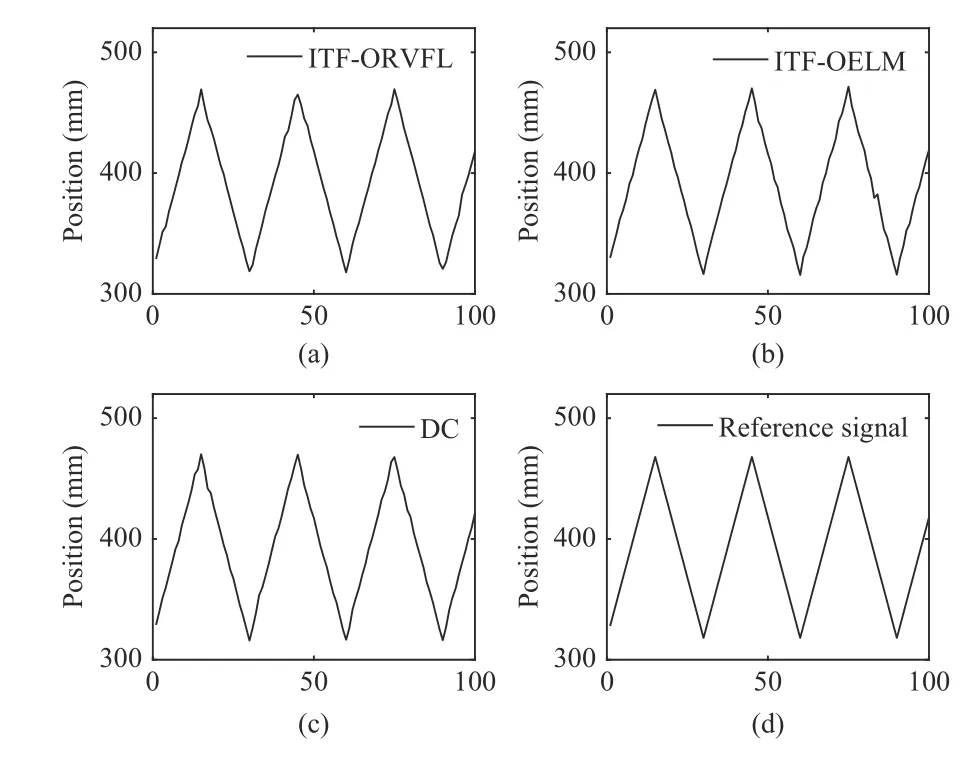
Fig.6.The tracking curves of Experiment 2.(a) The tracking curve of ITFORFVL; (b) The tracking curve of ITF-OELM; (c) The tracking curve of DC;(d) The changing curve of the reference signal.
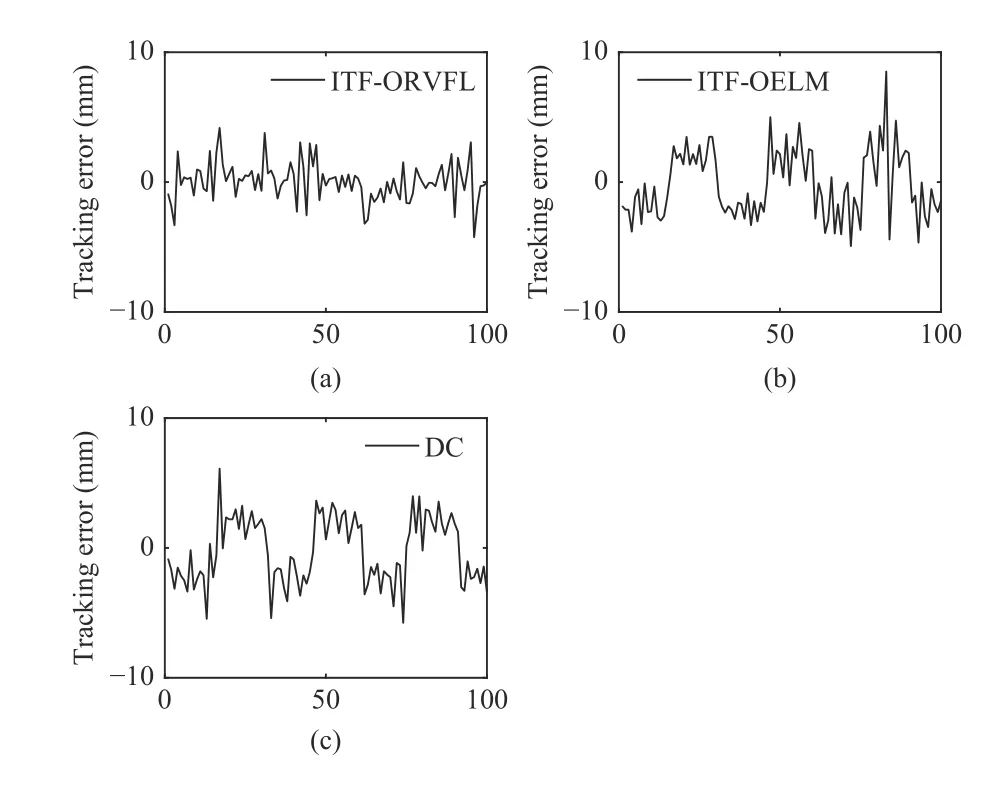
Fig.7.The tracking errors of Experiment 2.(a) The error curve of ITFORFVL; (b) The error curve of ITF-OELM; (c) The error curve of DC.
VI.CONCLUSION
In this paper,inspired by ITF-OELM and BLS,ITFORVFL has been introduced to train RVFL,a novel variable is added to the update for mulae of ITF-ORVFL,a robot servo control system based on vision is adopted to verify the effectiveness of ITF-ORVFL in predicting nonparametric uncertainty of the system.The stability of the proposedalgorithm is guaranteed by theoretical analysis.Two experiments have been performed,and these two experiments show that the proposed ITF-ORVFL algorithm is effective in estimating nonparametric uncertainty of actual systems.

TABLE IITHE INDICES OF EXPERIMENT 2
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Deep Learning Based Attack Detection for Cyber-Physical System Cybersecurity: A Survey
- Sliding Mode Control in Power Converters and Drives: A Review
- Cyber Security Intrusion Detection for Agriculture 4.0: Machine Learning-Based Solutions,Datasets,and Future Directions
- Barrier-Certified Learning-Enabled Safe Control Design for Systems Operating in Uncertain Environments
- Cubature Kalman Filter Under Minimum Error Entropy With Fiducial Points for INS/GPS Integration
- Conflict-Aware Safe Reinforcement Learning:A Meta-Cognitive Learning Framework
