Optimal Synchronization Control of Heterogeneous Asymmetric Input-Constrained Unknown Nonlinear MASs via Reinforcement Learning
2022-01-26LinaXiaQingLiRuizhuoSongandHamidrezaModaresSenior
Lina Xia,Qing Li,Ruizhuo Song,,and Hamidreza Modares, Senior
Abstract—The asymmetric input-constrained optimal synchronization problem of heterogeneous unknown nonlinear multiagent systems (MASs) is considered in the paper.Intuitively,a state-space transformation is performed such that satisfaction of symmetric input constraints for the transformed system guarantees satisfaction of asymmetric input constraints for the original system.Then,considering that the leader’s information is not available to every follower,a novel distributed observer is designed to estimate the leader’s state using only exchange of information among neighboring followers.After that,a network of augmented systems is constructed by combining observers and followers dynamics.A nonquadratic cost function is then leveraged for each augmented system (agent) for which its optimization satisfies input constraints and its corresponding constrained Hamilton-Jacobi-Bellman (HJB) equation is solved in a data-based fashion.More specifically,a data-based off-policy reinforcement learning (RL) algorithm is presented to learn the solution to the constrained HJB equation without requiring the complete knowledge of the agents’ dynamics.Convergence of the improved RL algorithm to the solution to the constrained HJB equation is also demonstrated.Finally,the correctness and validity of the theoretical results are demonstrated by a simulation example.
I.INTRODUCTION
THE input constraint is inevitable in most control systems and it is of vital importance to take it into account when designing controllers for real-world applications,such as cable-suspended robot in [1],wing unmanned air vehicles(UAV) in [2],etc.Implementing the control solutions that ignore the input constraints in the design phase on the inputconstrained systems degrades their performance and it can even make them unstable [3]–[5].
In recent years,the research on control of single-agent systems with symmetric-input constraints has become more and more mature,and sound theoretical results have been reported in [6]–[9].Reference [6] addressed nearly optimal control of input-constrained nonlinear systems using neural networks (NNs).An adaptive optimal constrained-input controller was designed by employing a novel policy iteration(PI) algorithm in [7].An event-triggered optimal controller for a partially unknown input constraint system was presented in[8].Reinforcement learning (RL)-based constrained-input nearly optimal control was studied in [9].An RL-based constrained-input control solution was also developed for discrete-time systems in [10].Constrained-input control solutions were also analyzed for single-agent systems affected by external disturbances [11],[12].Further,the achievement on input saturation control of discrete-time nonlinear systems with unknown nonlinear dynamics was made under stochastic communication protocols (SCPs) in [13].The solution to the adaptive NN control problem for discrete-time nonlinear systems under input saturation was also presented by a multigradient recursive RL scheme [14].
Actually,many nonlinear plants suffer from asymmetricinput constraints in engineering industries.Fortunately,there is some literature available on asymmetric-input constraint problems.A smooth continuous differentiable saturation model was investigated to tackle the asymmetric constrainedinput control problem for a class of nonlinear systems in [15],while its optimization for system is not guaranteed.Reference[16] developed an adaptive asymmetric bounded control scheme for uncertain robots through introducing a switching function.Notably,obtaining such a function is quite challenging due to the nonlinearity of the system.More recently,by a modified hyperbolic tangent function,[17]presented an optimal asymmetric critic-only control method for certain nonlinear systems,and further discussed the stability of the closed-loop system,which was regarded as a supplement and theoretical extension of the obtained result in[18].However,it requires the dynamics information of the system which may be not available in many real-world applications.More importantly,the aforementioned results are limited to nonlinear single-agents.
Nevertheless,input constraints are also present in multiagent systems (MASs).MASs involve interaction and collaboration between agents to achieve a common goal[19]–[21],or track a given trajectory [22]–[24],or complete containment and formation tasks [25]–[27].The distributed nature of the control solutions for MASs has exacerbated the design of constrained-input controllers for them,as the control input of each agent depends on not only its own state information but also those of its neighbors.For second-order MASs subject to input constraints,the consensus problem with both velocity and input constraints was analyzed in [28].Reference [29] presented a non-convex constrained consensus controller for heterogeneous higher-order MASs with switching graphs.Reference [30] addressed the leader following constrained cooperative control problem of homogeneous nonlinear MASs.The optimal consensus control design was investigated for heterogeneous MASs with symmetric input constraints [31].As aforementioned,the designed controls either ignore the optimality of the distributed solution or are restricted to systems with no input constraints or at best symmetric-input constraints.Moreover,their applications are also limited to homogeneous MASs.To circumvent these issues,it is desirable to investigate an asymmetric input constraint strategy to solve the optimal control problem for heterogeneous nonlinear MASs,which motivates our investigation.
Adaptive dynamic programming (ADP) algorithms,which are developed on the basis of dynamic programming [32],have been widely used to deal with optimal control of uncertain systems,such as path following for underactuated snake robots [33],of which PI is a branch [34]–[36].Interestingly,ADP and RL are two interchangeable names[17],where [37] and [38] introduced that RL algorithms solve the control problem of gene regulatory network and the adaptive fault-tolerant tracking control problem of discretetime MASs,respectively.The reader is referred to literature[39],[40] for more information on RL.In the design of constrained-input optimal controllers,model-based PI was commonly employed to solve a nonquadratic Hamilton-Jacobi-Bellman (HJB) equation in [6],[41],[42] with exact dynamics information of systems.To obviate the requirement of the complete knowledge of the system’s dynamics,[8]proposed an identifier-critic-actor structure to learn the solution to HJB equation for partially-unknown symmetric constrained-input single agent.Reference [43] gave the integral RL and experience replay method to solve the symmetric constrained-input optimal control problem for partially-unknown systems.And then,some researchers also leveraged model-based PI based on learning the system dynamics for unknown constrained-input single-agent in [7],[44].However,in most situations,the addition of model NN increases the complexity of the architecture correspondingly,and there exists a small modeling error,since NNs cannot match the unknown nonlinear systems exactly.
To overcome the aforementioned shortcomings of the existing results,in this paper,we develop an asymmetric constrained-input optimal control scheme for heterogeneous unknown nonlinear MASs.First,a state-space transformation is performed to deal with asymmetric input constraints.Then,a nonquadratic cost function is constituted such that the input constraints are encoded into optimization problem.After that,an improved data-based and model-free RL algorithm is presented to learn the solution to the constrained HJB equation,without requiring system’s dynamics information.Furthermore,convergence of the proposed algorithm is also shown.The main contributions are as follows.
1) We present a state space transformation method to solve the optimal synchronization control problem for heterogeneous nonlinear MASs with asymmetric input constraints.In addition,it implies that the symmetric input constraints in relevant work can be regarded as a special case of our research work.
2) An improved data-based RL algorithm is employed to learn the solution to the non-quadratic HJB equations without requiring system’s dynamics information.To implement this algorithm,the critic NN and the actor factor NN are established respectively,instead of the actor NN in [45]–[47],to estimate the cost function and the control policy for agents,such that input constraint is encoded into the framework of the proposed algorithm.Whereas,the control signal with input constraints cannot be approximated by actor NN in [45]–[47],since it fails to reflect the amplitude limit of the control input.
The remaining sections are organized as follows.The asymmetric input-constraints synchronization problem is formulated in Section II with some knowledge of graph theory.Section III gives the result of problem transformation.For nonlinear leader,a novel distributed observer is designed in Section IV.The optimal asymmetric input-constrained controller is acquired in Section V.Section VI proposes an improved data-based off-policy RL algorithm and its implementation for solving non-quadratic HJB equations.In Section VII,a simulation example is given to verify the correctness and effectiveness of the improved algorithm.Section VIII draws the conclusions.
Notations:Rn1×n2stands for the set of alln1×n2real matrices.The symbolsAT,A-1,and λmin(A) are the transpose,inverse,and minimum eigenvalue of the matrixA∈Rn×n.Define col(a1,...,aN)=,withai∈Rni,i∈{1,...,N},withamaxbeing the maximum element.Let diag(a1,...,aN) be a diagonal matrix with scalarsai,i∈{1,...,N}being the diagonal elements.The Kronecker product is denoted as the symbol ⊗.The symbol 1nis anndimensional vector with all elements 1.The identity matrix of dimensionN×Nis given byIN.
II.PROBLEM STATEMENT
A directed graphG(Π,Γ,A) consists ofNfollower nodes,where a nonempty finite node set is denoted as Π ={κ1,κ2,...,κN} and the edge set is Γ ⊆Π×Π.A=[aij] is referred to the adjacency matrix,ai j=1 indicates that there is a directed edge from nodejtoi; otherwise,ai j=0.The Laplacian matrix is represented asL=diag-Awithaii=0.The pinning gain matrix illustrates the connection between the leader node κ0and the follower node κi,i∈{1,2,...,N} inΠ,denoted as Ψ =diag(ψ1,ψ2,...,ψN),ψi=1 implies the existence of a directed edge from node κ0to κi; otherwise,ψi=0.
Consider the dynamics of asymmetric input-constrained heterogeneous nonlinear followers as

whererepresents thek-th control signal foruiwithk∈{1,2,...,mi},the saturating bounded actuators are denoted as αiand βi.
The dynamics of the nonlinear leader is described by
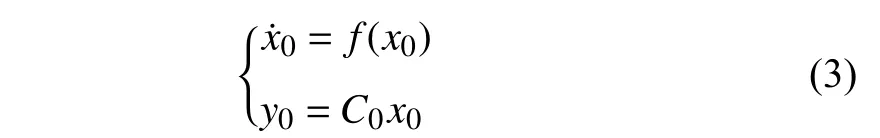
wherex0∈Rnis the state of the leader,f(x0)∈Rnis the drift dynamics,andy0∈Rpis the output.C0∈Rp×nis the output matrix of the leader.
Before proceeding,the following assumptions are introduced.
Assumption 1:The augmented directed graph()consisting ofNfollower nodes and one leader node contains a s panning tree with the root being the leader node κ0,where.
Assumption 2:fi(xi)+gi(xi)uiis Lipschitz continuous on a set Ω ∈Rni,and the followers are stabilizable.In addition,f(x0) is Lipschitz continuous withf(0)=0.
Assumption 3:The saturating bounded actuators αiandβiare known with αi<βi.
Next,the optimal synchronization control problem is formulated for heterogeneous nonlinear MASs with asymmetric input-constrained.
Problem 1:Consider the heterogeneous nonlinear MASs with (1) and (3).Design a controluisuch that the output synchronization problem for heterogeneous nonlinear MASs subject to asymmetric input-constrained is solved.That is
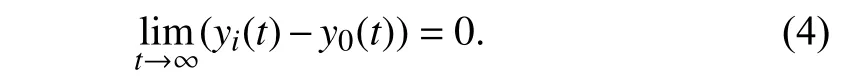
Remark 1:Unlike most of the previous work in [6],[30],[31],which considered symmetric input constraints in form of,with λibeing a positive constant,the asymmetric input-constraints problem is explored in this paper with.Therefore,new theoretical developments are required to account for asymmetric input constrains.
III.PROBLEM TRANSFORMATION
To achieve the asymmetric input-constrained synchronization problem of heterogeneous nonlinear MASs,this section presents new results.
Problem2:Design acontrolηiforthe following trans for-med system with symmetric input-constrainedsuch that the synchronization condition (4) holds.
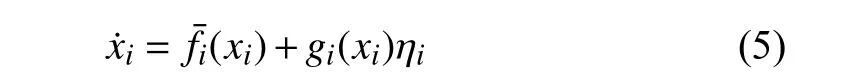
The following theorem gives the relationship between Problems 1 and 2.
Theorem 1:Problems 1 and 2 are equivalent if the functionand the signal ηisatisfy the following conditions:

whereriis a constant and satisfiesri=(αi+βi)/2,and 1miis anmi-dimensional vector with all elements1.
Proof:The control signalin (2) is processed as foll?ows:
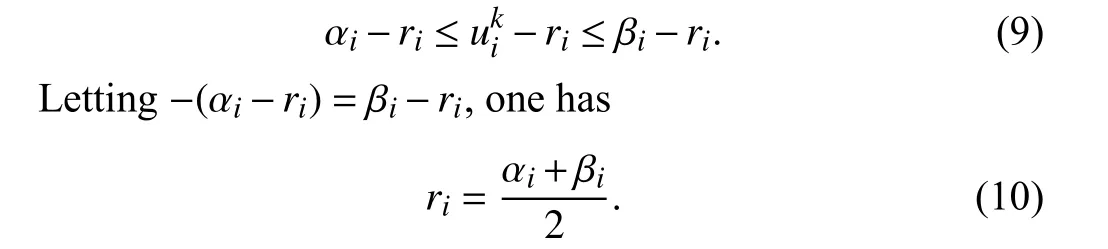
Next,invoking (6) and (7),the follower dynamics in (1) can be rewritten as

IV.THE DESIGN OF NOVEL DISTRIBUTED OBSERVER
In scalable networks of MASs,the communication is assumed to be sparse and thus some followers do not have access to the leader’s information.In this context,some of the previous work in [48]–[50] on synchronization problem is confined.In this section,for heterogeneous nonlinear MASs,a novel distributed observer for each follower is investigated to estimate the state of the leader.
Define the disagreement vectoreias
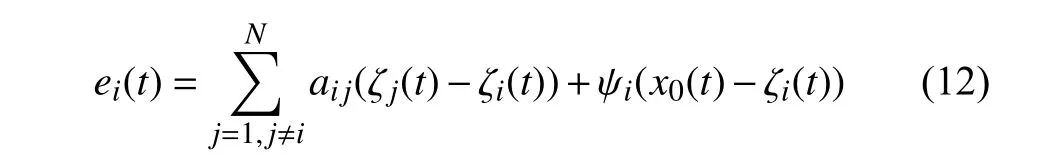
where ζi∈Rnand ζj∈Rnare the states of observer i and its neighbor, respectively.
Then,the observer is represented as

wherek1is a constant to be determined later,ei(t) is given in(12).Now,we define the state observer error as

where ρ0is the Lipschitz constant off(·) ,φmaxdenotes the maximum element of φ=col(φ1,φ2,...,φN).Define Λ=(Φ(L+Ψ)+(L+Ψ)TΦ)/2,and the minimum eigenvalue of Λ is indicated as λmin(Λ).
Proof:Both the leader in (3) and the observer in (13) are described in a compact form,respectively,as

Using (15) and (19),the derivative of (20) is
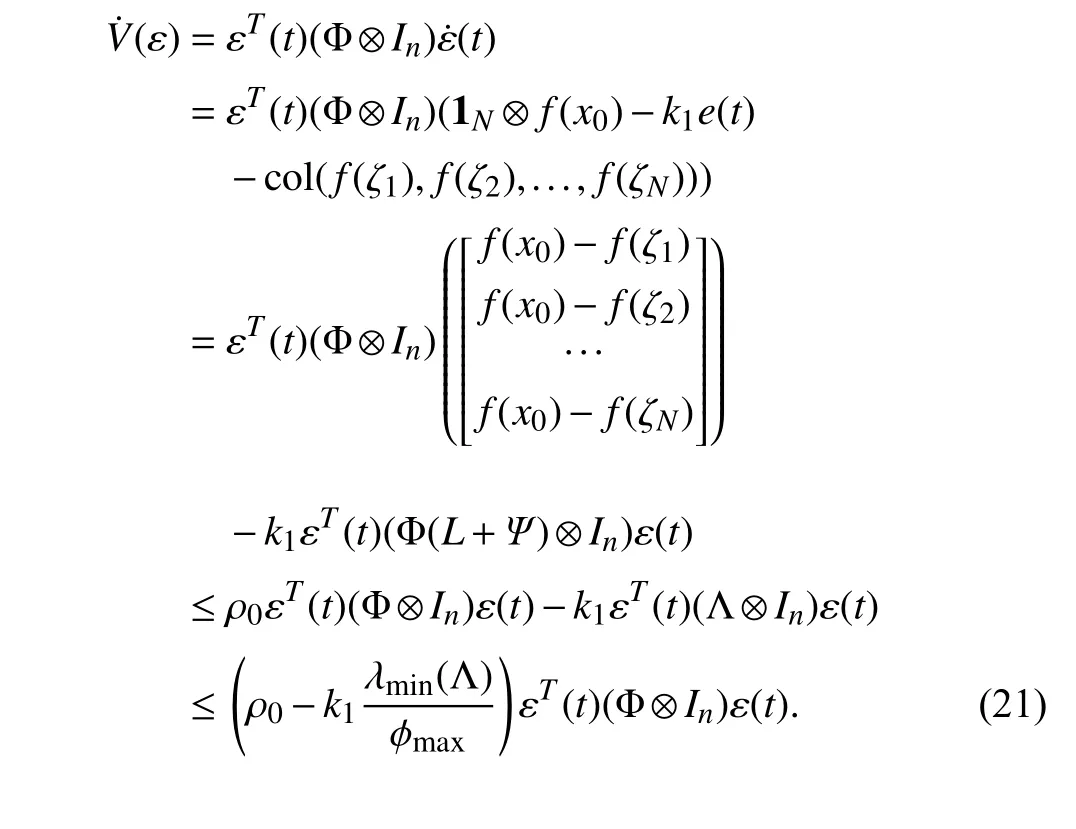
Based on (21),if the parameter satisfiesk1≥ρ0φmax/λmin(Λ),then,(t)<0.
V.THE OPTIMAL INPUT-CONSTRAINED CONTROLLER
In this section,the optimal input-constrained controlleris designed for followers.Firstly,a nonquadratic cost function is leveraged to incorporate the agents’ input constraints.After that,an optimal controller is obtained by minimizing the cost function,and then the feasibility of the controller is confirmed.
The augmented state of the follower in (5) and the observer in (13) is presented by
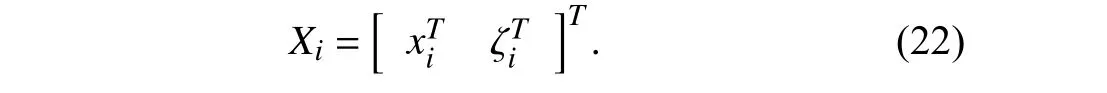
Then,the dynamics of the augmented system is derived by
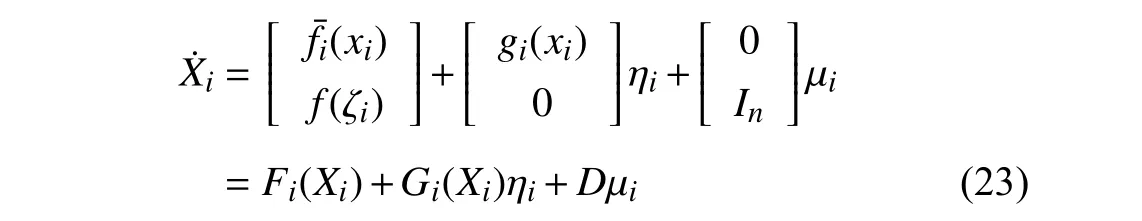
where the signal denotes μi=k1ei.
Define the nonquadratic cost function for thei-th follower as

Using integration by parts,the formula (25) can be rewritten as
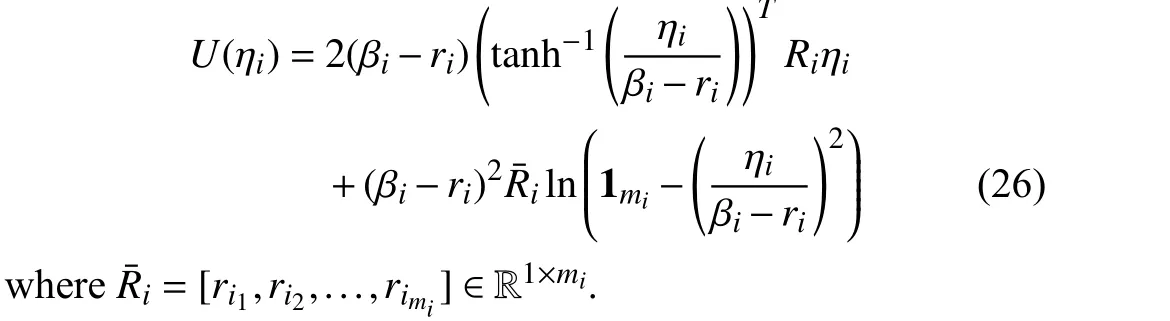
Differentiating the cost function (24) along the system (23)yields
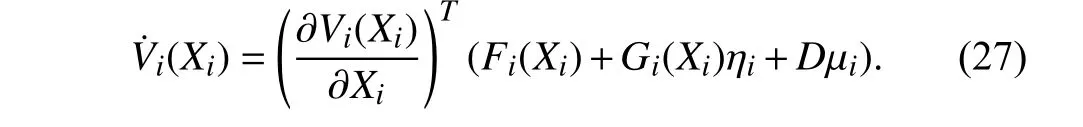
Invoking (25),we further obtain
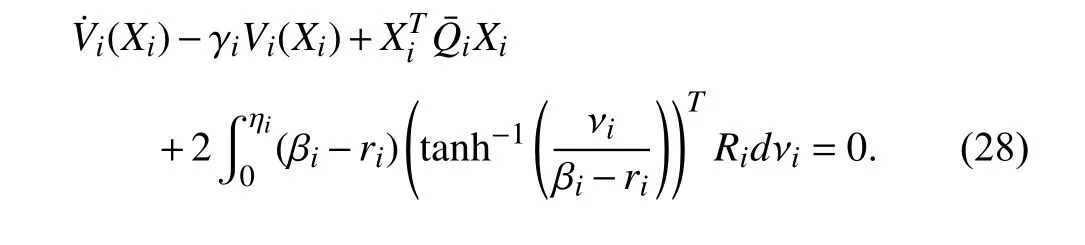
The optimal input-constrained controllersatisfies
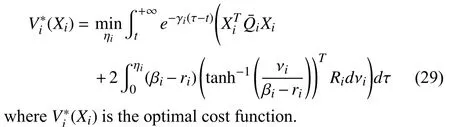
Using (27) and (28),the Hamiltonian function is defined for followers by

Substituting (31) and (32) into (30) yields the following nonquadratic HJB equation for finding the optimal value function.

where the optimal controlleris derived in (31) by minimizing the cost functionVi(Xi(t)) in (24).
Select the Lyapunov function as
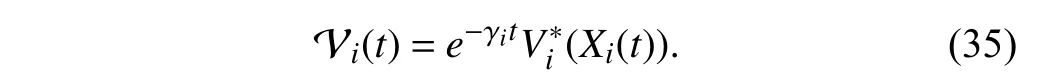
Using (27),the derivative of (35) with respect to time is
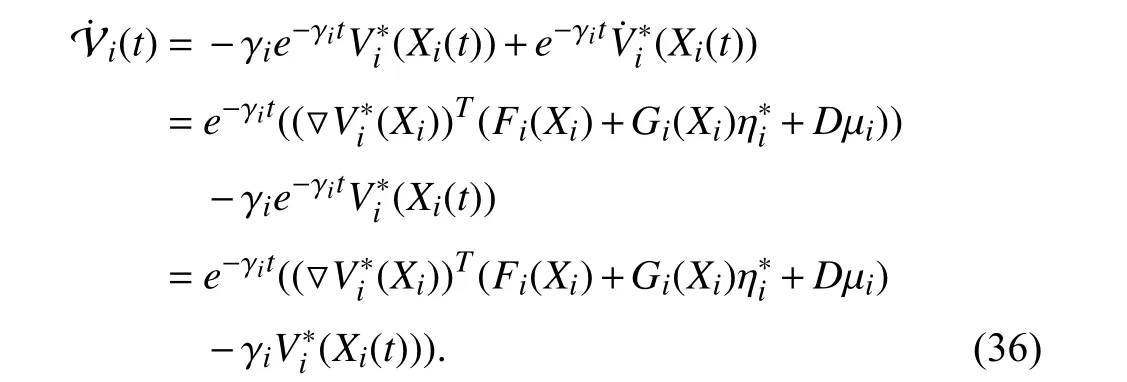
Invoking (33),the formula (36) can be rewritten as

The nonquadratic HJB equation in (33) is extremely difficult to solve in the form of analytic solution due to the nonlinearity of the MASs and the limitation of the control input.In the next section,an improved data-based RL algorithm is investigated to solve the constrained HJB equation.
Remark 2:Unlike [16],which introduced a switching function to solve the problem of asymmetric input constraints,we propose a state space transformation method to solve the asymmetric input constraint optimal synchronization control problem for heterogeneous nonlinear MASs,obviating the difficulty of constructing the switching function.An important difference from [17] is that we propose an asymmetric optimal control strategy for nonlinear heterogeneous MASs rather than nonlinear single-agent systems.
VI.THE IMPROVED DATA-BASED OFF-POLICY RL FOR SOLVING HJB EQUATION
In this section,an offline PI algorithm for solving nonlinear HJB equation in (33) is firstly introduced,which depends on the system model.To optimize this algorithm,partly inspired by [5],[52]–[54],an improved data-based off-policy RL is proposed to solve the synchronization problem of the input constrained nonlinear MASs with unknown dynamics information,and then,the convergence of the two algorithms is also given.Finally,two NNs for each follower are employed to approximate the cost functionVi(Xi) and control factorPi,respectively,to implement the improved data-based off-policy RL algorithm.
A.Offline PI Algorithm
A model-based offline PI algorithm is presented in Algorithm 1 by iterating on 1) the Bellman equation (38) to perform policy evaluation and 2) the policy update (39) to perform policy improvement.



Remark 3:Algorithm 1 requires complete information of the system and thus has limitations in applicability.References [7],[8] employ NN to model the system,avoiding the shortcoming that the algorithm needs complete information of followers,however,compared with the databased off-policy RL algorithm proposed next,the number of NNs increases,which further increases the computational complexity and error sources.
B.An Improved Data-Based Off-Policy RL Algorithm
We extend the results of the previous work [5],[52] and propose an improved data-based off-policy RL algorithm that can tackle the optimal synchronization control problem of heterogeneous unknown nonlinear MASs with asymmetric input-constrained.The overall structure diagram of the proposed result is shown in Fig.1,the critic NN and the actor factor NN are given to estimate the optimal cost function and the control factor respectively,given in next subsection,and then the optimal controllerof the MASs is obtained by a hyperbolic operation tanh(·) and an appropriate translation transformation.
The augmented system in (23) is equivalent to

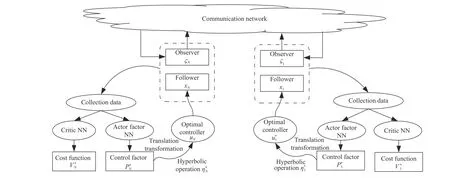
Fig.1.The overall structure diagram.
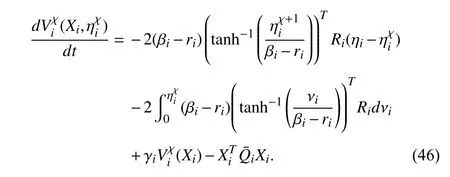
For (46),multiplying both sides by exp(-γi(t-τ)) and integrating over the interval [t,t+ΔT],we have

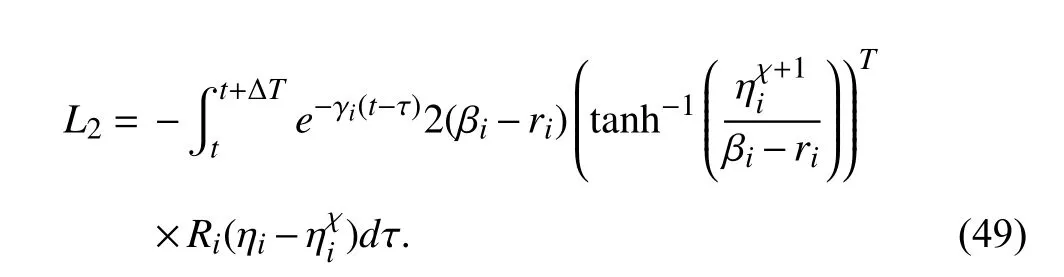
Using (45),the left-hand side of (47) is treated as follows
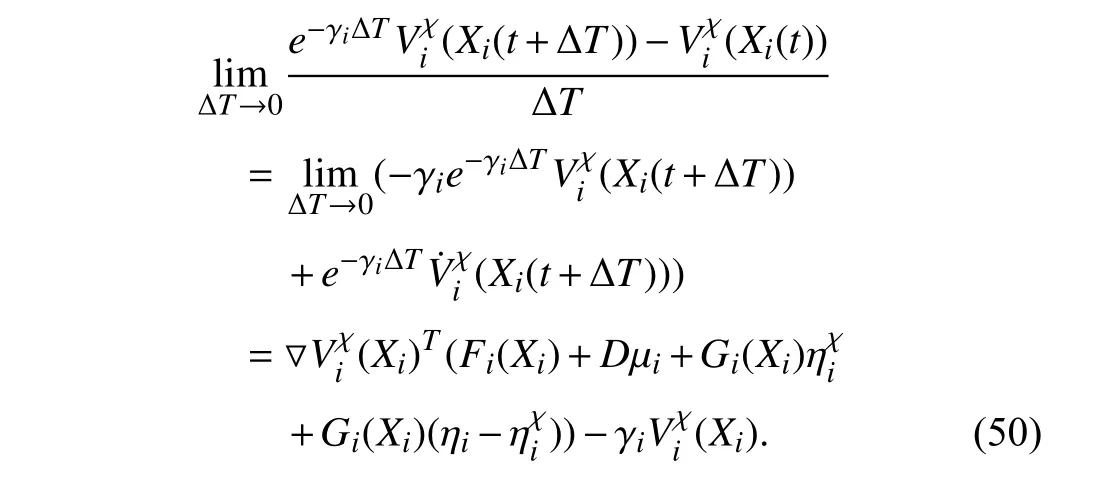
Similarly,the right-hand side of (47) is


C.The Implementation for Data-Based Off-Policy RL Algorithm

Taking (53)–(55) into the integral input-constrained HJB equation (47) gets

Remark 5:It is noted that an admissible control ηiis required in Algorithm 2.Let’s take the followerias an example of how to obtain an admissible control with no information about the system dynamics.If the dynamics of thei-th follower is known to be stable in advance,then the admissible control can be selected as ηi=0; Otherwise,partial information of the system dynamics,Fi(Xi),is required to obtain admissible control.Assume that the dynamics of the augmented system in (23),that is,Fi(Xi),can be linearized to Υiat certain equilibrium points and be further represented by a nominal model ΥNiwith an additive perturbation Δ ΥNi,which is expressedasΥi=ΥNi+ΔΥNi.Then,an admissible control canbe obtained by robust control techniques,suchasH∞control,without requiring any knowledge of the system dynamics.More information is referred to literature [5] and[56],[57].Another method for obtaining an initial admissible control without system dynamics is described in Algorithm 1 of [58],which is limited in space and will not be repeated.
Remark 6:The complexity of the framework is also provided.In terms of time complexity,Algorithm 1 uses only one critic NN,with time complexity beingO(n),wherendenotes the number of iterations,while the proposed Algorithm 2 uses two NNs,namely the actor factor NN and the critic NN,with time complexity beingO(n2),but without requiring the dynamics information of the system.Even though the time complexity of critic neural network (CNN)-based structure modified hyperbolic tangent function method in [17] isO(n),similar to Algorithm 1,which also needs the dynamics information of the system.Therefore,it is worth of further study to avoid the need of the dynamics information of the system while reducing the time complexity.
VII.SIMULATION
In this section,the exploitability and effectiveness of the improved data-based RL algorithm for input-constrained MASs are illustrated by a simulation example.Furthermore,a comparison with CNN-based structure modified hyperbolic tangent function method for solving the asymmetric input-constrained optimal control problem in [17] is given.The network topology is shown in Fig.2.
The dynamics of the agents are governed by
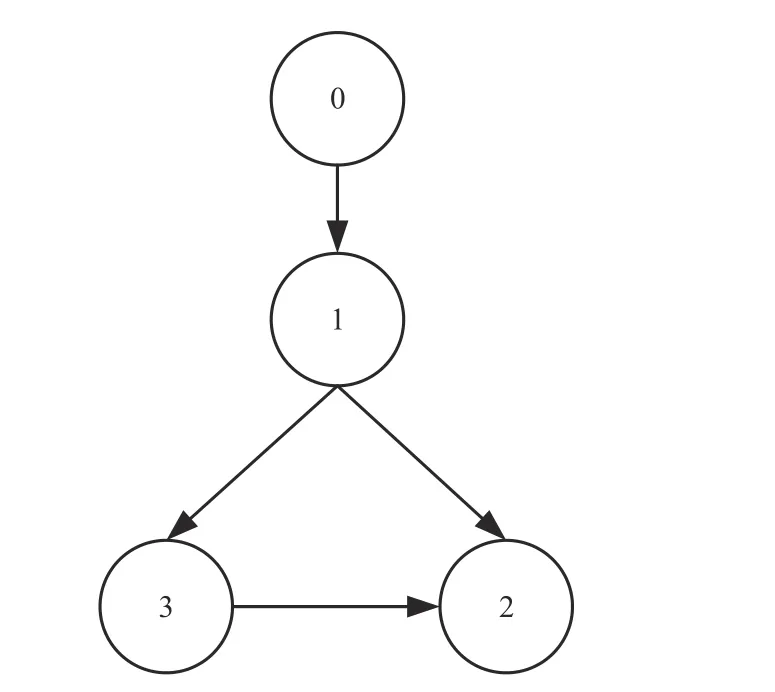
Fig.2.The network topology of multi-agent systems.
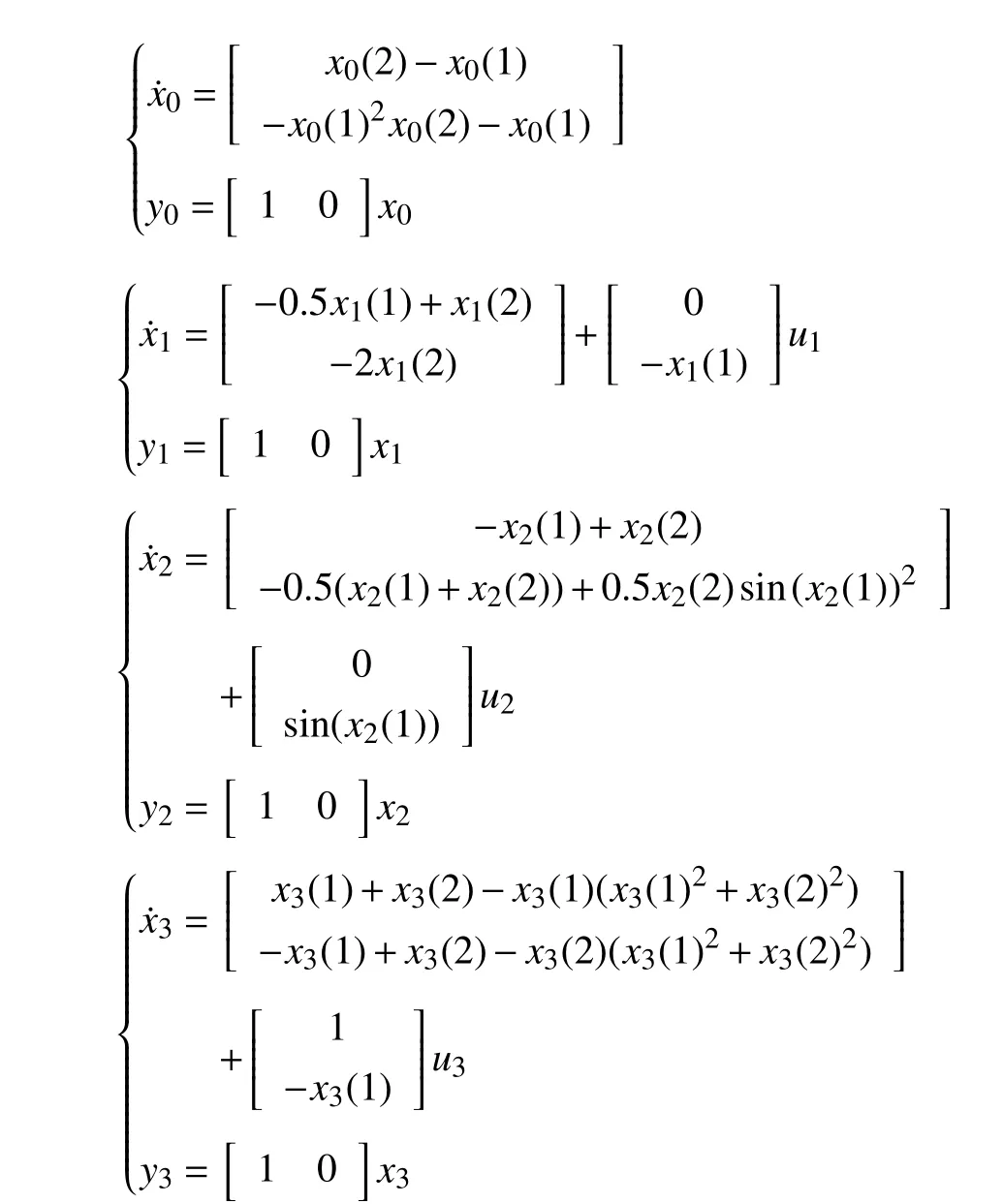
where - 1 ≤u1≤3,- 3 ≤u2≤4,and - 1 ≤u3≤-1.
Based on Theorem 1,we obtain that the translation values of followers arer1=1,r2=0.5 andr3=0.And then,|ηi|≤λi,i∈{1,2,3} is derived with λ1=β1-r1=2 ,λ2=β2-r2=3.5,and λ3=β3-r3=1.
The observer parameter is selected ask1=6.The synchronization results of the states of the observer and the leader are shown in Fig.3.The results of output tracking synchronization between agents by utilizing Algorithm 1 are represented in Fig.4.
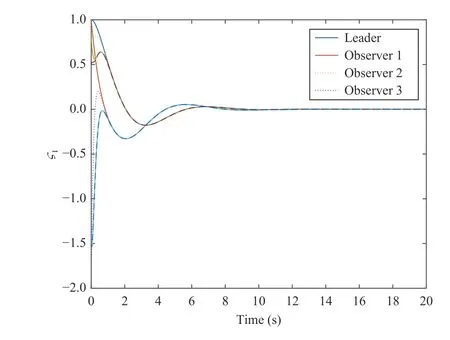
Fig.3.The synchronization results of the states of the observer and the leader.

Fig.4.The results of output tracking synchronization between agents under Algorithm 1.

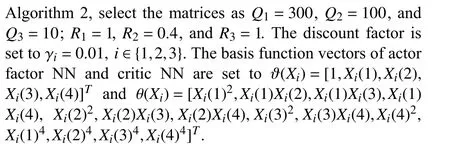
The corresponding actor factor NN constant weight for each follower is obtained as

Under Algorithm 2,the constant weight iterative convergence graphs of the actor factor NN and critic NN are shown in Figs.5 and 6.The constant weight iterative error graphs of the actor factor NN and the critic NN are expressed in Figs.7 and 8.The outputs of agents are displayed in Fig.9.Reference [17] proposed a CNN-based structure modified hyperbolic tangent function method to learn the solution to HJB equation with asymmetric input constraints,where criticonly NN is employed.Figs.10 and 11 show the weight iterative error of the critic NN and the output results of agents under CNN-based structure modified hyperbolic tangent function method.
From the state synchronization results shown in Fig.3,it can be seen that the states of the leader can be accurately estimated by the designed observer in about 2 s,which implies that the observer design in Theorem 2 is available.See Figs.4 and 9,both Algorithms 1 and 2 can effectively make the outputs of followers track that of the leader.The curves in Figs.5 and 6 demonstrate that the constant weights of the actor factor NN and critic NN tend to converge after 10 s.Accordingly,Figs.7 and 8 illustrate that it takes about 10 s for the constant weight iteration errors of the two NNs in (53) and(54) to quickly approach zero.For comparison,it is seen from Figs.9 and 10 that the constant weight iterative error for each follower approaches to zero and the output synchronization is achieved after 40 s by CNN-based structure modified hyperbolic tangent function method in [17].
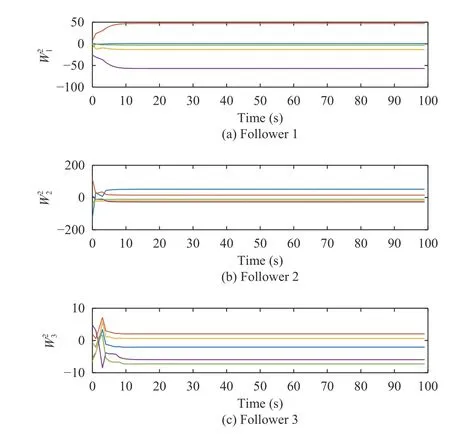
Fig.5.The constant weight iterative convergence graphs of the actor factor NN under Algorithm 2.
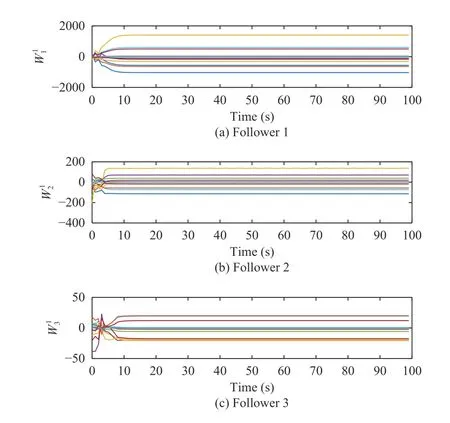
Fig.6.The constant weight iterative convergence graphs of the critic NN under Algorithm 2.
Comparison 1 (Algorithm 1 and Algorithm 2):By comparing the synchronization rate of Algorithms 1 and 2,it can be seen from Figs.4 and 9 that Algorithm 2 is slightly faster than Algorithm 1.Algorithm 1 uses only one critic NN,while Algorithm 2 uses two NNs,namely the actor factor NN and the critic NN.However,no system dynamics information in Algorithm 2 is required.Moreover,Algorithm 1 is an offline policy algorithm run a priori to obtain a neural network constrained state feedback controller that is nearly optimal,whereas the improved Algorithm 2 is presented to learn online the solution to the associated HJB equation without requiring the dynamics of agents.
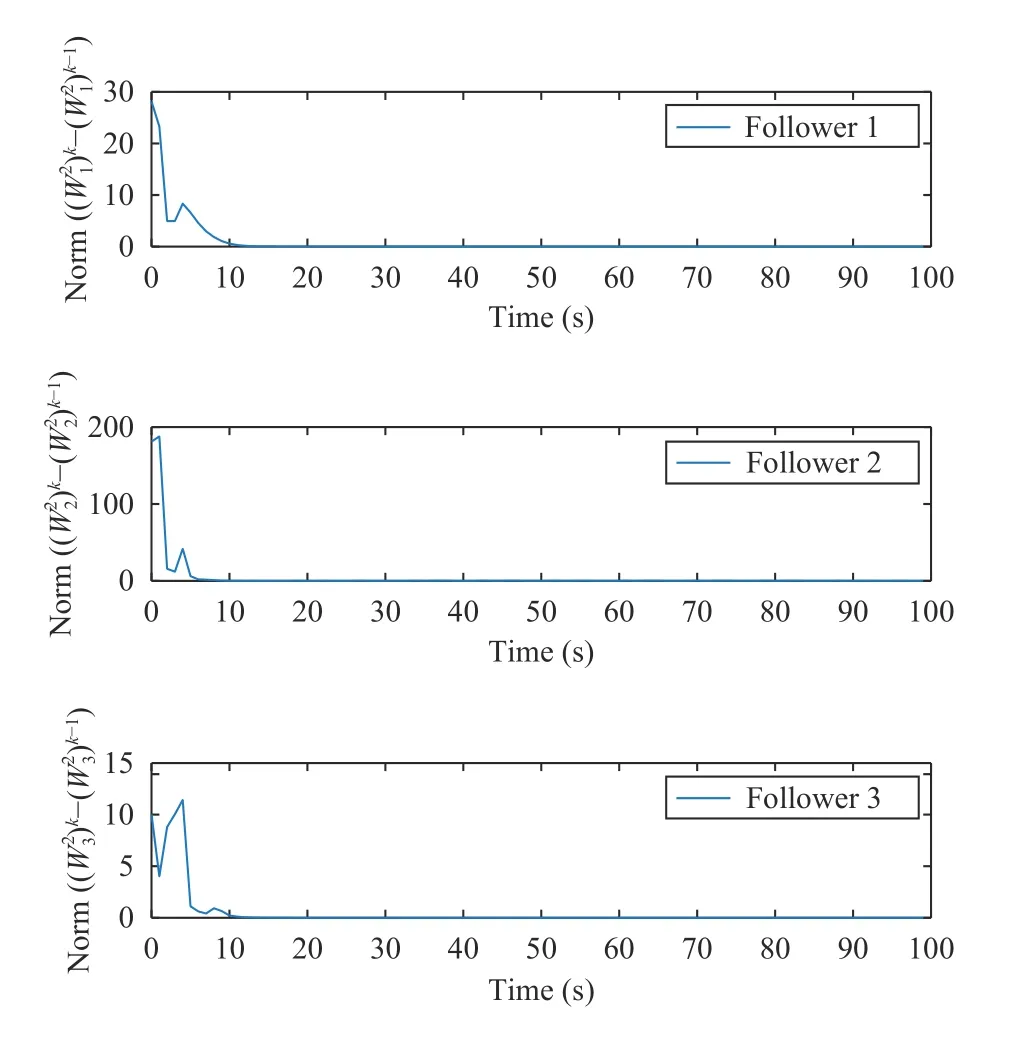
Fig.7.The constant weight iterative error graphs of the actor factor NN under Algorithm 2.

Fig.8.The constant weight iterative error graphs of the critic NN under Algorithm 2.
Comparison 2 (Algorithm 2 and CNN-Based Structure Modified Hyperbolic Tangent Function Method in [17]):
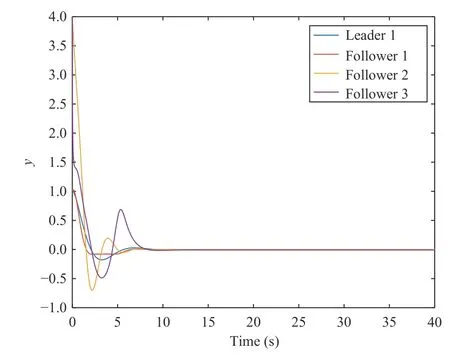
Fig.9.The outputs of agents under Algorithm 2.
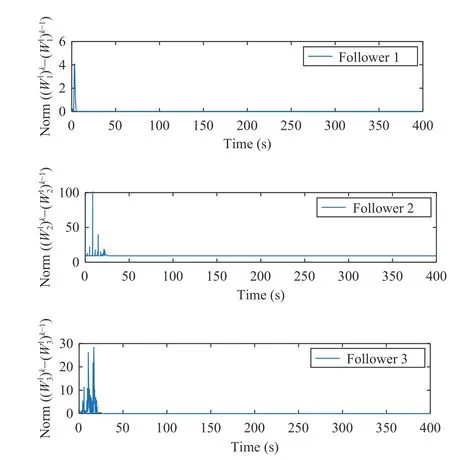
Fig.10.The constant weight iterative error graphs of the critic NN under CNN-based structure modified hyperbolic tangent function method in [17].
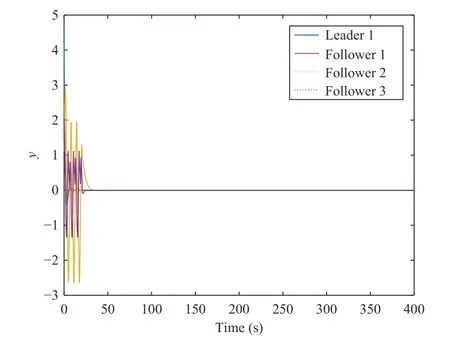
Fig.11.The outputs of agents under CNN-based structure modified hyperbolic tangent function method in [17].
Comparing the convergence rate of constant weights of critic NN between Algorithm 2 and CNN-based structure modified hyperbolic tangent function method,see Figs.8 and 10,Algorithm 2 is obviously faster than CNN-based structure modified hyperbolic tangent function method.It implies from Figs.9 and 11 that the synchronization rate of Algorithm 2 is about 30 s faster than that of CNN-based structure modified hyperbolic tangent function method in [17].Similarly,CNNbased structure modified hyperbolic tangent function method uses critic-only NN,while Algorithm 2 uses two NNs.However,similarly to Algorithm 1,the system dynamics information is still required under CNN-based structure modified hyperbolic tangent function method,and the satisfaction of persistently exciting (PE) condition also needs to guarantee.
Thereupon,the effectiveness of the improved data-based RL algorithm proposed in this paper is verified.
VIII.CONCLUSIONS
The optimal solution to the output synchronization problem of heterogeneous unknown nonlinear MASs with asymmetric input-constrained is proposed in this paper.First,the transformation of the problem is performed by transforming the control input.Then,based on the fact that not every follower can get the state information of the leader,an observer is designed for each follower to predict its state.After that,a cost function with non-quadratic form is established,and the optimal controller is obtained by minimizing it.We propose an improved data-based RL algorithm to apply the synchronization problem of asymmetric input-constrained heterogeneous unknown MASs and compare it with conventional PI algorithm.By implementing the improved RL algorithm,the critic NN and the actor factor NN are constructed respectively to approximate the cost function and control factor.Finally,the effectiveness of the proposed algorithm is verified by a simulation example.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Deep Learning Based Attack Detection for Cyber-Physical System Cybersecurity: A Survey
- Sliding Mode Control in Power Converters and Drives: A Review
- Cyber Security Intrusion Detection for Agriculture 4.0: Machine Learning-Based Solutions,Datasets,and Future Directions
- Barrier-Certified Learning-Enabled Safe Control Design for Systems Operating in Uncertain Environments
- Cubature Kalman Filter Under Minimum Error Entropy With Fiducial Points for INS/GPS Integration
- Conflict-Aware Safe Reinforcement Learning:A Meta-Cognitive Learning Framework
