Full-State-Constrained Non-Certainty-Equivalent Adaptive Control for Satellite Swarm Subject to Input Fault
2022-01-26ZhiweiHaoXiaokuiYueHaoweiWenandChuangLiu
Zhiwei Hao,Xiaokui Yue,Haowei Wen,and Chuang Liu,
Abstract—Satellite swarm coordinated flight (SSCF) technology has promising applications,but its complex nature poses significant challenges for control implementation.In response,this paper proposes an easily solvable adaptive control scheme to achieve high-performance trajectory tracking of the SSCF system subject to actuator efficiency losses and external disturbances.Most existing adaptive controllers based on the certaintyequivalent (CE) principle show unpredictability and non-convergence in their online parameter estimations.To overcome the above vulnerabilities and the difficulties caused by input failures of SSCF,this paper proposes an adaptive estimator based on scaling immersion and invariance (I&I),which reduces the computational complexity while improving the performance of the parameter estimator.Besides,a barrier Lyapunov function(BLF) is applied to satisfy both the boundedness of the system states and the singularity avoidance of the computation.It is proved that the estimator error becomes sufficiently small to converge to a specified attractive invariant manifold and the closed-loop SSCF system can obtain asymptotic stability under full-state constraints.Finally,numerical simulations are performed for comparison and analysis to verify the effectiveness and superiority of the proposed method.
I.INTRODUCTION
FLOURISHMENT of space engineering since the 1960s has given rise to a quantum leap forward of human civilization.The space unmanned systems (SUSs) are intelligent on-orbit systems that perform specific tasks autonomously without human intervention through advanced control and communication technologies.In general,space stations,space robots,satellites,etc.fall under the category of SUSs.Among them,satellites in the form of single units or clusters play a crucial role in space operations.So far,thousands of satellites have been launched into orbit.Recently,the large-scale satellite swarm coordinated flight(SSCF) concept has rapidly become a research hotspot for SUSs due to its good reconfigurability,redundancy,reliability and disturbance resistance.And its remarkable features such as high flexibility,short R&D cycle,and low operation cost have also deeply attracted many researchers [1].Although existing space programs have successfully integrated theory and practice,the different phases of SSCF deployment have placed higher demands on the performance and accuracy of the system in order to fit the requirements of the times,which leads to extensive research on the corresponding control techniques.
Linear systems theory has been successfully applied to solve a variety of relatively simple system stability problems[2],and SSCF-oriented linear controllers have been naturally incorporated into research in the aerospace field.Most SSCF systems utilize a linearized modeling process to overcome the inherent difficulties of control implementation posed by sophisticated nonlinear orbital dynamics.This simplification led to the well-known Clohessy-Wiltshire (CW) linear equations for the elaboration of the relative position of SSCF[3].The CW equation,which is one of the most famous models,has built the foundation of various linear control techniques for SSCF systems [4].Considering the engineering needs of SSCF,it seems that there is still a great potential for exploring the integration between nonlinear models and advanced systems theory compared to linear control.Wonget al.[5] proposed a nonlinear adaptive controller based on the integrated nonlinear SSCF dynamics obtained by the Euler-Lagrangian (EL) method and proved the asymptotic convergence of the position tracking error of the leader follower distribution.Since the 1990s,backstep ping [6] has become one of the most popular design ideologies and has been applied to practice for a number of complicated systems.Advantages of backstep ping could be summarized that: i)excellent stability can be achieved with ease; ii) systematic transient performance can be explicitly guaranteed and analyzed; iii) great flexibility of hierarchical controller design for subsystems can be made the best in line with various requirements.Numerous backstep ping design ideas for multiple-input/multiple-output (MIMO) nonlinear systems are rationally extended to SUSs.A backstepping adaptive controller utilizing the radial basis function was presented for a two-body tethered satellite system with additive stochastic noise [7],and the backstepping was also employed in the realm of underactuated nanosatellite swarm for attitude position control [8].
System uncertainties caused by unknown parameters,external disturbances,and unmodeled dynamics are ubiquitous in real system operations,and SSCF is no exception.Adaptive control is one of the most typical methods coping with uncertainty to improve system performance [9],[10].In 1988 [11],researchers proposed a concept of “linear parametrization” to linearly parameterize a class of nonlinear systems,where an appropriately selected parameter vector linearly relative to system dynamics could be more conducive to the design of adaptive laws.Many existing adaptive control methods for linear parametrized SSCF systems were directly driven by the certainty-equivalent (CE) principle [12],[13] in order to mitigate the influence of uncertainties.Unfortunately,although CE-based adaptation has been well studied,its inherent drawbacks in terms of robustness and convergence have received little attention,and even elucidating its physical significance is difficult.Therefore,the above viewpoints confirm the fact that adaptive controllers constructed on the basis of CE principles can hardly ensure the accurate implementation of SSCF tasks in complex environments.As an alternative,aσ-modification adaption proposed by Ioannou and Kokotovic [14] fixed the insufficient-robustness issue in the sense.With the help of theσ-modification and neural network (NN) technique,Yinet al.presented an adaptive controller for delay systems with unmodeled dynamics [15].To overcome the presence of actuator faults and saturation,Sunet al.merged theσ-modification adaptive controller into SSCF stabilization problem [16].Nevertheless,better robustness originating from the above ameliorating measure is built upon the sacrifice of system steady-state performance.
Another idea for CE defects avoidance,i.e.,immersion and invariance (I&I),was investigated by Astolfi and Ortega [17].Compared withσ-modification,simply additive robust terms are no longer considered in I&I,while the damping injection for parameter estimation was accomplished by indirect design concepts.Thus,the resulting adaptive law is free from the restriction of term-cancellation,such as CE,and serves as a key factor in constructing attractive manifolds related to estimator errors.However,the innate obstacle of solving partial differential equations (PDEs) originating from I&I greatly increases computational difficulty [18].To surmount this difficulty as well as to maintain the advantages of I&I concurrently,in light of superior tracking performance and low constructing complexity of the low-pass filter (LPF),a novel filter-based I&I control algorithm was proposed for a single satellite by Seo and Akella [19].Further,Lee and Singh[20] extended the filter method into the robust adaptive parameter estimator for the control of the SSCF system.The two methods above filter both systems and reference trajectories,transforming the original tracking problem into the LPF-processed one and thus avoiding the need to solve PDEs directly.However,the costs were the reduction of the system convergence rate and stringent requirement of practical software & hardware.Then,a heuristic technique,i.e.,dynamic scaling,was introduced in research about design of high-gain observer and controller [21],where newly defined state variables were generated by dividing original system states by a scaling factor.Inspired by this,in the research of Karagianniset al.[22],the scaling factor was introduced in I&I technique for the first time to acquire an approximative solution of PDEs,hereafter a high-gain term was used to eliminate deviation caused by approximation.Works for output feedback control for respective classes of SUSs have also been done through scaling I&I adaption [23],[24].Although the combination of I&I and scaling techniques effectively reduces the solution difficulty,few literature deals with high-performance adaptive design for SSCF subject to state constraints and input faults.
Due to the huge number of satellites in the SSCF system and the limited maneuvering space of each member,another focus of control technology should be placed on the security assurance and boundary setting issues to effectively avoid accidents.By replacing the traditional quadratic Lyapunov function (QLF) with the barrier Lyapunov function (BLF),a logarithmic structure built upon tracking error signals during the stability verification was developed [25].The BLF has a feature that its function value tends to infinity as the independent variable approaches a certain value,which in turn derives a control signal that can rapidly suppress the trend of the system error as it approaches a predetermined boundary,thus satisfying the constraint.Renet al.[26] ensured boundedness of a class of MIMO nonlinear system through output feedback backstepping by virtue of BLF and NN approximation.Liet al.[27] ameliorated the BLF frame and proposed a backstepping-based NN controller for a class of delayed systems subject to time-varying full-state constraints.More related researches for state-constrained SUSs based on BLF can be found in [28],[29].Papers above demonstrated the potential benefit of BLF in dealing with full-state constraints for SSCF systems.However,control schemes of the SSCF described above are designed for the fault-free case,i.e.,they do not take into account the possibility of input failures and efficiency losses occurring.
The main purpose of fault-tolerant controller (FTC) is that it can guarantee desirable stability and dynamic properties for specific systems in the event of actuator offset/failure [30].Based on fuzzy logic,Bounemeuret al.proposed a backstepping adaptive controller for quadrotor dynamics,considering actuators and sensors in the presence of multiple faults; in addition,they also provided a Nussbaum gain adaptive fuzzy controller for an SISO system with unknown input direction[31],[32].Another fuzzyσ-modification adaptive FTC was developed for a class of strict-feedback nonlinear system with constant efficiency-loss to achieve semi-global boundedness of all signals [33].Correspondingly to the research field of SSCF,an adaptive FTC was proposed by incorporating the prescribed performance control into the dynamic surface design,which is thereby not only overcome time-varying inertial uncertainty but also able to achieve bounded stability[34].Nevertheless,most of the studies on adaptive FTC schemes do not emphasize on facilitating the system to improve its ability to handle input faults by enhancing the dynamic properties of the adaptive mechanism itself.
Motivated by the preceding discussions,this paper investigates a non-CE full-state constrained adaptive control for a class of SSCF systems subject to input faults.An easily solvable BLF-based dynamic-scaling adaptive (BLF-DSA)controller is proposed such that all the system states will be restrained and the para meteric estimation error will converge to an expectant invariant manifold.The main contributions of this work can be summarized in three points:
1) A novel BLF-DSA control scheme is developed to achieve asymptotic tracking of SSCF systems subject to both input faults and system uncertainties without violating predetermined full-state constraints.The resulting closed-loop system shows better dynamic boundedness and steady-state convergence compared with [5],[8]–[10].
2) The proposed non-CE adaptive controller provides robust asymptotic convergence for all tracking and parameter estimation errors of the closed-loop system.In addition,the error convergence rate of the systematic dynamic process is faster and more flexibly adjustable than those of [15],[16],[28],[29].
3) The results show that the proposed method not only enables the SSCF system to automatically offset sudden actuator failures,but also accurately ensures that the relative positions/velocities before and after the malfunction are always kept within the preset constraints for bounded flight.
The rest of the paper is organized as follows.Section II introduces the control problem formulation and some preliminaries.The design process and the main results for the control law are given in Section III.Simulation examples are provided in Section IV to compare and demonstrate the effectiveness of the proposed method.Finally,some conclusions are drawn in Section V.
II.PROBLEM FORMULATION
The relative position dynamics equation of SSCF is used to describe the relative motion of each link of adjacent satellites in orbit.For convenience without loss of generality,some specific satellites are generally called Leaders and the other satellites around them are named Followers.In this paper,the SSCF system consists of several groups of sub-swarms that track a virtual-Leader satellite orbiting in a desired elliptical orbit,where each sub-swarm is constituted by a central subleader spacecraft surrounded by a series of Follower satellites.
The inertial coordinate system {O,X,Y,Z} is attached to the mass centre of the Earth,and the local-vertical-localhorizontal (LVLH) coordinate of the SSCF system is defined as {Ol,x,y,z},which aims to consistently describe the satellite swarm relative motion via an EL-like form.The diagram of one of the typical sub-swarms refers to Fig.1.In terms of the LVLH coordinate,Olis located at the mass center of the onorbit virtual-Leader centroid; they-axis directs outward along the radial direction fromO; thez-axis is perpendicular to the orbital plane of the virtual-Leader and points to the direction of orbital angular momentum; thex-axis is perpendicular to the other two axes and completes the right-handed rectangular coordinate system.Further,ρi∈R3,i=0,...,ndenotes the relative position vector between two adjacent spacecrafts in the link.
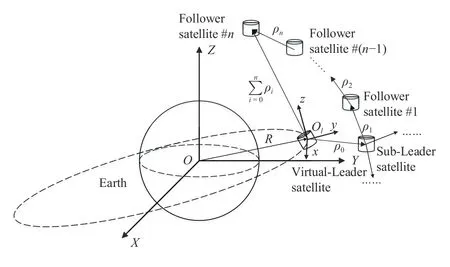
Fig.1.Sketch of Leader-Follower distributed SSCF system in the LVLH coordinate.
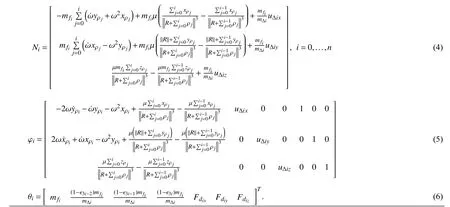
Dynamics modeling of the SSCF task relative to the earth takes advantage of the fact that the systematic energy of satellite motion affected by the universal gravitation is conserved [5].Considering the given link and topology of each sub-swarm in this paper,the overall nonlinear position dynamics from the sub-Leader to then-th Follower based on the LVLH coordinate can be obtained in the following form:


where Σ ∈Rl×lis a diagonal matrix.It is not difficult to obtain Σ=Il+diag(ϵ1,ϵ2,...,ϵl)=I+ΔEwith ϵiemerging on the diagonal elements bounded as -1 ≤ϵi≤0.To expand the SSCF system information in more detail,we propose some general assumptions as follows:
Assumption 1:The measurements of the relative positionqand velocityare all available.
Remark 1:Assumption 1 is a sufficient condition for implementation of full-state constraints and is reasonable.In current spacecraft engineering,the relative position/velocity information could be usually acquired from GPS navigation,line-of-sight (LOS) measurement or spaceborne radar.Thus,state-feedback controllers have been widely employed in SSCF systems [35]–[37].
Assumption 2:The reference trajectory vectoryd(t)∈Rlis smooth and its time derivatives are known and continuous all the time.Meanwhile,thei-th component ofyd,,andare all bounded by known positive constantsky1,ky2,andky3,i.e.,.
The differential equation of the SSCF dynamics has the following property,which will be fully used in subsequent adaptive control method design.That is,(1) actually is obtained by combinating relative orbital dynamics equations of all satellites deployed in order.Thus,premeditating the possible occurrence of efficiency-loss,the nonlinear system model of the (i+1) -th (i=0,...,n) satellite related to the previous one produces an affine parameterization as follows:

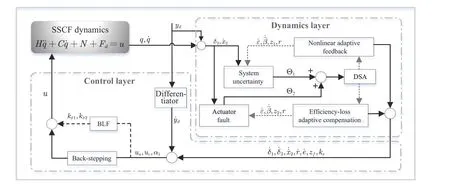
Fig.2.Schematic diagram of the closed-loop SSCF system design flow.
Remark 2:Different values of efficiency-loss factors have different practical meanings.ϵi=0 indicates a healthy actuator,ϵi=-1 means a total failure of corresponding actuator,and -1 <ϵi<0 represents partial efficiency-loss of thei-th actuator.Besides,when actuators of the SSCF system area bsolutely healthy(i.e.,ΔE=0),the second subsy stem of(10)will degradeinto+Bu,and dimensions of the φiand θiare going to be shrunk to (11) (show at the bottom of the page).
III.MAIN RESULTS
In this section,a BLF-DSA controller is proposed for the aforementioned SSCF system through backstepping.The control system structure will be illustrated in Section III-A,and the design process of the adaptive tracking control law is about to be investigated in Section III-B.Furthermore,the stability proof and analysis of the proposed control method will be completed in Section III-C.
A.Control Structure Introduction
Control issue for the canonical form of the SSCF system can be properly divided into a dynamics layer and a control layer.In the dynamics layer,system uncertainties and input faults are compensated via a non-CE adaptive scheme synchronously.Then,in the control layer,the actual control input is required to drive the whole second-order subsystem to approach the virtual control signal simultaneously.
Conceiving of the controller deriving from backstepping technique can be divided into two steps.In the first step,a desired virtual signal built upon BLF is obtained to achieve the tracking issue.Then,considering the possibly sudden appearance of actuator efficiency-loss,the actual control input of the SSCF system could also be regarded into two parts.Wherein,one of them aims to overcome the difficulty of sudden efficiency-loss,and the other is going to compensate the system uncertainties and induce systematic performance to meet desired requirements through an appropriate adaptive law.The structure chart of the closed-loop system is shown in Fig.2.
B.BLF-DSA Controller Design for SSCF System
Define the tracking error as

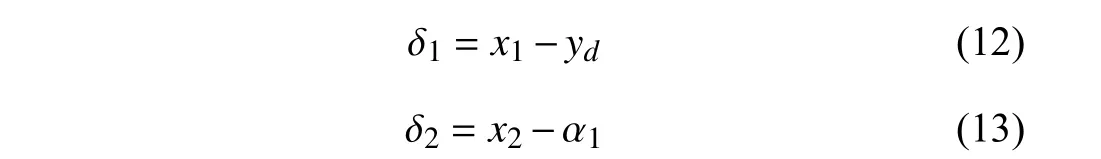
where α1∈Rldenotes the virtual control signal of the firstorder system.To actuate the procedure of backstepping,differentiating both sides of (12) followed by substituting (10)yields to:
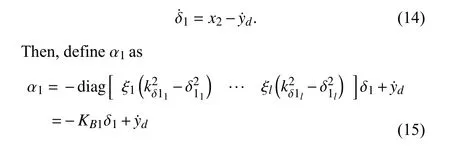
where δ1idenotes thei-th component ofδ1,constants ξi>0,i=1,2,...,larecontrol gains,andkδ1∈Rlisa positive constant vector denoting barriers for tracking error δ1.Employing (15),the δ1-dynamics will be easily arranged as
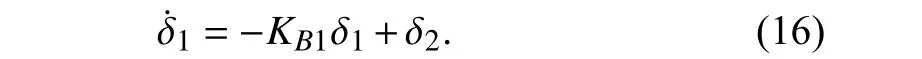
Inspired by the character of BLF to guarantee the constraints of δ1will not violate for all time,one Lyapunov function candidate is proposed as
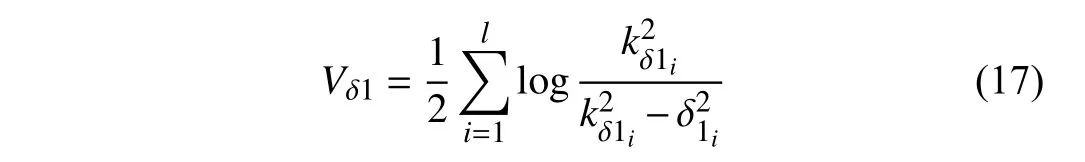

The time derivative of (13) leads to
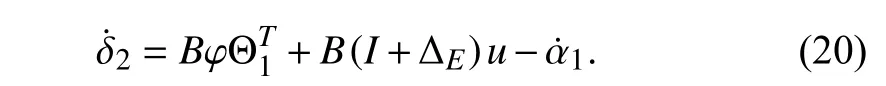
Accident due to the actuator efficiency-loss may occur at any point during the system operation,and certain differences will be reflected in the second subsystem dynamics before and after the emergence of input fault.Therefore,the actual control inputufor the converted SSCF system will be divided into two parts in order to deal with the interference deriving from input fault phenomenon presented in (10) as the efficiency-loss matrix ΔE,that is
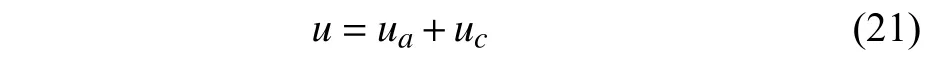
whereuais applied to deal with the input efficiency-loss whileucdenotes the feedback control signal to compensate for nonlinear terms in (20) and stablize the SSCF system.Thus,it is not difficult to obtain
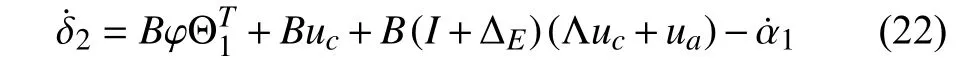
where Λ=(I+ΔE)-1ΔE.According to the above,uncertain termΛucthat cannot bedirectly compensated throughuanecessitates redefining a para meter vector Θ2∈Rlfor mitigating its influence.Need of special note is that,for the unification of adaption design,unknown Λucwill be rearranged into an equivalent form as,i.e.,

where Λiianducidenote thei-th diagonal element of Λ and thei-th element ofuc,respectively.Hence,in the light of the time derivative of (15),the δ2-dynamics can be obtained as
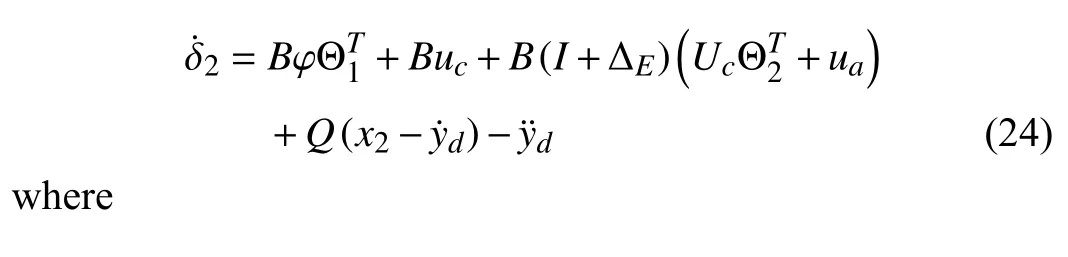
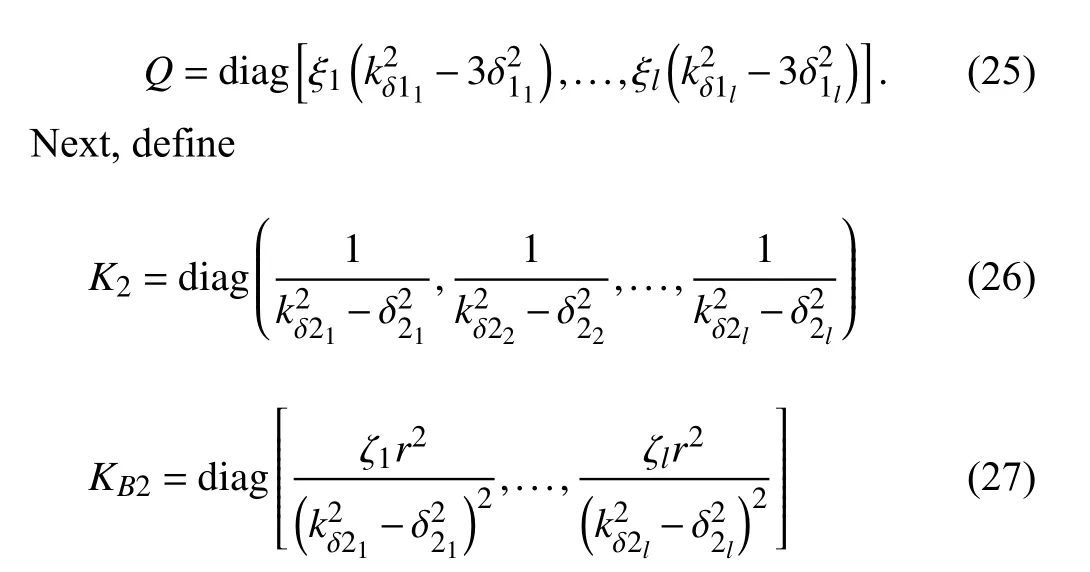
where,similarly,kδ2∈Rlindicates a vector of positive upper bounds for elements of δ2,ζi>0,i=1,2,...,ldenote constant control gains,andris a dynamic scaling factor to be discussed.Therefore,the adaptive compensatoruaand the nonlinear feedbackuccould be organized as
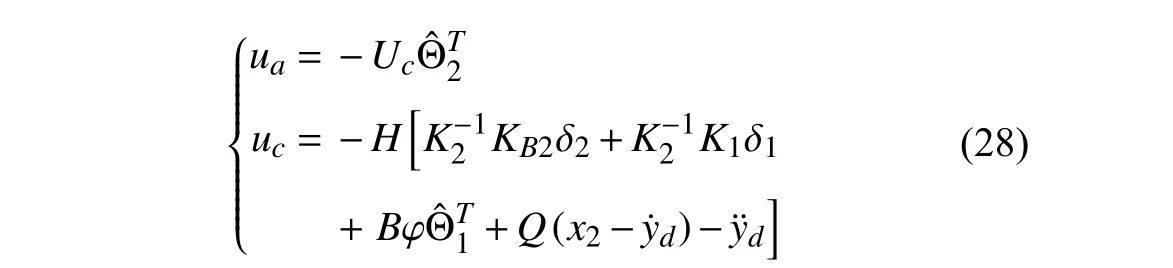
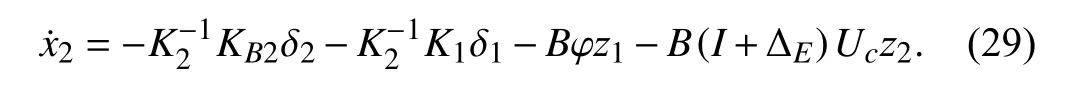
Remark 3:Differenting from the common uncertain nonlinear SSCF systems,the closed-loop dynamics differential equation in (29) contains two groups of parametric estimation errors (i.e.,z1andz2).In addition,unlike common parameter linearization in adaptive control,thez2vector is multiplied by the regression matrixB(I+ΔE)Ucwith an unknown term and a controller-coupling term,instead of a completely known simple matrix.Hence,direct employments of classic CE adaptive mechanisms show their incompetence when tackling the above system,which could be seen in Section IV.

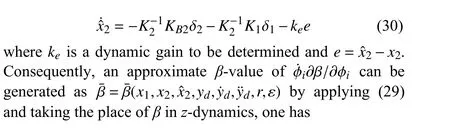

Note that the matrixI+∂β¯/∂ε is invertible since the second term only contributes to non-diagonal elements.After substituting (28) and (29) into (31) and letting the functionbe set as
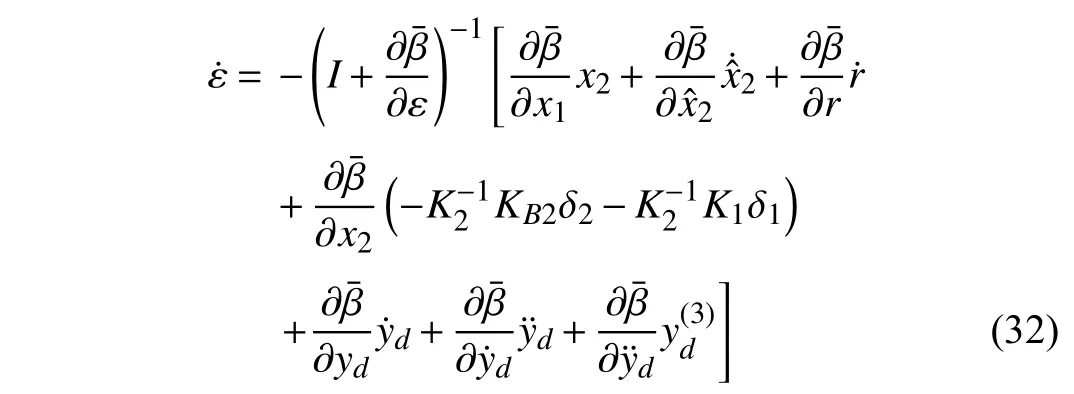
it can be easily obtained that

It should be mentioned that ϑ(Δ),the last term in the above equation,can be regarded as a disturbance in the parameter estimation error dynamics.To handle this undesired disturbance,a scaled parameter estimation error is proposed as

whose time derivative can be obtained as
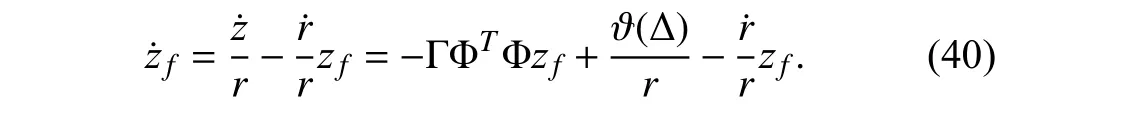
Substituting (39) into (29) yields

while the dynamics ofecould be obtained simultaneously as
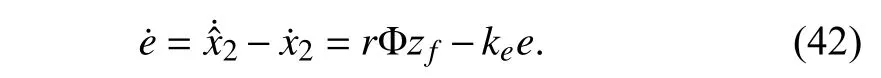
At this point,consider another BLF-like Lyapunov function candidate

Immediately afterward,the proof of the boundedness ofr,the attractiveness and invariance of a specific manifold related to error signals,the asymptotic stability,and state-constrained property of system (10) will be presented in the next subsection.
C.Stability and Boundedness Analysis of Closed-Loop System
Theorem 1:Consider the dynamic equations presented in(10) satisfying Assumptions 1 and 2 and initial conditions(i.e.,δ1(0)∈Ωδ1and δ2(0)∈Ωδ2),the BLF-DSA controller constructed in (21),and the adaptive law in (32) and (35).Further,define ther-dynamics and matrixkeas

1){ There exists an attrac}tive and invariant manifoldS=z∈RL,e∈Rn|Φzf=e=0such that the error system represented by (40),(42) will converge to it asymptotically asrconverges to some finite value>1;
2) The relative position vector q will track yd(t)asymptotically, i.e., l imt→∞δ1(t)=0;
3) Any element of q and of the closed-loop system will not violate the imposed constraints indicated bykq1i kq2i,i=1,...,land for all time.
Proof:To begin with,choose a Lyapunov function candidate as
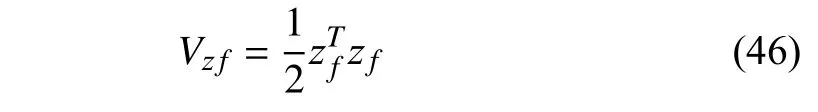
whose time derivative,by right of (40),is expressed as
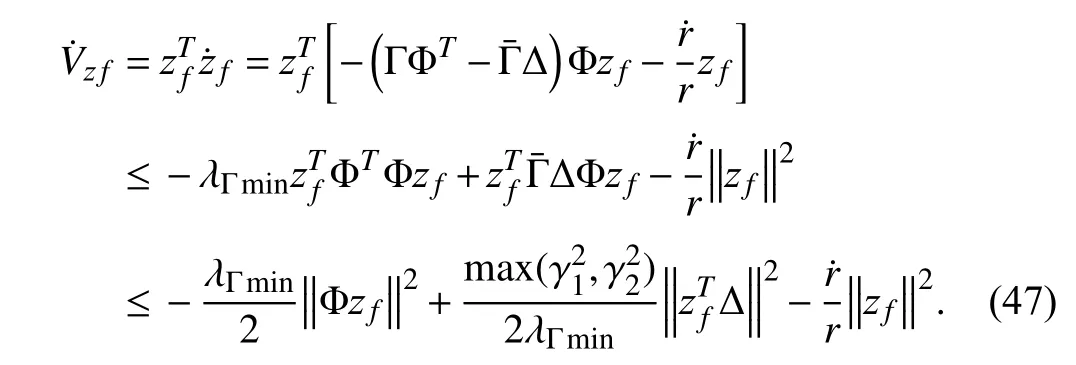
Clearly,from (44),it is not difficult to find out that the scaling factorrincreases monotonously on account of>0,t>0.Substituting (44) into (47) and referring to the matrix norm compatibility lead to
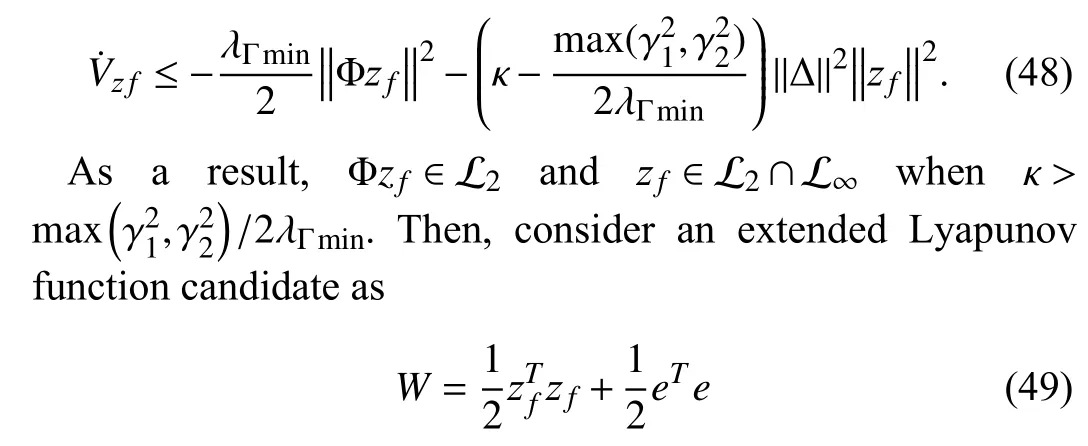
whose time derivative,along (42) and applying (45),can be obtained as
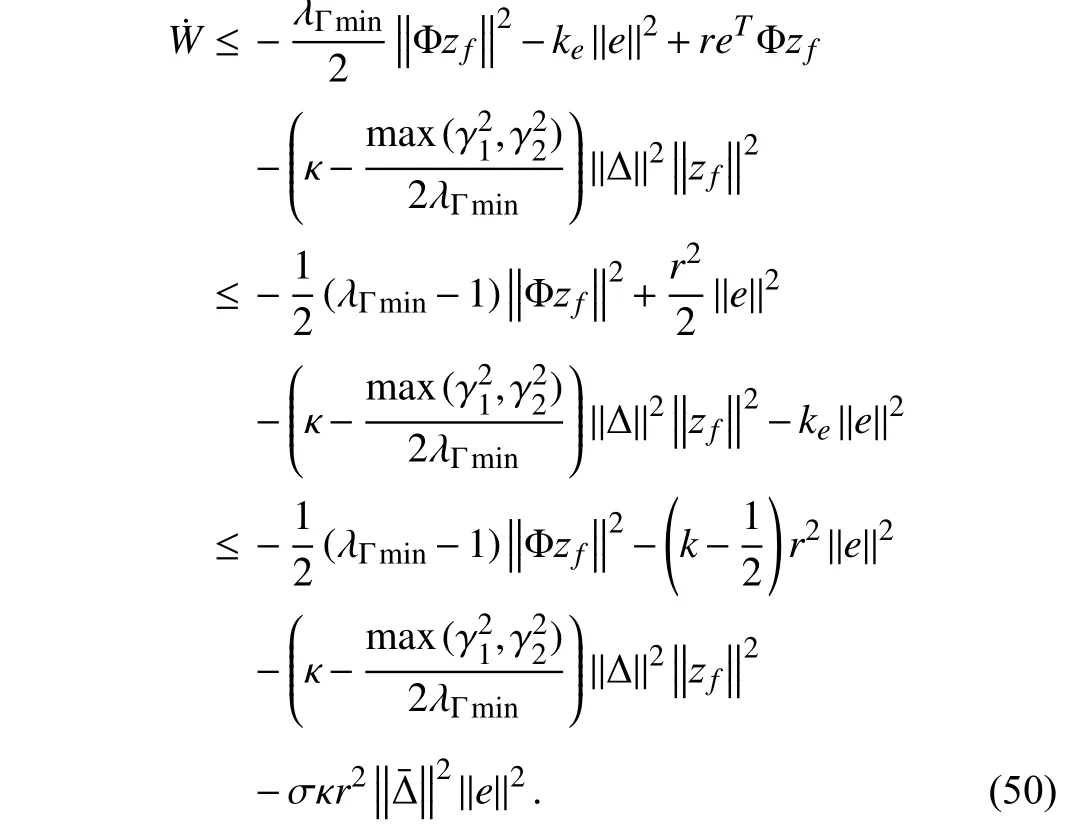
Then,it remains to discuss the boundedness of the scaling factorr.Continue to expand the content of Lyapunov function candidate,select
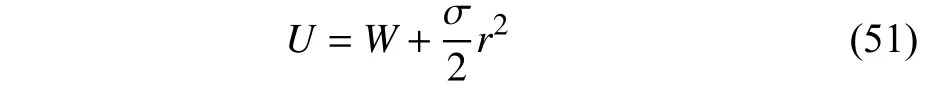
and recall (44),it can be obtained
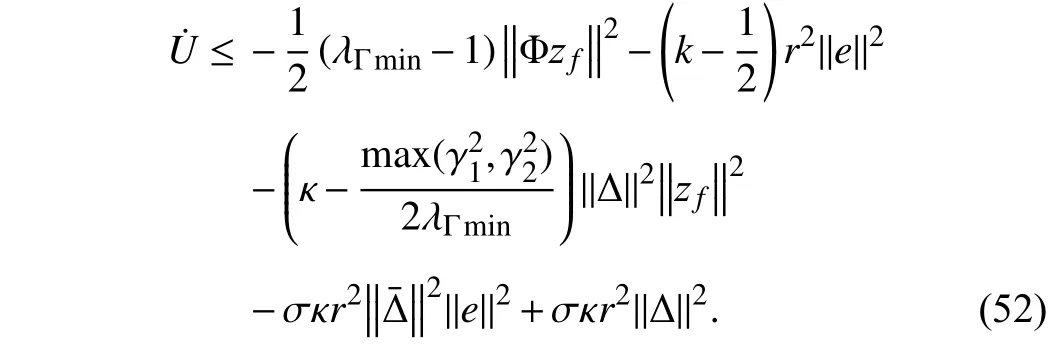
It is important to emphasize that in terms of (37),the last two terms of above inequation will cancel out.Therefore,

Taking the derivative of (43) with respect to time along (24)and substituting into (18),(29),and (30) yield

i.e.,x1(t)→yd(t) ast→∞.This completes the proof of 2).
Finally,sinceVδgiven in (43) is positive definite and referring to (54),there isVδ(t)≤Vδ(0),t>0 while interference of extra termdcould be overcome according to the derivation and analysis process in 2).Now,considering the logarithmic function,the following property holds:

which can be rearranged as
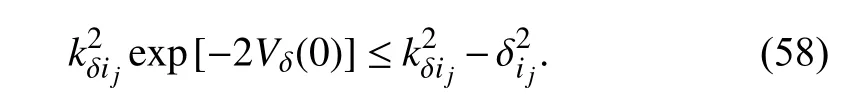
Then,(58) yields

Remark 5:From (52) with properk,κ,γ1,and γ2,it follows that the adaptive process ends up with all signals converging to the manifoldS.The I&I technique will not try to cancel the perturbation terms deriving from the parameter estimation errors,which is the most significant difference from the CEbased adaptive methods.It established an attractive manifold derived from the separate-design ideology to improve the performance of the estimator.Moreover,the attractive property ofScan always ensure asymptotic convergence of the off-the-manifold states under properly designedzdynamics,even in the presence of external disturbances.
Remark 6:Notice the structure ofKB1in (15) andKB2in(27),one can modify the constitution of each element,i.e.,

Remark 7:To ensure the validity of the stability proof of the closed-loop SSCF system,the initial conditions ofx1(0),x2(0),andyd(0) have to be chosen appropriately so as tosatisfyδ1i(0)∈Ωδ1and δ2i(0)∈Ωδ2.Sinceyd(0)is definitely known andξiis prescribed in advance,the maximum value of α1(0) can be computed.Thus,kq1andkq2can be easily obtained.
Remark 8:It can be clearly drawn from the above analysis that on the basis of satisfying asymptotic stability,shrinking γi,i=1,2,...,lcan effectively reduce the available minimum value of κ.Correspondingly,the final value of the scaling factorrand dynamic gainkewill decrease as well for the feasibility of the control implement of SSCF system.The parameterskand σ are employed to adjust the growth rate ofkein order to make the velocity observation trackx2in a reasonable trend.Besides,the gains ξiand ζiwill directly affect the required control inputs and the value of the“approximation error” Δ.Therefore,to ensure feasibility,the necessary trade-offs for control gains must be considered within an acceptable range.
Remark 9:Distinctly from the adaptive laws provided in[5],[9],[16],[29],[33],etc.,the CE-based or sigma modification schemes use a single error-driven parameter estimate to eliminate the effect of uncertainties (i.e.,=θ-),which cannot completely reliably guarantee the system convergence.Thez=ε+β-Θ defined through I&I indirectly injects the damping term/∂x2Φzinto the estimator dynamics,thus improving the overall uncertainty resistance and fault tolerance of the SSCF.In addition,the conventional QLFs are always radially unbounded,while the logarithmic function in the BLF effectively limits the range of variation of its independent variables.
IV.NUMERICAL SIMULATIONS
In this section,the effectiveness and advantages of the proposed BLF-DSA controller for SSCF system are illustrated through numerical simulations.To accomplish a more detailed and profound contrast for unfolding the discussion of this paper,the proposed method,the primal I&I-based QLF one,the typical CE-based BLF one,and the CE-based QLF adaptive method will all be respectively employed in the following testing system with identical initial conditions.

wherealis the semi-major axis of the elliptical orbit,elis the orbital eccentricity,and φ(t)∈R is the time-varying true anomaly of the planar dynamics of the virtual leader target.Besides,additional parameters applied in this simulation task within the dual-satellite system are determined as follows:
At some point during the operation of the system,the mass information of both satellites is assumed to bemf0=mf1=20 kg,[and the efficie]ncy-loss factors are determined as1+sgn(t-100)×diag(-0.3,-0.8,-0.2,-0.7,-0.4,0).In other words,the input fault is going to happen whent=100 s.
All the sequent simulation results of the tracking mission are uniformly built upon the same initial conditions given as

Note that for the feasibility of the proposed BLF-DSA controller,a series of barrier values should be set to satisfy δ1(0)∈(-kδ1,kδ1) and δ2(0)∈(-kδ2,kδ2).Thus,the constant constraints of the states and gains of the BLF-DSA controller in order to obtain good tracking performance for the dualsatellite system are selected as follows (the trade-off among parameters can refer to analysis in Remark 7):
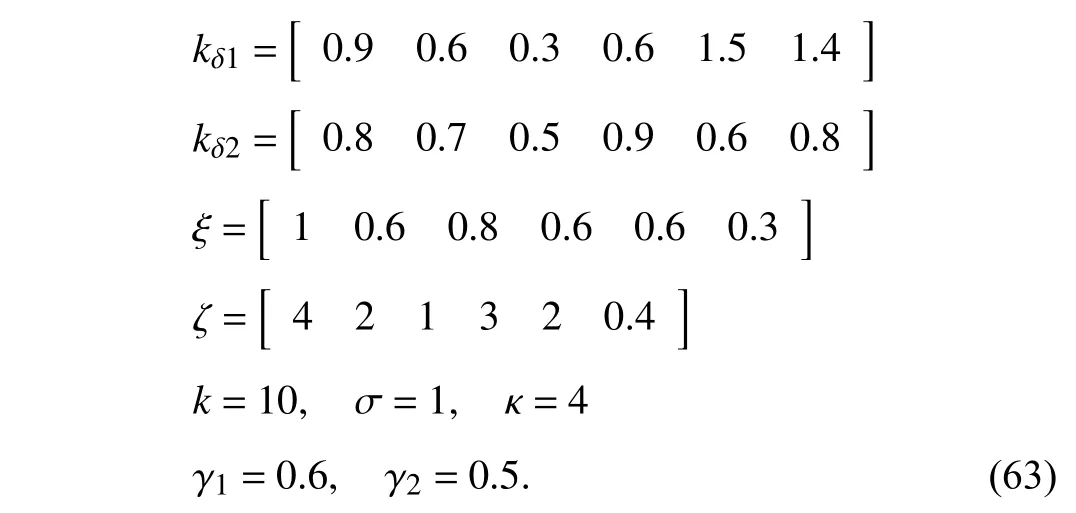

Finally,the desired motion trajectories are selected as the inequality relationship shown in (37).In order to save paper space,particular description of this inequality relationship between Δ andwill not be expanded here.
The selection of the preceding desired trajectory did not take into account any fuel consumption considerations;however,it illustrates the capability of the proposed controller to finish the tracking task suffering the occurrence of input fault and external disturbance.Following the design process in the previous section and all of the above assignments,the final control signal for this example SSCF system can be obtained by synthesising (28),(30),(34),(44),and (45).
Firstly,it is paramount to show the effectiveness of the proposed BLF-DSA controller.Diagram of the actual maneuvers of both satellitesalong the desired trajectoriesqd1andqd2is displayed in Fig.3,in which two satellites approach the virtual center from their initial positions and encircle on different elliptical orbits.
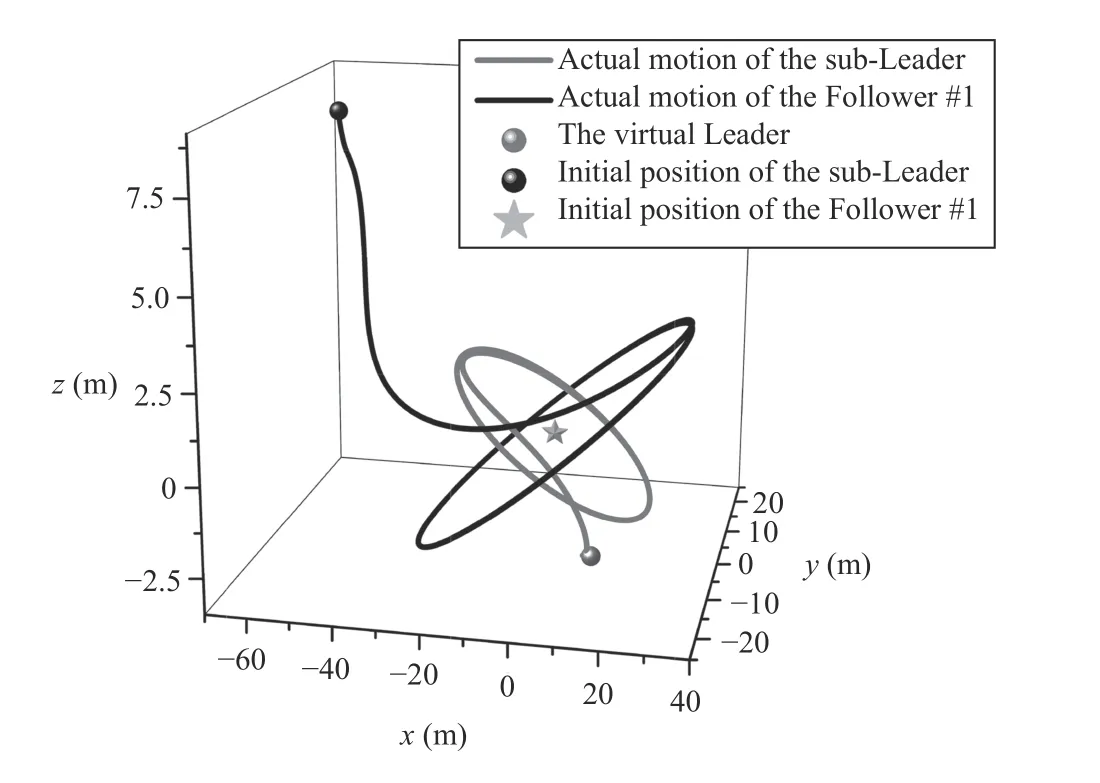
Fig.3.Simulation schematic of the dual-satellite trajectory.
To be specific,subfigures of Figs.4 and 5 illustrate that both ofq0andq1couldconvergetoqd1andqd2intwo sets of Cartesian elements of LVLH,respectively.Considering the discrepancy of both relative position and velocity between the actual motion and the desired trajectory,it can be seen
that the proposed controller makesup for thoseinitial errors(i.e.,δ1(0)=[-0.8,0.5,0,-0.5,-1.4,1.2]Tm,δ2(0)=[0.164,-0.179,0.10,0.467,0.056,-0.413]Tm/s)and is up tothe anticipant tracking performance within 10 s after taking effect.Curves of control forces of the sub-Leader and the Follower#1 are given in Fig.6.Retrospecting (5),the termuΔ1appears in the regression matrix of the Follower #1.Thus,the control input required by the Follower satellite has to additionally overcome the effect caused by the control torque from the sub-Leader,which could be easily observed in Fig.6.
Next,the comparison of images visually reveals the advantages and favorable characteristics of the proposed method compared to the rest of the schemes.Comparisons of δ1,2-images between the proposed BLF-DSA controller and the other three comparable techniques under the same set of initial conditions are shown in Figs.7 and 8,respectively,with different type of curves.In general,methods involved here can be compared based on two benchmarks,one of which is“QLF or BLF” and the other is “CE or non-CE”.Proper parameters are chosen in order to keep all the initial conditions inside the sets Ωδ1and Ωδ2as many as possible.However,from the simulation curves,there are significant differences in the dynamic characteristics of the tracking error curves.
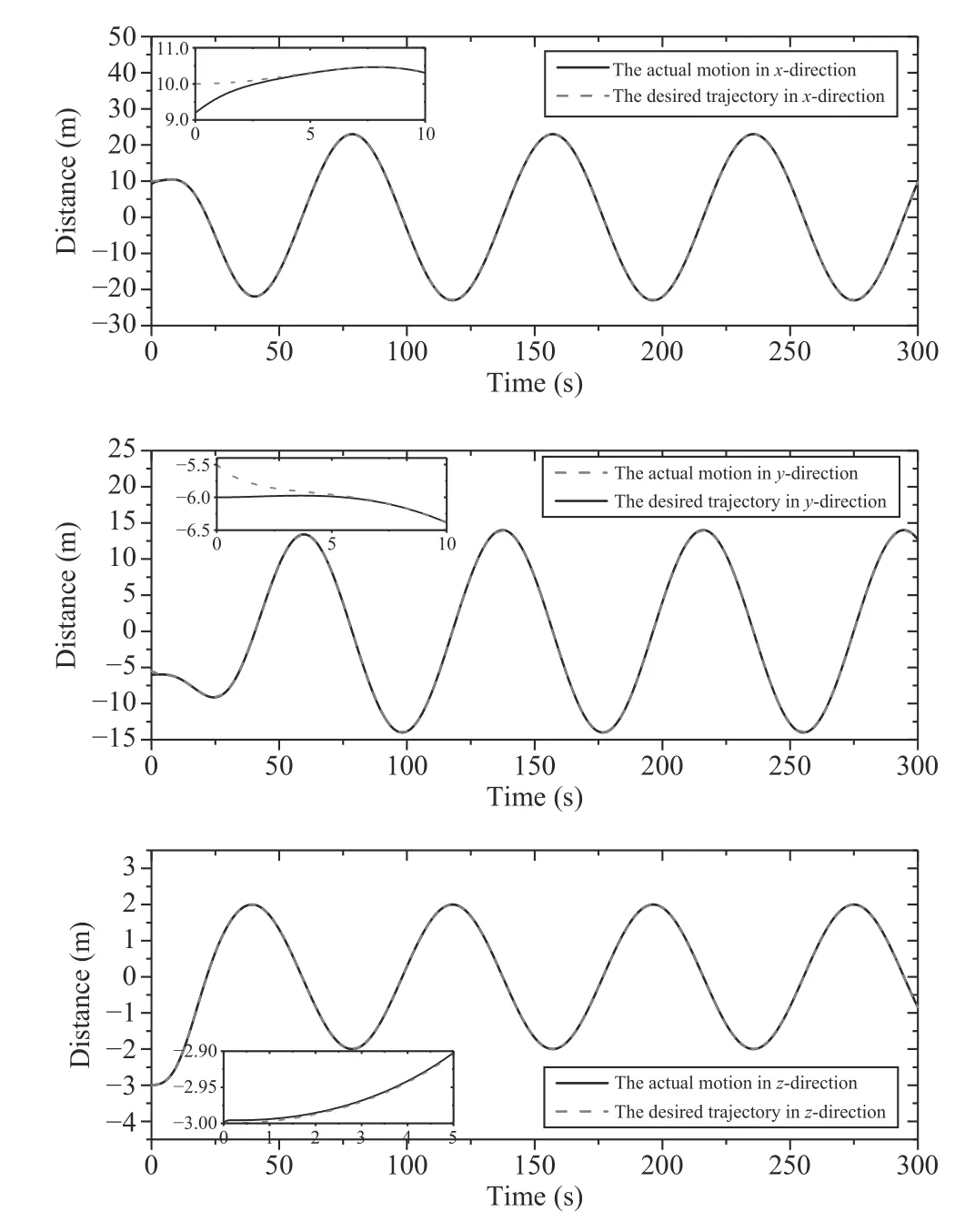
Fig.4.Tracking performance of the sub-Leader satellite in the{x,y,z}direction.
Starting with the former benchmark,in Figs.7 and 8,it is clear that oscillations of QLF-related curves are much more pronounced than that related to BLF as a whole.The upper middle,upper-right,and left-bottom subfigures of Fig.7 particularly emphasize the fundamental differences between QLF and BLF frameworks in the performance of relative position tracking boundedness,in which both of the QLF controllers exceed the predetermined error constraints while those of BLF avoid boundaries violation (i.e.,δ1i≤kδ1i).Similarly,Fig.8 shows the excellent property of prescribed boundednessofδ2brought by theBLF(i.e.,δ2i≤kδ2i).As has been expoundedin Theorem 1 and Assumption 2,sincecan be computed and the upper bounds ofqdandq˙dare certainly known in advance,referring to the favourable characteristic of BLF,it can be concluded that both ofx1andx2are respectivelyc(onstraine)d wi(thin two)corresponding open intervals,i.e.,-kq1,kq1and-kq2,kq2.
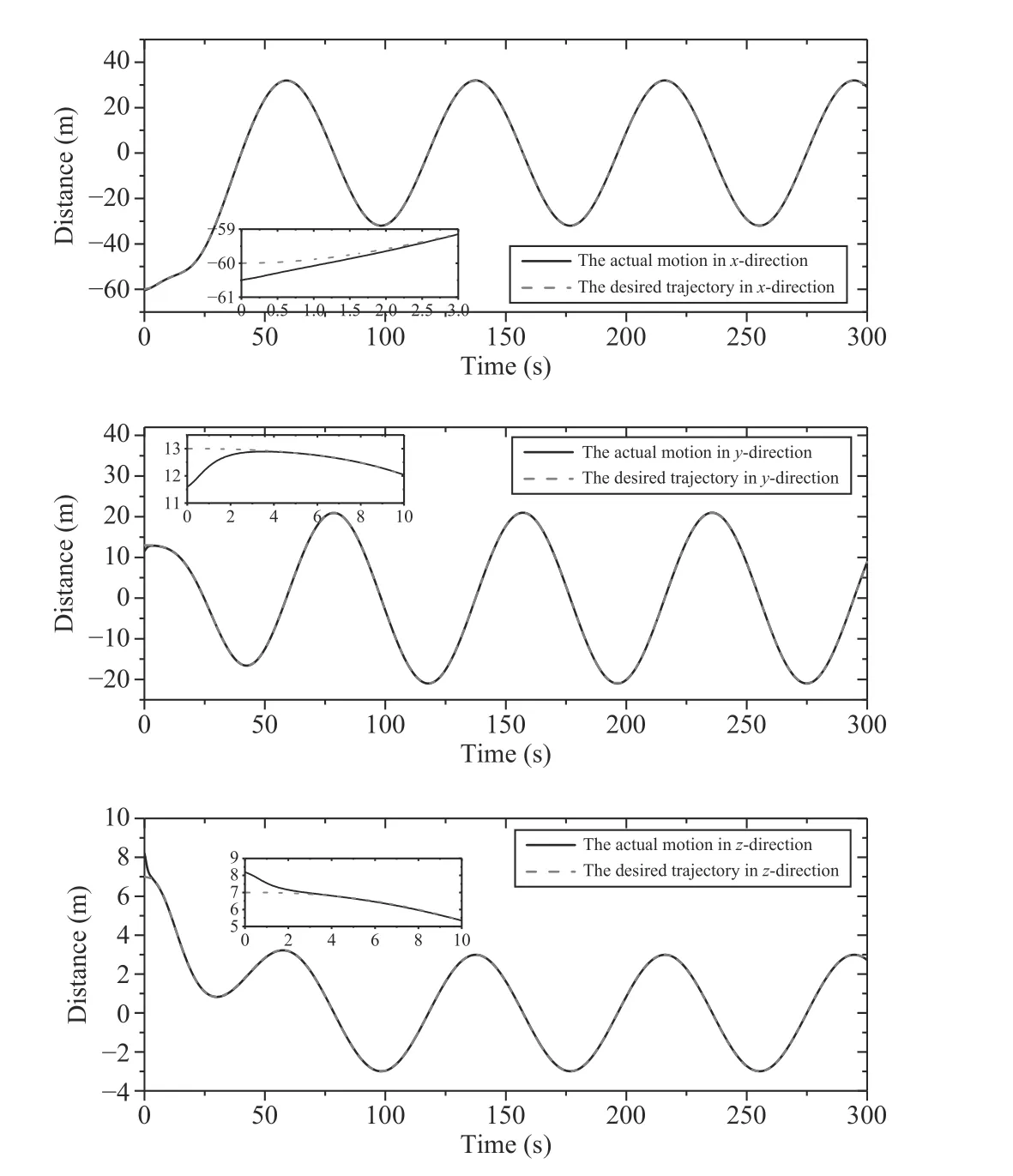
Fig.5.Tracking performance of the Follower satellite #1 in the{x,y,z}direction.
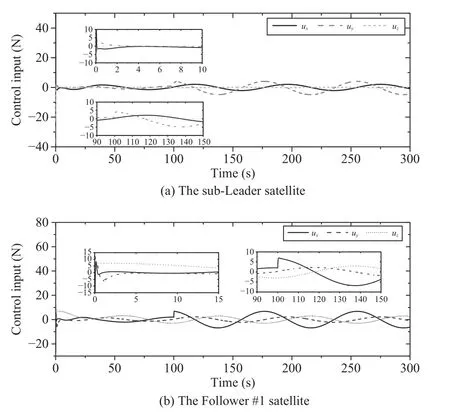
Fig.6.Curves of control inputs of the dual-satellite system in { x,y,z}.
It is worth noting that the tracking error performance obtained by the proposed BLF-DSA controller clearly has better steady-state characteristics than other methods,regardless of whether input efficiency losses occur or not.This advantage is mainly attributed to the excellent performance due to the damping injection in the I&I technique and the flexible application of the scaling factor.However,taking both the initial tracking errors should be restrained within Ωδ1∩Ωδ2and the extreme complexity of establishing a properβafter the efficiency-loss into account,control gains and adaption of the primal I&I-based QLF controller have to be selected quite conservative which yields worse performance (i.e.,the short dash lines).Relatively small control gains required by the QLF methods ensure that the system states do not exceed constraints as much as possible at the beginning,but greatly reduce the overall convergence of the system.That is,the system might oscillate sharply or present large-amplitude overrun.
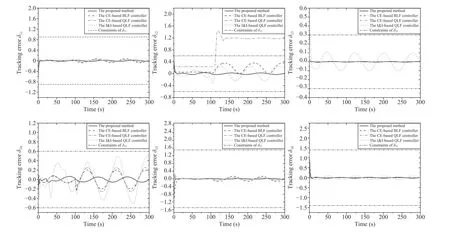
Fig.7.Image comparisons of tracking errors δ1 between the proposed method and others. The
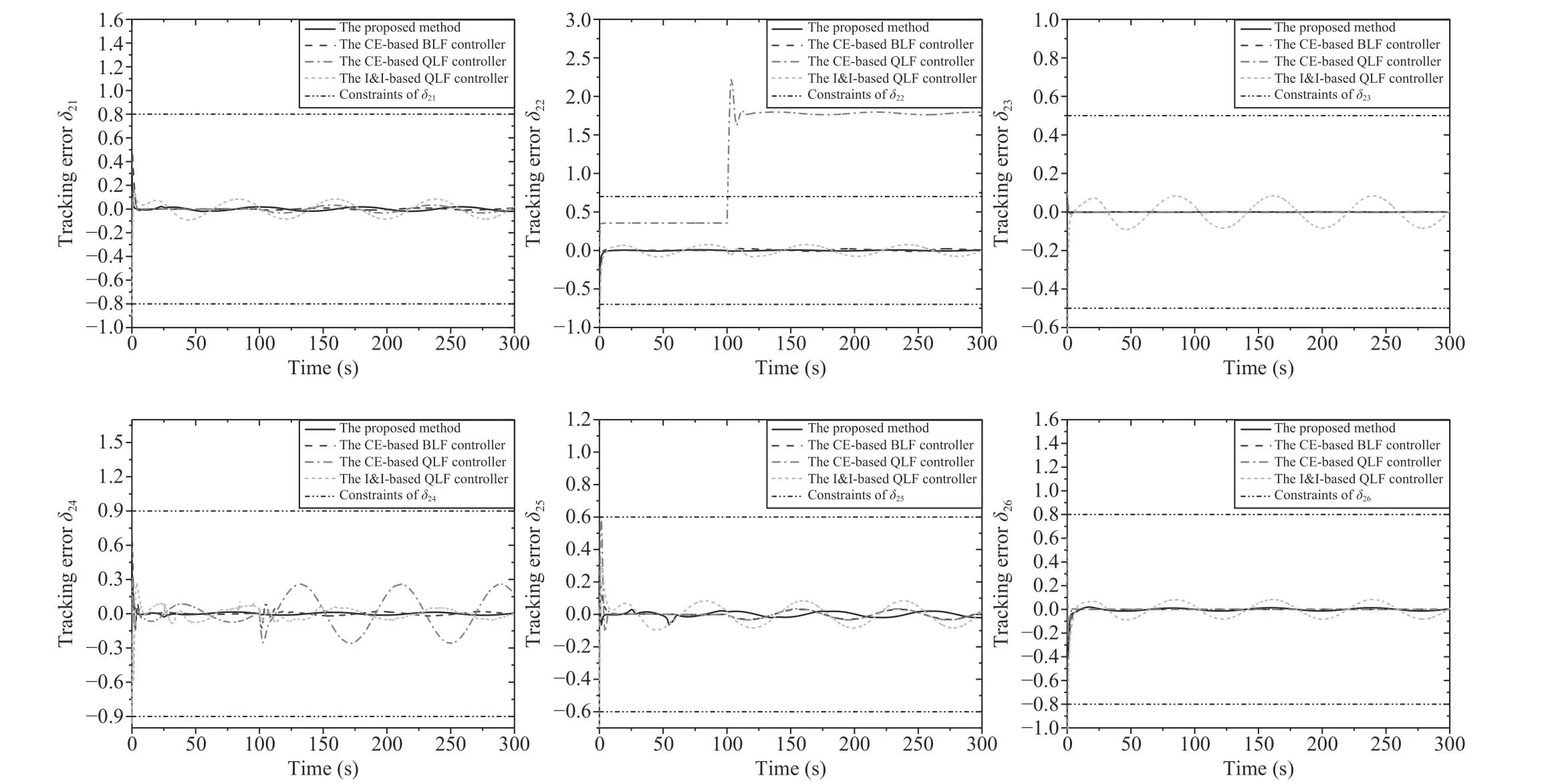
Fig.8.Image comparisons of tracking errors δ2 between the proposed method and others.
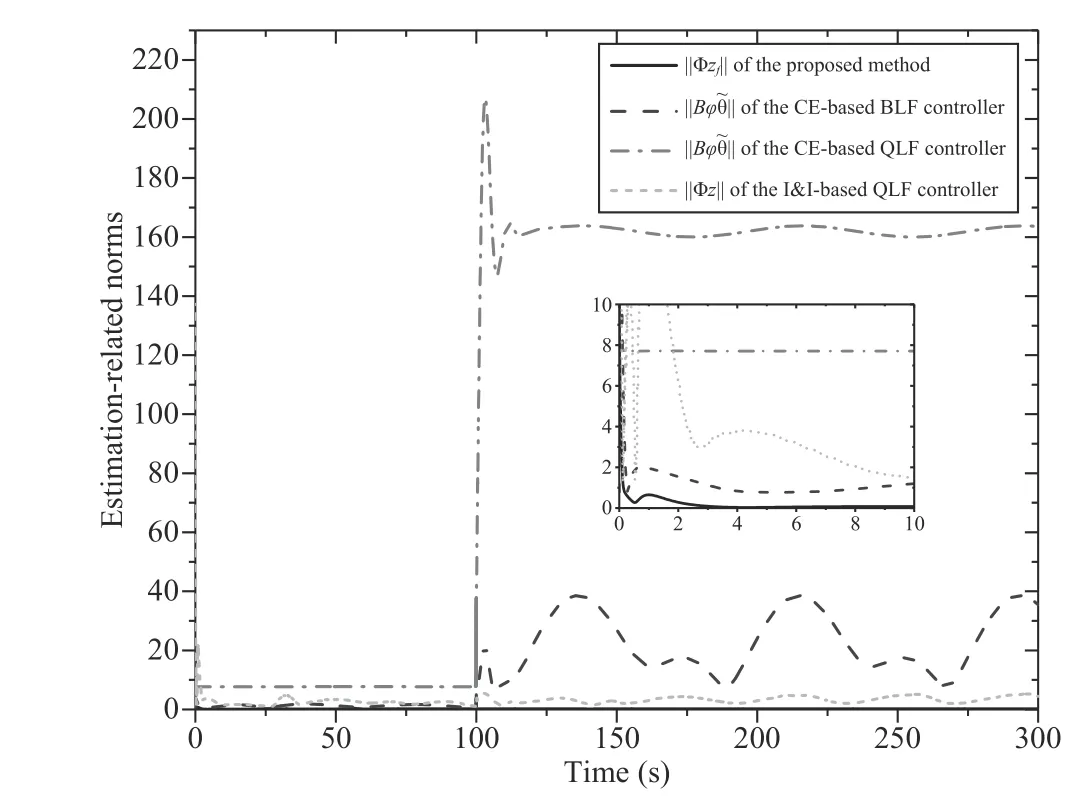
Fig.9.Image comparisons of parameter estimation error between the proposed method and others,where =θ-.
Then,pay attention to the second benchmark,Fig.9 clearly indicates the performance of the respective parameter estimation dynamics of the listed adaptive methods over time.Among them,the norm of error-related manifold of the proposed method converges to the aforementioned attractive and invariance manifoldSwhile that of the other methods show distinguishing performances of non-convergence characteristics.Broadly,curves based on the I&I technique have better convergence than those of CE-based controllers both before and after the efficiency-loss occurrence.It is the powerful evidence that the indirect adaption design ideology circumvents the simple cancellation of the CE frame and provides better convergence and robustness of estimators.When the input fault happens att=100 s,in Fig.9,both of the CE-based adaptions show significant jumps and oscillations,which may straightway cause the necessary control inputs to be impractical in actual situations.
According to the simulation results and analysis of comparisons above,the proposed BLF-DSA controller in this paper has achieved expectant tracking task.Furthermore,the effectiveness and superiority of the proposed controller are verified which not only keeps the states within the desired ranges but also overcomes the influence of input fault and system uncertainties to get better performance for the SSCF system.
V.CONCLUSION
In this paper,a novel nonlinear BLF-DSA controller is developed for the SSCF system suffering from full-state constraints,system uncertainties,and input efficiency-loss.A significant transformation for the SSCF system into its corresponding canonical form is derived to fit the adaptive control mechanism.By employing the backstepping based I&I throughout the design process,the proposed controller can guarantee the asymptotic tracking of the SSCF system,and all estimated error signals will reach the prescribed attractive and invariant manifold.Further,a dynamic scaling factor is applied to the original I&I to build an approximate solution for the PDEs,thus avoiding the difficulty of solving them directly.Meanwhile,the synthesis of backstepping and BLF framework is exploited to ensure all the closed-loop system states will not transgress the imposed constraints.Finally,the effectiveness and superiority of the proposed methodology have been effectively demonstrated and elaborated through a numerical illustrative example and a contrast control group.Potential improvement directions for this BLF-DSA controller should aim at reducing the dependence of the controller on relative velocity signal measurability and considering the input saturation.Extending the proposed method to more complex mission requirements as a future research goal may include the design of output feedback controllers,as well as reducing the requirement for initial constraints in the BLF framework.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Deep Learning Based Attack Detection for Cyber-Physical System Cybersecurity: A Survey
- Sliding Mode Control in Power Converters and Drives: A Review
- Cyber Security Intrusion Detection for Agriculture 4.0: Machine Learning-Based Solutions,Datasets,and Future Directions
- Barrier-Certified Learning-Enabled Safe Control Design for Systems Operating in Uncertain Environments
- Cubature Kalman Filter Under Minimum Error Entropy With Fiducial Points for INS/GPS Integration
- Conflict-Aware Safe Reinforcement Learning:A Meta-Cognitive Learning Framework
