基于SA-GAELM的短期风电功率组合预测
2022-01-26纪志成
刘 兴, 王 艳, 纪志成
(江南大学教育部物联网技术应用工程中心, 江苏 无锡 214122)
目前, 风电已成为主要新能源之一, 风电并网的发展规模逐渐扩大.由于自然风的风电场输出功率具有波动性、随机性和间歇性等特点,会危及并网后电力系统的稳定性和安全性,因此短期风电功率的预测工作极为重要.目前的预测方法主要有物理法、统计法和学习算法.其中, 物理法建模较复杂且计算要求高[1], 而统计法和学习算法的预测精度不理想.故组合方法的开发利用成为短期风电功率预测研究的热点[2].林凯等[3]设计了基于二维参数改进的粒式搜索者算法,对支持向量机的核函数参数和惩罚因子进行寻优;杨锡运等[4]采用粒子群算法优化的核极限学习机预测风电功率,提高了预测精度及速度; Li等[5]针对传统极限学习机预测精度低、模型不稳定的缺点,提出一种基于差分进化和交叉验证优化方法的核极限学习机; Yan等[6]提出一种基于多对多映射网络以及堆叠降噪编码器(stacked denoising auto encoder, SDAE)的多尺度风力发电预测方法; Zhang等[7]在改进灰色模型的基础上提出一种基于神经网络的组合预测模型,在该模型中加入2个天气数值预测(numerical weather prediction,NWP)输出, 提高了灰色组合模型的预测精度;Wang等[8]采用最大相关准则算法,建立新的执行函数,在此基础上优化反向传播(back propagation,BP)算法,以提高风电功率预测的准确性; Chen等[9]将模拟退火算法与遗传算法结合,优化BP神经网络,以提高双目相机的标定精度; Wan等[10]提出一种新的基于差分凸函数优化的二分搜索算法,并以此构建机会约束极限学习机模型,提高了算法有效性; 田盛华[11]采用模拟退火算法优化极限学习机进行风电机组风速检测与变桨距控制策略研究.在上述研究的基础上, 本文拟采用模拟退火算法以及改进遗传算法优化的极限学习机模型SA-GAELM进行组合预测, 该方法采用新的选择策略对遗传算法进行改进,避免遗传算法中出现早熟现象,以提高预测精度;采用模拟退火算法寻找极限学习机的权值和偏置的最优解,以加强极限学习机的泛化能力,提高预测精度.
1 模型介绍
1.1 SA-GAELM模型
极限学习机ELM是基于前馈神经网络的一类算法, 具有结构简单、学习效率高的特点,在风电功率预测、变压器故障诊断、风机故障诊断等方面极具应用潜力.传统ELM是一种有监督的学习模型,由于训练样本固定,会出现偏离特征数据的缺点,影响预测精度.对此,文献[12]提出一种基于遗传算法的极限学习机(genetic algorithm-extreme learning machine, GA-ELM)预测模型.遗传算法是一种通过模拟自然进化过程搜索最优解的方法, 具有较强的宏观搜索能力和良好的全局优化性能,但在实际操作中易出现早熟现象,导致结果与最优解之间存在误差.对此, 本文在选择算法上加以改进, 不采用传统轮盘赌选择算法,而将种群按个体适应度大小进行排序筛选出新种群, 更好地体现了个体竞争力及优胜劣汰原则, 解决了适应度较高的个体过快占据种群和后期因个体适应度相近而出现种群停止寻优的问题.改进遗传算法思路如下: 1) 初始化种群U; 2) 计算Ui的适应度Qi, 其中i表示种群中的第i个个体; 3) 按适应度从大到小对Qi进行排序; 4) 通过以下策略进行选择:Qi排序处于前1/3, 复制2份个体;Qi排序处于1/3~2/3, 复制1份个体;Qi排序处于2/3之后, 不复制.按照上述步骤将种群进行筛选并重新组合后得到新种群, 该方法可在保持种群基数不变的同时, 缓解遗传算法出现早熟的问题.
ELM的输入层权重和阈值由任意赋值得到, 会导致部分隐藏层神经元在训练过程中无效, 从而弱化极限学习机的泛化能力.故在实际情况中, 须增加隐含层神经元的个数, 神经网络也因此更加复杂.本文采用模拟退火算法对极限学习机进行优化, 再结合改进后的遗传算法, 优化训练网络.
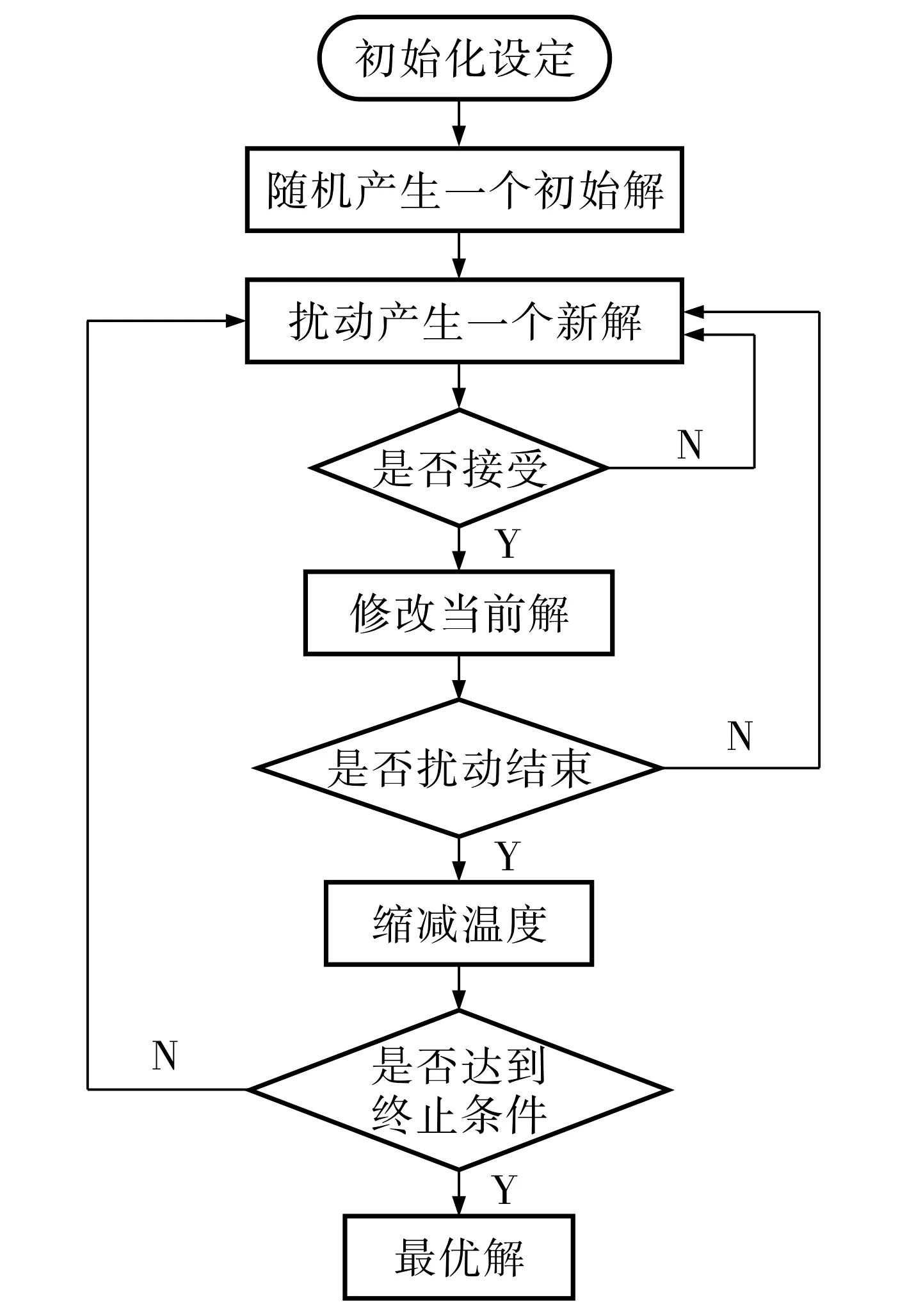
图1 模拟退火算法流程图
模拟退火算法(simulated annealing, SA)是一种基于Monte Carlo迭代求解策略的随机性寻优算法, 该算法模拟固体物质的退火物理过程, 结合概率突跳特性,在解空间中随机寻找目标函数的全局最优解.图1为模拟退火算法流程.第一步, 设定马尔科夫链长度L, 退火初始温度T0, 终止温度Tf和温度衰减系数α, 随机生成一个初始解x0, 并计算相应的目标函数值C.第二步, 扰动产生新解.根据当前解xi进行扰动, 产生一个新解xj, 计算相应的目标函数值E(xj).第三步, 判断新解是否被接受: 若E(xj)优于E(xi), 则接受新解xj; 反之, 若exp[(E(xj)-E(xi))/Ti]大于[0,1)区间的随机数, 其中Ti为当前温度, 则接受新解xj, 若不满足上述条件, 则返回第二步, 直至产生满足条件的新解xj.第四步,当新解确定时, 以新解xj作为当前解.第五步, 循环以上四个步骤, 在温度Ti下, 重复k次扰动和接受过程, 直到设定的迭代次数即马尔科夫链长度为止.第六步, 衰减温度, 当T=Tf时终止算法, 否则继续执行第二步.
改进的预测模型SA-GAELM如图2所示.首先, 采用模拟退火算法对极限学习机的权值和偏置进行寻优, 再用改进后的遗传算法搜索最优惩罚因子,最后使用参数优化后的ELM模型进行功率预测.
1.2 SA-GAELM模型的模糊信息粒化
模糊集理论的应用较为广泛,其核心思想是信息粒化,即分解整体为部分的一种思想,能有效地描述给定数据的输入与输出关系.一般可以用模糊聚类数值观测的方法构建模糊信息粒子.由于点预测无法满足风电功率预测的实际需求,本文采用模糊信息粒化法[12]对数据进行处理, 为风电功率预测提供有效信息.SA-GAELM预测模型如图3所示.首先, 从最大功率点跟踪(maximum power point tracking, MPPT)控制的风力发电系统中提取样本数据, 并进行模糊粒化处理,得到最小值、平均值和最大值数据集; 其次, 将处理后的数据归一化;再次,将归一化后的数据放入SA-GAELM模型中, 预测下一个时序窗口下风电功率的最小值、平均值和最大值; 最后, 对预测结果进行分析.
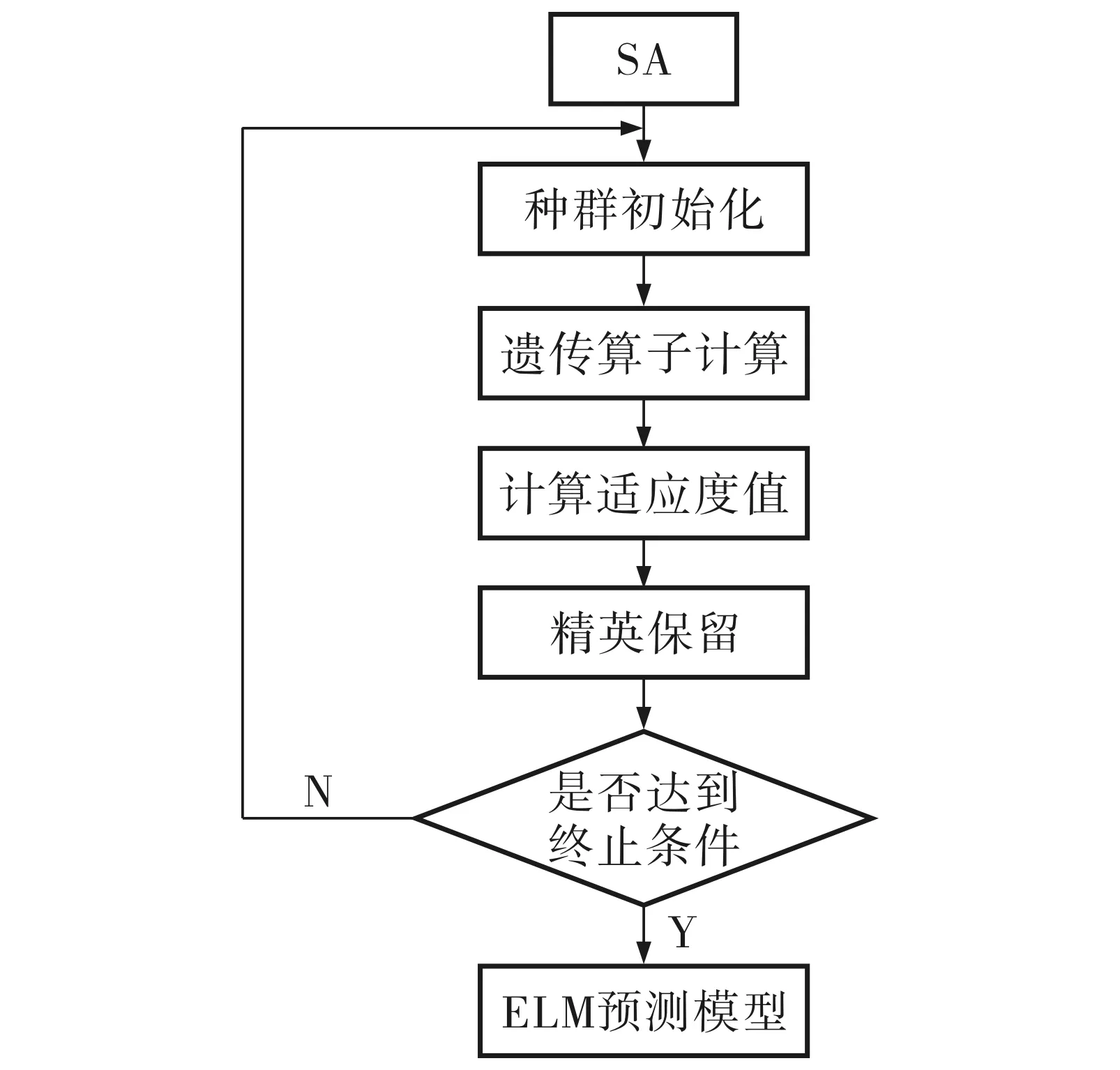
图2 SA-GAELM预测模型
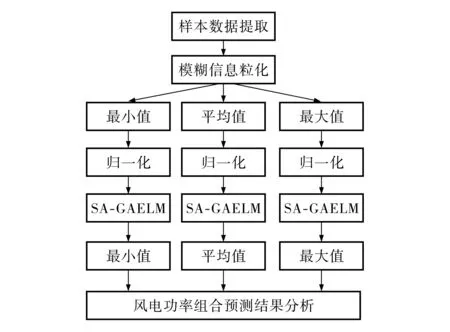
图3 SA-GAELM预测模型的模糊信息粒化
2 仿真与分析
2.1 试验设置
本文采用基于MPPT控制的风电系统进行仿真试验.PI控制中KP-spd=1, KI-spd=4.试验参数如表1所示.通过MPPT风力发电模型, 在2 min内得到13 685组数据, 间隔0.1 s采样、排除无效数据后共保留1 034组数据.试验采用SA-GAELM模型和粒子群算法优化的极限学习机模型PSO-ELM进行预测对比.由于模糊信息粒化最小值、平均值和最大值建模方法相同,本实验以最小值为例建立模型.
根据时间先后顺序, 取前70%组样本数据作为训练集, 其余作为测试集.然后将数据进行归一化, 采用Sigmoid函数作为隐藏层神经元激励函数, 隐藏层节点为60.设模拟退火算法的初始温度700 ℃, 结束温度1 ℃, 每次迭代的温度降幅为5%, 迭代次数500次.设遗传算法进化代数为100代, 交叉和变异的概率分别为0.8和0.1, 种群规模为100.选取测试集的预测输出与期望输出的均方根误差RMSE作为适应度函数, 筛选保留每代中适应度最好的染色体.

表1 试验参数
2.2 仿真结果与分析
以5个采样点为一个窗口对数据样本进行模糊粒化操作,自变量为根据冯卡门频谱所仿真的风速、叶尖速比系数、传动系统的高/低速轴转速、高/低速轴功率、电磁转矩、风能转化系数,因变量为实际输出风电功率.
图4是SA-GAELM和PSO-ELM预测模型下的适应度值进化曲线.从两个模型的各代适应度值平均值的变化趋势可以看出, 采用PSO-ELM模型进行预测, 收敛速度更快, 但在这种情况下易出现早熟现象, 而SA-GAELM预测模型在保证收敛速度的同时, 避免了全局搜索易出现早熟的情况.SA-GAELM预测模型中, 各代最佳适应度值进化曲线在进化20代之后收敛并趋于平稳,各代最佳适应度值平稳下降至最佳值0.005 2, 第100代的适应度平均值为0.005 8; PSO-ELM预测模型中, 各代最佳适应度值进化曲线在第47代之后趋于平稳, 在第100代时最佳适应度值为0.007 3平均适应度值为0.007 5.由此可见, 与PSO-ELM模型相比, SA-GAELM模型在预测过程中的收敛速度适中, 适应度值更高, 预测效果也更好.
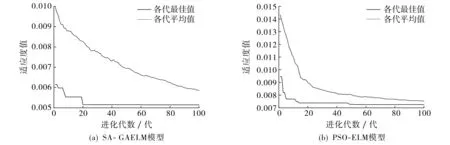
图4 模型适应度值进化曲线
图5是两种预测模型模糊信息粒化最小值测试集的预测误差.由图5可见, 在SA-GAELM模型中,测试集的实际输出与预测输出曲线拟合效果较好, 最大绝对误差约为-42, 而在PSO-ELM预测模型中, 最大绝对误差为60.

图5 模糊信息粒化最小值测试集的预测误差
图6是模糊信息粒化最小值测试集的预测输出与期望输出.由图6可知, 在SA-GAELM模型中,测试集的期望输出与预测输出吻合度较高, 预测效果较好; 而PSO-ELM预测模型中的预测输出与期望输出偏差较大, 预测效果一般.
此外, 本文选择相关系数R2和均方根误差RMSE来量化评价模型的预测性能, SA-GAELM模型的R2=0.999 1, RMSE=44.367; PSO-ELM模型的R2=0.996 5,R2=85.151.可见SA-GAELM预测模型在这两种评价指标下均有较好的表现.
上述试验结果说明, SA-GAELM模型相较于PSO-ELM模型更适用于实际风电功率波动范围的预测, 且模型性能更优, 不足之处在于预测过程中的收敛速度不如PSO-GAELM, 在后续的试验研究中须加以改进.

图6 模糊信息粒化最小值测试集的预测输出与期望输出
3 结论
为有效预测短期风电功率及其波动范围, 本文采用模拟退火算法选择最适的权值和偏置,利用遗传算法的进化能力优化极限学习机的预测能力,并在遗传算法的选择手段上加以改进,弃用轮盘赌法,采用优胜劣汰的选择方法.仿真结果表明, 新的预测模型SA-GAELM具有更好的预测效果,精度更高.
