基于SVMRSAR模型的受教育水平影响因素分析
2022-01-26宗序平
夏 昊, 宗序平
(扬州大学数学科学学院, 江苏 扬州 225002)
21世纪以来, 数据更加多元化, 人们发现单纯的空间自回归模型所建立的回归关系偏差较大, 且适用范围有限,为了解决传统的空间模型的弊端,变系数空间自回归模型由此提出.变系数模型最早在1988年由Shumway[1]提出, 且关于变系数模型的估计方法和假设检验的相关研究已经开展多年.Yatchew[2]系统地阐述了非参数模型的特点, 经过大量数据模拟研究,发现非参数模型的优点在于不依赖于固定函数的假设,具有很强的适应性和实用性; 在此基础之上, Fan等[3]给出了α(·)的两阶段最小二乘估计方法, 并基于局部多项式研究了非参数的最优收敛速度, 证明得到该方法收敛速度的最优性; Pradhan等[4]利用广义似然比检验了具有不同光滑变系数模型的正确性; Fan等[5]提出了半参数变系数模型, 而这一模型类似于线性模型中的混合模型, 既包含了变系数模型中回归系数随指标变量的改变而变化的情景,同时又考虑了回归系数不变的情形,这也是目前处理多解释变量模型至关重要的手段之一.在此启发之下, Sun等[6]创造性地将变系数模型和空间自回归模型结合起来, 构建变系数空间自回归模型, 这类模型可以处理具有空间相关性且波动性较大的数据.经过长时间的发展, Lee等[7]给出了变系数空间自回归模型的参数估计理论, 可以解决潜在的非线性和异质性关系[8], 在单纯的空间自回归模型基础之上,讨论空间数据更深层的含义(空间非平稳性), 具有深刻的现实意义.本文拟以2017年中国31个省级行政区(不含港澳台)为数据样本,利用半参数变系数空间自回归模型对5个影响因素进行可行性分析,探究教育水平发展的影响因素.
1 模型介绍与模拟
半参数空间变系数自回归模型假设为
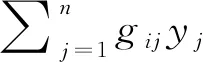
1.1 常数参数的估计
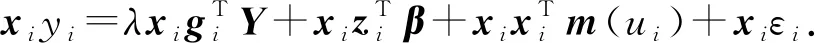
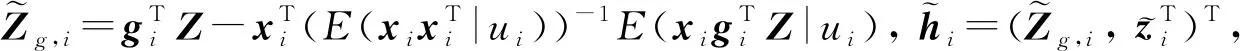
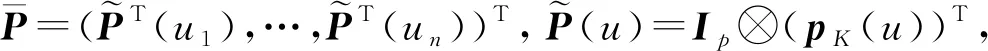
1.2 基于B样条函数序列估计非参数
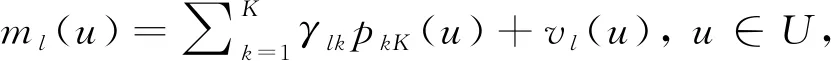
1.3 蒙特卡洛模拟
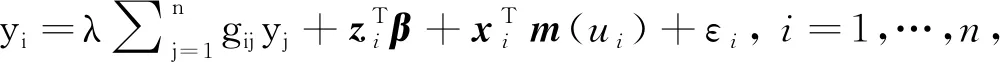
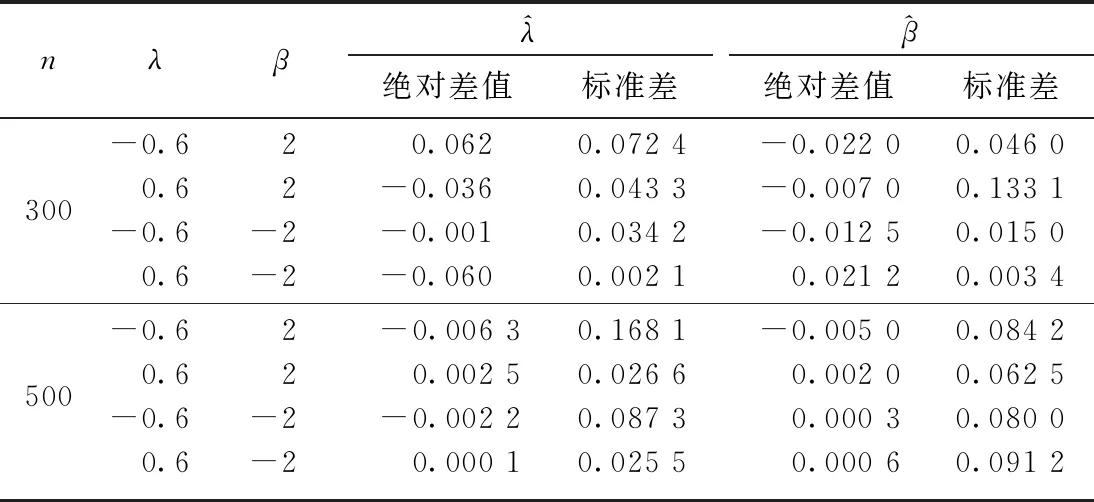
表1 模型的系数估计值
图1为函数m(u)=6[u2+log(1+u)]的图像及λ=0.6,β=2时函数的估计结果.从图1可以看出, 模型的拟合情况良好,而不同常参数下模拟结果类似,拟合结果均较精确.因此,估计的变系数函数很好地恢复了函数的原貌,这也证实了估计方法的有效性和精确性.
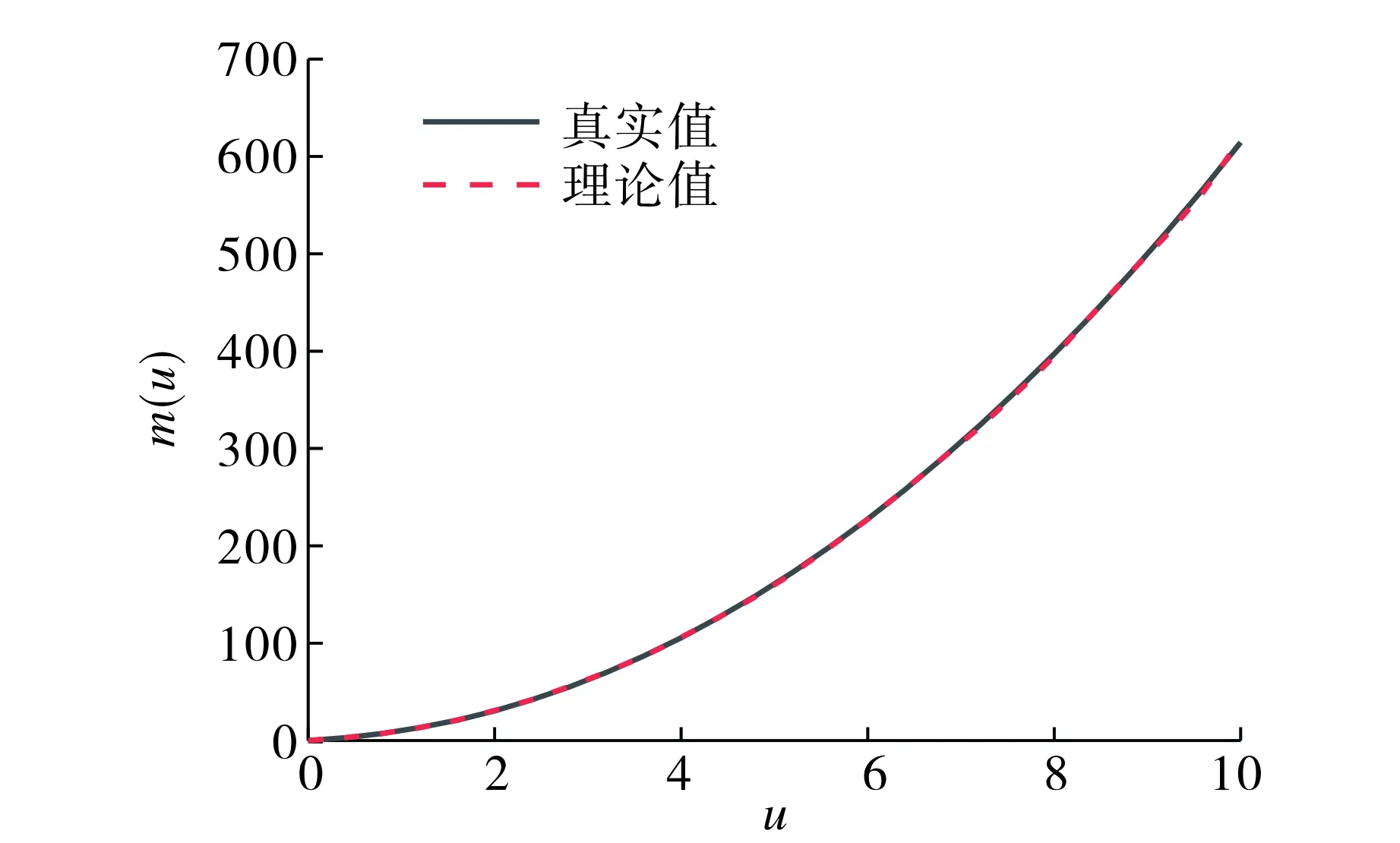
图1 函数m(u)=6[u2+log(1+u)]图像与模拟结果
2 人均受教育年限影响因素实证
人均受教育年限Y是指某一特定年龄段人群P接受正规学历教育年限的综合平均数, 统计公式为Y=E/P, 其中E指各种文化程度的人口乘以相对应的受教育年数之和,P指6周岁及以上的人口总数.本文考虑空间数据可能同时存在两种关系, 利用SVMRSAR模型, 着重分析人口自然增长率p、城乡人口比例u、性别比例s、人均教育投入e、师资配比t等因素对人均受教育年限的影响, 文中所有数据均来自2017年中国统计年鉴.
Moran指数是用来描述空间邻近地区特征值相似程度的统计量, 对于某个区域观测变量Y的全局Moran指数

由表2可知, 人口自然增长率、城乡人口比例、人均教育投入的增加对教育水平的提高都有一定的推动作用,师生比的增加则会制约教育水平的发展,而人均教育投入与师资力量对教育水平发展的影响尤为显著.
由表3可知, 性别比例对教育水平发展的影响具有空间非平稳性.从统计年鉴的数据来看,我国各省男性占比均大于女性占比;从变系数估计来看,男性占比大对人均受教育年限的增长也有正向作用.若影响分为4个等级,其中影响最小的地区有北京、天津、上海等,影响稍强的地区有江苏、浙江等,而性别占比对教育影响较强的地区为新疆、西藏、四川、重庆等,影响最为显著的地区是江西和宁夏等.
图2是31个省市人均受教育年限的观测值和模型预测值(图中各地区代码见表4).图3给出了标准化残差, 图中没有显示一定的趋势性,表明数据具有齐次方差[10].

表2 模型常数参数的估计值

表3 性别比例对人均教育年限的影响
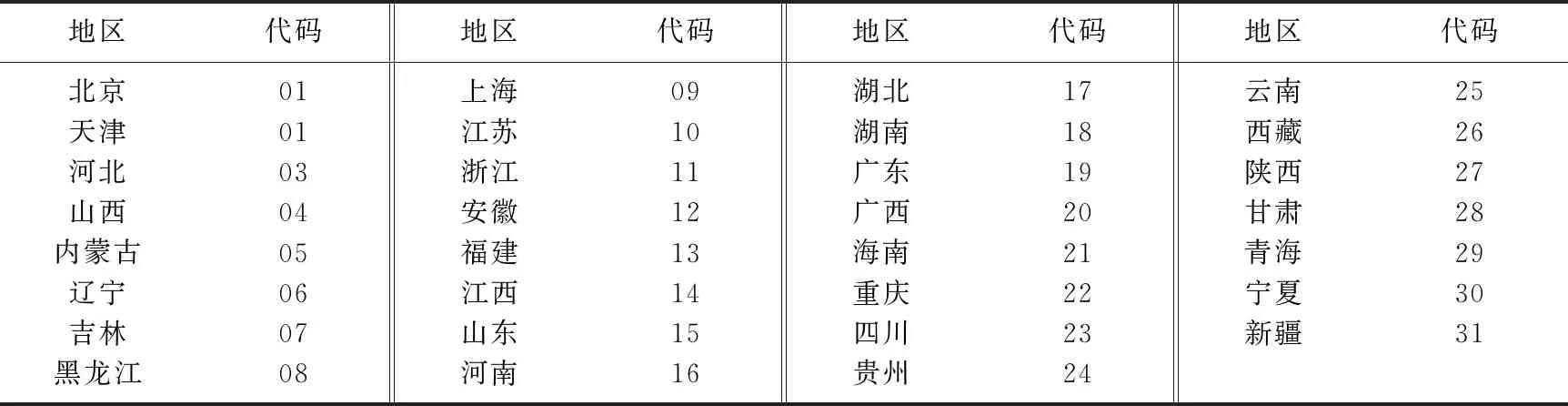
表4 地区代码
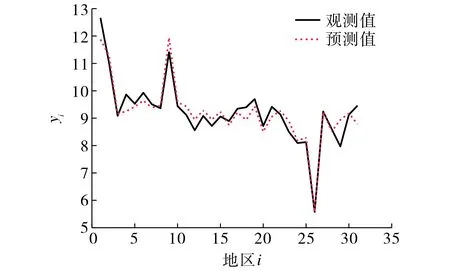
图2 人均受教育年限观测值与预测值

图3 原模型的标准化残差图
