基于排队论和兰彻斯特方程的战时维修保障装备数量确定*

郭一鸣，陈春良，曹艳华，徐玉国，刘 彦

（陆军装甲兵学院，北京 100072）

0 引言

目前，合成部队维修保障装备的战时运用问题未得到有效解决，战时维修保障装备数量规模与作战力量规模较不适应，存在保障装备数量冗余、编配不尽合理等问题。如何使维修保障装备数量规模与作战装备数量规模相适应，是部队装备保障力量运用亟需解决的问题。目前，研究维修保障装备数量确定的方法有很多。陈威、郭齐胜［1］等人针对维修保障装备与维修能力满足度之间的不确定关系，利用模糊回归分析建立线性规划模型，确定了维修保障装备数量；张迁、闫耀东和陈威［2］等人通过维修装备体系仿真，进行维修保障装备数量需求分析，建立了装备维修任务和维修保障装备数量之间的解析关系模型，得出维修保障装备的数量。但这些文献只对平时维修保障装备数量进行了需求确定，所用方法并不适用于确定战时维修保障装备数量。吴同晗［3］等人针对部队维修保障装备数量冗余，利用排队论从伴随保障与定点保障两方面计算了战时维修保障装备数量；钱潜、单志伟、郭红芬、刘福胜［4-5］等人针对保障设备数量配置不合理的问题，建立了基于排队论的装备保障设备数量确定模型，并进行求解。这些文献所用的排队论方法虽然适用于求解战时维修保障装备数量，但是对于排队系统的初始参数装备损伤强度都只是假设，并没有根据某一次具体作战行动、作战装备数量规模进行装备损伤强度计算，所假设数据并不具备说服力。兰彻斯特方程是一种描述兵力动态变化、可运用于作战仿真、模拟参战双方作战装备损耗过程的有效方法，但是传统兰彻斯特方程并不能很好地预测目前信息主导、以快制慢战争的进程和结果，因此，本文对传统兰彻斯特方程引入信息获取及处理系数，建立基于信息因素的兰彻斯特方程对装备受损强度进行计算。

此外，文献［3-5］在确定维修保障装备数量时，均没有考虑不同的待修部位维修时间服从不同的分布，导致计算出的维修保障装备数量不够准确。因此，本文对待修装备的底盘、武器系统、通信以及电子设备加以区分，以某一次合成旅进攻作战行动为研究对象，采用排队论与基于信息因素的兰彻斯特方程相结合的方法，对战时维修保障装备数量进行计算确定，为部队的维修保障力量使用提供理论依据。

1 排队模型构建

在一次合成旅进攻作战行动的维修保障过程中，把待修装备看作排队系统的输入，把维修保障装备看作排队系统的服务机构，为了让待修装备尽可能快地修复并投入到战场中，采用排队先到先服务的规则建立排队模型。战时维修保障主要分为伴随保障和定点保障，其中，伴随保障是战时维修保障最主要也是最实用的保障方式，因此，本文只构建伴随保障的排队模型。

1.1 条件假设

为了简化问题以及建模需要，对模型进行如下假设：

1）在不相重叠的时间区间内装备损坏数量是相互独立的；

2）战场上双方战斗力损失规律用指数分布描述，即排队系统的输入过程是泊松流；在充分小的时间段内，装备损伤的概率与时间无关，且最多可产生1 台损坏装备［6］；

3）在战场损伤中，作战装备机械装置损伤的维修时间服从正态分布，电子类及通信设备损伤的维修时间服从指数分布［7］；

4）伴随保障过程中，维修保障力量未遭到敌方袭击；

5）只考虑对轻损和中损的作战装备修理任务，对作战装备使用人员可自行修复的损伤不予考虑。

1.2 目标函数设定

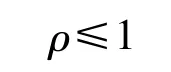
为了避免战时等待维修的装备排队过长，导致出现部分待修装备得不到及时修理的现象，要求该排队系统的服务强度ρ，即单位时间内产生的待修装备数量与维修保障装备能够修复的装备数量的比值：

当ρ=1 时，即刚好完成维修任务而不出现维修保障装备数量过多或者不足的情况，设此时使用的维修保障装备的数量为c1。

为满足战斗的时效性，要求维修保障装备必须在规定的时间T*内到达现场进行修理，即待修装备平均等待时间T'≤T*［7］，设满足此需求的维修保障装备数量为c2。

综合考虑以上两点，得到战时维修保障装备最佳数量为c=max（c1，c2）。要确定c1、c2，首先要得出待修装备平均等待时间T'。

1.3 装备机械装置损伤情形下平均等待时间T'

其中，Ls为等待修理和正在修理的装备数量之和，m为待修装备数量。

对于机械装置损伤的待修装备，其维修时间服从正态分布，已知战场损伤维修时间的期望值为E［T］，方差为Var［T］，根据文献［6］可得：

由P-K 公式，可计算出等待修理和正在修理的装备数量之和Ls，即：

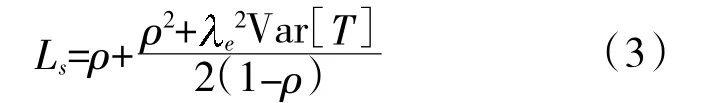
根据Little 公式可得到待修装备平均等待时间T'为：

1.4 装备电子类及通信设备损伤情形下平均等待时间T'

设维修保障装备平均修复率为μ，则该排队系统的服务强度ρ 为：

根据相关资料和理论推导，得到有n 个装备出现损伤的稳态概率Pn为：

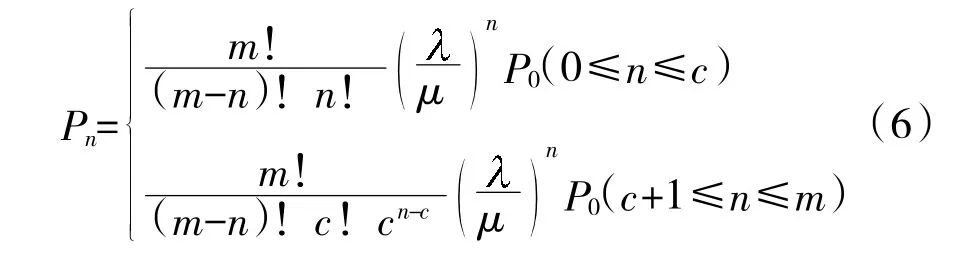
其中，P0为维修保障装备处于空闲时间的概率，表示为：

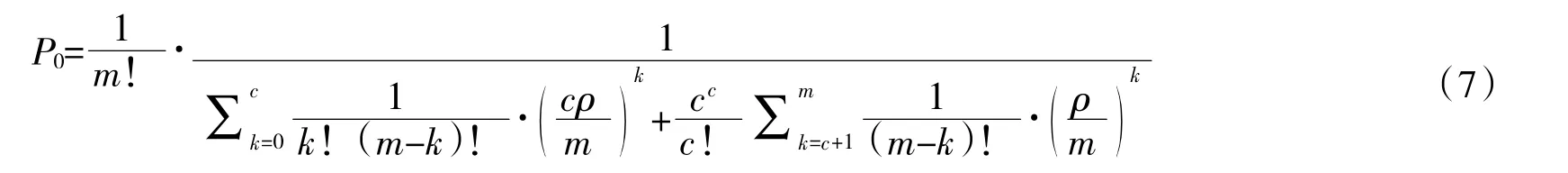
则等待修理和正在修理的装备数量之和Ls为：

等待修理的装备数量Lq为：

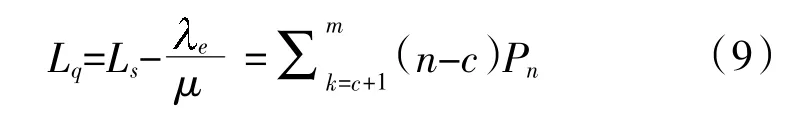
根据Little 公式可得到待修装备平均等待时间T'为：

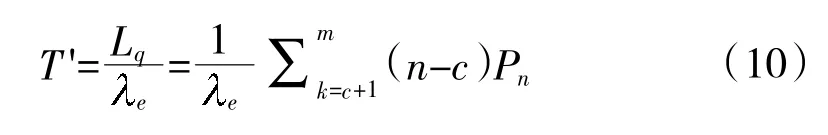
2 装备损坏强度计算

若想知道待修装备平均等待时间T'，首先要得到不同作战装备的损坏强度。因此，下面构建基于信息主导因素的兰彻斯特方程模型对装备受击损坏强度进行预测。

2.1 基于信息因素的兰彻斯特方程模型构建

模型假设：同级别的作战力量所发挥的战斗效能是相同的，同级别的作战力量信息获取、处理能力不一定相同。

传统的兰彻斯特方程有两种表示方式，第1 种是战斗双方兵力互相隐蔽，运用面火力对对方进行杀伤，其数学模型为［8］：

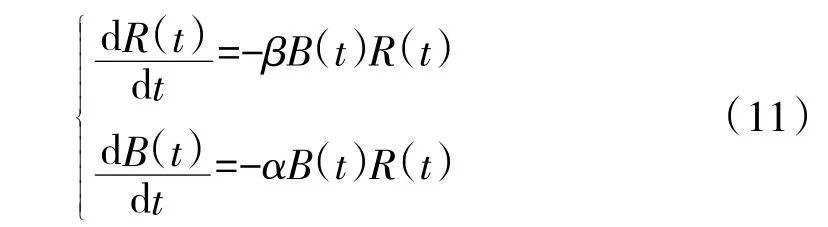
其中，R（t）、B（t）分别代表在t 时刻红方、蓝方所拥有的战斗单位数量，α、β 分别为红蓝双方战斗力系数。

第2 种是战斗双方在完全暴露的情况下，运用火力对特定装备进行精确打击，其数学模型为［8］：

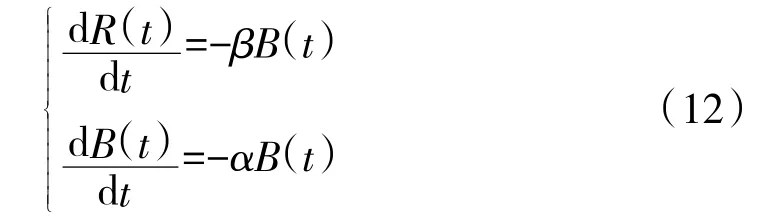
其中，R（t）、B（t）分别代表在t 时刻红方、蓝方所拥有的战斗单位数量，α、β 分别为红蓝双方战斗力系数。

在此基础上，引入变量Ir、Ib，分别表示红蓝双方的信息获取及处理能力，对传统的兰彻斯特方程进行改进得到：

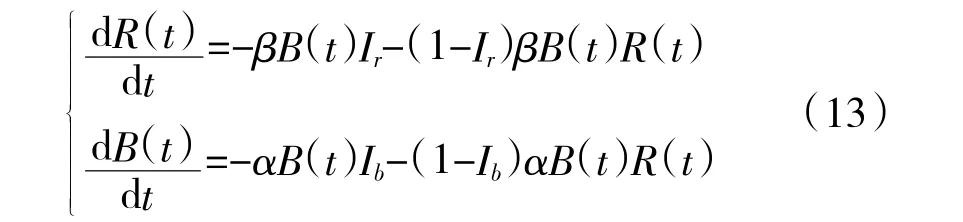
式中，Ir、Ib分别为红蓝作战双方信息获取处理能力系数，信息获取处理能力就是作战双方运用信息系统获取信息优势，并将信息优势转化为决策和行动优势的能力。其中，0≤Ir≤1、0≤Ib≤1。α、β 分别为红蓝双方战斗力系数。

当Ir=Ib=0 时，红蓝作战双方均没有信息获取处理能力，即双方处于互相隐蔽状态，代入上式则符合传统兰彻斯特方程第一种情形。当Ir=Ib=1 时，红蓝双方均具有最好的信息获取处理能力，即双方处于完全暴露状态，代入上式则符合传统兰彻斯特方程第2 种情形。

2.2 装备受击损坏强度受击计算

设在一次典型的进攻作战行动中，敌我双方参战部队的初始兵力分别为M2、M1，红军装备总体受损率为D，战斗结束时双方兵力分别为M20、M10。

则：

则第i 类作战装备受击损坏率Di为：

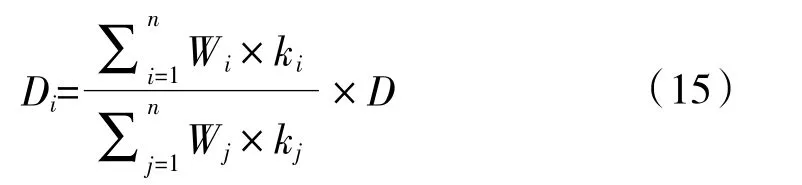
其中，Wi表示第i 类作战装备的数量，n 是所有作战装备的种类，kj表示第j 类作战装备的受击权重。

由已知假设，战场损伤规律符合指数分布，因此，装备的受击损坏强度受击为：

T 表示作战时间。

2.3 装备技术故障损坏强度技术计算

作战装备的技术损坏率就是装备故障率，一般采用平均故障间隔里程或平均故障间隔次数来衡量。为方便研究，假设装备的技术损坏概率服从指数分布，则第i 类作战装备技术损坏率Fi为：

式中，si为第i 类作战装备实际使用里程或使用次数，θi表示第i 类作战装备平均故障间隔里程或者平均故障间隔次数。因此，在一次战斗中，装备单位时间的平均技术损坏强度

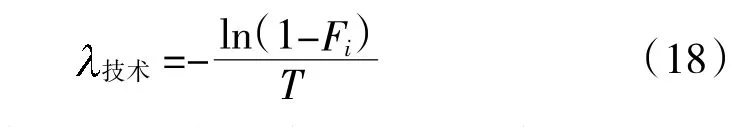
假设装备出现受击损伤和技术损伤是相互独立事件，则作战装备的损坏强度

3 示例应用

3.1 装备受击损坏强度受击及技术故障损坏强度技术计算

假设在某一次进攻战斗中，已知我方通过先进的信息侦察手段部分获取了敌方部署位置、兵力大小以及敌攻击强度，敌方也有较好的信息反侦察能力，设双方信息获取处理系数Ir、Ib分别为0.8、0.6；双方战斗效能系数α、β 分别为0.3、0.4。

查阅文献［11-12］并对数据进行相关处理得到我方和敌方在此次战斗中主要作战装备和受击权重，以及我军装备受击损坏程度分布如表1、表2 所示。由表1 可知，双方初始等效兵力M1'、M2'分别为914、648；当敌方兵力损失达到了2/3 时，战斗即认为结束。

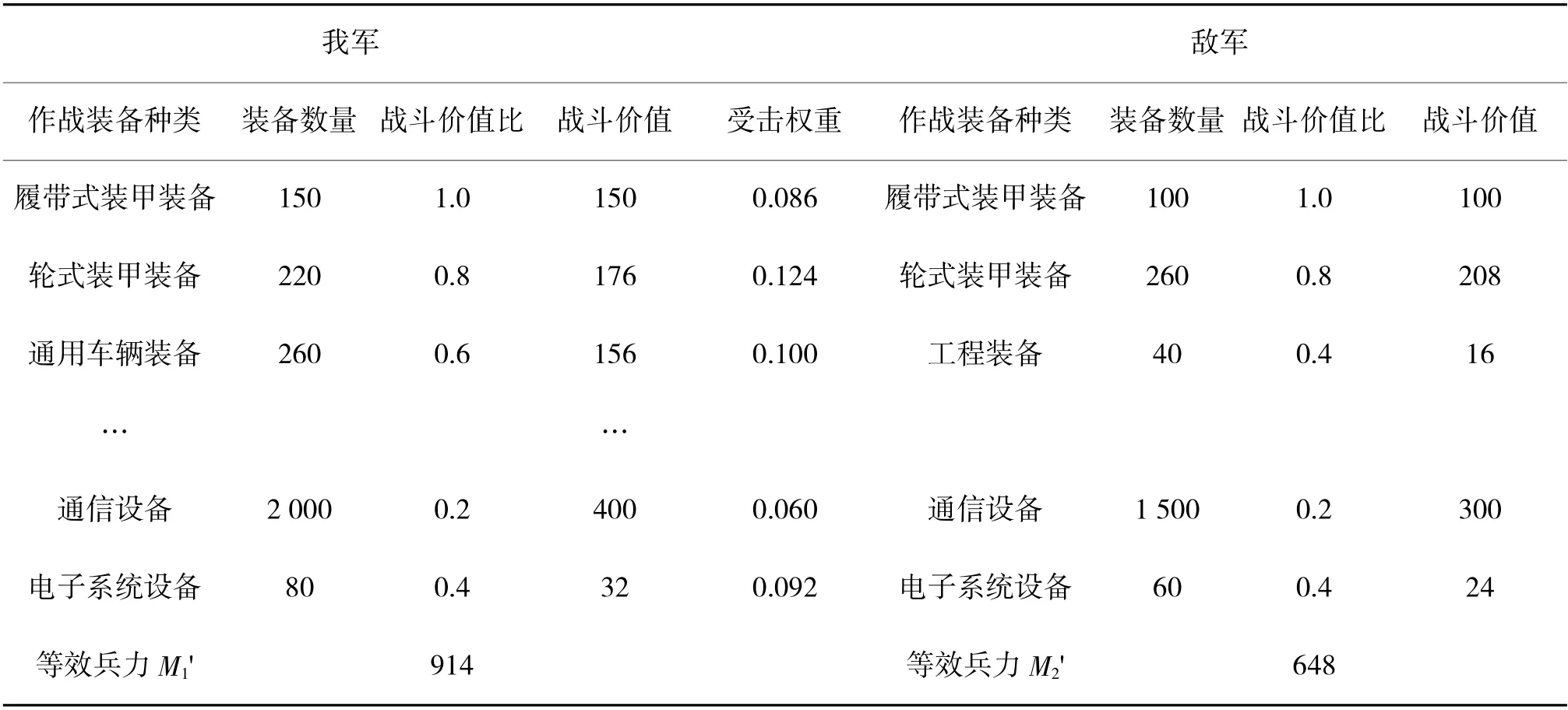
表1 作战装备战斗价值和损坏程度区分

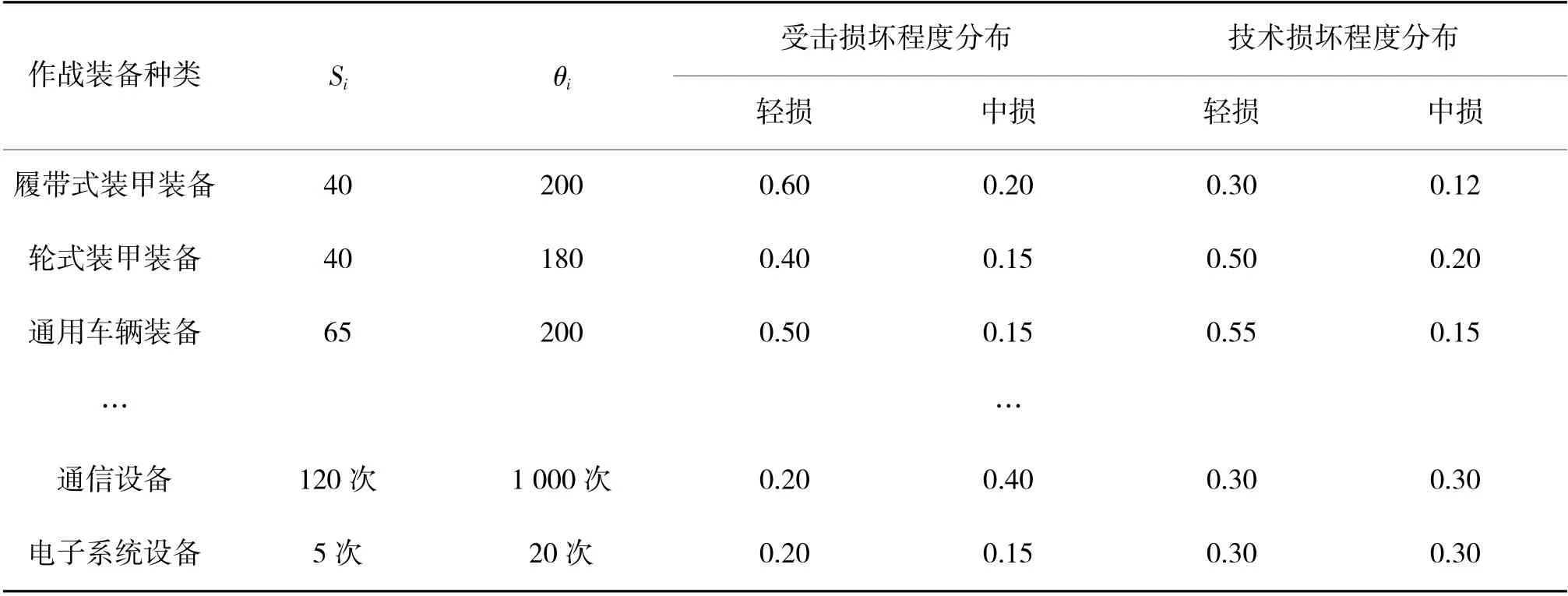
表2 我军装备受击损坏程度分布

利用Matlab 软件对该次进攻战斗进行仿真，结果如下页图1、表3 所示。

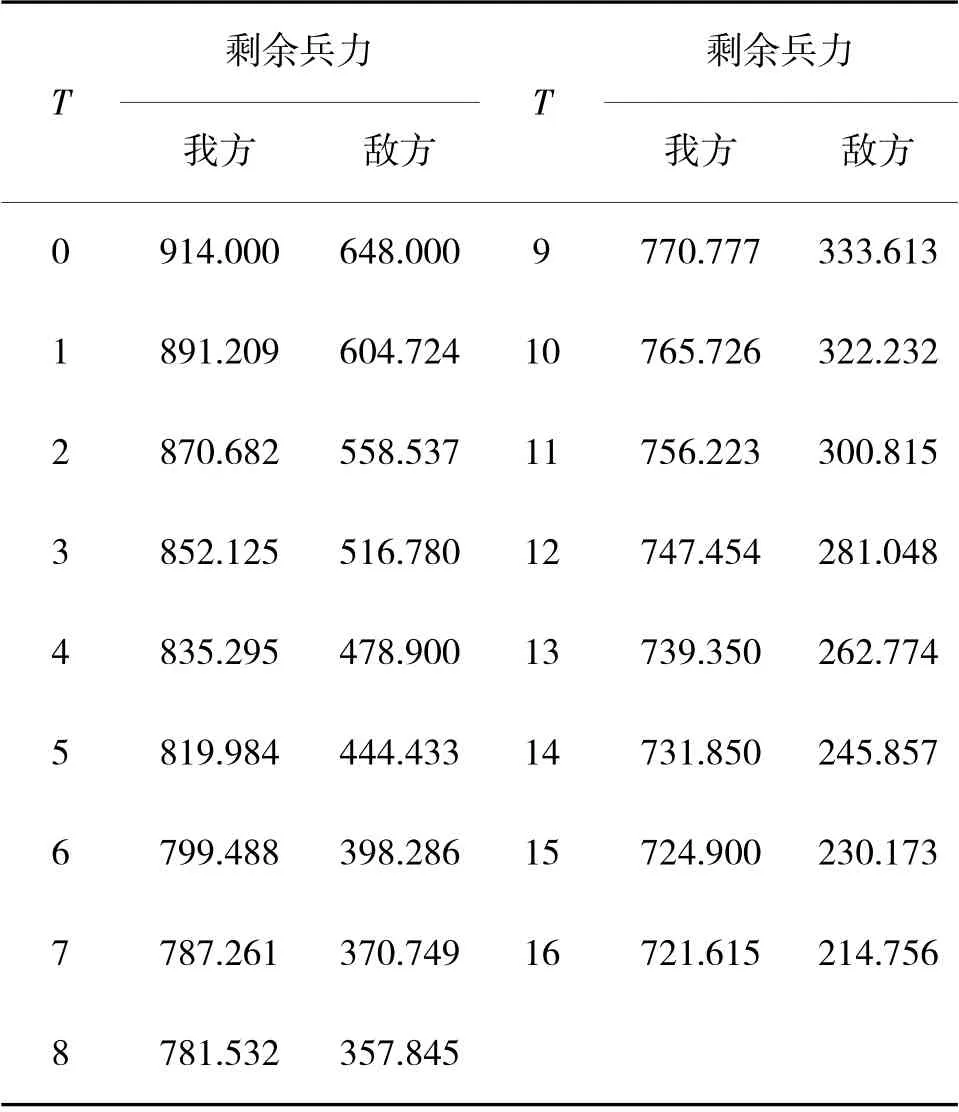
表3 双方战斗剩余兵力数据表

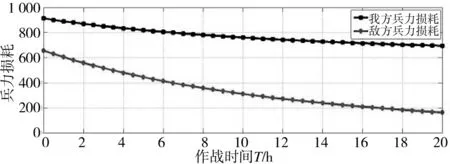
图1 双方兵力损耗变化

从表3 我方与敌方兵力变化可以得到，当战斗进行至16 h 时，敌方兵力损失达到了2/3，此时认为我方战斗取得胜利。此时，我方兵力大小为M10=721.615，根据式（14）可得，我方作战装备总的受击损坏率D 为：

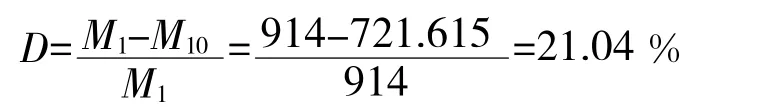
由式（14）～式（18）计算出我方各类作战装备受击损坏率及受击损坏强度和技术损坏率及技术损坏强度，根据表1 和表2 提供的作战装备数量计算出受击、技术，以及我方在此次进攻战斗中各类武器装备的损坏数量，向上取整，结果如表4 所示。

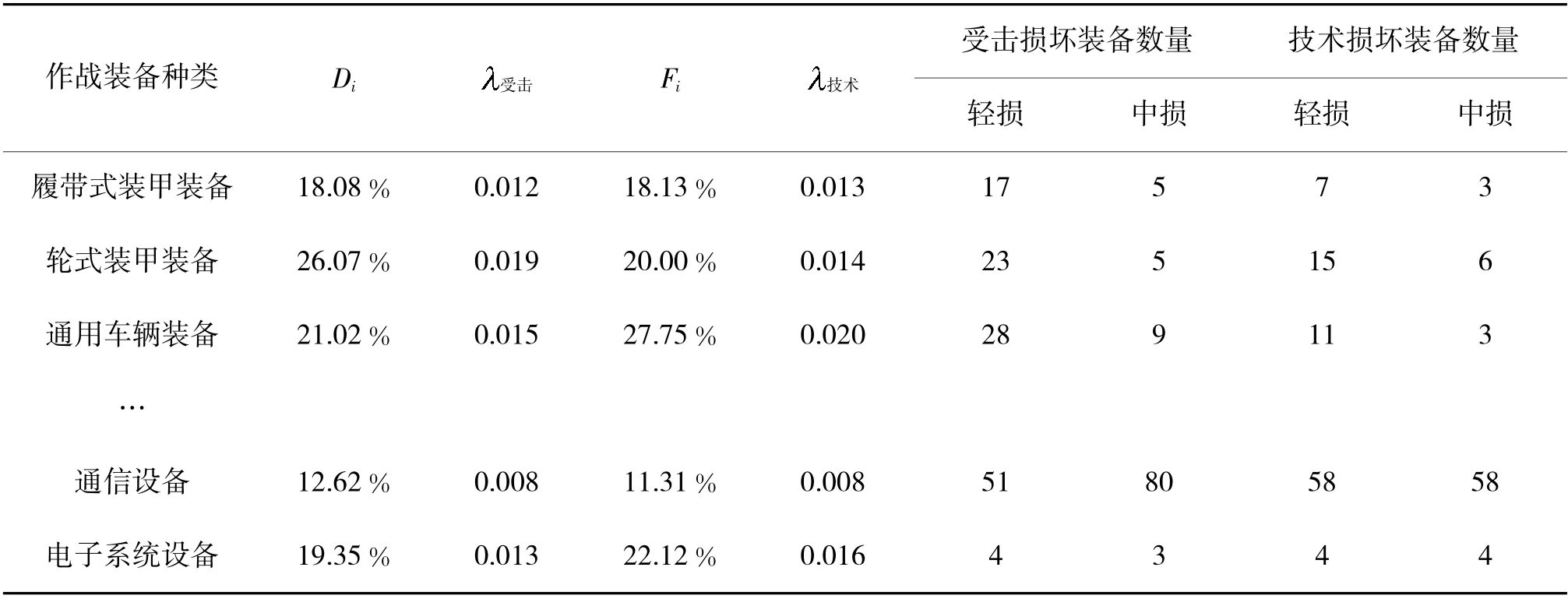
表4 我方此次战斗中作战装备损坏数量

3.2 维修时间为正态分布时的维修保障装备数量

对于履带式装甲装备的损伤，主要是底盘和武器系统受损，使用装甲拆装工程车和火炮修理工程车两种保障装备进行战场抢修。已知装备机械装置的平均维修时间服从正态分布，其参数分别为［7］

E［T1］=3.5，Var［T1］=0.12；E［T2］=3.2，Var［T1］=0.21

战时抢修时，规定轻损装备在2 h 内修复，中损装备在4 h 内修复。以履带式装甲装备为例，首先计算轻损装备维修底盘时所需要的装甲拆装工程车的数量，令平均维修时间T1'=1 h，根据式（1）、式（2）计算可以得到等待抢修和正在抢修的装备数量之和Ls1=2.43，代入式（3）可得

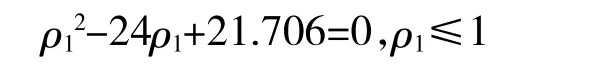
解得ρ1=0.796。代入式（2）计算可得需要装甲拆装工程车的数量

当ρ1=1 时，

因此，维修底盘的装甲拆装车的最佳数量为c拆装车=max（c1拆装车，c2拆装车）=2.37，向上取整，即轻损装备需要维修底盘的装甲拆装车的最佳数量为3 台。

令拆装工程车对中损装备的平均维修时间T2'=3 h，根据式（1）～式（4）可计算得到

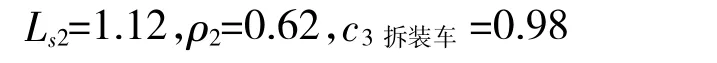
当ρ2=1 时，c4拆装车=0.60。

因此，对于中损装备所需装甲拆装车为c拆装车=max（c3拆装车，c4拆装车）=1.15，向上取整，即1 台。

武器系统损伤主要包括火控系统、炮控系统等损伤，维修时间较短；令火炮维修工程车的平均维修时间为0.4 h，根据式（1）～式（4）可分别计算得到轻损、中损装备的

Ls轻=1.98，Ls中=0.66；c1工程车、c2工程车分别为2.35，1.39，当服务强度都取1 时，其所需工程车数量分别为1.76，0.64，取最大值并向上取整可得轻损、中损分别需要得维修工程车为3 台、2 台。

同理，可对轮式装甲装备、通用车辆装备进行所需保障装备数量计算。

3.3 维修时间为指数分布时的维修保障装备数量

对于电子类及通信设备的损伤，其修复时间服从μ=0.251 9 的指数分布［7］。以电子类设备为例，当服务强度ρ=1 时，根据式（5）计算可得c=1.726 8。令待修装备平均等待时间T '≤1.5 h，根据式（6）～式（10）及利用Matlab 计算得到c、Ls、T'的关系，如表5 所示。

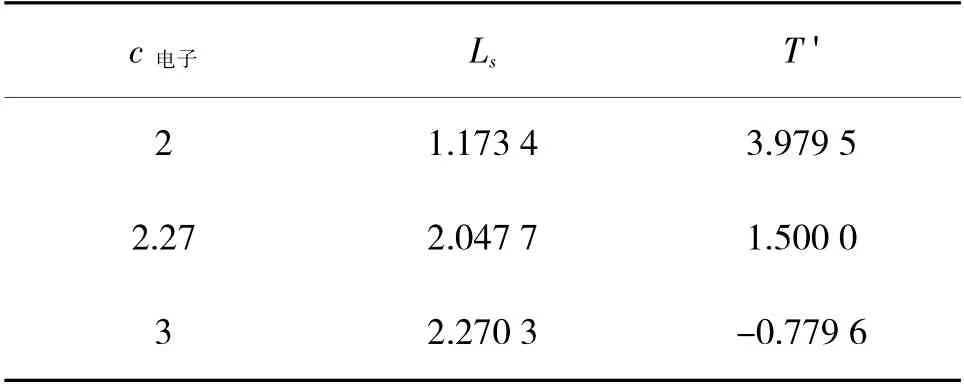
表5 c、Ls、T'关系

从表5 可以看出，随着电子维修设备的数量增长，待修装备进行修复的平均时间降低。当电子维修设备数量为3 时，符合T'≤1.5 h。根据式子可得

c电子=max（c1电子，c2电子）=max（1.726 8，3）=3

同理，可计算得出通信设备所需的维修保障装备数量。

4 结论

本文采用排队论和基于信息因素的兰彻斯特方程的方法，对在一次典型的进攻战斗中的作战装备所需维修保障装备数量进行了确定。通过分析不同的待修装备其维修时间服从不同的分布，依照建立的不同计算模型进行维修保障装备数量计算，根据战场的时效性确定了维修保障装备数量。此外，本文结合目前信息化条件对战场进程的影响，对传统的兰彻斯特方程进行优化并计算出装备受损率。基于此，对合成部队保障装备的优化配置是下一步的研究重点。