基于变分模态分解的非稳态备件需求预测方法*
2022-01-26秦海峰侯兴明徐庆尧
秦海峰,杨 超,侯兴明,徐庆尧,侯 翔
(1.航天工程大学,北京 101416;2.陆军装甲兵学院士官学校,长春 130117)
0 引言
备件是保持装备处于良好状态的重要物质基础,装备受损后能够及时获取足够的备件进行更换维修,是备件保障的主要目标。然而,备件的过量储备则会导致备件保障人力、经费的浪费,因此,科学准确预测备件需求量是备件配置的重要内容。
在备件需求预测的研究中,时间序列分析由于避免了影响因素调查与筛选、多重共线性等难点而得到广泛应用[1]。一些学者运用求和自回归滑动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)对非稳态需求备件进行预测,并证明了其比传统的移动平均预测法具有更高的预测精度[2-4],但其预测精度需要大量的备件历史数据作为支撑。随着人工智能技术的发展,部分学者运用神经网络预测法对非稳态备件需求进行预测[5-6],可以较好地处理备件需求非稳态的特点,但由于神经网络过分克服学习错误而使模型的泛化能力不强,其预测效果并不是很满意[7]。
近年来,为了有效处理非稳态时间序列的需求,一些学者提出对非态时间序列先进行分解,预测之后再进行结果重构的处理思路,并将信号领域的时频分析方法引入非稳态需求的备件预测研究中,如传统的小波分析法、近年来出现的经验模态分解方法等[1,8],都取得了较好的效果。但小波分析法对小波基的选择要求较高,经验模态分解方法的理论基础较为薄弱,在对数据分解过程易产生模态混叠、端点效应等问题[9]。
科学技术的快速发展及其在装备领域的运用,武器装备型谱多元、技术复杂的特点日益突出。在全军大抓实战化训练的大背景下,装备实战实训活动的广泛展开,大量装备的备件需求较之以往呈现出明显的非稳态、非线性特点,针对上述方法存在的问题,本文尝试引入一种新的非稳态序列的分析方法,并引入模糊熵作为序列的复杂性度量,对分析后的序列数据进行处理,进而运用预测性能较高的径向基神经网络方法对备件需求进行预测建模,以提高非稳态备件需求预测的精度。
1 基于变分模态分解的序列分析
变分模态分解(Variational Mode Decomposition,VMD)理论由Dragomiretskiy 和Zosso 于2014 年首次提出,是信号处理领域一种对信号进行分解和估计的新方法,具有坚实的理论基础,并被成功运用到经济、能源领域的非线性、非稳态时间序列预测中。VMD 能够将一组具有非稳态特征的数据信息分解为多个中心频率不同、带宽有限的模态分量,并通过迭代搜寻变分模型的最优解来使各个模态的估计带宽之和最小。可见,VMD 的核心则是变分问题,本质则是求取条件极值的问题,其算法原理包括变分模型的建立和求解两部分。
1.1 变分模型的建立
设f(t)为一个备件需求量的时间序列,用VMD将其分解为K 个模态函数uk(t)(k=1,2,…,K),使每个模态函数的估计带宽之和最小,并以f(t)与各模态函数之和相等为约束条件,可构建其变分约束模型,步骤如下[10]:
1)对各模态分量进行希尔伯特变换,获得其解析信号

式中,wk为uk(t)的中心频率。
3)对各模态分量的带宽进行估计,以带宽之和最小为目标,则变分约束优化问题可建立如下模型

1.2 模型求解

3)对上式进行傅里叶等距变换进行频域转换
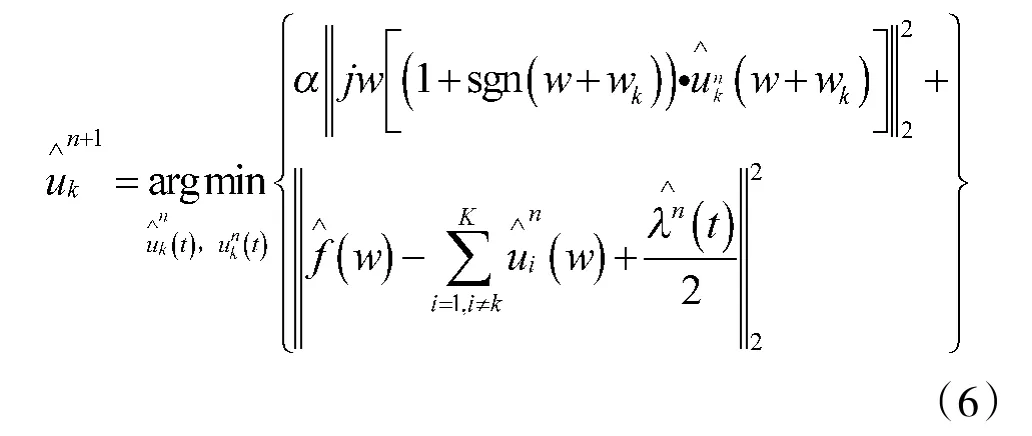
4)将式(6)中第1 项的w 替换为w-wk,得
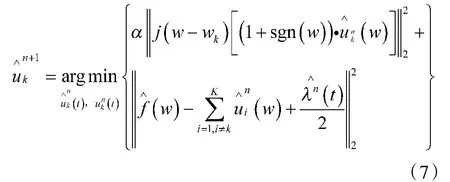
将式(7)转换为[0,+∞]频率区间内的积分形式
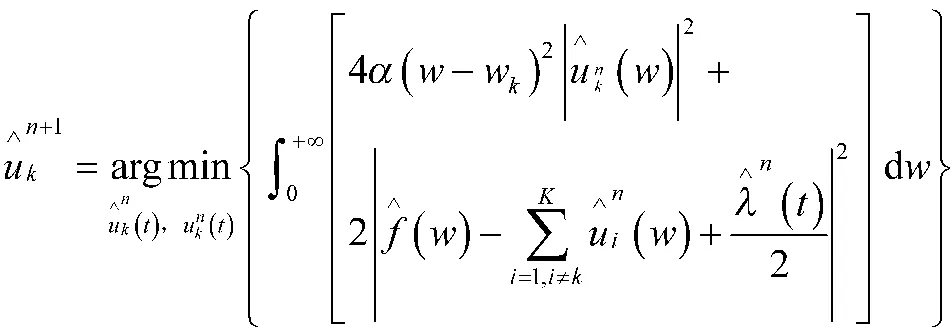
则可得到更新后的优化问题为

1.3 算法流程
综上可得VMD 算法流程,如图1:

图1 VMD 分解算法流程图
1)预估各模态分量个数K 和平衡约束参数α,并对分量函数、中心频率和拉格朗日算子进行初始化;
2)令n=n+1,开始循环;

5)判断是否满足下列收敛条件,若满足,则结束分解;否则返回步骤2)进行下一次迭代。
2 基于模糊熵的分量聚合
对非稳态备件需求的观测值序列进行变分模态分解后,会得到K 个模态分量,如果对所有的模态分量都进行预测,无疑会增加模型的计算量。因此,本文引入基于模糊熵的时间序列分析法,根据分解后模态之间的复杂性和相似性进行分量聚合,减少分量个数,在确保数据信息能够反映备件需求明显特征的基础上,提高模型计算的效率。
模糊熵是用以量化时间序列复杂程度的一种度量方法,是对近似熵和样本熵的改进[11-13],它既继承了近似熵和样本熵在描述时间序列复杂程度上的长处,又解决了二者因数据的绝对值差判断向量相似性所产生的数据小幅波动时分析误差较大的不足,通过对向量相似性进行模糊化的定义,获得较为精确的熵值,进而提高对时间序列分析的精度。基于模糊熵分量聚合步骤为[14-15]:

4)对除自身以外的所有隶属度求平均值

5)迭代更新m 为m+1,重复步骤2)~步骤4);
6)计算模糊熵
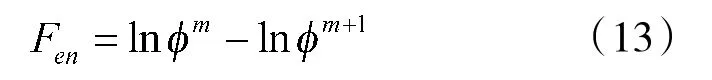
7)根据计算的模糊熵值,对相似分量序列进行叠加合并,实现分量的聚合。
3 径向基神经网络预测原理
径向基神经网络是一种基于多维变量插值的径向基函数(Radical Basis Function,RBF)的神经网络模型[16],它具有结构简单、收敛快速、训练简洁等特点,对任意非线性函数具有较好的逼近能力。因此,RBF 神经网络被广泛应用于时间序列分析、非线性控制和图像处理领域。
RBF 神经网络的结构[16]是一种3 层前向网络,分别为输入层、隐藏层和输出层,各相邻层之间通过神经元连接。其基本思想就是用RBF 作为隐藏层中神经元的变换函数,它的特点是对中心点径向对称且衰减的非负非线性局部响应函数,能够对输入矢量中低维的输入数据变换到高维空间,将低维空间中的非线性问题在高维空间内线性可分。
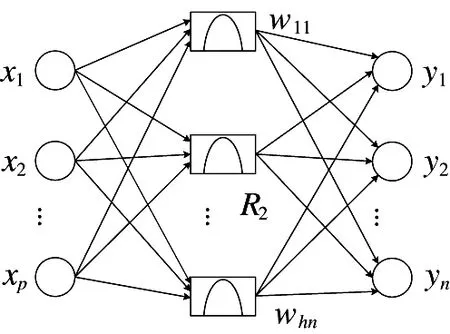
图2 径向基神经网络结构
本文选择RBF 神经网络中常用的高斯函数作为径向基函数,因此,当隐藏层神经元输入变量为备件需求序列xp时,其输出为
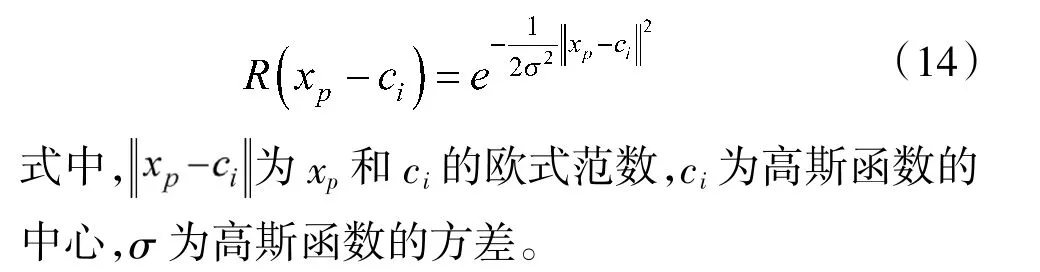
输出层网络相对应的节点j 的备件需求预测序列输出为

式中,wij为隐藏层到输出层神经元的连接权值,i=1,2,…,h 为隐藏层节点数。
由上述RBF 神经网络预测原理,其预测性能的关键在于高斯函数的中心和神经元连接权值的选取,本文采用文献[17]中K-均值聚类算法求取基函数的中心、最小二乘法求取神经元连接权值。
4 预测方法流程
基于变分模态分解的非稳态需求备件预测模型,首先对备件需求量数据的时间序列进行变分模态分解,根据模态分量的模糊熵进行分量聚合,然后将各模态分量序列与备件需求量关系密切的影响因素量化数据共同作为径向基神经网络的输入进行训练,最后进行分量预测,并把各分量预测结果进行数学相加,便得到备件需求量的最终预测值,如下页图3 所示。

图3 基于变分模态分解的非稳态需求备件预测流程
5 案例分析
鉴于实战实训备件保障中历史数据较少和保密要求,以文献[8]中典型的非稳态备件历史数据为输入,如表1 所示,验证分析本文提出的非稳态需求备件预测方法的有效性和精确性,待有效获取部队备件历史数据,或在保密环境下进行本文方法的实际运用,进而支撑部队备件配置决策。
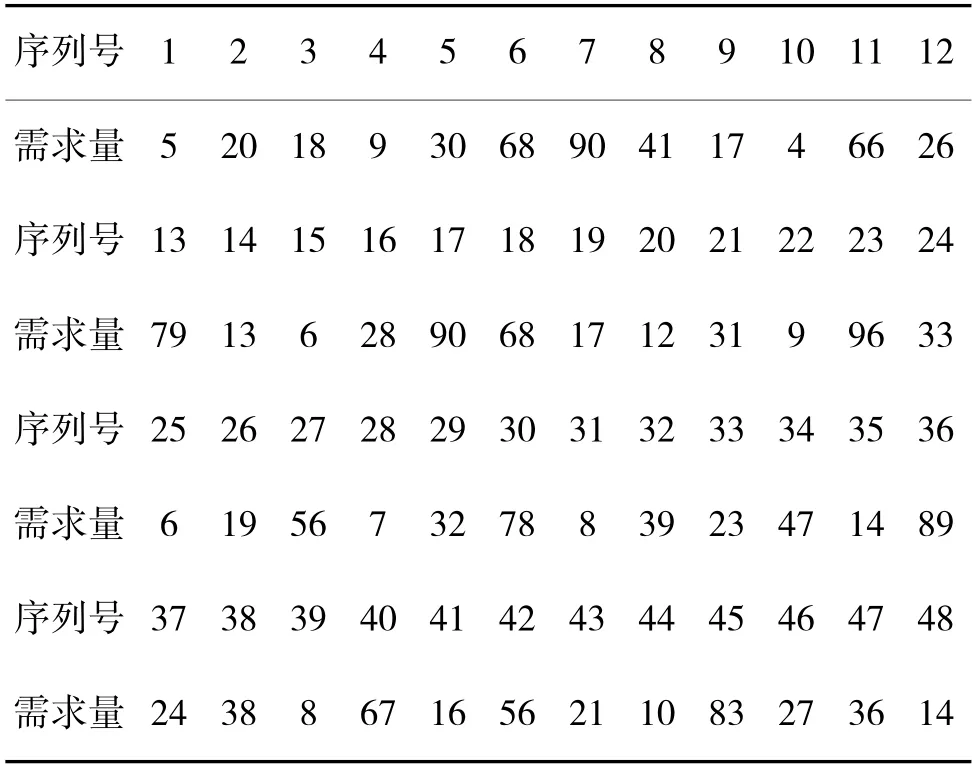
表1 备件原始需求序列
5.1 备件需求序列的变分模态分解
由于受到气候、温度、湿度、使用强度等多种因素的共同影响,使得备件需求的波动较大,如图4所示,直接进行需求序列的分析,难以挖掘备件需求的规律,结果误差较大。首先运用VMD 对备件原始需求序列进行变分模态分解,将备件需求的周期性、平稳性和随机性特征有效地分解,能够更加清晰地认清备件需求的规律,进而进行准确的分析和预测。

图4 原始备件需求波动曲线
由前文可知,对原始备件需求序列进行变分模态分解的关键预估各模态分量个数K 和平衡约束参数α,本文以分量之和与原始序列的平均相对误差为最小为目标,运用MATLAB 编程进行迭代优化寻优,其中,按照一维数据分解的最大边界进行参数寻优范围设置,2≤α≤1 000,2≤K≤15,经计算机自动寻优后得到预估模态分量个数K=14,α=72。
5.2 分量聚合
由图5 可知,预估模态分量个数较多,如果对每个分量都进行预测计算量是很大的,随之也会产生较大的累积误差。因此,计算各分量模糊熵,各分量模糊熵值见下页表2 所示。

图5 原始备件需求序列VMD 分解后的分量示意图

表2 各分量模糊熵值
以模糊熵为基准,按照熵值阶跃不超30,跨度不超60 进行分量聚合,可将14 个原始模态分量聚合得到8 个模态分量,即分量3 和4 聚合,分量6、7、8 聚合,分量9、10 聚合,分量12、13、14 聚合,聚合后各分量示意图如图6 所示。

图6 基于模糊熵聚合的分量示意图
由聚合后的分量示意图可以明显看出,新的模态分量序列尺度特征较为明显,IMF-1、IMF-2、IMF-3、IMF-4 波动性较大,体现出了在短期多种随机因素和不确定性因素影响下的备件需求的变化;IMF-5、IMF-6、IMF-7 周期性较为明显,体现出了备件需求存在一定的规律性;IMF-8 相对平稳,体现了备件需求变化的长期趋势。
5.3 备件需求预测
5.3.1 模型训练与分量预测
基于备件序列模态分量明显的多尺度特征,按照径向基神经网络的预测原理对每个分量进行预测。以训练误差平方和(SSE)为目标,选择8 个备件序列分量的前43 个数据对RBF 神经网络预测模型进行训练,训练参数设置为:SSE=1×10-12;扩展系数spread 设为80;最大神经网络个数默认设为与训练样本个数相同,同时,以各序列最后5 个时点的备件需求作为验证数据对预测结果进行检验,各分量分解值与预测值对比情况如图7 所示。

图7 各分量实际值与预测值检验对比图
由检验对比图可明显看出,训练好的预测模型能够很好地对备件需求各模态分量实施预测。具体来看,各预测时点预测误差平方和如表3 所示。

表3 各预测时点预测误差平方和
5.3.2 分量叠加与预测结果分析
根据变分模态分解的基本原理,将备件需求各模态分量最后5 个时点的预测值分别相加,便可得到最后相应时点备件的预测数量。同时,本文选取MSE 和MAPE 作为误差分析指标,将预测结果分别与文献[8]提出的集合经验模态分解(EEMD)-支持向量回归(SVR)预测法,以及动态神经网络和ARIMA 等3 种非线性预测方法进行比较分析,通过下页表4 中误差指标数据,提出的VMD-模糊熵-RBF神经网络预测模型的精度要明显高于其他方法,同时证明该方法对于非稳态需求的备件预测具有较强的适用性,既能有效处理非稳态的备件需求时间序列,挖掘深层次的备件需求规律,又能大幅提高备件预测的精度,尤其适用故障机理复杂、高价值备件的新型航天装备备件需求预测。

表4 预测结果对比分析
6 结论
针对非稳态备件需求,引入信号领域的时频分析方法,运用变分模态分解将非稳态备件序列进行分解,挖掘备件需求的周期性、平稳性和随机性模态,并基于模糊熵对分量进行聚合,进而运用径向基神经网络进行分量预测和备件需求量的聚合生成,通过案例实验,证明了本文提出的方法相较于现有研究所提出的方法,具有明显的精度优势和较强的适应性,能够较好地匹配装备非稳态备件需求特性,提高备件需求预测的精度,进而提高备件保障效率。
