基于ACSOA-BP神经网络的瓦斯含量预测模型

赵 伟，陈培红，曹 阳

（1.河南能源化工集团永煤公司 陈四楼煤矿，河南 永城476600；2.中国矿业大学（北京）应急管理与安全工程学院，北京100083）

随着煤矿开采深度和强度增加，瓦斯灾害防治工作面临严峻挑战。瓦斯含量预测是矿井瓦斯灾害防治与综合利用的重要依据，我国煤盆地沉积体系和构造格局的时空差异，导致瓦斯赋存具有复杂性、动态性、随机性和多因素影响等特征，无法通过简单计算准确求解各影响因素的权重，不利于瓦斯含量的准确预测[1-5]。相关专家将多元回归、支持向量机、神经网络等模型用于瓦斯含量预测，并提出了相应改进方法提高瓦斯含量预测的准确性[6-7]。BP神经网络模型以其初始参数选择简单、非线性映射能力强、样本数据容错性高和预测精度较高的特点，在预测研究中应用广泛[7-10]。随着计算机科学的发展，粒子群算法[6]、鲸鱼算法[11]和海鸥算法[12-13]（Seagull Optimization Algorithm,SOA）等智能优化算法以其收敛速度快、寻优能力强等特点，被用于优化模型参数，提升模型预测精度。其中，SOA算法具有结构简单、参数少、收敛速度快等特点，但该算法存在全局搜索能力弱、易陷入早熟收敛和种群多样性差等问题[14]。混沌是一种无规则的运动状态，具有随机性、遍历性和非线性等特点，被用于增强智能优化算法的全局搜索能力[15]。陈四楼煤矿属煤与瓦斯突出矿井，井田内二2煤层瓦斯含量受多因素共同作用，空间分布规律复杂，瓦斯含量预测准确性较低，制约了矿井瓦斯灾害的精准防治。综合分析多种因素对瓦斯含量的影响，将混沌算法与海鸥算法融合，通过对种群进行混沌初始化，引入自适应混沌算法，促使陷入早熟收敛的个体进行混沌搜索，引导其跳出局部极值；并采用非线性收敛因子引导海鸥搜索过程，提高寻优精度和速度。将改进的自适应混沌海鸥算法用于BP神经网络权重和阀值优化，建立基于ACSOA-BP神经网络的瓦斯含量预测模型。

1 瓦斯含量影响因素

1.1 瓦斯含量基础数据

陈四楼煤矿位于河南省永城市，属华北东部Ⅲ级区带[16]，井田内断层大量发育。主采山西组二2煤层，为海湾-碎屑潮坪沉积体系与河控三角洲沉积体系转变过程中沉积，煤层赋存稳定，平均厚度2.45 m；瓦斯含量0.22 ～11.79m3/t，整体小于5m3/t，瓦斯组分以氮气和甲烷为主，呈现南北分异、局部富集的分布特征。选取具有代表性的褶皱、断层、顶板岩性、煤层厚度、煤层埋深等影响因素，及瓦斯含量实测数据作为样本，其中，断层和褶皱分别采用断层分形维数和构造曲率进行定量表征，具体计算方法见文献[17-18]。瓦斯含量及影响因素部分数据见表1。瓦斯含量与各影响因素的关系如图1。

表1 瓦斯含量及影响因素部分数据Table1 Partial data of gas content and influencing factors

1.2 瓦斯含量影响因素

1）褶皱。在永城背斜的基础上，井田内发育周庄向斜、高六湾向斜、李古同背斜等次级褶皱构造，褶皱展布呈隔槽式，向斜构造东翼变形大于西翼，形成于早燕山期NWW向挤压作用背景。陈四楼煤矿井田隔槽式褶皱剖面图如图2。向斜西翼F53、F82等同沉积断层是隔槽式褶皱形成的关键，同时造成向斜核部和东翼含煤地层厚度大于向斜西翼和背斜。侏罗纪以来，背斜隆起上覆岩层剥蚀严重，瓦斯大量逸散。向斜构造变形强烈，NNE向断层密集发育，煤体结构破碎，煤层与顶底板发生相对滑移，构造煤全层发育，核部上覆岩层保存相对完整，有利于瓦斯保存。构造曲率可对褶皱变形和受力状态进行定量表征，二2煤层位于褶皱中和面以下，即正曲率值反映煤层受到挤压应力。瓦斯含量与构造曲率呈正相关（图1（a）），变形强烈且处于挤压应力状态的向斜东翼有利于瓦斯保存，瓦斯含量和涌出量均较高。

图1 瓦斯含量与各影响因素的关系Fig.1 Relationship between gas content and influencing factors

图2 陈四楼煤矿井田隔槽式褶皱剖面图Fig.2 Profile of trough-like folds in Chensilou Coal Mine

2）断层。中新生代伸展构造叠加于早燕山期挤压走滑构造之上，造成井田内断裂构造大量发育，局部可达100条/km2，并构成NNE向-NWW向网格状裂隙系统。现今构造应力场最大主应力方向为NE76.46 °～83.77 °，NNE向断层和NWW向断层分别为压扭性和张扭性，具有不同的瓦斯封闭能力[19]；井下观测发现，同等规模条件下NNE向断层附近构造煤规模大于NWW向断层，NNE向断层附近瓦斯含量较高，瓦斯含量与断层分维值呈正相关（图1（b））；NWW向断层整体呈开放性，60%的矿井突水与NWW向断层有关，煤层沿断层发育一定宽度的风化带（俗称黄矸），附近区域瓦斯含量相对较低，瓦斯含量与NWW向断层分维值呈负相关（图1（c））。不同封闭性断层的差异分布导致了局部瓦斯富集，井田内高六湾向斜东翼和高后口向斜东翼瓦斯富集区内NNE向断层分形维数值分别为1.54 和1.60 ，NWW向断层分形维数均在1.30 以下。

3）顶板岩性。煤层顶板的透气性直接影响上覆地层对瓦斯的垂向封闭能力，煤层顶板的透气性越低，瓦斯越容易保存。该矿二2煤层顶板为泥岩、砂质泥岩、细粒砂岩和中粒砂岩构成的互层结构，发育多个泥岩封盖层，构成复杂的封闭系统，随着顶板20m内泥岩厚度的增加，煤层瓦斯含量整体呈增大趋势（图1（d））。

4）煤层厚度。煤层提供了瓦斯生成的物质基础和赋存空间，同等条件下，煤层越厚瓦斯生成总量和储存量越大。该矿二2煤层属中等变质无烟煤，厚度为0.8 ～3.85m，平均厚度为2.45m，具有较好的原始瓦斯生成能力和储存能力。由于瓦斯大量逸散，二2煤层厚度与瓦斯含量相关性不显著，但高瓦斯含量区域均位于同沉积断层上盘，煤层厚度大于2.5m（图1（e））。

5）煤层埋深。侏罗纪以来，含煤地层整体处于抬升剥蚀阶段，二2煤层埋深为311～898m，瓦斯含量整体小于5m3/t。NWW向断层将井田分割为不同的地质块体，瓦斯地质特征存在较大差异。井田北部主体地质构造为NNE向高流湾向斜、周庄向斜和NWW向F13、F18断层，构造变形强烈，八采区和十二采区西翼受阶梯状断层和隔槽式褶皱控制，小断层大量发育，煤体结构破碎，瓦斯含量较高，实测瓦斯含量最大值11.79m3/t，但埋深为459～620m；井田南部煤层由东向西埋深逐渐增大，深部五采区、九采区和十五采区埋深为600～920m，开放性NWW向断层密集发育，水力运移作用下瓦斯大量逸散，实测瓦斯含量最大值4.94m3/t，低于八采区和十二采区西翼，导致井田内瓦斯含量与埋深相关性较差（图1（f））。

2 ACSOA-BP神经网络预测模型

2.1 基本原理

2.1.1BP神经网络的基本原理

BP神经网络是一种按照误差逆向传播算法训练的前馈性神经网络，采用梯度下降法反复训练样本修正权值和阀值，实现对不同维度空间的非线性映射，对非线性样本具有较好的适应性[20]。BP神经网络包括输入层、隐含层和输出层，其数学表达式为：

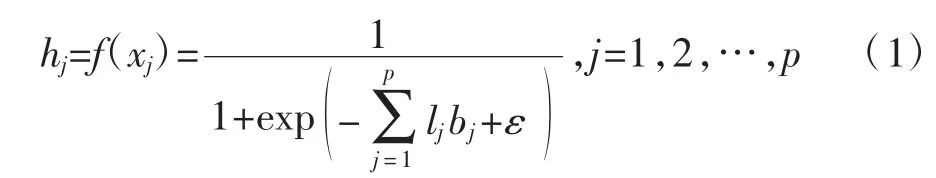
式中：hj为输出值；f（x）为激活函数；xj为输入值；lj为隐含节点的连接权值；bj为隐含节点间的阀值；ε为隐含节点的阀值；p为隐藏节点数。

2.1.2SOA算法的基本原理

SOA算法是Dhiman等于2019年提出的一种新型智能优化算法，根据自然界海鸥的迁徙（全局搜索）和攻击（局部搜索）行为建模，通过迭代计算寻找全局最优解[12]。

2.1.2.1 迁 徙

该阶段通过效仿海鸥群体的迁徙行为实现全局搜索，迁徙过程中满足避免碰撞、最佳位置方向和靠近最佳位置等3个条件：

1）避免碰撞。

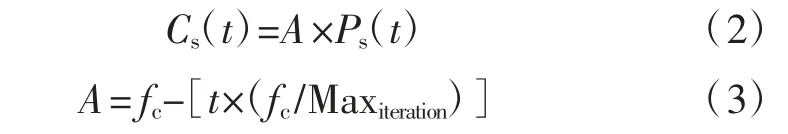
式中：Cs（t）为不与其他海鸥碰撞的新位置；A为收敛因子，随迭代次数t从2线性递减到0，避免碰撞的发生；Ps（t）为海鸥现在的位置；t为当前迭代次数；fc为超参数，取定值2；Maxiteration为最大迭代次数。

2）最佳位置方向。

式中：Ms（t）为最佳位置的方向；B为平衡全局和局部搜索的随机变量；Pbs（t）为海鸥最佳位置；rd为［0，1］范围内的随机数。

3）靠近最佳位置。在避免碰撞后，海鸥向最佳方向移动，到达新的位置Ds（t）（搜索全局最优解）。

2.1.2.2 攻 击

该阶段通过改变攻击角度和速度，以螺旋状运动方式逐渐收缩包围攻击猎物，具有较强的局部搜索能力，x、y、z平面中运动的数学模型如下：

式中：r为每个螺旋的半径；θ为［0，2π］范围内的随机值；u、v为决定螺旋形状的相关参数。

海鸥的攻击位置Ps（t）计算如下：

2.1.3ACSOA算法的基本原理

1）混沌初始化种群。SOA算法初始种群选取决定了初始Pbs值，直接影响了算法搜索的平衡性和准确性，但该算法初始海鸥种群选取无定则，造成寻优效率低且易陷入局部优化。故引入Logistic混沌映射初始化种群[21]，增强算法性能。

式中：Zi为第i个变量，Z0∈［0，1］；μ为控制参量，当μ=4时，系统处于完全混沌状态，其混沌空间为［0，1］。

2）自适应混沌映射。SOA算法采用螺旋状搜索增强局部搜索能力，但在接近中心的过程中，个体多样性锐减，寻优效率低且易陷入局部优化。利用混沌对初始解敏感的特点，以适应度为评判指标，当海鸥种群优化搜索陷入早熟收敛状态时，开启混沌搜索，引导种群跳出早熟状态，进一步搜索全局最优解。

式中：Pmin、Pmax为海鸥种群遍历范围的最小值和最大值；f为当前群体的适应度值；favg为每代种群适应度的平均值。

3）非线性函数收敛因子。收敛因子A在算法迭代中发挥着平衡全局和局部搜索的作用，随着收敛因子A降低，全局搜索能力降低，局部搜索能力增加。SOA算法采用线性惯性权重，对A值进行线性递减，以平衡全局和局部搜索能力[12]。但实际搜索是一个复杂的非线性过程，搜索前期需保持较高的全局搜索能力，防止陷入早熟收敛；搜索后期需提升局部搜索能力，提高寻优速度。使用非线性收敛因子Af，替代线性收敛因子A，平滑过渡迁徙和捕食过程，阶段性提升全局和局部搜索能力，提高寻优精度和寻优速度。Af=fc-［fc×（t/Maxiteration）2］。收敛因子A随迭代次数变化趋势如图3。

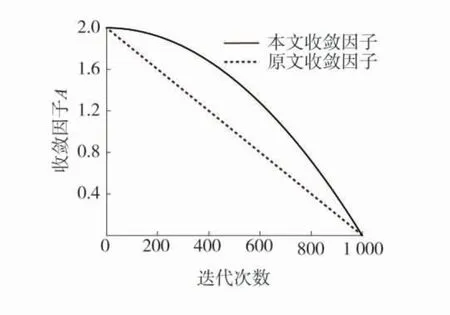
图3 收敛因子A随迭代次数变化趋势Fig.3 Variation trend of convergence factor A with the number of iterations

2.2 模型建立过程

利用ACSOA优化BP神经网络的步骤如下：

1）数据预处理。读取样本数据并归一化，产生训练集和测试集。

2）模型参数设置。根据输入数据特征，设置BP网络模型隐含层节点数、最大迭代次数和终止条件。

3）迭代寻优。对BP神经网络的权重和阀值编码，利用Logistic映射对种群进行混沌初始化，计算并比较种群适应度，更新种群位置，寻找全局最优Pbs（t）和局部最优Ps（t）。达到最大迭代次数或给定适应度时，输出全局最优解Pbs（t）。

4）预测模型建立及运行。建立BP神经网络预测模型，以测试集检验训练后的神经网络，反归一化并输出预测结果。

3 瓦斯含量预测模型应用

3.1 模型参数设置

以35组数据作为样本数据，前30组数据作为训练集，后5组数据作为测试集。根据预测目的和前文研究确定输入神经元为6个，输出神经元为1个。经过反复试算，发现隐含层神经元数量为6时，神经网络训练误差最小，确定BP神经网络的拓扑结构为6-6-1。此外，迭代次数设置为1000次，其它参数采用默认值。BP神经网络训练误差见表2。

表2 BP神经网络训练误差Table2 Training errors of BP netural network

3.2 模型训练与预测结果

为检验ACSOA-BP模型对瓦斯含量的预测性能，选用SOA-BP模型和BP模型与其进行比较，其中，ACSOA算法和SOA算法设置相同参数。选用平均绝对误差（MAE）、均方根误差（RMSE）和实际值与预测值相关系数R评价模型的性能。瓦斯含量预测结果对比见表3。各算法性能指标见表4。不同优化算法迭代曲线如图4。

图4 不同优化算法迭代曲线Fig.4 Iteration curves of different optimization algorithms

表3 瓦斯含量预测结果对比Table3 Comparision of gas content prediction results

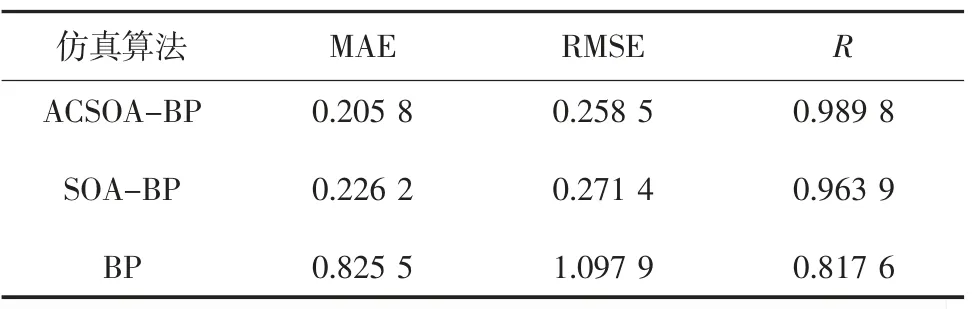
表4 各算法性能指标Table4 Performance index of each algorithm

SOA算法在3次迭代后即到达0.116 的最佳适应度，过低的迭代速度将导致抽样不充分，造成输出参数并非为最优解。ACSOA算法适当增加迭代次数，可有效提升ACSOA-BP模型寻优能力和稳定性。

与SOA-BP模型和BP模型相比，ACSOA-BP模型的误差整体较低，且最差预测值的相对误差和绝对误差均小于其它模型，与实际值最接近；模型预测平均绝对误差、均方根误差和实际值与预测值相关系数R分别为0.2058 、0.2585 和0.9898 ，各性能指标均为最优，具有较高的学习能力和预测精度，可满足瓦斯含量准确预测的需要。

4 结 语

陈四楼煤矿二2煤层瓦斯含量受褶皱、断层和顶板岩性等因素共同作用，瓦斯含量与不同因素呈非线性关系，地质构造是控制煤层瓦斯分布的主要因素。通过对种群进行混沌初始化，并引入自适应混沌算法和非线性收敛因子，提出了ACSOA算法，建立了基于ACSOA-BP神经网络的瓦斯含量预测模型。矿井预测效果表明，ACSOA-BP神经网络模型具有更高的稳定性和预测精度。因瓦斯含量受多因素影响，矿井瓦斯含量预测需增大样本容量，才能提高矿井瓦斯含量预测准确性。