自建点空气质量数据校准的回归模型

加春燕 李 娟 张逸冰 姚 楠 吴嘉豪

(北京工业职业技术学院 基础教育学院，北京 100042)

0 引言

空气污染会给生态环境和人类健康带来巨大危害，因此实时监控空气质量非常重要。国家检测控制站点(简称国控点)通过对“两尘四气”(PM2.5，PM10，CO，NO2，SO2，O3)浓度的监控，可以及时掌握空气质量，进而对污染源采取相应的控制措施[1]。然而国控点成本较高、数量较少、数据发布时间滞后，无法给出实时空气质量的监控和预报。某公司研发的微型空气质量检测仪(简称自建点)成本较低，能对某一地区空气质量进行实时网格化监控，同时能够检测出温度、风速、湿度、气压、降水5种气象参数，但是由于仪器测量误差、气象因素影响等原因，自建点采集的数据有一定误差，需要参照国控点数据对自建点数据进行校准，使得校准结果更为科学和准确。

1 数据说明及探索性分析

国控点“两尘四气”检测数据如表1所示。

表1 国控点“两尘四气”检测数据

表1显示了某国控点每小时“两尘四气”浓度的检测数据，共有4 200组，检测时间从2018年11月14日上午10：00到2019年6月11日下午15：00，共经历209 d零5 h，即5 021 h。

自建点“两尘四气”及5个气象指数检测数据如表2所示。

表2 自建点“两尘四气”及5个气象指数检测数据

表2是该国控点附近的1个自建点处“两尘四气”浓度和风速、压强、降水量、温度、湿度5个气象参数的检测数据，对应于国控点时间且2组数据间隔在5 min以内，共计234 717组数据[2]。

对实际检测数据进行探索性分析，包括以下4项内容：

(1)数据预处理。查找缺失数据、重复数据、无效数据，进行适当补充或者删除后得到有效数据。例如，国控点数据检测每小时记录1次，检测时间共计5 021 h，但表1中只有4 200 h的数据，共有821 h的数据缺失。假设不考虑天气突变因素，可以取缺失处前后邻近数据的平均值作为缺失处的补充。再如，自建点2019年5月21日3:59时刻的数据重复了138次，应删除掉。经过数据预处理，最终国控点补齐了5 021 h的数据，自建点保留230 152组有效数据。

(2)数据时间匹配设置。国控点只有每小时的数据，而自建点间隔5 min就有1组数据，为了与国控点数据相匹配，将自建点数据在对应小时上，选取前后半个小时的分钟数据进行加权平均(越接近小时权重系数越大)，从而得到自建点对应国控点的小时数据。

(3)差异性分析。对比国控点和自建点的小时数据，对两者的差异进行分析。计算国控点与自建点“两尘四气”数据的变异系数[3]，结果如表3所示。

表3 国控点与自建点“两尘四气”检测数据的变异系数对比

从表3的相对误差可以看出，相比国控点，自建点数据有一定误差，特别是NO2，SO2和O3。此外，以PM2.5为例，绘制国控点与自建点部分数据折线图，以进行直观对比。具体如图1所示。

图1 国控点与自建点PM2.5部分数据折线图

图1显示了国控点和自建点数据的差异，在同一时间自建点的数值普遍高于国控点。由此说明，自建点数据确实需要校准才能在实践中应用。

(4)相关性分析。对国控点“两尘四气”6个指标进行相关性分析，按照式(1)可计算任意2个指标之间的相关系数。

(1)

式(1)中，n为数据量；xi，yi为对应变量x和y的第i个观测值；x和¯y为变量x和y观测值的平均值。实际计算中可以借助软件完成[4]。结果表明：所有变量之间都存在相关关系，且PM2.5与PM10高度相关。同样，对自建点“两尘四气”6个指标和5个气象参数计算相关系数，也得到类似的结论。这说明空气质量指标数据之间会相互影响，特别是PM2.5与PM10之间有较大的依赖关系。

2 自建点数据校准的一元线性回归模型

以PM2.5为例(其余类似)，首先建立简单的一元线性回归模型对自建点数据进行校准。设PM2.5jz为自建点PM2.5的校准值，PM2.5zjd为自建点PM2.5的原始值，PM2.5gkd为对应时间国控点PM2.5的值。假设先不考虑其他空气指标的影响，PM2.5jz仅线性依赖于PM2.5zjd的值，即

PM2.5jz=β0+β1PM2.5zjd

(2)

式(2)中，β0和β1是未知的回归系数，由于校准值应该尽可能接近国控点数值，即

PM2.5gkd=PM2.5jz+ε

(3)

式(3)中，ε表示模型误差，一般服从正态分布。综合式(2)和式(3)，自建点的一元线性回归校准模型如下：

PM2.5gkd=β0+β1PM2.5zjd+ε

(4)

式(4)中，国控点和自建点的数据都是已知的，需要求出2个回归系数β0，β1，利用最小二乘法的原理(最小化误差的平方和)可以求出这2个系数，实际计算时通常借助数学软件来求解，比如通过MATLAB软件中的回归命令regress，即可求出回归系数[5]，在数据选取方面，取前4 021 h数据作为模型训练，留最后1 000 h数据作预测检验。模型计算结果如下：

PM2.5gkd=-0.012+0.802PM2.5zjd+ε

(5)

通过软件计算来做回归检验，回归的R值约为0.942，数值接近1代表回归模型成立。除PM2.5以外，其余5个空气指标(PM10，CO，NO2，SO2，O3)可做类似地校准处理。6个空气指标一元线性回归模型的平均绝对误差值(MAE)如表4所示。

表4 一元线性回归模型的平均绝对误差值(MAE)

表4中，原始误差1和训练值误差针对检测的前4 021 h数据，原始误差2和预测值误差则是检测的后1 000 h数据。原始误差是自建点原始数据与国控点数据的平均绝对误差，训练值误差和预测值误差则是自建点校准之后的数据与国控点数据的平均绝对误差。通过数值对比容易发现，训练值误差均小于原始误差，说明按照模型对自建点数据做校准有一定的效果。从预测值误差来看，PM2.5、PM10、CO浓度、NO2浓度的预测值优于原始数据，SO2浓度、O3浓度的预测值比原始数据差，一方面说明模型有待改进，另一方面，从微型检测仪自身的角度，也许仪器对SO2和O3的敏感性较差，检测结果不准导致校准有难度。

3 自建点数据校准的多元回归模型

在数据相关性分析中得出“两尘四气”6个指标之间存在相关性，如国控点PM2.5与PM10的相关系数为0.89，自建点二者的相关系数高达0.96。此外，自建点PM2.5与5个气象参数(温度、风速、湿度、气压、降水)之间也有相关性。因此，只用简单的一元线性回归模型来做数据校准过于粗糙，应建立多元回归模型。仍然以PM2.5为例(其余类似)，基于自建点的“两尘四气”6个指标和5个气象参数共11个指标，建立多元回归模型：

PM2.5jz=β0+β1PM2.5zjd+β2PM10zjd+

...+β11Humidity

(6)

由于校准值应该尽可能接近国控点数值，即

PM2.5gkd=PM2.5jz+ε

(7)

综合式(6)和式(7)，可得自建点的多元回归校准模型如下：

PM2.5gkd=β0+β1PM2.5zjd+β2PM10zjd+

...+β11Humidity+ε

(8)

式(8)中，国控点和自建点的数据都是已知的，需要求出12个回归系数β0,β1，…,β11，在计算中，先用全部变量作回归分析，并作系数、方程的检验，再作逐步回归，去掉系数无法通过检验的变量。借助软件计算，PM2.5的校准模型结果如下：

PM2.5gkd=0.195PM2.5zjd+0.441PM10zjd+

6.350x(COzjd)+0.147x(NO2zjd)+

0.046x(O3zjd)-1.526Wind+

0.003Pressure-0.028Rain+

0.178Tem-0.285Humidity+

ε

(9)

式(9)中，x(COzjd)为自建点CO浓度；x(NO2zjd)为自建点NO2浓度；x(O3zjd)为自建点O3浓度；Wind为风速；Pressure为压强；Rain为降水量；Tem为温度；Humidty为湿度。式(9)中去掉了1项SO2，它的系数检验未通过。其余5个空气指标[PM10，x(CO)，x(NO2)，x(SO2)，x(O3)]可做类似校准处理。同样计算6个指标的平均绝对误差值，如表5所示。

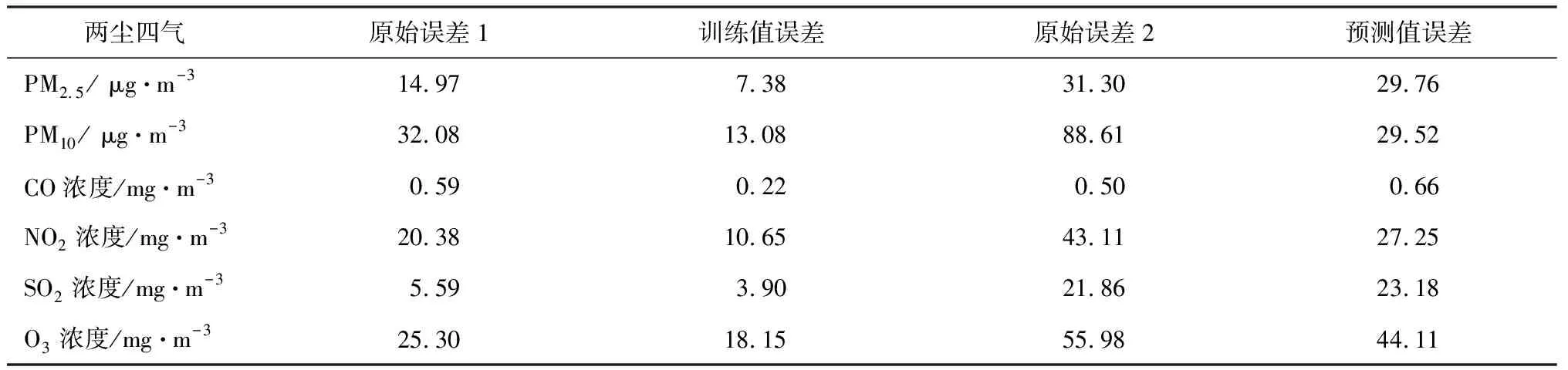
表5 多元回归模型的平均绝对误差值(MAE)

与表4相比，6个指标的训练值误差更小，预测值PM2.5，CO，SO2反而变差。从机理分析来看，多元回归模型更为合理，从数值结果来看，多元回归整体优于一元回归，个别项误差变大，但并不能说明模型不好，也许是数据本身的误差导致。

4 结论

本文对某公司研发的微型空气质量检测仪检测到的“两尘四气”数据进行了分析和校准研究，希望校准结果接近国控点检测数据。首先对原始数据进行了探索性分析，包括数据预处理、数据匹配、数据差异性分析、相关性分析等；其次分别建立了一元线性回归模型和多元回归模型对自建点数据进行校准，并对模型做了检验和误差分析。结果表明：多元回归模型的校准效果整体更优。然而，由于原始数据存在仪器误差、测量误差、气象因素误差等，导致校准精度不是特别高，后续工作应基于数据修正和模型改进来展开。