自适应精英变异粒子群算法在风电场无功优化中的应用
2022-01-25蒋慧
蒋 慧
(淮南联合大学 智能制造学院,安徽 淮南 232038)
风电场的功率输出受风速影响,易引起风电场节点的电压波动。基于双馈异步发电机的风电场作为无功源参与无功优化已经成为一种共识[1-3]。对风电场无功优化问题的研究取得了大量的成果。一些研究成果是在改进优化策略和模型基础上,将各种遗传算法、人工蜂群算法、粒子群算法等应用到无功优化模型的求解中[4-9]。
粒子群优化算法因其良好的优化性能和通用性被广泛应用于复杂函数优化、电力系统等领域[10-11],但是,传统PSO算法对算法参数依赖大,且易出现早熟,所以,一些研究成果从动态调整参数、改进粒子速度和位置更新公式、采用混合智能算法等对PSO算法做了大量的改进和优化,以提高算法的搜索能力和收敛精度[12-17]。文献[14-17]均采用了精英变异策略对粒子群算法进行了改进和优化。
基于上述分析和总结,在基本粒子群的基础上,根据迭代过程中的适应度函数值的收敛程度非线性动态调整惯性权重值,并将全局最优视为精英粒子进行变异,得到一种自适应精英变异粒子群算法。基于含风电场的多目标无功优化模型进行归一化处理并采用层次分析法确定各优化目标权重构建目标函数,以该目标函数作为自适应精英变异粒子群算法的自适应度函数进行求解。
1 自适应精英变异策略粒子群算法
本算法的主要优化思路是在标准粒子群算法的基础上,在每一次迭代前根据上一次迭代产生的全局最优值改变算法的惯性权重值,达到高效搜索、加速收敛。同时为了避免出现早熟,引入精英变异策略。
1.1 标准粒子群算法
标准粒子群算法是一种随机搜索优化算法,其优化流程是设定粒子种群规模并随机初始化,通过自适应值来评价粒子个体优劣并进行不断地迭代,更新粒子的速度和位置,直到达到收敛精度,迭代进化公式如式(1)[18]所示。
(1)
式中:t为迭代次数;Vi和Xi为第i个粒子的速度和位置矢量;pbesti和gbest为个体最优值与全局最优值;ω为惯性权重;c1和c2为学习因子;r1和r2为[0,1]的随机数。
1.2 自适应动态惯性权重
当各个粒子的惯性权重随着迭代次数的增加而简单的线性或者非线性递减时会降低搜索精度,所以在递减的基础上,考虑惯性权重值根据粒子的位置而产生的动态变化,即在粒子迭代进化过程中,当粒子的适应度值大于平均值时直接取最大惯性权重值,增大搜索速度;当粒子的适应度值小于平均值时,将个体粒子距最优值的距离与群体所有粒子距最优值平均距离的比值作为非线性系数进行自适应动态调整。非线性自适应动态调整的惯性权重值确定如公式(2)[18]。
(2)
式中:fi为第i个粒子的适应度值;fmin和favg分别为当前迭代次数下的粒子适应度最小值和平均值;ωmax和ωmin分别为惯性权重的最大值和最小值。
1.3 精英变异策略
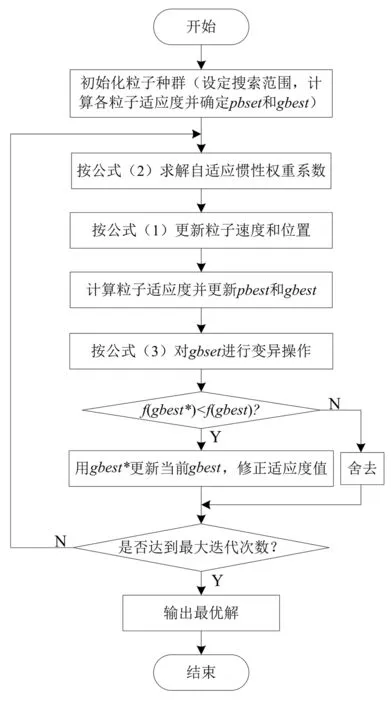
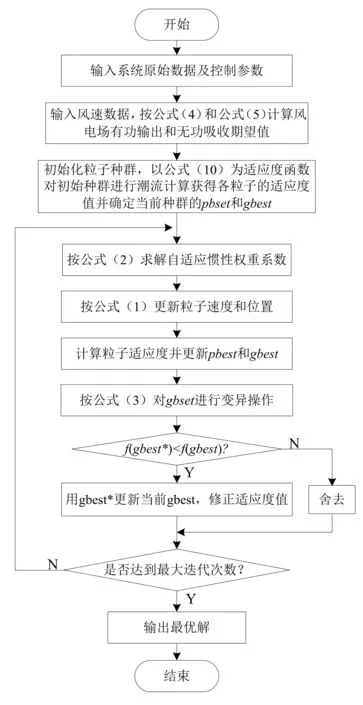
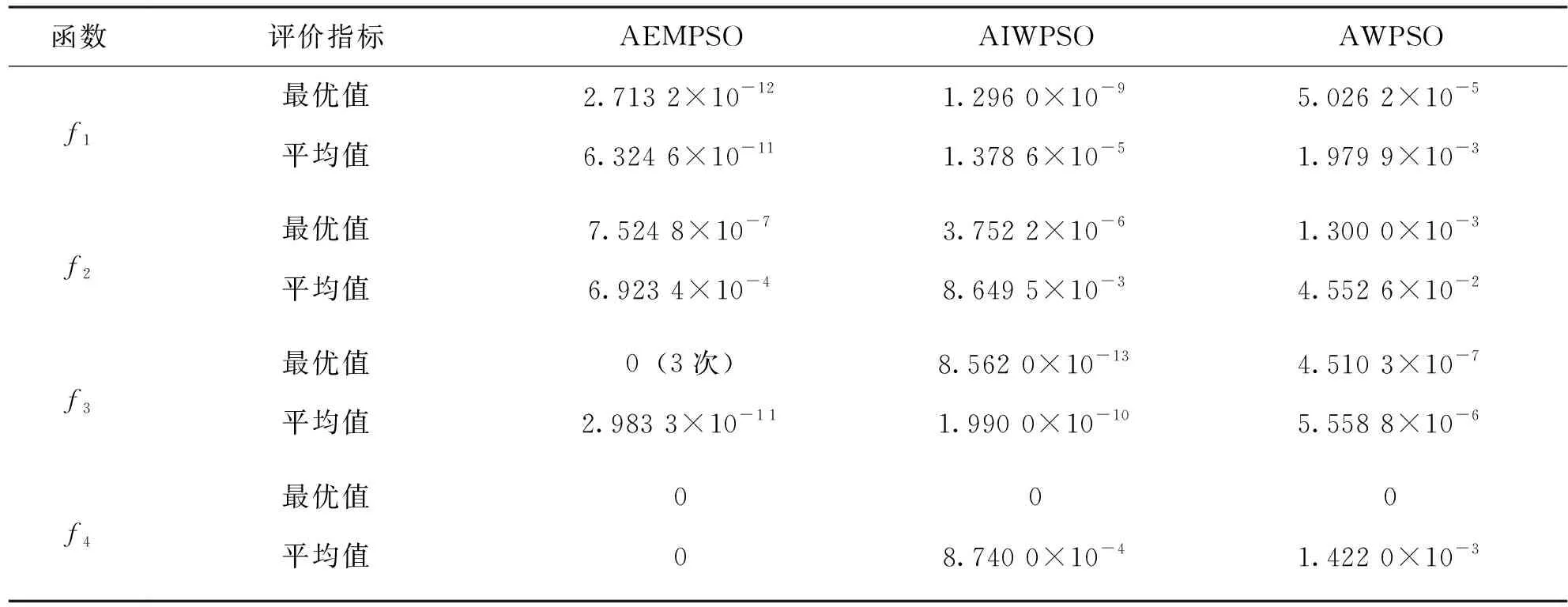
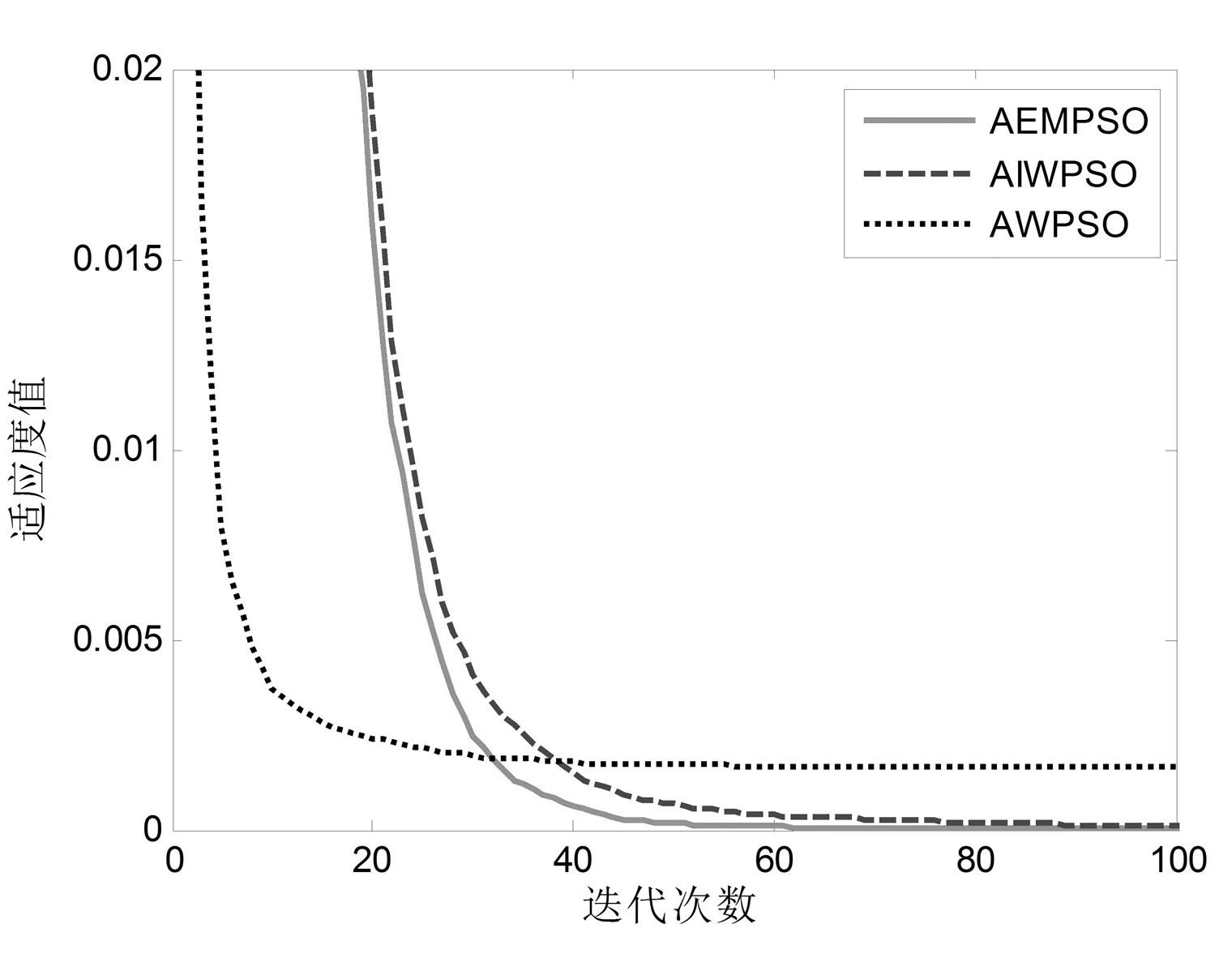
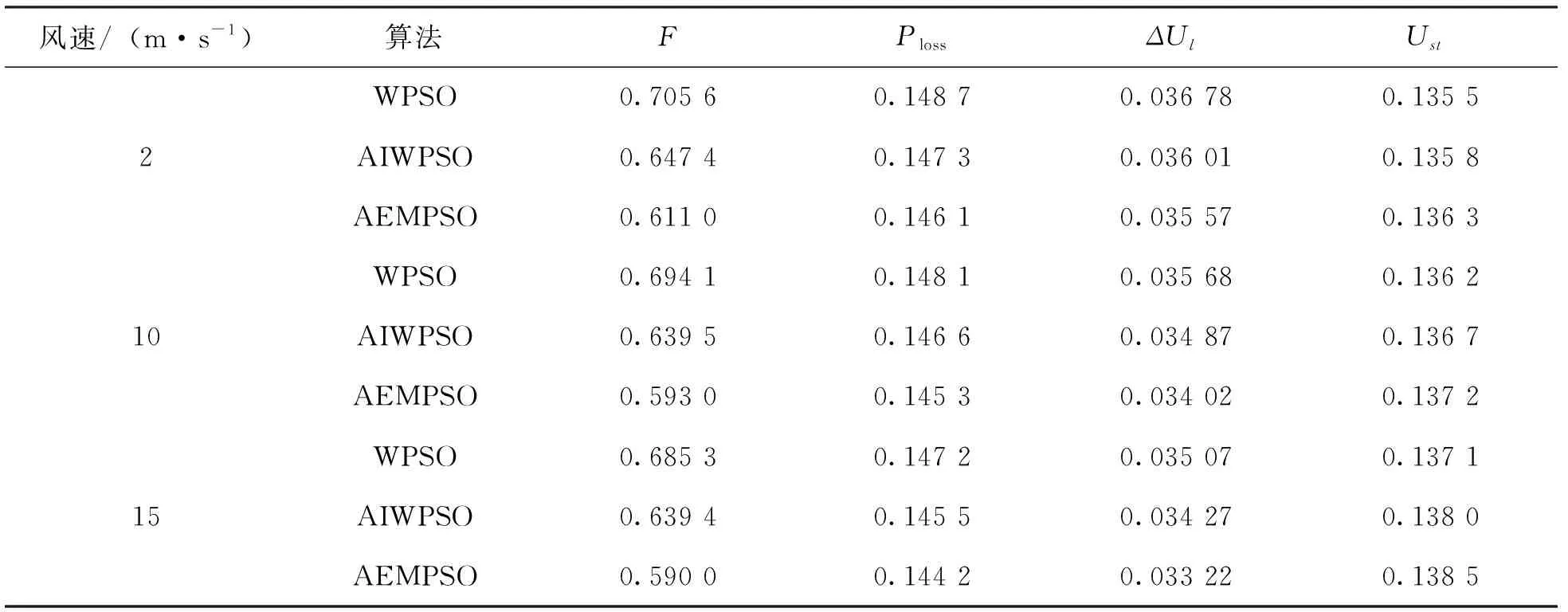
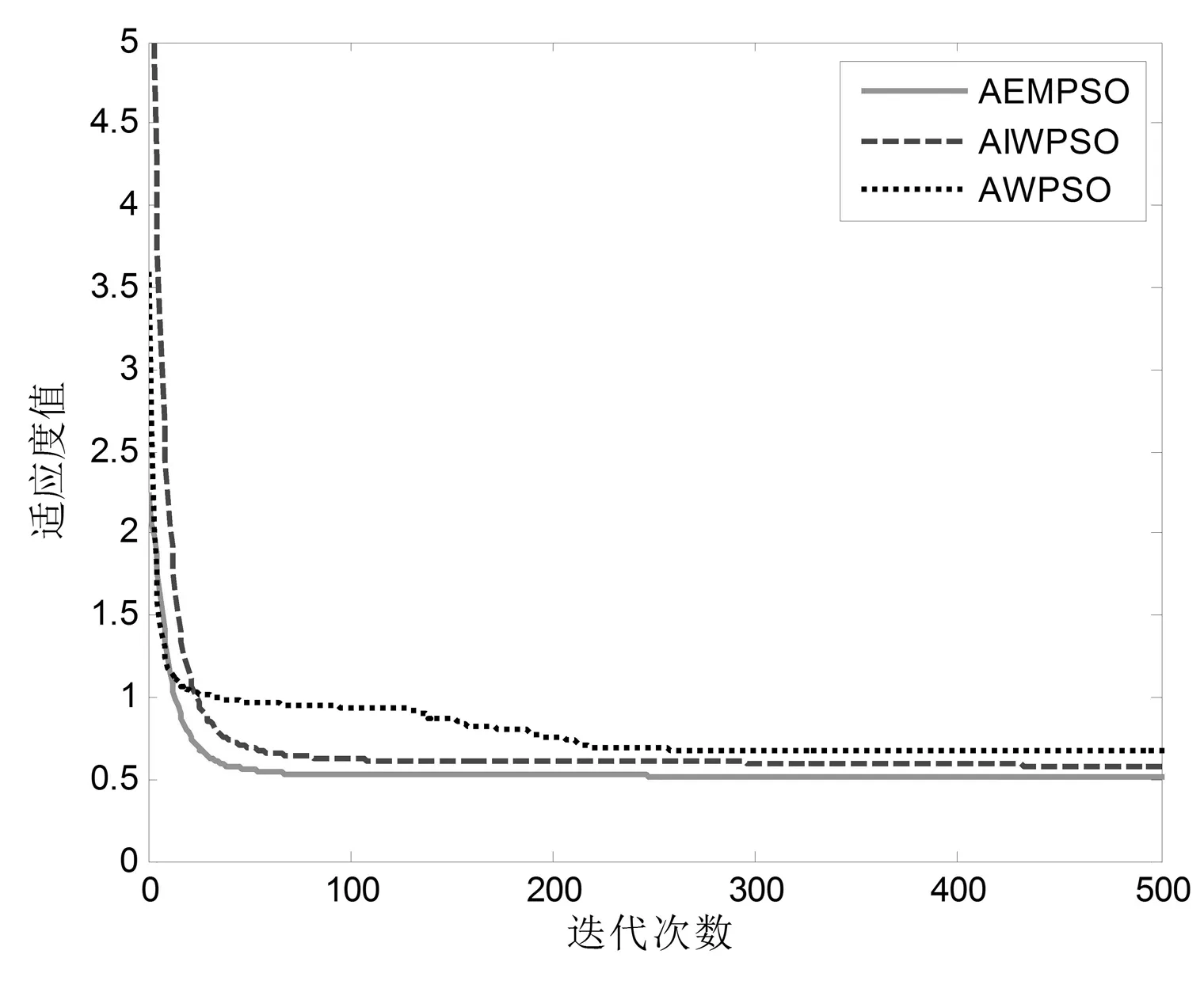
为了降低算法陷入局部最优的可能性,在每次迭代进化过程中,将全局最优值gbest作为种群的精英粒子,然后对gbest增加一个随机扰动而变异形成新的粒子gbest*,比较适应度值f(gbest*)与f(gbest),如果f(gbest*) (3) 式中:tmax为最大迭代次数;favg-fpg为当前各粒子与全局最优的平均距离;μ为满足标准柯西分布的随机数;k1、k2和k3为常数,其中k1和k2用于控制扰动变量范围,k3用于控制扰动因子的调节能力。 综上所述,自适应精英变异粒子群算法的具体流程如图1所示。 图1 自适应精英变异粒子群算法流程图 为了简化计算,风力发电机在不同风速下有功出力采用近似功率曲线直接转换风速值的方法进行计算,近似计算模型如下: (4) (5) 图2 异步风力发电机Γ型等效电路 式中:QG为风力发电机吸收的无功功率,PG为风力发电机有功输出。 综上所述,风电场的总有功出力和吸收的总无功功率分别采用式(4)和式(5)计算并求和。 建立以有功网损Ploss最小、负荷节点电压偏移量ΔUl最小以及静态电压稳定裕度Ust最大为多目标的含风电场无功优化目标函数如下[5]: (6) 式中:Gl(i,j)为第l条支路的导纳;Ui、Uj、δij分别为节点i,j的电压和相角;Uk、UkN、ΔUkmax分别为负荷节点的电压实际值、期望值和最大允许偏差;λmin为潮流雅可比矩阵最小奇异值。 潮流等式约束如公式(7)所示: (7) 式中:PGi、QGi、PLi、QLi和ΔQC分别是节点i的有功出力、无功出力、有功负荷功率、无功负荷功率和无功补偿功率;Gij和Bij分别是节点导纳矩阵第i行第j列元素的实部和虚部;Nnode节点数。 不等式约束如公式(8)所示[8]: (8) 式中:Qh和Ui为状态变量,分别是发电机的无功出力和节点电压;Tk和Cr为控制变量,分别是变压器变比和电容器投切容量。在潮流计算时可将风电场视为PQ节点,潮流计算时修改风电场节点对应的雅可比矩阵对角线元素[19]。 式(6)的多目标优化函数存在量纲不同、有最小和最大不同优化值的优化方向以及3个子目标的重要程度不同的问题,需要进行归一化处理同时设置相应的权重。 进行线性归一化处理到[0-1]如式(9)所示。 (9) (10) 式中,λ1、λ2、λ3为各优化目标的权重系数。 满足电压偏移在约束范围内,多考虑经济性和静态电压稳定性。优化指标中有功损耗和电压稳定裕度比电压偏移量稍微重要,权重系数按层次分析法构造判别矩阵为: (11) 计算得出权重向量为: (12) 综上所述,基于上述风电场的功率和潮流计算,将归一化后的无功优化目标函数作为精英变异粒子群算法的适应度函数进行求解,具体流程如图3所示。 图3 基于AEMPSO算法的无功优化求解流程图 为了测试和比较本算法(AEMPSO)的性能,一种结合惯性权重自适应非线性递减和粒子随机变异的改进粒子群算法(AIWPSO)[20]和自适应惯性权重粒子群算法(AWPSO)[18]对表1的4个标准测试函数(极值均为0)进行最值求解,设定3个算法粒子个数N=50、ωmax=0.9、ωmin=0.4、tmax=1 000,取各运行50次的最优值并计算平均值如表2所示,绘制适应度平均收敛曲线如图4所示。 表1 测试函数 表2 测试函数适应度收敛值比较 (a) Sphere函数 由表2的3个算法对4个标准函数求解的最优值和平均值可知,无论是单峰函数还是多峰函数,Aempso算法的收敛精度均优于对比算法。 由图3的50次平均收敛曲线可知,Awpso算法基本上在迭代50次以内就接近其最优值而出现早熟现象,Aempso算法较Aiwpso算法收敛速度较快。对4个测试函数分别设置相应的允许误差,则4种算法收敛到理论值的概率如表3所示。 表3 算法稳定性比较 综合表2和表3可知,在相应的允许误差下,本文的Aempso算法稳定性优于对比算法。 将IEEE14节点标准测试系统节点3的常规电厂更改为一个总装容量为12 MW(20×600 kW)的风电场,如图5所示。机端电压为0.69 kV,经变压器将风电场并入110 kV系统,设切入风速vin=3 m/s,切出风速为vout=20 m/s,额定风速为vN=12 m/s,采用标幺值计算且基准值均取100 MVA,风力发电机其他参数如表4所示。设定3个算法粒子个数N=50、ωmax=0.9、ωmin=0.4、tmax=1000。 图5 含风电场的IEEE14节点电力系统 表4 风力发电机技术参数(单位:pu) 当风速为12~20 m/s之间时,风力发电机恒功率输出,此时风电场输出功率为定值。所以,取15 m/s作为恒功率状态风速值,同时取风速为2 m/s(停机状态)和10 m/s(最大风能跟踪状态)3个状态下进行粒子群优化算法对无功优化目标函数的优化结果及优化后Ploss、ΔUl和Ust的标幺值(单位:pu)如表5所示。 表5 不同风速下的无功优化结果 由表5所示的优化结果可知,随着风速的增加风电场有功出力增加,系统的有功网损和电压偏差均减小,静态电压稳定裕度增大。主要因为风电场有功出力的增加减小了有功功率向风电场节点的流动量。 取15 m/s风速下的初始潮流计算(优化前)的Ploss、ΔUl和Ust标幺值分别为0.156、0.042 3、0.130 7,通过对比表5可知,各优化算法均具有良好的优化效果。进一步分析表5所示的各算法的优化结果可知,在相同的风电场有功出力下,自适应精英变异粒子群算法的优化效果优于对比算法。 绘制15 m/s风速下目标函数优化平均收敛曲线如图6所示。由图6可知,自适应精英变异粒子群算法对本无功优化目标函数求解的收敛速度和精度均优于对比算法。 图6 15 m/s风速下目标函数平均收敛曲线 提出了一种自适应精英变异粒子群算法,通过标准测试函数验证,克服了早熟现象且收敛精度高、稳定性好。基于多目标无功优化模型进行了归一化处理并采用层次分析法确定各优化目标权重构建了目标函数,将自适应精英变异粒子群算法用于求解含风电场多目标无功优化目标函数,通过对含风电场IEEE14测试系统无功优化的仿真实验表明,对含风电场的电力系统多目标无功优化具有良好的无功优化效果。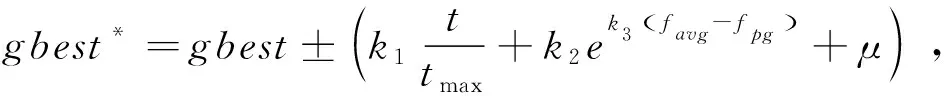
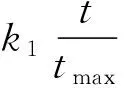
2 含风电场电力系统无功优化目标函数
2.1 异步风力发电机数学模型
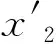
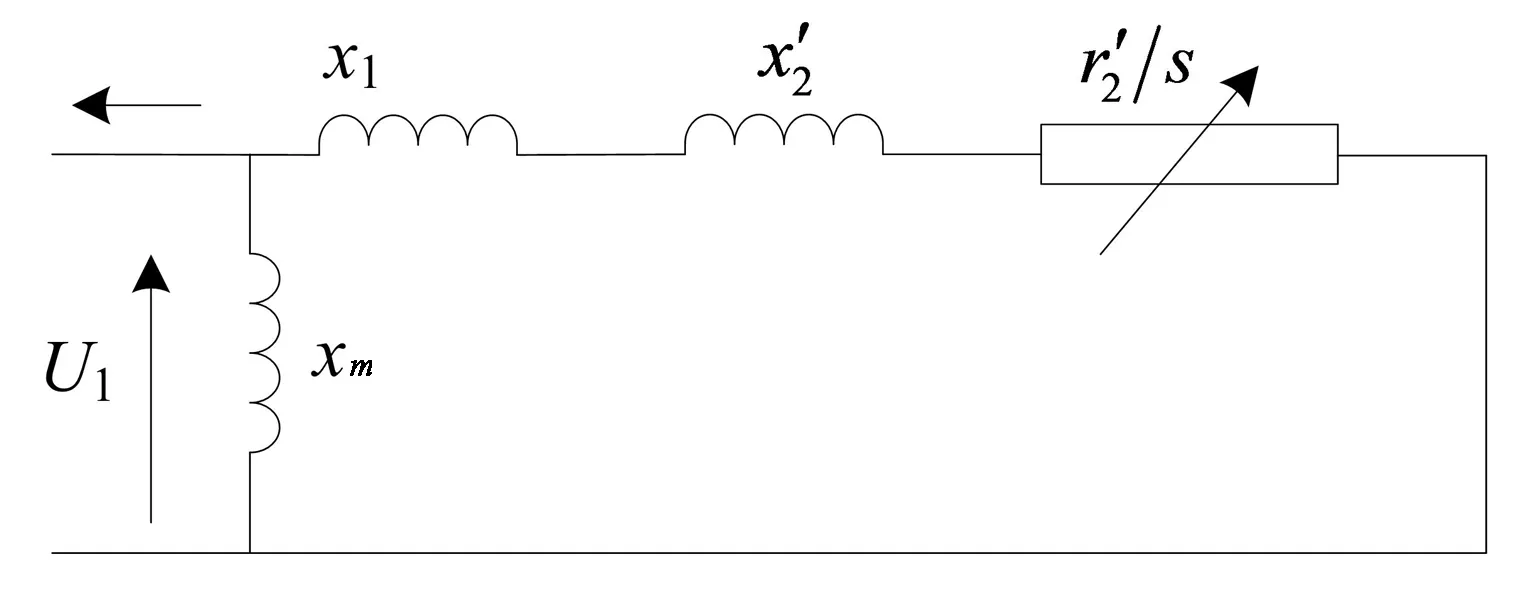
2.2 无功优化目标函数及约束条件
2.3 目标函数归一化处理
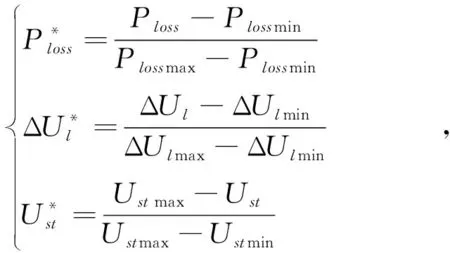
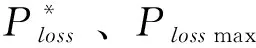
3 仿真结果与分析
3.1 标准函数测试与分析


3.2 IEEE14测试系统验证


4 结语
