一种适用于图像信号的压缩感知测量矩阵
2022-01-25李文宗华钢
李文宗, 华钢
(中国矿业大学 信息与控制工程学院, 江苏 徐州 221116)
0 引言
目前无线传感器网络(Wireless Sensor Network, WSN)广泛用于煤矿井下数据传输。矿井无人工作区监控图像信息量较大,在图像的传输、存储阶段对硬件性能要求较高,造成传感器节点耗能增大、寿命骤减等问题[1]。数据压缩是解决上述问题的有效方法之一。压缩感知(Compressive Sensing, CS)[2]作为一种编码简单、译码复杂的高效数据压缩方法,编码端可以远小于奈奎斯特采样频率采集信号并进行信号压缩,解码端通过适合的恢复算法重建信号,解决了网络中数据量急增、能量消耗快等问题,特别适用于WSN中视频传感器节点端对端的图像信号传输场景[3]。
目前,CS的研究主要集中在信号获取与重建2个部分,它们都与测量矩阵有着密切联系。一个设计得当的测量矩阵能够以较少的测量数目获得信号的完整信息。目前测量矩阵主要分为随机性测量矩阵和确定性测量矩阵2类[4]。Gause测量矩阵[5]是一种较有代表性的随机测量矩阵,矩阵元素随机性较强,可在高概率上服从约束等距条件(Restricted Isometry Property, RIP)。文献[6]设计了一种随机的稀疏矩阵,矩阵元素大部分为零,易于存储,然而该矩阵的RIP特性有待验证。文献[7]提出了一种改进Gause随机测量矩阵,压缩性能较好,但仍需较大存储空间。随机测量矩阵虽然性能较好,但在应用时需要被传输、硬件不易实现,且无法保证每一次生成的测量矩阵的性能。基于此,学者们提出了诸多构造确定性测量矩阵的方法。文献[8]利用信号匹配原理提出了一种适用于超宽带(Ultra Wide Band, UWB)系统的测量矩阵,信号重建性能较好,但适用性不够广泛。文献[9]结合双极性混沌序列与托普利兹矩阵,提出了一种块状的感知矩阵,比随机测量矩阵易于实现,但信号重建精度的提高有限。文献[10]引入分类圆理论,提出了一类卷积压缩感知测量矩阵,矩阵的相关性较小,但构建过程略为复杂。文献[11]引入GMW序列构造了一种确定性的测量矩阵,该矩阵易于构建,但矩阵元素仍具有一定的随机性。文献[12]利用Bose平衡不完全区组构造了一类性能优异的测量矩阵,对一维随机信号重建效果较好,但对煤矿监控信号重建性能不够理想。文献[13]提出了一种基于Kasami码的确定性测量矩阵,矩阵列正交性较强,但对图像信号重建精度有待提高。上述确定性测量矩阵的维度相对固定,通常对一维信号的重建性能较好,但对矿井监控图像信号的重建性能不理想,精度较低。
针对上述问题,本文以矿井WSN为背景,利用时域非均匀采样与分块思想,将多个相同的小尺寸帕斯卡矩阵以对角线方式排列,构建了一种新的基于帕斯卡矩阵的块状压缩感知测量(Block Pascal Compressive Sensing Measurement, BPCSM)矩阵,同时结合联合正交匹配追踪算法实现了矿井监控图像信号的压缩采样与重建。BPCSM矩阵为确定性测量矩阵,构造简单,存储空间较少,易于实现。实验结果表明,对于矿井监控图像,与常用的测量矩阵相比,该测量矩阵具有较高的重建精度,满足矿井环境应用要求。
1 基本理论
1.1 压缩感知
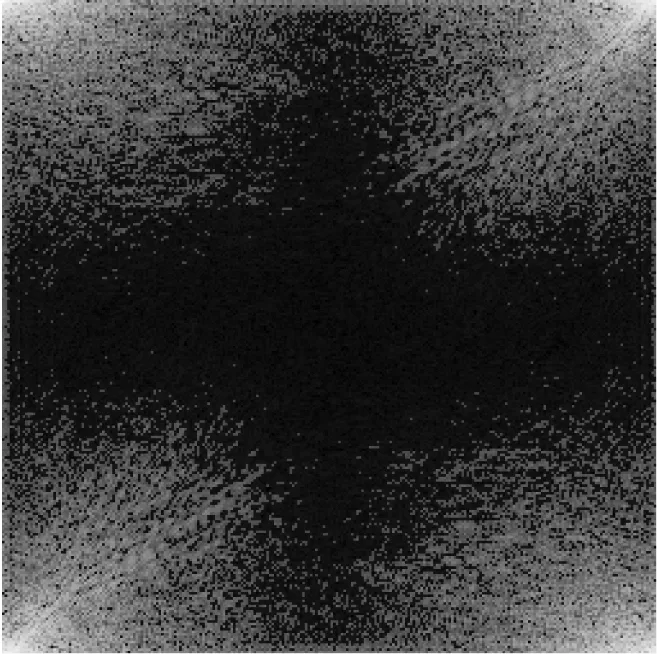
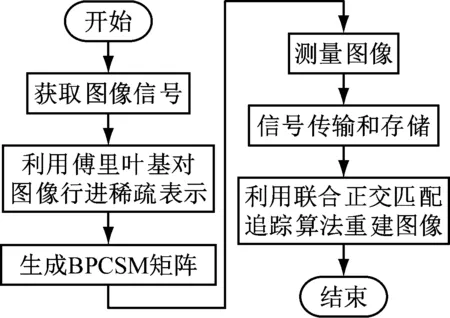
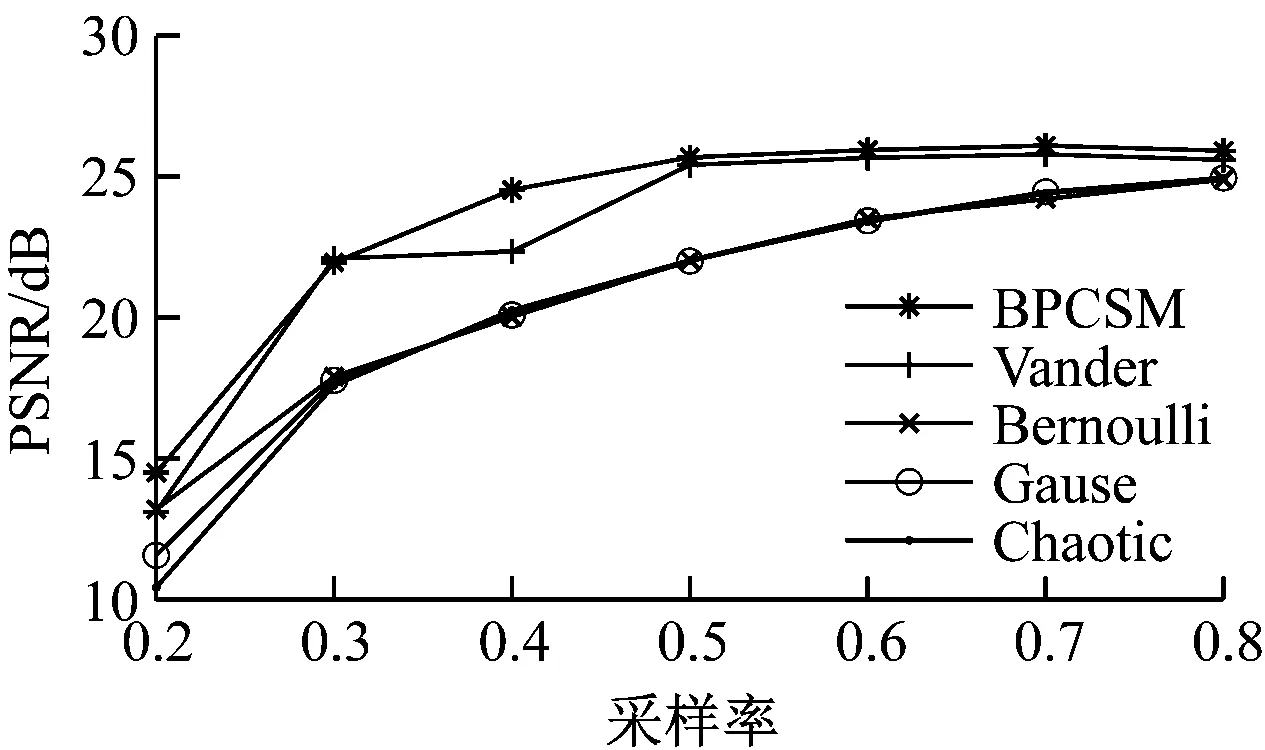
对一个N维信号x,x∈RN(R为实数集),若x含有K个非零元素,则称x为K稀疏信号。通过测量矩阵Φ对稀疏信号x线性投影,能够获得M维信号y,y∈RM,且满足M y=Φx (1) 自然界中的大部分信号本身并不稀疏,但可以在某一个域中进行稀疏表示,即有x=Ψs,其中Ψ为N×N维稀疏基,s为N维稀疏信号。于是式(1)可整理为 y=Φx=ΦΨs=As (2) 式中A为感知矩阵。 式(2)即为CS信号获得的过程。由y重建x理论上有无穷多的解。但CS理论指出,若Φ选取恰当,压缩后信号y便能包含重建原信号x所需的足够多信息,重建问题即可转化为最小l0范数的求解问题。 (3) 然而式(3)的求解是一个非确定性多项式难题。文献[14]证明可以通过l1范数问题代替求解。 (4) 为评价不同测量矩阵性能,J.C.Emmanuel[15]提出了RIP。对任意的稀疏信号x,如果存在最小的约束等距常数δk,并满足式(5),那么认为测量矩阵Φ满足RIP。其中k为x中非零元素个数,0<δk<1。当δk足够小时,式(3)的求解可通过贪婪算法或凸优化算法较好解决[11]。 (5) 一般地,直接验证一个测量矩阵的RIP是极为困难的。于是B.Jean等[16]提出了相干系数μ(Φ)的概念,为评价测量矩阵性能提供了更为简单的方法。测量矩阵的相干系数是指任意2个列向量φj1,φj2(j1,j2表示列向量索引)归一化内积绝对值的最大值,数学形式为 (6) 文献[16]证明μ(Φ)与RIP条件满足如下关系: δk≤(k-1)μ(Φ) (7) 由式(7)可知,当相干系数足够小时,测量矩阵很容易满足RIP。因此,可通过降低相干系数,保证测量矩阵良好的重建性能。 BPCSM矩阵的构建首先需选定帕斯卡矩阵为基矩阵,然后依据采样率确定帕斯卡矩阵的尺寸,最后将帕斯卡矩阵以对角线方式串联排列,实现对图像信号的压缩采样和重建。 帕斯卡矩阵是一种对称正定矩阵,矩阵元素满足帕斯卡三角形规律[17]。4×4阶帕斯卡矩阵为 (8) 帕斯卡矩阵满足以下特点: (1) 矩阵的第1行、第1列元素均为1。 (2) 当行索引i>1、列索引j>1时矩阵元素满足递推关系。 ai,j=ai,j-1+ai-1,j (9) 式中ai,j为矩阵第i行第j列的元素。 (3) 矩阵行向量或列向量线性无关。 (4) 当i>1时,满足ai,j 通常图像信号的行维数与列维数较高。若直接将帕斯卡矩阵作为测量矩阵,矩阵元素会随着行数、列数的增加急剧增大,非常不利于测量矩阵的实现和存储。基于文献[18],本文选用分块操作方式,将帕斯卡矩阵当作测量矩阵的子块(基矩阵),并按对角线排列为维度较高的测量矩阵。由帕斯卡矩阵构建M×N维BPCSM矩阵的具体步骤如下: (1) 给定待采样信号维度N、采样率r,根据N和r计算出M,M=Nr。 (3) 构建n×n维帕斯卡矩阵,取前m行构建m×n维基矩阵P。 (5) 生成mL×nL维矩阵,选择后M行、后N列,构建M×N维BPCSM矩阵ΦP。 (10) 由以上步骤可知,分块操作使BPCSM矩阵大部分元素为0,同时基矩阵P元素均为整数,便于硬件实现;BPCSM矩阵的构建仅需乘幂和复制操作,构建时间短,相较于稠密矩阵,能够降低信号采样的计算复杂度,对高维信号的采样有更好的适应性;基矩阵列向量线性无关,且全部位于主对角线上,使得BPCSM矩阵列向量间的相关性较小;不同分块列向量间非零元素位置互不重叠,采样信号段也不同,故能够实现并行采样,提高采样效率[18];对M×N维的BPCSM矩阵,只需存储基矩阵行数m便可以构建整个测量矩阵。 为进一步说明BPCSM矩阵在重建图像上的优势,绘制了矿工、Lena图像经傅里叶稀疏基变换后的能量图,如图1所示。 长时间TH过量,就会损伤胰岛素功能,如果胰岛素分泌降解加快且分泌量减少后,孕妇的糖尿病以及相关并发症就会加重,同样,糖尿病也会导致孕妇出现甲状腺等疾病。相关学者研究指出,对糖尿病患者做好饮食控制,在血糖稳定后,患者甲亢危象以及并发症就会消除[7]。当孕妇甲状腺功能出现异常时,会导致其血脂指标紊乱,低密度脂蛋白胆固醇以及载脂蛋白、甘油三酯水平上升。 (a) 矿工图像能量 (b) Lena图像能量 由图1可知,无论矿工图像还是Lena图像,经稀疏变换后其图像信号的能量大部分集中在系数矩阵的4个角上,即图中的高亮部分,这表明图像能量集中在低频区域。基矩阵主对角线排列的方式能够保证BPCSM矩阵左上角及右下角非零元素较为充足,与系数矩阵的结构对应性较好,利于图像低频系数的测量与恢复。同时基矩阵元素取值较大的特点,使得BPCSM矩阵具有较强的信息获取能力,从而能够提高图像整体的重建效果。 基于BPCSM矩阵的矿井监控图像信号的压缩采样、重建步骤如图2所示。 图2 基于BPCSM矩阵的矿井监控图像信号的 压缩采样、重建Fig.2 Compression sampling and reconstruction steps for mine monitoring images signals based on BPCSM matrix (1) 获取矿井监控图像信号,确定图像尺寸。 (2) 利用傅里叶函数生成傅里叶稀疏基[6],对步骤(1)所获取的图像信号进行稀疏表示。 (3) 设定采样率,确定基矩阵尺寸、分块数,以2.2节方法生成BPCSM矩阵。 (4) 应用BPCSM矩阵对步骤(2)中稀疏表示后的图像进行测量。 (5) 传输并存储步骤(4)中测量后的图像信号。 (6) 基于步骤(2)的傅里叶稀疏基、步骤(3)的BPCSM矩阵,利用联合正交匹配追踪算法[20]重建图像。 实验部分测试了BPCSM矩阵用于图像信号重建时的性能,并以矿井监控图像压缩感知中常用的Vander测量矩阵、Gause测量矩阵、Bernoulli测量矩阵、Chaotic测量矩阵作对比。数据源选取矿井中较有代表性的煤块图像、矿工图像、顶板支撑图像。为不失一般性,同样选取Lena图像、Barbara图像、Boat图像作测试。6张原始图像如图3所示,大小均为255×255。 (a) 矿工 (b) 顶板支撑 (c) 煤块 (d) Lena (e) Barbara (f) Boat (11) 由MSE获取PSNR的数学表达式为 (12) 在采样率为0.2~0.8的条件下,测试了不同测量矩阵对矿工、Lena图像的主观重建效果,分别如图4和图5所示。为减小随机性对高斯测量矩阵的影响,本文实验结果均为重复200次后所得平均值。 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 22.083 1 dB 25.999 0 dB 27.150 8 dB30.109 4 dB30.605 4 dB 30.650 0 dB30.492 4 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 16.947 9 dB26.376 1 dB25.261 5 dB29.780 2 dB30.313 9 dB30.355 1 dB30.225 9 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 15.623 8 dB 20.587 7 dB24.387 5 dB 26.008 7 dB 27.991 2 dB29.035 6 dB29.673 4 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 15.525 3 dB20.125 8 dB 23.804 5 dB26.165 5 dB27.898 4 dB29.014 0 dB 29.882 5 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 14.005 3 dB20.339 5 dB 24.701 6 dB25.979 2 dB27.941 4 dB29.324 2 dB 29.787 2 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 由图4可看出:当采样率为0.3时,由BPCSM矩阵、Vander测量矩阵重建的矿工图像的PSNR分别为25.999 0, 26.376 1 dB,图像相对清晰,仅存在少量条状伪影,而由Gause测量矩阵、Bernoulli测量矩阵、Chaotic测量矩阵重建的矿工图像的PSNR均小于20.59 dB,图像存在大量块状伪影,矿工面部细节较难辨别;当采样率为0.5时,BPCSM矩阵已几乎可以恢复矿工图像的全部细节。BPCSM矩阵的重建效果明显优于Gause测量矩阵、Bernoulli测量矩阵和Chaotic测量矩阵,与Vander测量矩阵相比重建性能也有一定的提高。 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 15.774 7 dB 20.296 8 dB21.368 6 dB 25.684 7 dB 26.136 0 dB26.336 3 dB26.199 1 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 12.707 3 dB20.361 3 dB19.888 7 dB25.344 2 dB25.828 7 dB26.022 0 dB25.892 8 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 11.496 8 dB15.992 2 dB19.182 1 dB21.934 4 dB23.543 2 dB24.667 2 dB25.287 4 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 12.988 9 dB15.798 9 dB19.341 7 dB21.766 3 dB23.556 3 dB24.592 5 dB25.326 5 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 原始图像 PSNR=PSNR= PSNR= PSNR= PSNR= PSNR= PSNR= 10.435 2 dB15.364 3 dB19.234 4 dB21.615 3 dB23.743 7 dB24.917 2 dB 25.213 5 dBr=0.2 r=0.3 r=0.4r=0.5 r=0.6 r=0.7 r=0.8 由图5可看出:BPCSM矩阵对Lena图像,即非矿井监控图像的重建效果同样较好。当采样率为0.3时,由BPCSM矩阵重建的Lena图像的PSNR为20.296 8 dB,图像仅存在较少块效应;当采样率为0.5时,BPCSM矩阵已经能够较好地重建Lena图像。通过对比发现,由Gause测量矩阵、Bernoulli测量矩阵和Chaotic测量矩阵重建的Lena图像模糊,损失了较多像素信息。5类测量矩阵在相同采样率下重建Lena图像的PSNR均低于重建矿工图像的PSNR,这是因为Lena图像的频率更为丰富,重建时需更多的图像细节。 为进一步对比BPCSM矩阵与其他测量矩阵的图像重建性能,计算了5类测量矩阵在采样率为0.2~0.8下重建顶板支撑、煤块、Barbara、Boat图像的PSNR,如图6所示。 (a) 顶板支撑 (b) 煤块 (c) Barbara (d) Boat 由图6可看出,随着采样率的增大,5类测量矩阵重建图像的PSNR总体上表现为增加趋势。Gause测量矩阵、Bernoulli测量矩阵、Chaotic测量矩阵在重建图像时呈现出相似性能,BPCSM矩阵在任一采样率下的重建性能都明显优于该3个矩阵。BPCSM矩阵在采样率为0.3时的重建性能与Vander测量矩阵相当,而在其他采样率下的重建性能优于Vander测量矩阵。当采样率大于或等于0.5时,5种测量矩阵的重建性能曲线是逐渐收敛的,并且BPCSM矩阵重建图像的PSNR随采样率的增加而缓慢增长甚至出现减小现象,当采样率小于0.5时其重建性能更为突出。 此外,考虑到基矩阵的大小对BPCSM矩阵重建性能可能产生影响,本文同样在采样率为0.5、不同基矩阵尺寸条件下对BPCSM矩阵的重建性能进行了测试,测试结果见表1。 表1 不同基矩阵尺寸下BPCSM矩阵重建 图像效果客观对比Table 1 Objective comparison of images reconstruction effects of BPCSM matrix under different base matrix sizes 由表1可看出,基矩阵尺寸越大,BPCSM矩阵的图像重建性能越差,这是由于BPCSM矩阵行向量间的正交性降低所导致。较小的基矩阵尺寸能够提高BPCSM矩阵的重建性能,并且方便硬件实现。然而当基矩阵尺寸减小至2×4时,其对图像信号的重建性能却劣于尺寸为3×6时的性能,这是因为基矩阵尺寸过小使得BPCSM矩阵零元素过多,导致矩阵获取信息的能力减弱。因此,在实际应用中,应该根据实际情况选择合适的基矩阵尺寸。 (1) 基于帕斯卡矩阵,提出了一种适用于矿井监控图像信号的压缩感知BPCSM矩阵。BPCSM矩阵基于分块操作方式,将多个相同的小尺寸帕斯卡矩阵以对角线方式排列,同时结合联合正交匹配追踪算法实现矿井监控图像信号的压缩采样与重建。BPCSM矩阵设计时加入的分块思想能够方便其在硬件上的实现,具有低存储、构建简单等特点。 (2) 实验结果表明:BPCSM矩阵对矿井监控图像信号的重建性能高于Vander、Gause等常用测量矩阵,当采样率为0.3时,基于BPCSM矩阵重建的矿工图像的PSNR约为26 dB,矿工面部轮廓较为清晰;当采样率为0.5时,基于BPCSM矩阵重建的矿工图像的PSNR达到了30 dB,几乎可以恢复矿工图像的全部细节,表明BPCSM矩阵具有较优的重建质量。BPCSM矩阵对非矿井监控图像的重建效果同样较好。 (3) 不同的基矩阵尺寸对BPCSM矩阵的图像重建性能存在一定的影响,选取合适的基矩阵尺寸能够提高BPCSM矩阵的图像重建精度。 (4) 下一步工作将深入分析帕斯卡矩阵的结构特点,进一步提高BPCSM矩阵在高采样率下的重建性能。1.2 约束等距条件与相干系数

2 BPCSM矩阵构建
2.1 帕斯卡矩阵
2.2 BPCSM矩阵构建步骤及性能分析

3 基于BPCSM矩阵的图像重建
4 实验与分析






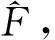










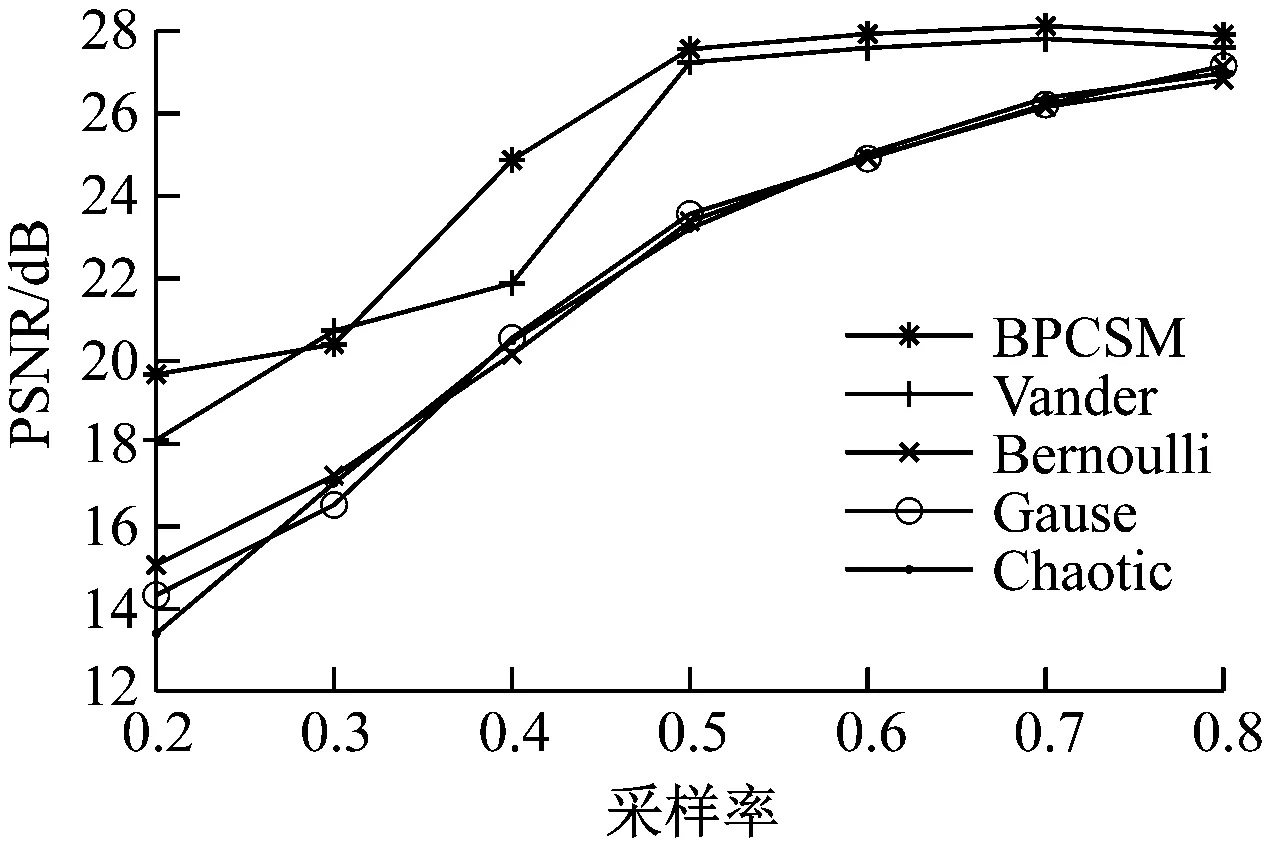
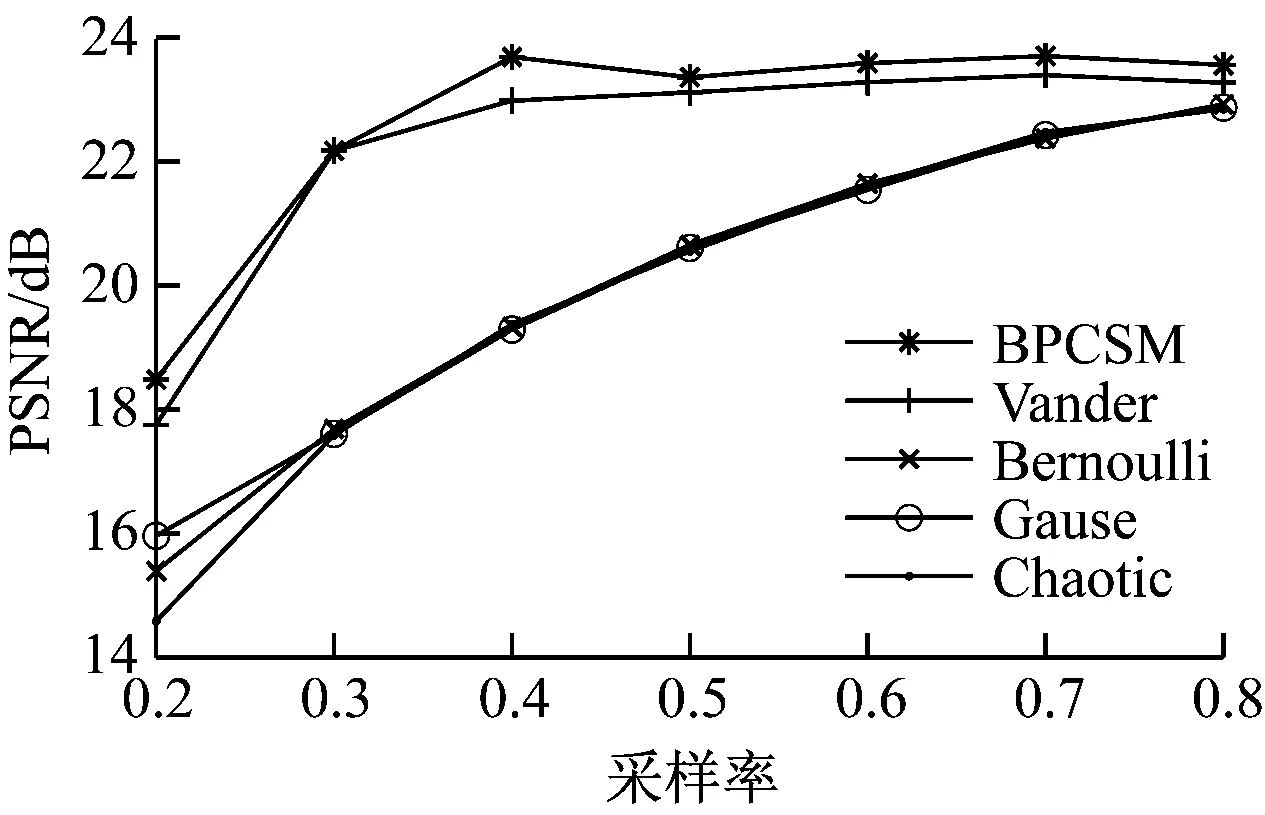

5 结论
