基于LQR的车道保持辅助控制策略

张义奇，牛礼民，朱奋田

(安徽工业大学机械工程学院，安徽 马鞍山 243032)

随着科技和汽车工业的发展，全球汽车保有量也在快速增长，在给人们出行带来便利的同时，也带来了一些负面影响。据世界卫生组织2019 年发布的全球道路安全现状报告显示：交通事故每年夺走超135 万人的生命，这也是5～29 岁人群死亡的主要原因；驾驶员因素导致交通事故的比例明显大于机械故障[1]。因此，汽车行驶的平顺性和安全性成为汽车行业及社会关注的重点。自动驾驶发展已进入L2～L3 阶段，其中先进驾驶辅助系统(advanced driving assistance system，ADAS)[2]主要包括自动紧急制动(autonomous emergency braking,AEB)[3]、自适应巡航控制(adaptive cruise control,ACC)[4]、车道保持辅助(lane keeping assist,LKA)[5]、交通拥堵辅助(traffic jam assist,TJA)[6]等。车辆的横向控制是自动驾驶的核心技术之一，关系到自动驾驶的安全舒适和经济性，作为ADAS的重要分支，车道保持系统通过控制电动助力转向(electronic power steering，EPS)为驾驶员提供转向控制并辅助驾驶员使车辆保持在自身车道内；通过主动的转向方向矫正协助驾驶员，避免无意的方向偏离，同时又不干扰驾驶员的安全驾驶，对车辆横向控制和安全性[7]起到重要作用。

对于车道保持辅助，诸多学者设计了相关策略：朱晨曦等[8]设计了基于自适应模型预测车道保持的四轮转向控制策略，该策略具有良好的横向控制稳定性和车道保持控制精度，但对芯片算力要求高；王家恩[9]通过新车道线检测方案优化预瞄距离，使车辆能稳定跟踪车道；王延宁[10]设计了基于神经网络的自学习功能实时调节PID参数的车道保持辅助系统控制策略，该策略设计简单、响应速度快，但需自学习的过程，且易发生超调现象。线性二次型调节器(linear quadratic regulator,LQR)将侧向速度、横摆角速度、侧向路径偏移和横摆角误差作为状态变量来综合分析控制器的控制效果，能兼顾多个性能指标的同时，易于得到状态线性反馈的最优控制规律，形成控制算法闭环流程[11]，其对车辆芯片算力要求不高、控制精度较高。鉴于此，文中采用LQR设计LKA算法，实现车道保持系统的闭环设计且进行仿真验证，结果表明，该控制策略在较严苛的工况下也能保证最大侧向路径偏移控制在0.28 m以下，最大前轮转角控制在1.5°以下。

1 汽车侧向动力学数学模型

1.1 假设条件

四轮转向(4W S)系统可控制前后轮的转动，为直观简便地分析控制器对前后轮转角的控制，文中在前后轮二自由度模型下建立汽车简化模型，如图1。影响汽车操纵稳定性最主要的因素为车辆质心位置和轮胎侧偏特性，由此提出以下假设：

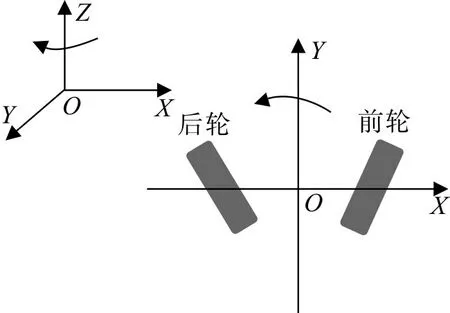
图1 简化的汽车二自由度数学模型Fig.1 A simplified mathematical model of two-degreeof-freedom vehicle

1) 忽略转向系统的影响，以前后轮转角为输入，转角直接输入给转向轮，没有通过方向盘传递给转角；

2) 忽略悬架作用，只做平行于地面的平行运动，沿Z轴位移、绕Y轴俯仰角及绕X轴侧倾角均为零；

3)汽车沿X轴均速运动，即纵向加速度aX=0；

4)同一车轴左右车轮侧偏刚度相同，不计地面切向力、外倾侧向力、回正力矩、垂直载荷变化对轮胎侧偏刚度的影响[12]。

最终，将汽车简化为沿Y轴的侧向运动和沿Z轴的横摆运动，考虑到轮胎特性，将汽车侧向加速度限定在0.4g[13]以下。

1.2 车辆坐标系

车辆坐标系原点与汽车质心重合，车辆的质量分布参数如转动惯量对动坐标系而言为常数[14]。故只需将汽车的绝对加速度、绝对角加速度及外力和外力矩沿车辆坐标系的轴线进行分解，即可列出车辆运动微分方程，图2为汽车侧向动力学受力模型。图中：a，b分别为前后轮距离质心的位置；L为前后轴间轴距；δf，δr分别为前后轮转角；u1，u2分别为前后轮实际前进速度；φ为航向角；∂1，∂2分别为前后轮的侧偏角；FY1，FY2分别为地面对前后轮的侧向反作用力；ωr为绕Z轴的横摆角速度；v为沿Y轴的侧向速度。

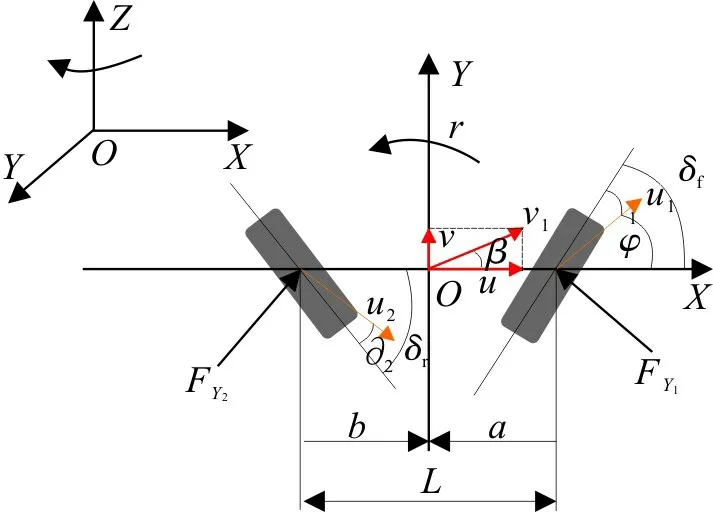
图2 汽车侧向动力学受力模型Fig.2 Lateral dynamic force model of vehicle

1.3 侧向动力学模型

1.3.1 汽车质心绝对加速度分量

汽车动力学分析如图3。图中：OX，OY分别为车辆坐标系的纵横轴；v1为质心速度；u，v分别为车辆沿X，Y轴的运动速度。

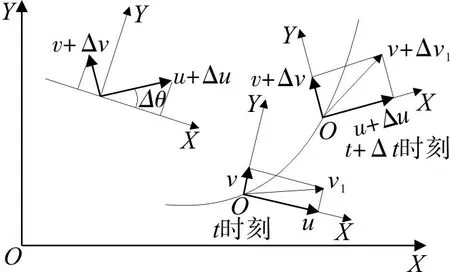
图3 汽车动力学分析Fig.3 Vehicle dynamics analysis

车辆在行进过程中，t到t+ △t时刻沿OX轴速度分量的变化为：

两时刻速度方向的夹角Δθ较小，故cosΔθ可等价为1，sinΔθ等价为Δθ：

由牛顿第一定律可知

最终得到四轮转向的线性二自由度[15]的车辆模型。

2 LQR算法的设计

文中采用LQR 算法实现车道保持系统的闭环设计，设计的汽车控制算法闭环流程如图4。

图4 汽车控制算法闭环流程Fig.4 Lateral dynamic force model of vehicle

在该控制系统中，控制输入为前后轮转角δf和δr，车辆稳定性由侧向速度v和横摆角速度ωr来体现，车道保持的效果由车辆侧向路径偏移y和横摆角误差ψ来反映，车辆的状态会反馈给控制器使误差最小化。车辆当前位置及其方位角与期望路径的关系如图5。

图5 车辆当前位置及其方位角与期望路径的关系Fig.5 Relationship between the vehicle’s current position and its azimuth and the desired path

车辆质心处沿道路法向的速度vn可表示为

3 LKA仿真及结果分析

3.1 Simulink/CarSim联合仿真

利用CarSim 中车辆模型和驾驶员模型及其可与Simulink实时快速地相互调用数据建立汽车联合仿真模型，实现对数据的采集，且将数据图表化[17]。根据前后轮转角的方程式(45)，(46)，在Simulink 与CarSim中搭建联合仿真模型，其中CarSim模块的输出接口变量见表1。

表1 CarSim输出变量Tab.1 CarSim output variable

通过控制器计算将CarSim 的输出变量转化为前后轮转角，同时通过折算齿条位移将前后轮转角转化为方向盘转角信号，且将其作为CarSim 整车模型的输入进行反馈调节[18]，实现Simulink和CarSim的联合仿真，见图6。由图6可知，车道保持辅助系统大致包括3个模块。

图6 Simulink/CarSim联合仿真模型Fig.6 Simulink/CarSim co-simulation model

1)车道偏离检测模块将检测到的汽车和车道中心线之间的偏移量与车道辅助偏移输入进行比较。

2)车道保持控制器模块车道保持控制器根据车辆侧向速度、横摆角速度、侧向路径偏移和横摆角误差计算得到前轮转角，控制车辆保持在车道上行驶。

3)应用辅助模块驾驶员如果打方向灯变道或未打方向灯变道，方向盘则会检测驾驶员输入的力矩，一般力矩大于3 N•m 时由驾驶员接管车辆，利用辅助模块对车道偏离检测模块失效时产生的误矫正对其进行辅助矫正[19-20]。

3.2 仿真设置与结果分析

车速和道路曲率(C)变化会对车道保持的控制效果造成影响，故设置40，80 km/h 车速及0.010，0.005 m-1道路曲率4种仿真工况，如图7。先设置一段直线路段，接着进入不同曲率的蛇形弯道，最后进入平直道路。4种工况下侧偏位移和前轮转角的响应曲线如图8～11。

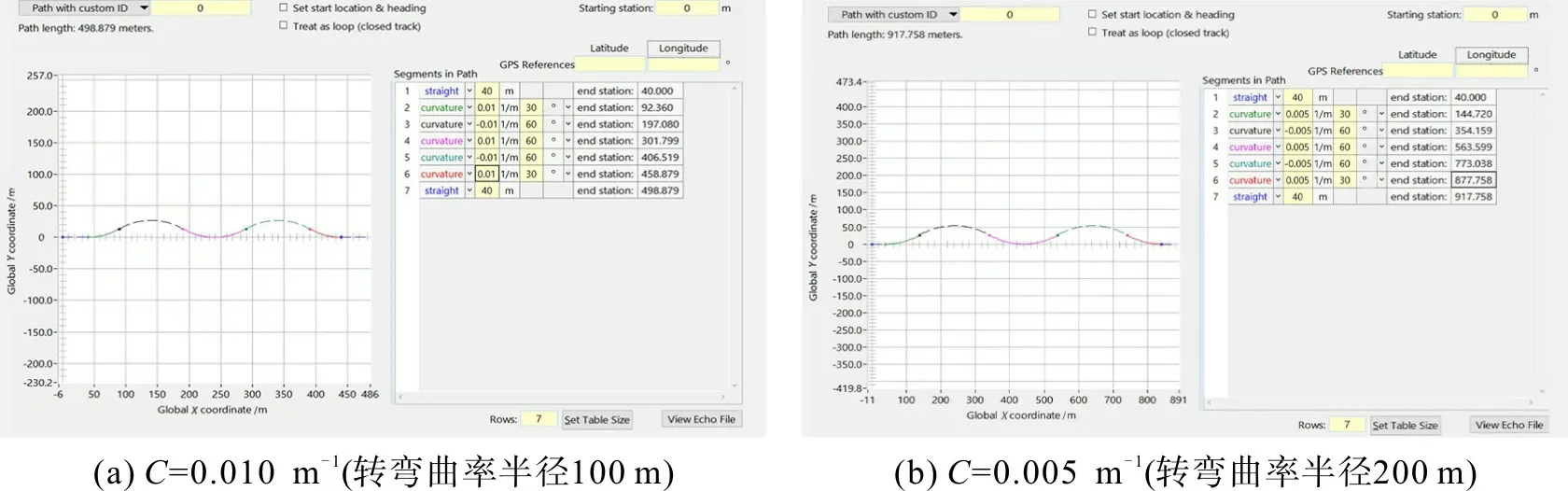
图7 CarSim中不同曲率的蛇形道路设置Fig.7 Serpentine road setup with different curvatures in CarSim

图8 v=40 km/h时不同道路曲率时控制系统的动态响应Fig.8 Dynamic response of the control system under different road curvatures with v=40 km/h

图9 v=80 km/h时不同道路曲率时控制系统的动态响应Fig.9 Dynamic response of the control system under different road curvatures with v=80 km/h

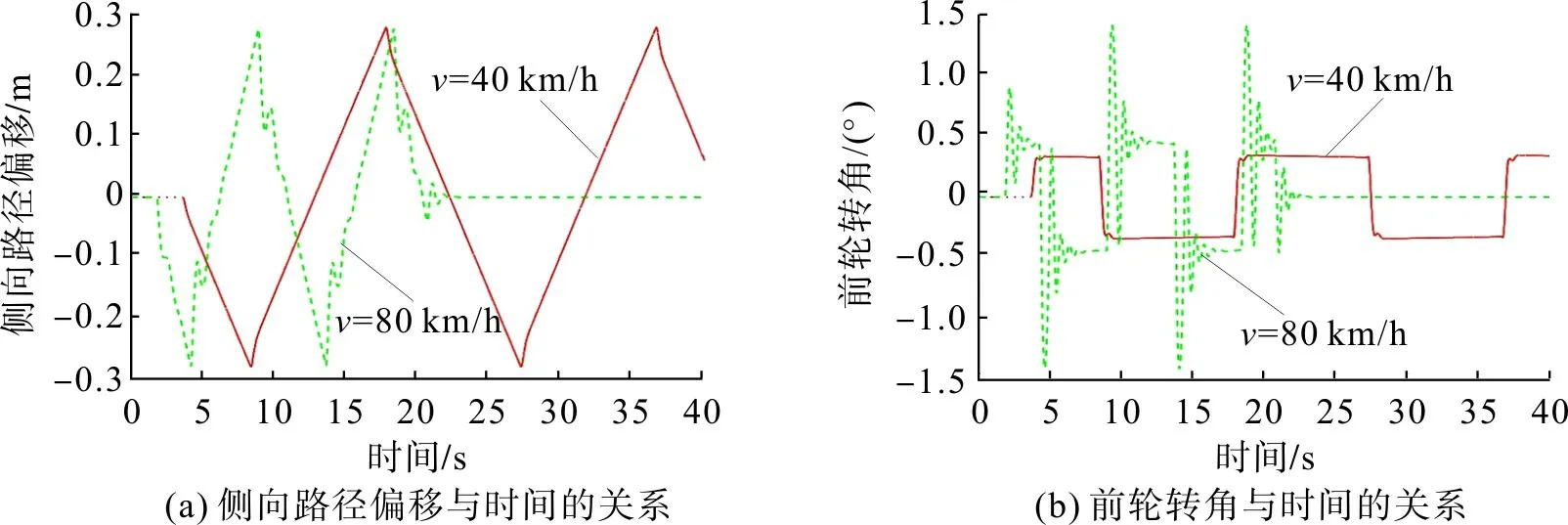
图10 C=0.010 m-1时不同速度时控制系统的动态响应Fig.10 Dynamic response of the control system at different speeds with C=0.010 m-1

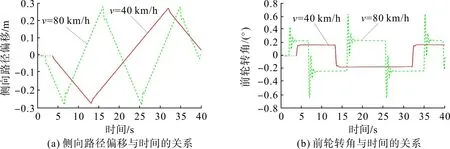
图11 C=0.005 m-1时不同速度时控制系统的动态响应Fig.11 Dynamic response of the control system at different speeds with C=0.005 m-1

对比分析图8～11(b)可知：以图中Y轴零点为车道中心线，当侧向路径偏移和前轮转角为正时，说明车辆靠中心线右侧行驶；当侧向路径偏移和前轮转角为负时，说明车辆靠中心线左侧行驶，直线路段车道保持效果好，侧向偏移和前轮转角均为0；当车辆入弯时，车辆侧向路径偏移和前轮转角开始发生变化。对比图8(a)，9(a)，10(a)，11(a)可知：车辆在高低速和高低曲率下，均能将侧向路径偏移控制在0.28 m以下且持续时间较短，考虑到车道保持功能的开启多为高速情况，为使车辆在高速行驶下不会因车速快速变化而大幅流失车道保持效果，一定程度上牺牲了低速下乘坐的舒适度，但保证了高速情况下车辆的稳定控制及乘坐的安全性。对比图8(b)，9(b)，10(b)，11(b)可知：车辆在高速和高曲率下，前轮转角变化相比低速和低曲率时较大且有轻微抖动，但前轮转角最大也不超过1.5°，乘以车辆转向比(15∶1)换算成方向盘转角约22°。这主要是为使在高速高曲率路况下，快速纠正车辆行进姿态，不断调整前轮转角使侧向路径偏移保持在0.28 m 以下，尽可能地将车辆控制跟随在车道中心线行驶。

CarSim 中显示的期望和实际路径跟踪情况如图12。结合图12 可看出：4 种仿真工况下，车辆均能保持良好的路径跟踪和动态控制；实际路径与期望路径偏差均在可控范围内，体现了控制过程中良好的适应性和鲁棒性。

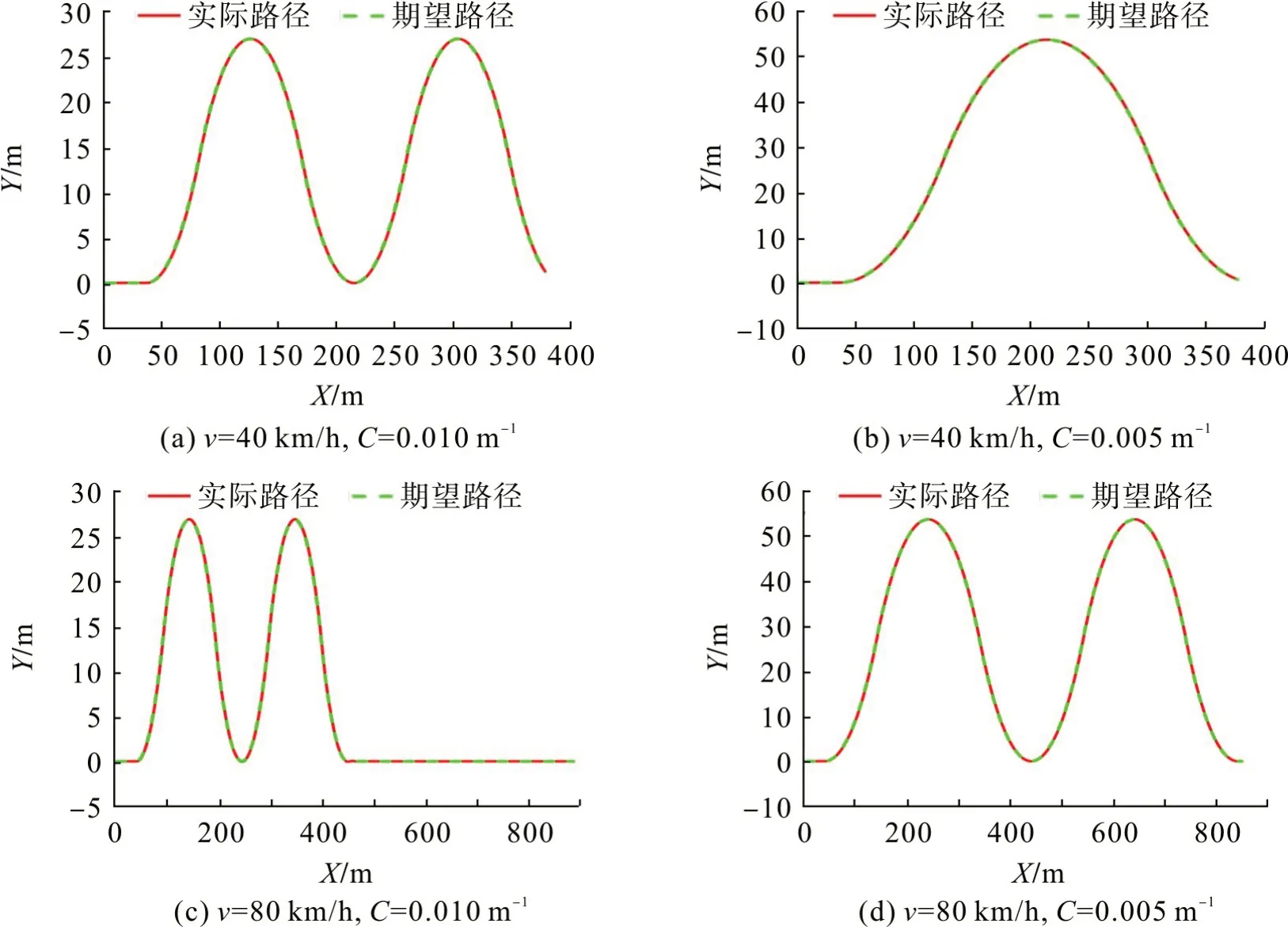
图12 4种工况下的路径跟踪效果Fig.12 Path tracking effect under four working conditions

4 结论

建立二自由度四轮转向车辆模型，分析车辆在行驶过程中的侧向动力学，设计基于线性二次型调节器(LQR)的控制策略；经过Simulink/CarSim 联合仿真，得到高低曲率、高低速度下侧向路径偏移和前轮转角的动态响应。仿真结果表明：该控制策略在上述4种路况下可将侧向路径偏移控制在0.28 m 以下，最大前轮转角控制在1.5°以下；偏差出现时间较短，即该控制策略可快速消除控制误差，保证车辆跟随车道中心线稳定行驶，有效实现了车辆的动态响应，本控制策略具有良好的鲁棒性和适应性。