基于SEM的曲线段钢轨伤损影响因素量化研究

王 宁，杨康华，何 庆，高天赐，王启航，王 平，刘 勇

(1.中国铁路西安局集团有限公司，西安 710054；2.西南交通大学 a.高速铁路线路工程教育部重点实验室，b.土木工程学院，成都 610031；3.中国铁路成都局集团有限公司，成都 610082)

随着铁路运输朝着重载和高速方向发展，钢轨伤损发展速度明显增加.特别是在小半径曲线段，由于钢轨的导向作用，轮对和钢轨之间存在挤压、黏着、滑动，尤其是小曲线半径段外侧的钢轨，钢轨伤损更为严重，不仅增加线路的养护维修成本，降低行车质量，还会大幅缩短钢轨的使用寿命.分析量化钢轨伤损影响因素，用于指导日常钢轨养护维护已成为亟需研究的课题.

前期的研究工作中，学者已经对钢轨伤损的影响因素进行了探究.文献[1]通过分析研究出现剥离掉块、水平裂纹病害的钢轨，利用SIMPACK建立车辆-轨道模型，模拟分析了运行速度、曲线半径、轨底坡、曲线超高等参数对曲线段钢轨受力与稳定性的影响，提出防治曲线钢轨病害的最有效途径是设置较大的曲线半径.文献[2]通过建立列车-轨道模型,分析了列车在不同曲线半径、外轨超高、轨底坡、轨距、轴重等参数条件下通过曲线地段对钢轨磨耗产生的影响，分析表明在小半径曲线、短缓和曲线下，轮轨间作用越剧烈，钢轨越容易产生磨耗问题.文献[3]通过轮轨实验表明，钢轨的磨耗对滚动疲劳裂纹(Rolling Contact Fatigue，RCF)的发展有重要的影响，磨耗对钢轨表面细微裂纹有打磨作用，在钢轨磨耗量大的情况下，疲劳裂纹深度较浅，甚至疲劳裂纹会因钢轨磨耗的作用消失.文献[4]建立了一个包含运营条件的机车车辆-线路的动力学分析模型，分析了曲线段侧面磨耗的形成机理和影响因素，指出严重的钢轨侧面磨耗会减少钢轨的强度，加剧钢轨的伤损.文献[5]通过对大秦线的钢轨伤损规律的分析，得出侧面磨耗是影响小半径曲线上股钢轨使用寿命的关键因素.文献[6]利用贝叶斯生存分析方法，分析了轨道几何缺陷、列车通过总重、区段道岔数量等风险因素对钢轨伤损出现概率的影响，并绘制了钢轨的生存函数曲线.文献[7]通过对1990年至2014年的铁路设备事故数据集进行分析，结果表明，铁路设备事故数量的变化趋势与铁路服务里程的变化趋势一致.文献[8]通过研究磨耗和疲劳伤损的竞争关系，提出通过改善磨耗，优化钢轨廓形的方式来减少钢轨伤损，增加钢轨的疲劳寿命.

虽然目前关于钢轨伤损原因的文献较多，但存在一些不足：①现阶段对钢轨伤损原因的分析研究还仅停留在实验分析和数值仿真分析阶段，缺乏对大量实际数据的分析挖掘；②在研究各因素影响程度时，通常都会假定其他因素不变，但实际情况下各影响因素是共同作用于钢轨；③大多数研究仅分析了钢轨伤损影响因素，并未将各因素对钢轨伤损的影响程度进行研究，未能抓住影响钢轨伤损最重要的因素.因此,本文作者根据西南某局实际伤损数据，系统分析钢轨相关数据之间的影响路径和影响程度，对日常养护维修、合理分配维护资源、提高钢轨探伤效率有一定的参考价值.

1 钢轨伤损与磨耗关系分析模型

1.1 结构方程模型

不同服役环境下的钢轨伤损和磨耗量都存在很大差异，它们之间的关系是错综复杂的，伤损的影响因素之间存在多维度、共同的作用.传统的多元线性回归模型只能分析单一自变量对因变量的影响，隐含其他变量不变的假定，无法满足钢轨伤损复杂影响关系研究中多个复杂变量同时作用的分析要求.并且传统分析方法仅能分析出单变量间的影响方向和影响程度，不能展示变量间的影响路径和因果关系，无法直观地展现各变量之间的关系.

面对此情况，结构方程模型(Structural Equation Model，SEM)是一种有效的分析手段，因为结构方程模型不是纯粹的数理方法，它融合了传统多变量统计分析中“因素分析”和“线形回归分析”的统计技术[9]，并且可以将钢轨伤损和磨耗的实际分析经验加入到分析中，这样能够避免很多无效的分析过程，同时能对数据中蕴含的信息进行更为深入的挖掘，并对多变量之间的交互关系进行定量分析.结构方程模型的方程表达式为

η=Bη+Γξ+ζ

(1)

Y=Λyη+ε

(2)

X=Λxξ+δ

(3)

模型要求观察变量服从多元正态分布，基本方程中变量矩阵的定义见表1.

表1 基本方程中变量的定义

由于变量间的关系错综复杂，有单向影响关系，也有互相影响关系，可以采用结构方程模型对多元变量进行逐步解析.结构方程模型的路径图可以更加清晰地表示复杂的关系，如图1所示.

图1 结构方程模型路径图

图中方形变量代表可测量的“显变量”，圆形变量表示不可直接测得的“潜变量”，通过显变量表示潜变量的部分称为潜变量测量模型.其中包含潜变量测量模型的称为潜变量模型，不包含潜变量测量模型，均为显变量的模型称为路径模型；变量之间的关系通过连线表示，单箭头表示一个变量对另一个变量的影响，二者之间存在因果关系；双向箭头表示两个变量的关联，但不表示变量之间的效应.模型的输出值是影响路径的因子荷载，即表示自变量对因变量的影响程度.

1.2 模型参数估计

结构方程模型的估计是极小化样本协方差与模型估计协方差之间的关系.由于本文中钢轨伤损程度数据中存在序列变量的情况，所以采用具有均值和方差的加权最小二乘法(Weight Least Square With Mean And Variance，WLSMV)[10].加权最小二乘法的适配函数为

FWLS=[s-σ(θ)]TW-1[s-σ(θ)]

(4)

式中：s为由样本协方差矩阵的非重叠部分组成的向量，元素个数为1/2(p+q)(p+q+1)；σ(θ)是估计值θ所求得的协方差矩阵中非重叠部分所组成的向量；W-1为正定加权矩阵.通过计算适配函数FWLS的最小值，从而求得θ的估计值.WLSMV是在加权最小二次法(Weight Least Square，WLS)的基础上发展出来的估算法，该方法考虑了数据的均值和方差，更能符合估算过程的正确性.

2 构建伤损结构方程模型

2.1 数据来源及预处理

2.1.1 钢轨伤损数据

本文选取的伤损数据来自西南某局下辖的三条I级铁路，运营速度为80～120 km/h，伤损时间为2011年-2019年.在钢轨伤损记录中基于铁路工务部门根据钢轨各类病害严重程度，定义了钢轨的伤损程度，共有4个等级：轻伤、轻伤有发展、重伤、折断，其中重伤和折断的钢轨需要立即进行换轨处理.在钢轨伤损数据中，曲线段外轨钢轨重伤数量的占比达到82.2%，所以本文选择小曲线半径下的外侧钢轨作为研究对象，选取半径小于1 200 m的小曲线半径外轨数据共4 447条，其中无伤1 894条、轻伤1 878条、轻伤有发展趋势96条、重伤572条、折断7条，伤损均为钢轨轨头伤损(无磨耗超限伤损).并将伤损数据与线形数据、运量数据在里程上实现融合.

2.1.2 钢轨磨耗数据

本文的磨耗数据为2017年10月至2018年2月测得的三线的磨耗记录，包含测点里程、侧磨、垂磨、曲线半径、钢轨年份等数据.磨耗采集使用的是MiniProf廓形仪，测量精度为0.01 mm.对于曲线段的磨耗测量，设置的测量点不少于5个，即直缓(ZH)、缓圆(HY)、曲中(QZ)、圆缓(YH)和缓直(HZ).当圆曲线长度L为500 m(不含)至1 000 m时，曲线段采集2个测点，以此类推，圆曲线长度L每增加500 m增加一个测点，且圆曲线区段各测点均匀布置，如图2所示.

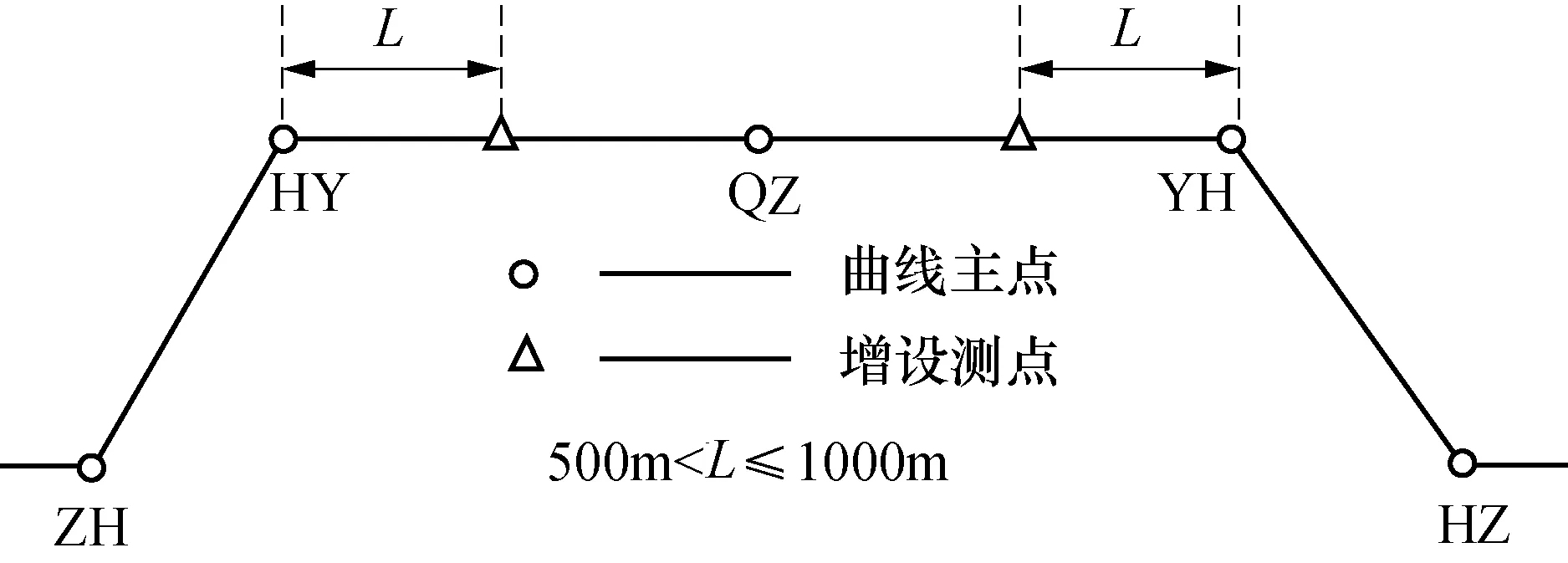
图2 磨耗数据测点分布情况

2.1.3 基于多体动力学软件的钢轨磨耗数据修正

钢轨伤损数据和磨耗数据是相互独立的，它们不是同一时间测得，如钢轨伤损的记录时间是t1，磨耗测量时间是t2，对应测量磨耗量为w，两种数据之间存在时间差及运量差.为了挖掘钢轨伤损和磨耗之间的关系，需要对钢轨磨耗进行修正，利用时间差对应的运量，将磨耗换算回刚好出现伤损时的磨耗量.采用动力学仿真软件Universal Mechanism(UM)来对磨耗数据进行调整，在UM软件的磨耗计算模块中选用Archard模型进行磨耗计算[11]，通过计算绘制得到通过总重与钢轨磨耗关系曲线，如图3所示.

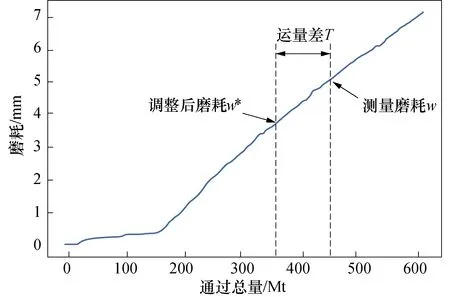
图3 曲线半径R=750 m曲线外轨通过总重与钢轨磨耗关系曲线

将钢轨伤损和磨耗测量的时间差换算成运量差，再根据运量差换算得到调整后的磨耗，换算公式为

w*=w+Ta

(5)

式中：w*为调整后的钢轨磨耗，mm；w为记录时的钢轨磨耗，mm；T为钢轨伤损记录时刻t1和磨耗测量时刻t2之间的运量差，Mt；a为每百万吨运量所对应的磨耗量，分段进行计算.通过对模型参数的调整，可以获得不同工况下的通过总重和钢轨磨耗关系曲线.

2.1.4 有序变量处理

由于钢轨伤损程度数据为有序分类数据(0-无伤、1-轻伤、2-轻伤有发展、3-重伤、4-折断)，需要对各程度间的阈值τ进行估计.可以用基本连续变量近似估计该有序类别变量，由于这个连续变量不能直接观察到，所以称它为潜在变量响应变量，即y*.有序变量的潜在响应变量回归模型为

y*=β1x1+β2x2+…+βpxp+o=Xβ+o

(6)

当y=k时，y*介于τk-1和τk之间，那么概率为

P(y=k|X)=P(τk-1

P(τk-1

P(τk-1-Xβ

(7)

随机变量ε在两个值之间的概率可以转换为这些值处累积分布函数(Cumulative Distribution Function，CDF)值的差值，因此有：

P(y=k)=P(o<τk-Xβ|X)-

P(o<τk-1-Xβ|X)=

Φ(τk-Xβ)-Φ(τk-1-Xβ)

(8)

其中，Φ(τ0-Xβ)=0，Φ(τk-Xβ)=1.累计概率为

P(y≤k|X)=Φ(τk-Xβ|X)

(9)

2.2 数据正态性分析

一般而言，为了保障模型的稳定性，结构方程模型的数据量不得偏低.本文中选取的样本个数为4 447，能达到模型的数据量要求.作为模型的输入，理论上样本数据需要呈正态分布，但实际很难获得完全多元正态分布的钢轨数据.所以，在实际分析中很多学者认为只要样本数据不存在很严重的非正态性，即可采用结构方程模型进行分析[12].因此，本文通过考察变量的偏度(skewness)和峰度(kurtosis)，采用较为客观的统计判定法来分析数据的正态性.计算结果如表2所示.

表2 样本统计描述

单变量的正态分布检验可以通过偏度和峰度的绝对值来判断[13].由表2可知，在偏度方面，所有变量偏度的绝对值都小于3；在峰度方面，所有变量峰度的绝对值都远小于20.计算结果表明样本数据不存在严重的非正态性，可作为结构方程模型的输入变量.处理后的数据集如表3所示.

表3 处理后数据集(部分)

2.3 结构方程模型构建

2.3.1 模型边界

样本数据包括线形数据(外轨超高、曲线半径、缓和曲线长度)，磨耗数据(侧面磨耗、垂直磨耗)，还包括运量数据和钢轨伤损数据，不包含无法直接测量的潜变量.由于本文所使用的数据均来自实际养护维修中的真实数据，因此不再进行信度和效度检验[9].

2.3.2 模型的结构关系构建

线形数据、总运量对钢轨的磨耗和伤损均有直接影响[1-5]，因此在模型中构建了线形数据和运量对磨耗和伤损的单向箭头；除此之外，线路的曲线半径、超高、缓和曲线长度等数据在线路设计时是综合考虑的，故它们之间存在相互影响的关系，因此构建了线形数据之间相互影响的双向箭头，如图4所示.

图4 钢轨伤损与磨耗关系的结构关系图

3 实证分析结果

3.1 模型的拟合优度

用Mplus软件对图4构建的模型进行拟合，经过反复修正后，得到拟合结果.目前常见的拟合度评价指标有χ2/df、CFI和RMSEA等，模型拟合结果如表4所示.由表4可知，模型拟合指标均符合检验标准.χ2/df、RESEA、TLI、CFI值分别为11.563、0.049、0.966、0.992，均在可接受范围内，且效果较好.可以判断该结构方程模型总体上效果较好.

表4 模型拟合结果与指标参考标准

3.2 模型输出结果

各变量之间的具体影响关系及影响系数见表5.

表5 路径系数估计值

表中标准化估计值的绝对值表示两个变量之间关系的影响程度，其中正数表示影响为正相关，负数表示影响为负相关；非标准化估计值表示自变量单位变化对因变量的影响；P值表示影响是否显著，当P值小于0.05时,表示在统计学上显著.

对钢轨伤损程度的有序分类变量进行处理，获得相应的潜在响应变量y*,见图5，其中τ1、τ2、τ3、τ4分别表示无伤和轻伤、轻松和轻伤有发展、轻伤有发展和重伤、重伤和折断状态之间的阈值.

图5 钢轨伤损程度潜在响应变量y*

钢轨伤损与磨耗关系的路径模型的标准化系数如图6所示.

自变量对因变量的影响可分为直接因果效应和间接因果效应[14]，其中直接因果效应是自变量直接作用于因变量上，如曲线半径--->伤损；间接因果效应是自变量通过作用于其他变量间接作用于因变量，如曲线半径--->侧磨--->伤损.通过对图6(a)标准化系数的数据整理，获得各项因素对钢轨伤损影响的总效应，如表6所示.

表6 各项因素对钢轨伤损影响强度表

通过分析各因素对钢轨伤损影响的路径和强度，得到曲线半径、超高、缓长、侧磨、垂磨和总运量对伤损的影响分别为-0.287、-0.135、-0.014、0.466、-0.290和0.477.即曲线半径、超高、缓长、侧磨、垂磨和总运量等数据的标准差每增加1，相应的钢轨伤损将增加-0.287、-0.135、-0.014、0.466、-0.290和0.477.其中正值表示伤损程度随着标准差的增加而增加，反之则减少.

由图6(b)可知，在曲线半径R<1 200 m的情况下，总运量每增加10 Mt，侧面磨耗和垂直磨耗分别增加0.044 mm和0.007 mm，钢轨伤损程度潜在响应变量y*增加0.012；侧面磨耗、垂直磨耗每增加1 mm，钢轨伤损程度潜在响应变量y*分别增加0.278和减少0.153；在相同通过总重情况下，曲线半径每增加100 m，侧面磨耗和垂直磨耗分别减少0.24 mm和0.102 mm，y*减少0.089；超高每增加1 mm，侧面磨耗和垂直磨耗分别减少0.014 4 mm和0.013 9 mm，y*减少0.004 7；缓和曲线每增加100 m，侧面磨耗和垂直磨耗分别减少0.57 mm和0.73 mm.

图6 钢轨伤损影响因素结果输出图

4 结论

1)各因素对钢轨伤损程度的影响强度排名为：总运量、侧磨、垂磨、曲线半径、超高、缓和曲线长度.

2)侧面磨耗对钢轨伤损程度影响较大，侧面磨耗的增加会减少轮轨接触面积，并且会降低钢轨的强度，从而加剧钢轨的伤损.

3)垂直磨耗对钢轨伤损情况也有较大影响，钢轨垂直磨耗的增加对深度较浅的疲劳裂纹存在打磨作用，可以避免细微裂纹发展为伤损，从而减少疲劳伤损的发生，二者呈明显的竞争关系.

4)在相同曲线情况下，总运量每增加10 Mt，侧面磨耗和垂直磨耗分别增加0.044 mm和0.007 mm；在相同通过总重情况下，曲线半径每增加100 m，侧面磨耗和垂直磨耗分别减少0.24 mm和0.102 mm；超高每增加10 mm，侧面磨耗和垂直磨耗分别减少0.144 mm和0.139 mm；缓和曲线每增加100 m，侧面磨耗和垂直磨耗分别减少0.57 mm和0.73 mm.

5)在曲线半径较小且侧面磨耗较大的地段，应增加探伤频次；在曲线半径较大且侧面磨耗较小的地段，可根据实际情况适当延长探伤间隔.