赛事公交车辆路径优化研究——以2022年北京冬奥为例

官云林，王 云，闫学东，郭浩楠

(北京交通大学 a.交通运输学院, b.综合交通运输大数据应用技术交通运输应用技术交通运输行业重点实验室，北京 100044)

国际重大赛事活动会吸引百万级游客和全球媒体的关注[1].在2012年伦敦奥运会期间，有1 000万观赛人群现场观看了由29个比赛场馆举行的各类赛事项目，日高峰观众人数超过80万[2].海量的国内外观赛人群在短短几周的赛事活动期间内聚集在举办城市中，随之激增的观赛出行需求加大了常规交通系统的服务压力，导致出现道路交通安全隐患、出行服务水平低、赛事观众出行效率低等问题[3-5].

国内外的许多学者从调整赛事举办城市的全域综合交通系统规划、限制日常交通出行、加强交通基础设施建设等方面展开研究.Currie等[6]总结了2012伦敦奥运期间通过大规模的交通需求管理调整居民的日常交通出行方式，提出城市交通规划管理策略以适应赛事人群激增的出行需求.面对观赛出行的压力，Kassens-Noor[7]分析2024年波士顿奥运会交通规划方案发现其计划增加了决策成本，同时大量交通发展空间被压缩.除了减少日常出行需求外，许多城市还将大型活动视为交通发展的巨大机遇.通过建设铁路、高速公路、地铁线路等增加交通资源以服务新增观赛出行需求[8-9].北京市在筹备2008年奥运会期间，投资了超过200亿美元用于交通相关项目，地铁网络从3线扩展到7线系统，其中包括机场专用铁路[10].然而调整城市总体交通规划对当地居民的日常出行影响巨大，增加交通基础设施建设的时间和经济成本也极其高昂，同时上述方法难以适应场馆之间观赛人群灵活的出行需求，提出补充场馆间交通方式是十分有必要的.

考虑到2022年北京冬季奥运会是世界首次开展的多赛区多场馆奥运会，会在北京城区、延庆、张家口赛区之间及内部的场馆间新增大量出行需求.本文作者提出以观赛人群出行需求为导向的赛事公交服务来缓解常规交通系统压力，并保证场馆间交通出行效率和服务质量.基于车辆路径问题(Vehicle Routing Problem，VRP)[11-13]，着重考虑时间窗、载量约束，以运营车辆使用、开行成本最小为目标构建优化模型，并通过两种有效不等式和基于最优时差插入法的遗传算法实现不同规模算例的求解.

1 赛事公交车辆路径优化模型

基于带时间窗和载量约束的车辆路径问题(Vehicle Routing Problem with Pickup and Delivery and Time Window, VRPPDTW)构建赛事公交车辆路径优化模型，具体问题假设条件如下：

1)每个出行需求接送客节点、乘客数量和时间窗信息已知.两场赛事间出行乘客时间窗相同，且所包含的乘客数量小于赛事公交载客能力.

2)任意出行需求均需在时间窗内有且仅被服务一次，且同一出行需求由一辆赛事公交完成接送服务.

3)任意出行需求的接送客最大时间间隔均大于或等于赛事公交在对应接送节点间开行时间.

4)车库仅有一个且位置固定不变，所有赛事公交从车库出发，最后返回车库.

5)赛事公交车辆同质，在时间窗约束和载量约束条件下可进行混合搭载.

设P={1,2，…,n}为接客点集合，D={n+1,n+2，…,2n}为送客点集合，接送客节点并非物理意义上的接送客站点，而是构成出行需求的接送客节点，同时有A=P∪D.每个出行需求采用(i,n+i)表示，均由一个或多个时间窗相同、接送节点相同的观赛人群在场馆间的出行构成.设K为赛事公交车辆集合.设0-1决策变量xi,j,k判断赛事公交k是否经过有向弧(i,j)，Ti,k和Li,k分别表示赛事公交k到达节点i的时间和服务后的载量状态.构建赛事公交车辆路径优化模型为

(1)

(2)

(3)

(4)

∀j∈A,∀k∈K

(5)

∀i∈P,∀k∈K

(6)

ai≤Ti,k≤bi∀i∈A,∀k∈K

(7)

Ti,k+Si+ti,j,k≤Tj,k+M(1-xi,j,k)

∀i∈A,∀j∈A,∀k∈K

(8)

Ti,k+Si+ti,n+i,k≤Tn+i,k

(9)

Li,k+lj,k≤Lj,k+M(1-xi,j,k)

∀i∈A,∀j∈P,∀k∈K

(10)

Li,k-lj,k≤Lj,k+M(1-xi,j,k)

∀i∈A,∀j∈D,∀k∈K

(11)

li,k≤Li,k≤Ck∀i∈P,∀k∈K

(12)

0 ≤Li,k≤Ck-li,ki∈D,∀k∈K

(13)

Lo,k=0 ∀k∈K

(14)

xi,j,kbinary ∀k∈K,(i,j)∈A

(15)

2 求解算法

考虑到车辆路径优化属于典型的NP-hard问题，计算求解难度较高，首先利用数学规划优化器Gurobi实现对模型的基本精确计算，得到最优解.然后引入有效不等式方法在基本精确计算的基础上进一步提高计算效率，实现模型求解.最后将上述两种求解算法与禁忌搜索算法和基于最优时差插入法的遗传算法进行对比，判断不同求解策略在计算效率和求解精度上的优化幅度，进而分析基于最优时差插入法的遗传算法求解的准确性和高效性.

2.1 有效不等式方法

基于子路径消除约束和2-path不等式[14]提出与赛事公交接送客服务特征相适应的有效不等式.令集合S表示接乘集合中的任意子集S⊆P，|S|为集合S内元素个数.k(S)为在车辆载客容量约束条件下，可满足集合S内乘客接乘服务的最小用车数.

(16)

(17)

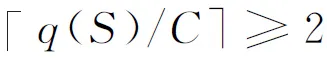
2.2 禁忌搜索算法

利用一种带阈值的禁忌算法对赛事公交车辆路径优化模型进行求解.禁忌算法是目前应用于车辆路径问题最为广泛的启发式算法，其核心是以禁忌列表的形式保存计算遍历过的部分求解信息，进而减少邻域算子搜索过程中陷入循环的情况.

2.2.1 邻域结构

以两条路径间点的插入作为邻域操作策略.随机选择两条路径r1，r2，分别随机任取[0,2]个出行需求，在时间窗及载量约束等条件下将出行需求对应的接送客节点随机插入对方路径中，尝试n次若插入方案均无法满足约束则重新选择两条路径重复邻域操作.同时，因两条路径上的出行需求是在区间[0,2]中随机选择，故本节中点的插入实际上包含了出行需求的转移和互换两种操作.

2.2.2 禁忌和特赦规则

为增加搜索多样性并防止求解循环，引入禁忌列表来储存禁忌对象，用于记录最近接受的移动.定义禁忌周期为Tabu_len，在本文中设定禁忌周期固定不变.同时，考虑到苛刻的禁忌原则使得一些较优解被放弃不利于算法的搜索，设定移动后得到的解优于禁忌列表中对应解时则特赦允许禁忌的移动.

2.2.3 阈值更新规则

最初设置阈值t为0来保障求解质量.当且仅当计算陷入局部最优时，调整阈值t为[0,Tmax]间的随机数以提高求解多样性，其中Tmax为程序阈值的最大值.若得到的解更新了最优可行解，则将阈值t重置为0以增加搜索深度.

2.2.4 搜索策略

通过first_accept搜索策略实现在增加求解多样性的同时降低搜索时间的目标.当邻域算子变换后的解不在禁忌列表中或者满足特赦规则，且解的目标函数值变化小于阈值t时，替换当前最优可行解.

2.3 遗传算法

遗传算法是一种不依赖于梯度，具有随机与高度并行特征的自适应全局域优化概率搜索算法.在遗传算法求解过程中考虑了基于插入前检测的最优时差插入法和随机匹配交叉方法以提高算法求解效率.

2.3.1 插入算子

基于最优时差插入法[15]构建插入算子.如图1所示，插入算子核心在于计算新节点插入位置后面节点实际到达服务时间，并判断是否仍在相应的时间窗范围内.以可行路径Rk(0,i,j,…,i+1,…,j+1,0)为例，具体公式为

图1 基于插入前检测的最优时差插入过程示意图

wj=max{0,aj-(Ti,k+si+ti,j,k)}

∀(i,j)∈Rk,∀k∈K

(18)

∀(i,j)∈Rk,∀k∈K

(19)

(20)

∀(i,j)∈Rk,∀k∈K

(21)

(22)

(23)

∀(i,j)∈Rk,∀l∈Sk∀k∈K

(24)

2.3.2 交叉算子

考虑到染色体片段交叉后仍需满足先接后送原则，同时要符合载量约束和时间窗约束，因此交叉算子以路径作为染色体片段交换的最小单位.采用随机不等交叉算子增加算法搜索步长，如图2所示，在[0,1]范围内随机生成两位小数，若小于交叉概率Pc(Pc≥0)则触发交叉算子计算，从两个父代染色体中分别随机任取一至两条路径完成交换.删除重复需求节点并根据插入算子补全染色体缺失需求点.若现有路径均插入不可行，则在染色体末尾生成一条新路径插入该出行需求.

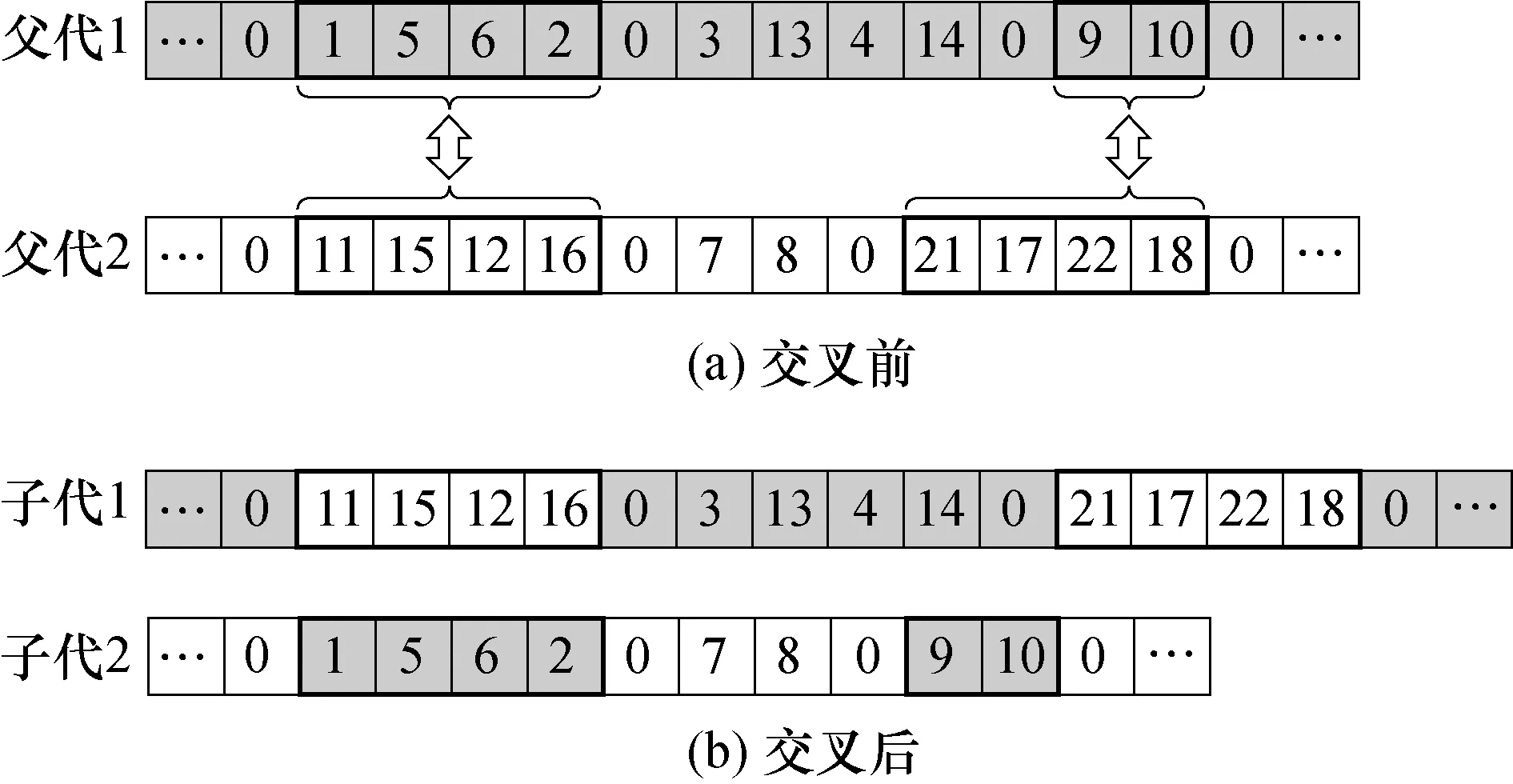
图2 染色体随机交叉示意图

2.3.3 突变算子

突变算子以出行需求作为突变的最小单位，仍需确保每个出行需求先接后送的原则，同时满足载量约束和时间窗约束.图3中，设突变概率Pm在[0,1]范围内随机生成两位小数，若小于突变概率则从父代染色体中随机选取一个路径中的出行需求并将其从该位置删除，在染色体中搜索最优插入位置，根据插入算子确定最终方案.若现有路径插入不可行，则在染色体末尾再生成一条新路径并插入该出行需求.

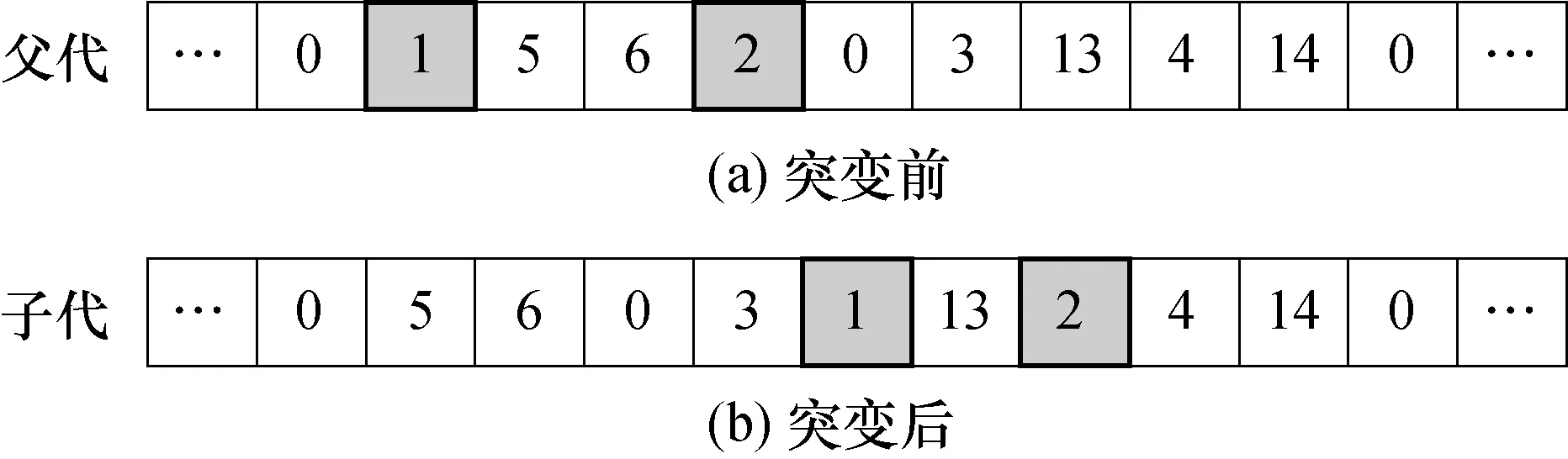
图3 染色体变异过程示意图

突变后形成新的子代染色体种群池，计算每个染色体目标函数值，进行适应度映射后得到染色体适应度，适应度函数为目标函数的倒数.种群池中染色体两两一组选择适应度高的染色体遗传至下一代，进行种群规模次选择形成新的父代染色体种群池重复交叉、突变算子直至满足迭代次数条件.

3 案例分析

以2022年北京冬季奥运会为例进行分析.作为世界首次开展的多赛区冬奥会，2022年北京冬季奥运会包括北京城区、延庆、张家口赛区，共涵盖12个比赛场馆，见图4.为优先对使用车队规模进行优化，可采用设置高于车辆行驶费用数量级的车辆固定使用费用[16]，考虑到北京冬奥赛区间及内部道路网络上车辆实际行驶费用范围，设车辆固定使用费用为1 000元，车辆行驶费用单位为1元/min，同时根据实际赛事活动安排组织足够的赛事公交车队开展服务，车载容量为40人，在接、送客站点停泊时间为5 min.

图4 2022年北京冬季奥运会赛事场馆分布图

设置2022年2月8日内的13个观赛出行需求，数据格式如表1所示，其中各出行需求乘客数之和为184人.利用现有商业化数学规划优化器Gurobi实现对算例的基本精确求解，并与本文有效不等式、禁忌搜索算法和遗传算法计算结果进行比较分析.如表2所示，利用有效不等式能够合理缩小最优解搜索范围，计算效率提升57.3%，并能在可接受计算时间内得到精确结果.而禁忌搜索算法在n=400、Tabu_len=20、Tmax=100，迭代次数为2 000次时，可在34.9 s计算后得到优化目标值误差在8%的可行解，求解精度较高.而采用基于最优时差插入法的遗传算法，设置500种群规模、交叉因子为0.8、突变因子为0.15，共迭代2 000次，能够进一步提高99.4%的计算效率且得到理想的优化结果.分析遗传算法计算结果的产生原因为，模型优先最小化车辆使用成本，优化车辆开行成本的搜索空间受到最小车队规模限制，因此在小规模算例中更易得到理想优化结果，计算表明禁忌搜索算法、遗传算法均具备在有限计算能力和时间条件下完成更大规模计算任务的能力，且后者计算精度更高.

表1 观赛人群出行需求数据格式表

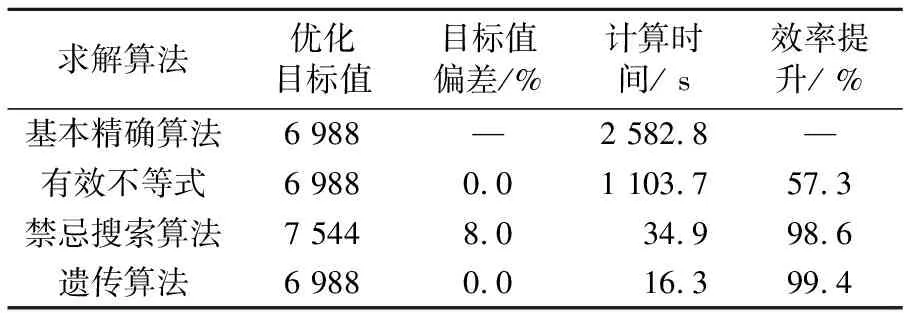
表2 有效不等式和遗传算法计算结果分析

设置2022年2月16日比赛日内的122个出行需求，总乘客数量为1 809人.该算例规模条件下已无法通过有效不等式方法在有限计算条件下获得优化结果.故采用禁忌搜索算法和遗传算法实现优化计算，其中禁忌搜索算法在n=400、Tabu_len=40、Tmax=1 000，迭代次数为200 000次时，可在2 648秒计算后得到目标值为81 353的可行解.同时利用基于最优时差插入法的遗传算法，根据不同种群条件下的交叉、突变概率参数组合可以得到优化目标函数值及相应方案计算时间见表3.由表3可知，在相同种群规模条件下，交叉、突变概率变化对计算的影响主要表现在求解效率上：随着交叉突变概率的提高，触发交叉、突变算子运算的情况更加频繁，从而导致计算时间不断增长.

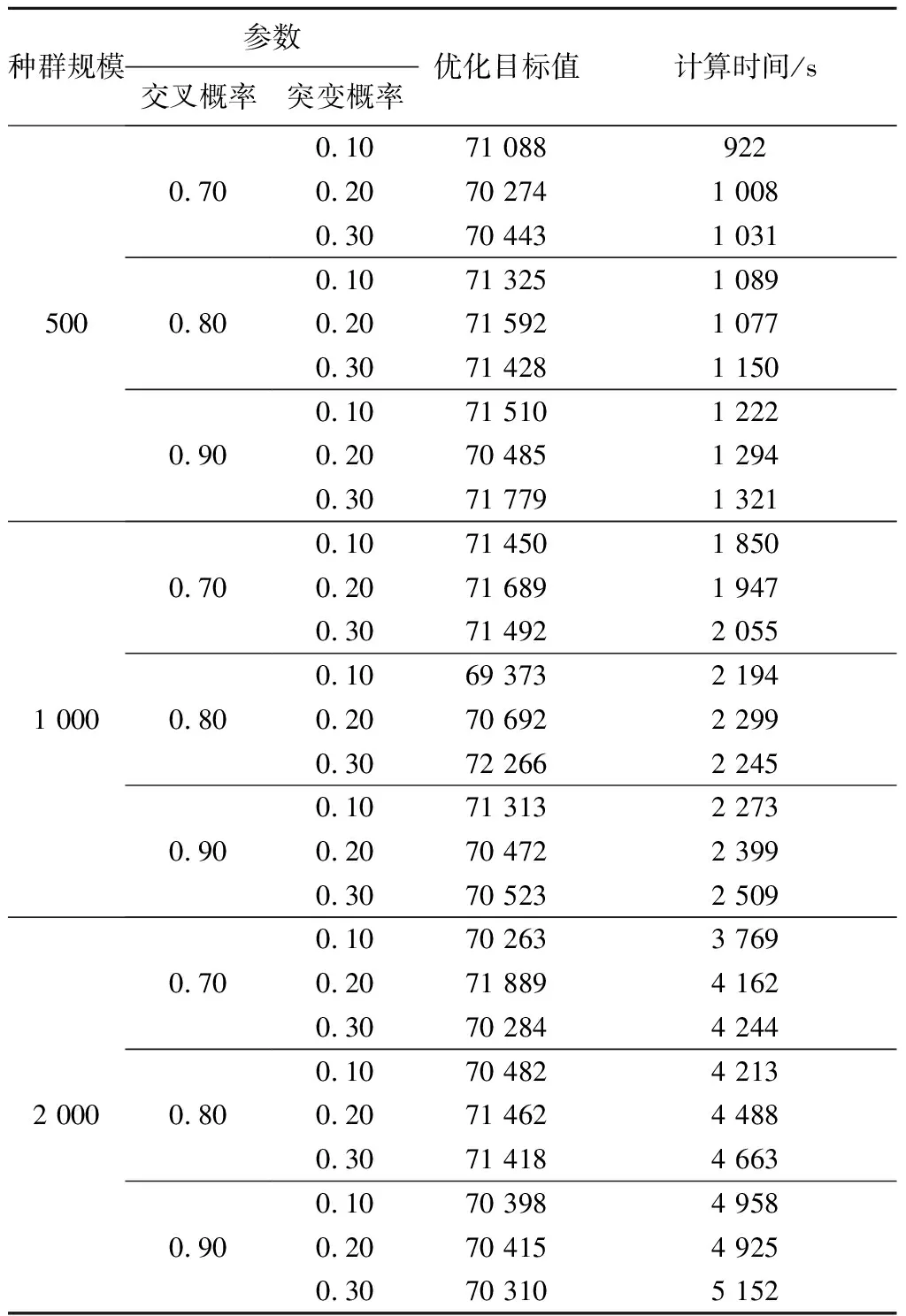
表3 不同交叉、突变参数及种群数量组合计算结果对比

由表3可知，种群规模较小时，计算时间相对较短但求解质量普遍不高，在500种群规模下交叉因子设置为0.7，突变因子为0.1时，求解时间最短，共用时922 s.在2 000种群规模下，设置交叉概率为0.9，突变概率为0.3时，求解时间最长，共用时5 152 s，求解时间相差近5.59倍.与禁忌搜索算法相比，基于最优时差插入法的遗传算法在1 000种群规模下，交叉因子为0.8，突变因子为0.1时，能够在更少的计算时间内求解得到目标值为69 373的较优解.

4 结论

1)面向观赛人群提供需求响应式移动服务满足乘客观看多场赛事活动的出行需求.为乘客减少了出行决策难度与长时候车、车上无座等问题.同时作为公共交通系统的补充，提高了公共交通服务水平和应对灵活观赛出行需求的适应能力.

2)针对观赛人群单比赛日内为观看多场赛事活动而在比赛场馆间产生的出行需求，本文基于对多出行需求、混合搭载和带有时间窗和载量约束的考虑，以最小化赛事公交使用、开行成本为目标构建了赛事公交车辆路径优化模型.

3)求解算法中利用两种有效不等式，提高57.3%的精确求解计算效率，采用带阈值的禁忌搜索算法能够在可接受的计算误差范围内，以较高的计算效率得到优化结果.而基于最优时差插入法的遗传算法则能够更好地实现赛事公交车辆路径优化模型求解，相较于基本精确求解计算效率能够提升99.4%，并可得到不同规模条件下算例的车辆路径优化方案，以期为推动2022年北京冬季奥运会交通发展提供规划参考.