窗口伸缩优化的同步压缩算法及其在变转速工况瞬时频率估计上的应用

吴红安 吕 勇 易灿灿 袁 锐

1.武汉科技大学冶金装备及其控制教育部重点实验室，武汉，4300812.武汉科技大学机械传动与制造工程湖北省重点实验室，武汉，430081

0 引言

非平稳信号广泛存在于自然界和人类社会生活中，如机械振动信号、通信信号、生物信号等都属于典型的非平稳信号。传统的时频域分析方法难以兼顾信号在时频域的局部化特征，不能有效分析非平稳信号[1]。所以既能反映信号频率随时间的变化规律，又可以描述频域能量信息的时频分析方法[2-3]成为分析非平稳信号的有效工具，诸如短时傅里叶变换(short-time Fourier transform，STFT)、连续小波变换(continuous wavelet transform，CWT)、魏格纳-威利分布(Vigner-Ville distribution，WVD)等时频分析方法已被广泛应用[4]。STFT与CWT受海森伯格不确定性原则的限制，无法在频率与时间方向同时获得最佳分辨率，因此无法产生能量集中的时频表示(time-frequency representation，TFR)；WVD利用信号的自相关函数进行时频变换，在很大程度上提高了时频表示的频率分辨率，但这只针对于处理单分量信号，当处理多分量信号时，会不可避免地产生交叉项干扰。时频重排(reassignment method，RM)[5-6]通过调整时频平面的能量定位来提高时频表示的聚集性和可读性，但却无法进行信号重构。

DAUBECHIES等[7]提出了一种类似于时频重排的同步压缩小波变换(synchrosqueezing transform，SST)方法，在CWT的基础上，对变换后的小波系数进行重排，在提高信号时频分辨率的同时很好地保持了信号重构的特性。类似地，基于STFT的同步压缩(SST-based STFT，FSST)[8]也可以提高时频聚集性并支持可逆重构，但是同步压缩本质上是基于信号由纯谐波叠加的假设，因此只适用于处理平稳或缓变信号，对于频率快速变化的信号，其时频表示的能量仍会在一定范围内发散,导致在时间方向上的能量模糊问题依然严重。

基于SST、FSST等的时频分析方法存在抗噪性差、仅对谐波信号有较好的时频聚集性等问题[9-10]，目前关于时频同步压缩的研究主要有时频聚集性的提高，瞬频估计精度的提高，针对多分量、变工况、强调频信号分析的时频分辨率的提高等[11-13]。陈向民等[14]基于自适应时频滤波提取变转速齿轮故障特征来提高瞬时故障特征估计效果；YU等[15-18]先后提出了同步提取变换、多重同步压缩变换等方法，不断提高时频聚集性。尽管这些方法均在一定程度上提高了时频分辨率，但也都延续了STFT固有的带宽大、能量发散等缺陷[17]。OBERLIN等[19]、PHAM等[20]进一步提出了高阶同步压缩变换方法，在SST的前提下进一步将频率轴细分，从而提取更加锐化的时频脊线，得到了更精确的瞬频估计模型。

针对现有的STFT、SST和FSST等时频方法窗口参数固定、抗噪性能差、分析非平稳调频信号时无法为轴承故障诊断提供足够准确的信息等问题，本文依据信号的可分性，针对频率快速变化的非平稳信号，提出一种窗口伸缩优化同步压缩短时傅里叶变换(SST-based STFT for window extension and compression optimization，WECOFSST)算法，并推广至二阶和高阶的时频变换。

1 基于短时傅里叶的时频同步压缩变换

短时傅里叶变换是用一个时频局部化的固定窗函数来截取信号序列，然后进行一系列加窗数据帧的快速傅里叶变换来处理信号的时频分析方法，通过窗口随时间“滑动”表示信号任意时刻的频谱特征。为便于分析非平稳信号s(t)，可将其等效为有限个具有时变幅值和时变或固定频率的分量信号的线性组合，设信号模型如下：

(1)

m式中，Ak(t)为信号各分量的瞬时幅值，且Ak(t)>0；φk(t)表示瞬时频率的相位函数，且φk(t)>0；K为分量个数且为有限值。

信号s(t)的STFT为

(2)

式中，τ为信号的时移;g(τ-t)为时移窗函数。

(3)

式中，ωx(t,η)为相位时移函数，瞬时频率估计Fx(t,η)=Re(ωx(t,η))。

FSST就是在时频域将变换系数X(t,η)按照(t,η)→(t,ωx(t,η))的映射关系对频率变量进行压缩重排，表达式如下：

(4)

式中，δ(ωx(t,η)-α)为频率重心压缩重排函数，δ为狄拉克函数。

图1给出了时刻t下频率点η到α的映射过程，即对频率点压缩重排，遍历所有时刻，所得结果就是FSST的结果。

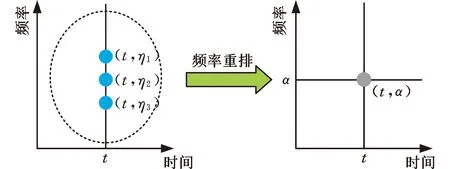
图1 FSST中时刻t下的频率分配过程示意图Fig.1 Schematic diagram of the frequency allocationprocess at time t in FSST

2 窗口伸缩优化的时频同步压缩算法

2.1 窗口伸缩优化的STFT和FSST

传统的STFT时频窗宽是固定不变的，使得其获得的时频图能量聚集性差、脊线模糊、时频分辨率低，导致时频分析效果较差。但是常见工程信号的瞬时频率并非平稳变化，尤其是当非平稳多分量信号的各个分量比较接近时，很难确定一个固定的窗口参数使得全局的FSST时频效果很好。

由不确定性原理可知，对于给定信号，如果能量有限，则它对应的时宽与带宽乘积等于常数，满足以下关系：

(5)

式中，Δt、Δf分别为时间和频率分辨率，若信号为Gauss信号，则等式成立。

不确定性原理表明，信号的时宽与带宽不能同时趋于无限小，时频分辨率相互制约，所以时频分析应依据不同信号选定不同的时窗函数来分析信号的局部特性[11]。本文选用Gauss窗函数来进行实验和分析。

考虑单一频率信号y(t)=Aei2πmt，其中，m为常数。对y(t)进行窗口伸缩优化的STFT如下：

(6)

式中，σ(t)为t的函数，用YT-STFT(t,η,σ(t))表示时变伸缩窗口σ参数下信号y(t)的STFT。

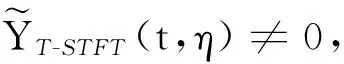
(7)

综上所述，对于一般信号s(t)，根据式(7)估计信号瞬时频率函数ωs(t,η)，即

(8)

ST-STFT(t,η,σ(t))≠0

所以，信号s(t)的窗口伸缩优化同步压缩短时傅里叶变换(SST-based STFT for window extension and compression optimization，WECOFSST)定义为

δ(ωs(t,η,σ(t))-ξ)dη

(9)

如果g(·)为Gauss函数，则式(8)中右侧第一项为零，信号瞬时频率估计函数为

(10)

ST-STFT(t,η,σ(t))≠0

2.2 二阶和高阶的窗口伸缩优化的STFT和FSST

FSST仅适用于分析由缓变纯谐波组成的信号，在分析频率快变信号时，分辨率会大幅降低，时频脊线变得模糊。为弥补这个缺陷，研究更精确的瞬频估计的二阶同步压缩变换，通过线性调频模型来进行信号瞬频的精确估计，类似于重新定义了同步压缩中的相变换算子。

二阶FSST首先定义一个二阶局部调制系数qt,x(t,f)：

(11)

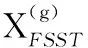
即调制系数qt,x(t,f)是FSST瞬频估计关于时间t的一阶导数,所以二阶的瞬时频率估计为

(12)

则信号s(t)的二阶同步压缩变换如下：

(13)

高阶的同步压缩变换方法(FSST-N)基于信号的幅值与相位的泰勒展开，定义新的瞬时频率估计为

(14)

类似于FSST-2，FSST-N的表达式为

XFSST-N(t,ω)=

(15)

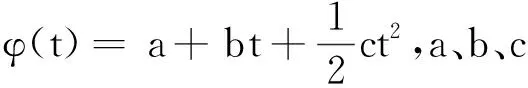
(16)

SWECOFSST-2(t,ω,σ(t))=

(17)

类似于SWECOFSST-2(t,ω,σ(t))，N阶窗口伸缩优化的FSST的表达式为

SWECOFSST-N(t,ω,σ(t))=

(18)

2.3 窗口伸缩优化确定最优窗口参数

对于任意给定的一个信号，如果能确定一个时变窗口参数σ(t)，它可以比较清晰地反映出信号局部信息，那么就可通过最优窗宽的FSST获得较好的时频分布，以确定更精确的瞬时频率，但是实际信号并没有任何已知的先验信息，所以需要对适合信号时变特性的窗口参数σ(t)进行伸缩优化并确定。

信息熵是用来度量信息不确定性的一个函数[11,13]。本文通过使用信息熵值大小来评判局部时刻的最优窗宽。当信号时变平稳，则伸长对应窗宽，以加大信号数据量，提高频率分辨率；当信号时变非平稳，则压缩对应窗宽，提高时间分辨率，从而有效反映信号的突变情况。所以，按照信号的局部特性进行合适截取，以最小信息熵准则计算截取的各段信号的最优窗宽，能够有效提高信号的时频分辨率。

根据信号时频分布和概率的相似性，各窗内信号的概率分布如下：

(19)

则对应的信息熵为

(20)

依据最小信息熵准则，该时刻对应的最佳窗长可计算如下：

σbest=argmin(Hs(σ))

(21)

运用局部最小信息熵，估计各个时刻的最优窗口参数σ的流程如图2所示。

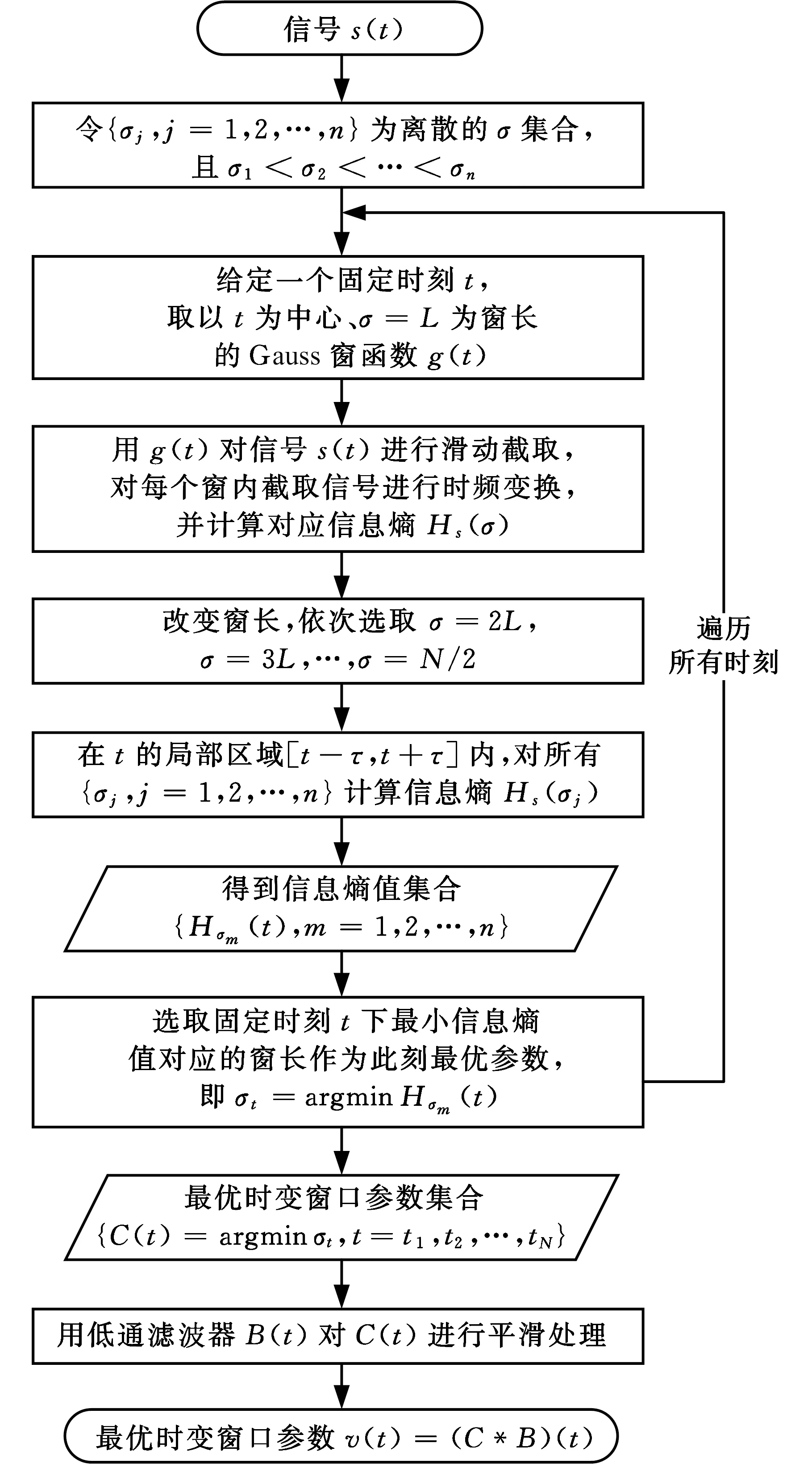
图2 基于最小信息熵准则进行窗口伸缩优化的时变参数估计流程示意图Fig.2 Process diagram of time-varying parameterestimation process based on minimum informationentropy criterion for window extension andcompression optimization

3 数值仿真

3.1 合成信号仿真

为了说明提出的方法在处理非平稳信号上的优势，建立了一个具有不同的调幅-调频规律的两个分量信号组成的多分量信号:

s(t)=s1(t)+s2(t)+n(t)

(22)

(23)

其中，n(t)是信噪比为3 dB的Gauss白噪声。取采样频率100 Hz，采样时间4 s，则多分量信号的瞬时频率为

(24)

由图3可以看出，信号分量s2比s1具有更强的调频特性。

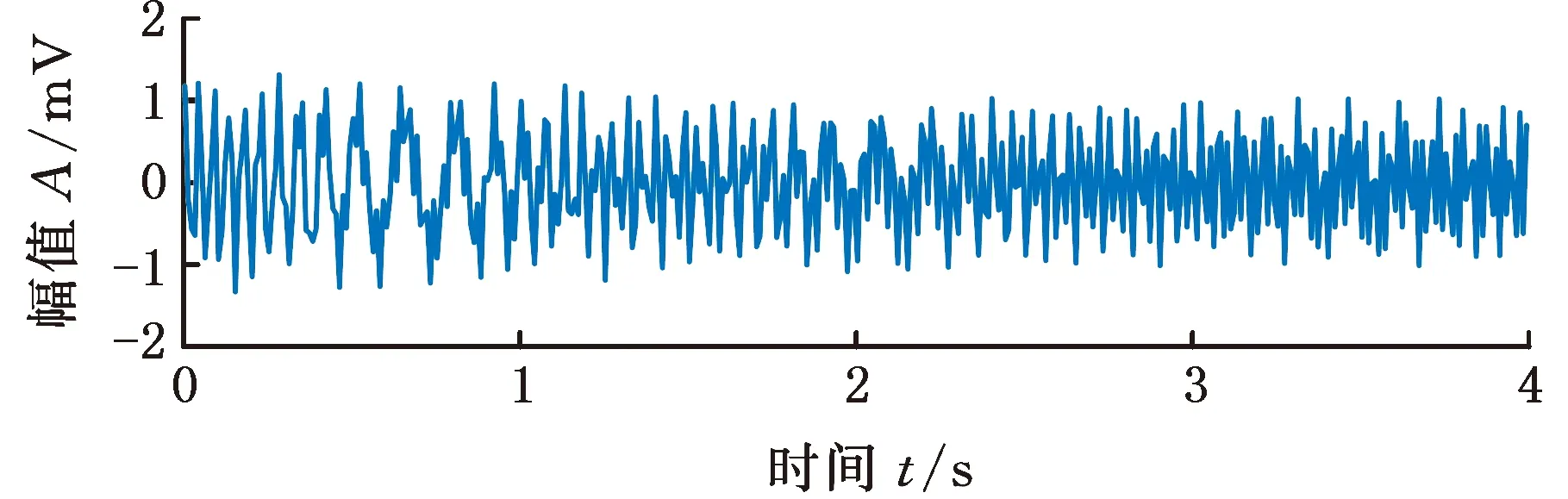
(a)信号s

理想的时频表示应该高度集中在瞬时频率轨迹上，即在每个时间点上只出现一个频点在时频平面上，以描述这种单组分模式。图4a、图4b中STFT时频带宽较大，时频谱图的能量发散在瞬时频率轨迹周围，并在瞬时频率中心位置达到最大值，而这正是由STFT的固定窗宽导致的，STFT具有较差的时频分辨率。RM和FSST方法产生的时频结果如图4c～图4h所示，RM、FSST和二阶FSST(FSST-2)三种方法均显示出比STFT频谱图能量更加集中的结果。从放大视图中可以看出，对于分量s1的时频描述，RM、FSST和FSST-2反映了相似的集中时频表示。但对于强调频信号分量s2，FSST方法能量发散严重，RM和二阶FSST能生成较为紧凑的时频描述，但能量仍会散布在一定范围内，且RM在频率峰值变化处能量发散现象较二阶FSST更严重。

(a)STFT时频图(b)STFT时频图局部放大

该仿真信号通过本文提出的窗口伸缩优化方法(WECOFSST)进行处理，结果如图5a～图5d所示。对比图4局部放大的时频图可以清晰地观察到：RM、FSST和二阶FSST在描述强调频的非平稳信号时频分布时均会存在不同程度的能量发散现象，FSST在信号频率快变区间，能量聚集性较差，RM和FSST-2虽能更准确地描述信号的调频时变规律，但仍存在一定的能量发散现象，时频脊线模糊，无法精确估计瞬时频率。鉴于固定窗口分辨率单一、难以反映信号局部特性的缺陷，本文提出的基于窗口伸缩优化的FSST(WECOFSST)和二阶WECOFSST方法WECOFSST-2通过伸缩优化时变窗口来适应信号的局部变化，使得信号在频率变化慢的时刻具有宽的时窗，在频率变化快的时候具有窄的时窗，从而提高信号的时频分辨率，得到更好的时频分布。WECOFSST和二阶WECOFSST结果显示出比RM、FSST、二阶FSST结果更加能量集中的时频表示，如图5所示。对比观察图5b、图5d可以发现，WECOFSST-2在描述强调频信号时频分布时的能量脊线比WECOFSST更加集中、更加清晰。由图5e、图5f可以发现，二阶WECOFSST提取出的瞬频与实际瞬频曲线高度重合，瞬时频率估计结果精确度较高。

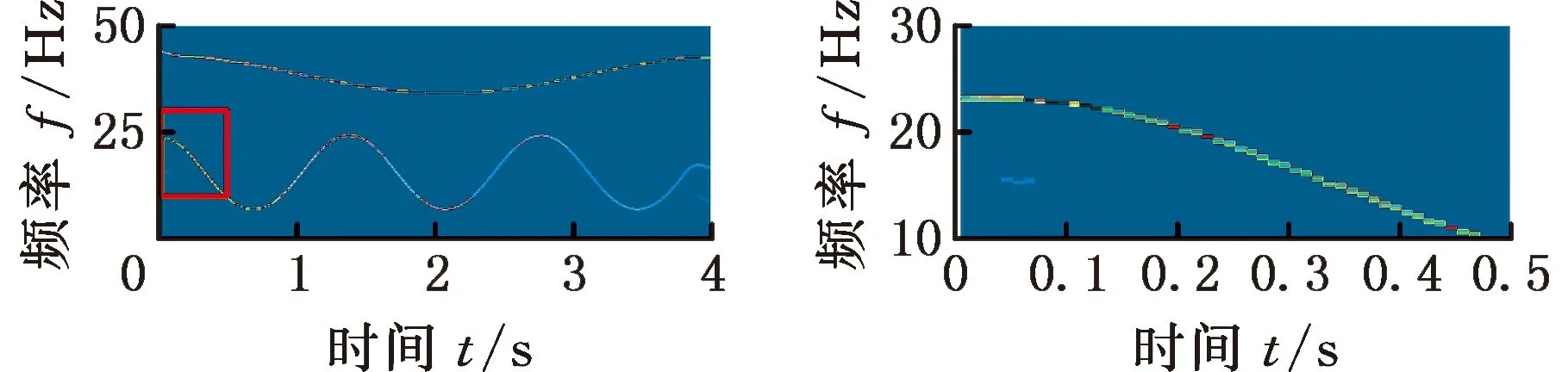
(a) WECOFSST时频图(b) WECOFSST时频图局部放大

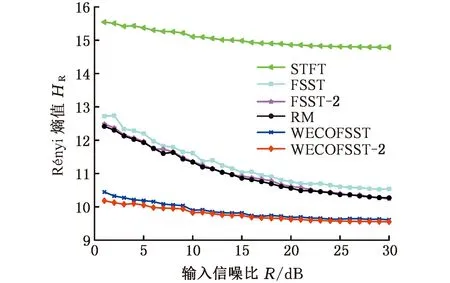
图6 不同时频分析方法下的Rényi熵Fig.6 Rényi entropy under different time-frequencyanalysis methods

为了客观地比较每个结果，使用Rényi熵来定量评估不同方法的性能，Rényi熵值越小表示时频表示越集中。如图6所示，Rényi熵曲线表明，WECOFSST和二阶WECOFSST结果比RM、FSST及二阶FSST结果显示出更集中的时频表示。当信噪比为10时，相应的Rényi熵分别为15.11(STFT)、11.61(FSST)、11.34(RM)、11.33(FSST-2)、9.899(WECOFSST)和9.824(WECOFSST-2)。显然，在上述时频分析方法中，窗口伸缩优化的二阶FSST(WECOFSST-2)针对瞬时频率快速变化的信号时频描述效果最好，能量集中度最高。

3.2 时变转速工况下行星齿轮箱太阳轮故障信号仿真

在本小节中，首先对变转速工况下行星齿轮箱故障信号进行仿真分析，验证所提方法提取敏感共振频带内故障特征频率的有效性。

为模拟太阳轮故障，建立信号模型[21]如下：

(25)

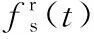
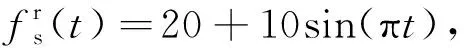
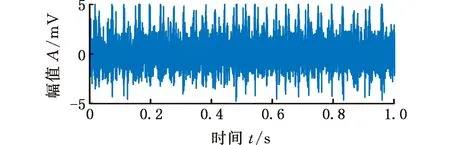
(a)信号的时域波形

太阳轮故障仿真信号的分析结果如图8a～图8d所示。可以清晰地观察到，STFT时频图能量集中效果较差，仅能大致描述出信号的瞬频变化趋势，时频分辨率低，时变故障特征难以提取；RM和FSST时频图虽获得了较为清晰的瞬时频率变化趋势，但是由于边频带成分密集，在瞬频快变区间内，沿时间方向能量依然比较模糊，如图8b、图8c、图8d中标记的红色区域内存在部分混叠现象，影响故障特征识别，所以上述方法难以精准识别密集分布的时变边频带。

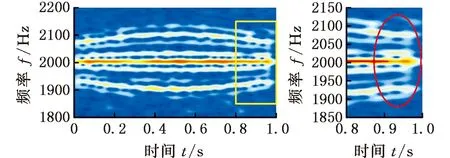
(a)STFT时频分布图及局部放大图

图9a、图9b所示时频图为本文所提方法WECOFSST和WECOFSST-2方法分析的变转速工况下行星齿轮箱模拟太阳轮故障的仿真信号时频表示。与FSST相比，WECOFSST和WECOFSST-2使用了更加精确的瞬时频率估计公式，进一步细分了频率轴，与图8对比可以发现，WECOFSST和WECOFSST-2能更有效地提取快变信号的瞬时频率特性，显著提高时频分辨率，使得时频面脊线能量更加锐化集中，各个瞬时频率变化曲线更加清晰，充分展示了算法的优越性。

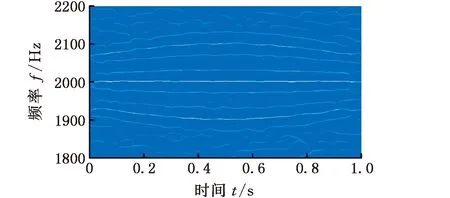
(a)WECOFSST时频分布

4 实验仿真分析

4.1 实测蝙蝠信号仿真

针对非平稳多分量信号，通过引用美国伊利诺伊大学Beckman实测的大棕色蝙蝠发出的数字化回声定位脉冲信号[22]来验证所提方法在蝙蝠信号中的分析效果。蝙蝠通过产生调频和向下扫频信号，并借助声波的反弹来实现回声定位识别。该信号包括400个采样点，采样频率为143 kHz，采样时间间隔为7 μs。为了验证本文所提方法的有效性，对比STFT、FSST和FSST-2分析结果，如图10所示。蝙蝠回波信号实际上是一个多分量信号，它包含了四个能量与持续时间均不同的非线性调频信号分量。

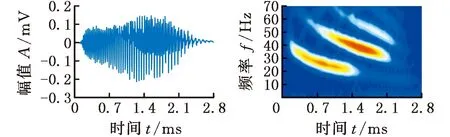
(a)时域波形(b)STFT时频分布

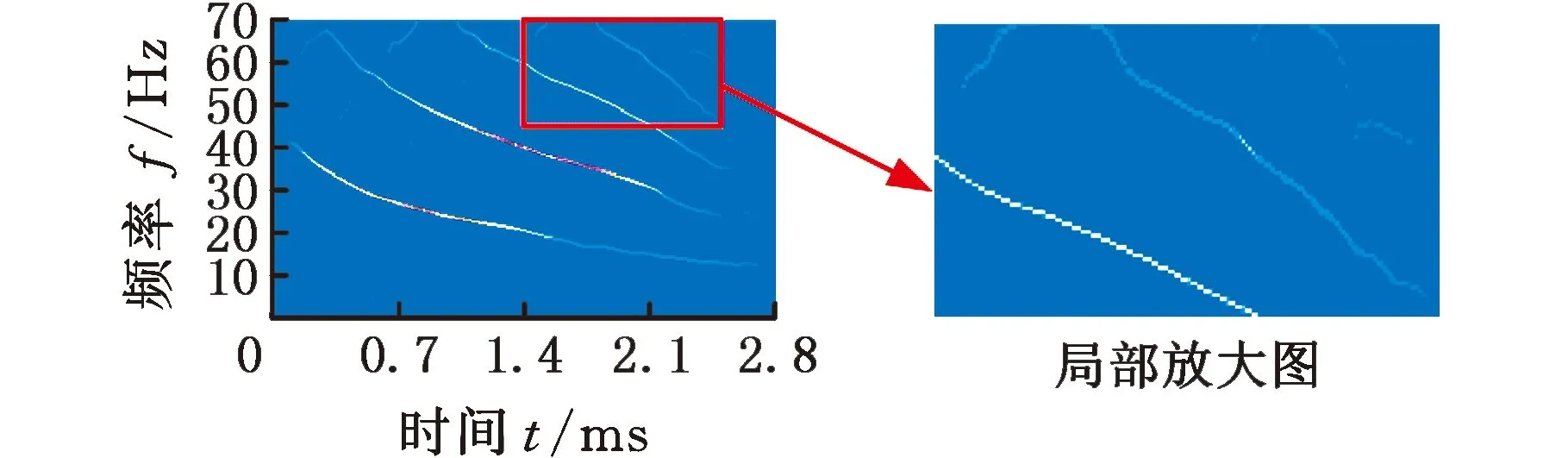
(a)WECOFSST时频分布

图11所示为由WECOFSST和WECOFSST-2得到的时频分析结果。对比图10可以发现，STFT有着最差的频率分辨率，FSST和FSST-2方法得到的时频分布虽然具有较高的能量集中度，但仅限于前三个分量，第四个分量(高频分量)几乎无法被描述(对比图10、图11红色标记框)。相较而言，本文所提方法根据信号时变特性伸缩优化窗宽得到了频率带宽更小、能量集中度更高的时频表示，且WECOFSST-2时频图能量聚集性最高。WECOFSST和WECOFSST-2在FSST和FSST-2的基础上不仅有能量聚集性更高的时频表示，同时还可以清晰地表示出蝙蝠信号的高频分量。

4.2 实验信号分析

本文以电机启停运转过程来模拟实际变转速工况，实验装置如图12所示，主要由控制台、伺服电机、齿轮变速箱(减速比Z1∶Z2=16∶24)、磁粉制动器和外置轴承座组成，加速度传感器安装在外置轴承座上。外置轴承座内安装深沟球轴承作为振动信号测试对象，轴承型号为6202，其具体参数如表1所示。

(a)实验台实物图

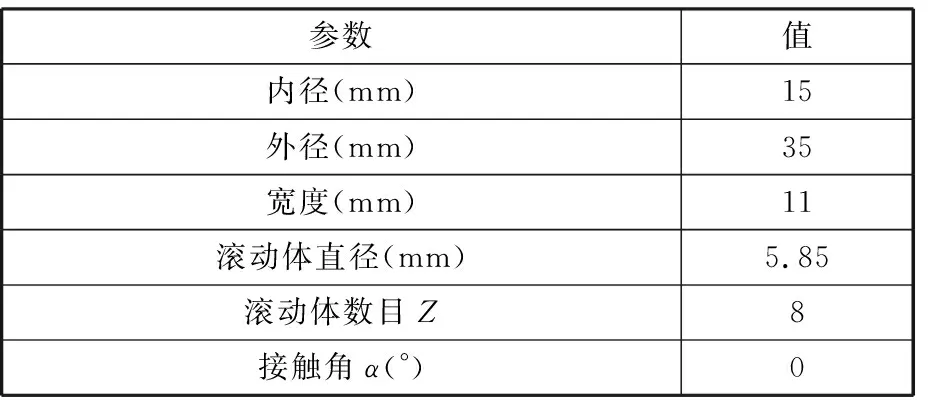
表1 故障轴承的几何参数

在实验中设置伺服电机运行工况为“加速启动—平稳运行—减速停机”，电机启动后转速呈线性增大至1500 r/min，然后开始线性降低至停止运行。设置信号采样频率为512 Hz，采样时间为11 s。振动加速度传感器测得的时域信号和频谱如图13所示。

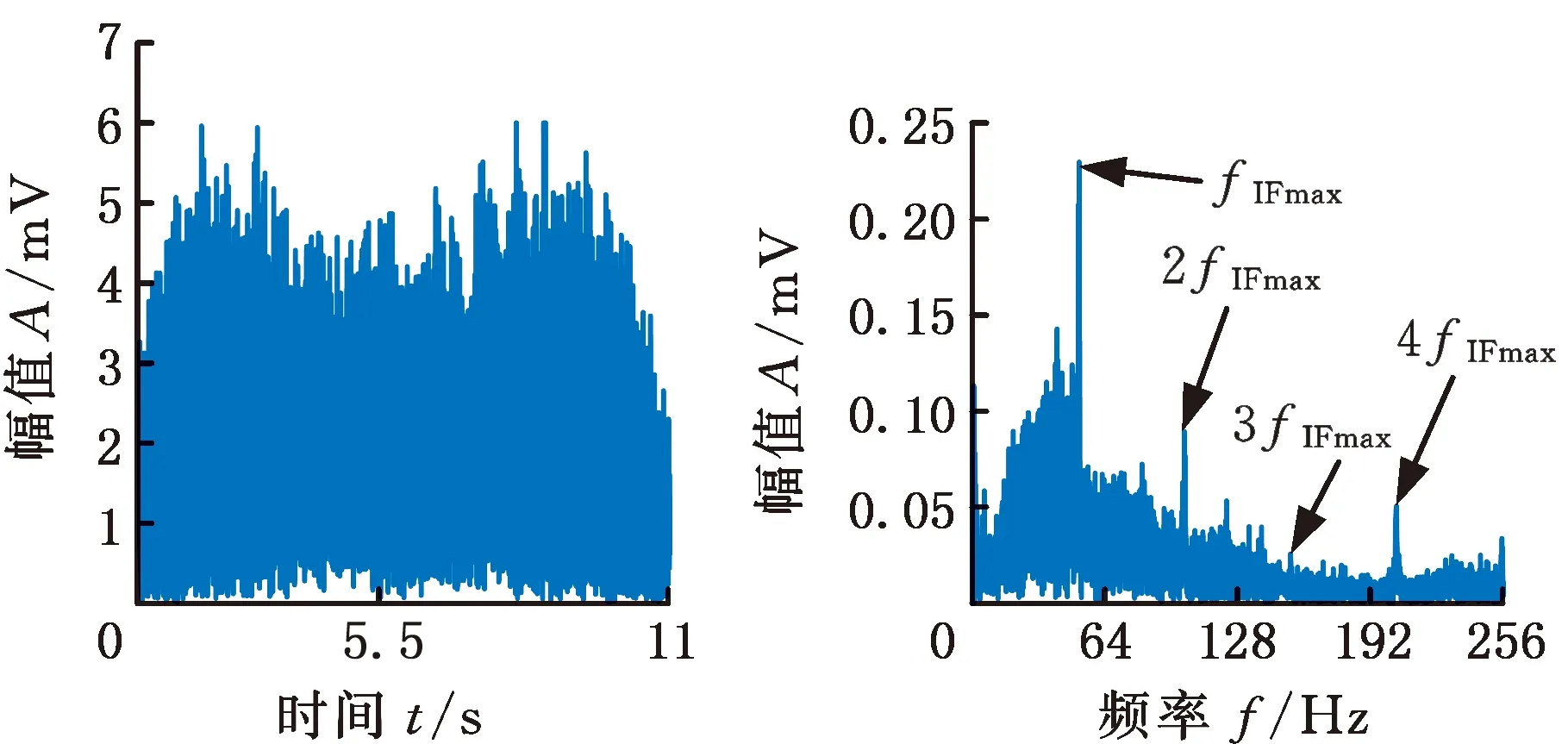
图13 实验采集的信号的时域波形和频谱Fig.13 Signals collected in the experiment

由于故障所在轴转速随时间变化，传统的包络分析无法为准确的轴承故障诊断提供足够的信息，因此分别使用STFT、RM、FSST、FSST以及WECOFSST和WECOFSST-2这六种方法对该信号的幅值包络进行时频分析，解调出瞬时故障特征频率，以验证所提出方法的有效性及相对其他同类方法的优越性。

图14所示为STFT、RM、FSST、FSST-2四种方法时频表示及其提取到的瞬时故障特征频率fIF及其倍频曲线。从图14中可以观察到：在时频表示上，使用STFT和RM仅能粗略地识别出瞬时故障特征频率，尤其是STFT在能量集中方面效果很差，难以准确识别瞬时频率；FSST和FSST-2相较于STFT，无论是在能量集中方面还是在平面清晰度等方面均优于STFT方法，结合峰值搜寻算法可以较为准确地提取出瞬时故障特征频率，但是在识别瞬时故障特征频率的二倍频、三倍频时误差较大，精度较低。

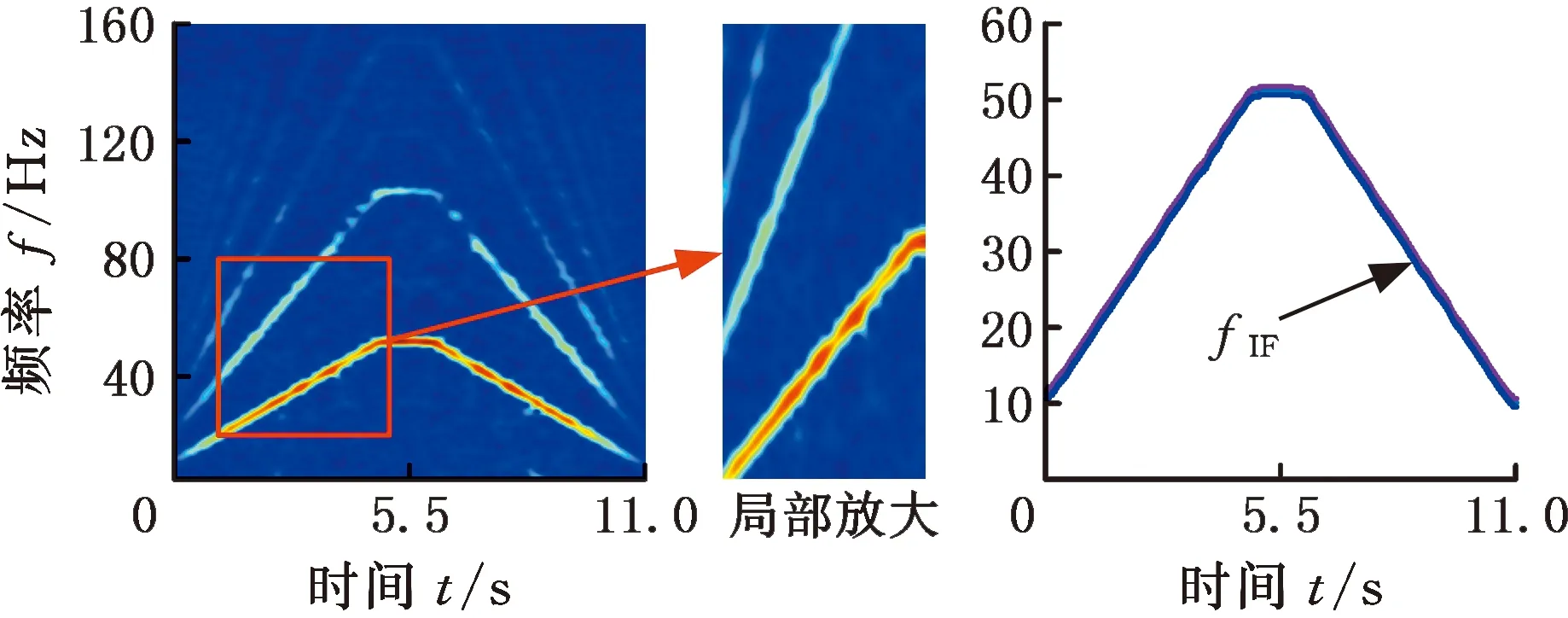
(a)STFT时频图(b)STFT时频脊线提取

图15为本文提出的新的窗口伸缩优化方法WECOFSST和WECOFSST-2时频表示及其提取到的瞬时故障频率及其倍频曲线。从图15中可以清晰地发现，窗口伸缩优化后的方法结合峰值搜寻算法能够较为准确地提取出瞬时故障特征频率及其二倍频、三倍频曲线，且精度较高，符合理论公式估算结果。

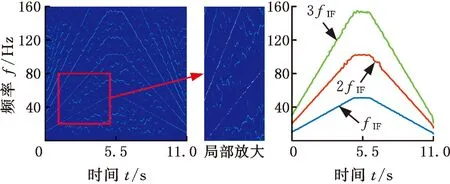
(a)WECOFSST时频图(b)WECOFSST时频脊线提取

分别计算STFT、RM、FSST、FSST-2以及WECOFSST和WECOFSST-2六种方法在输入信噪比R=20时的Rényi熵值，如表2所示。可以发现WECOFSST和WECOFSST-2方法的Rényi熵值较其他方法的Rényi熵值更小，其中WECOFSST-2方法Rényi熵值最小，表明本文所提新方法的瞬时频率估计更加精确。综合对比图14和图15可以发现，窗口伸缩优化方法在频率缓变时刻伸长时窗来截取信号，在频率快变时刻压缩时窗来截取信号，可以提高信号的时频分辨率，得到更好的时频分布，提取的时频脊线较FSST方法时频脊线更加清晰准确，该方法无论是在能量集中还是在时频平面清晰度方面均优于STFT、RM、FSST和FSST-2方法，充分验证了算法的可靠性和有效性。

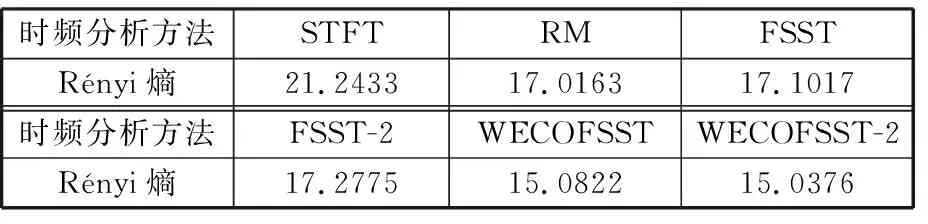
表2 不同时频分析方法在信噪比R=20时Rényi熵值

5 结论

(1)本文在同步压缩变换的基础上，考虑时变非平稳信号的局部变化特性，将提出的窗口伸缩优化短时傅里叶变换应用于同步压缩理论中，得到新的窗口伸缩优化的同步压缩短时傅里叶变换方法，并应用于变转速工况瞬时故障特征频率的识别提取，提出的方法可以优化窗口参数，较好地反映信号的局部特性，增强信号在局部和全局的能量聚集效果。

(2)算法通过窗口伸缩优化来高效匹配信号的时变特征，利用最小信息熵值确定最优时变窗口参数，使信号在任意时刻都具有最优的时频分辨率和较高的鲁棒性，在时频表示的清晰度上与现有方法相比具有较大的优势。

(3)该方法应用在旋转机械变转速工况瞬时频率估计上，适用于处理非平稳的多分量信号，相较于其他方法，能获得较高精度的估计结果，且具有较高的可靠性。