基于卷积神经网络的超声图像散斑去噪算法

廖丽丽，张东

武汉大学物理科学与技术学院，湖北武汉 430072

前言

超声图像技术因实时性高、安全性强、费用低等特点，在临床医学诊断中有着广泛的应用。在超声成像设备中，超声波声束经过反射、吸收、连续散射等物理过程后，可以通过检测反向散射信号来获得所需成像介质的结构信息。超声成像是一种相干成像的过程，人体组织可以看作是散射体的集合，多个散射体占据一个分辨单元，这些散射体会以随机相位和振幅散射小波，从而引发回波信号的随机波动，形成散斑噪声，导致不易准确地分辨超声图像中的各种组织结构信息。这些散斑噪声常常会对医师进行后续诊断造成不良影响，例如在使用HIFU 超声导航技术对肿瘤进行实时消融治疗时，散斑噪声的存在会影响临床医师对肿瘤位置的精准判断，当定位不准确时，会损害患者的正常组织，对患者的病情十分不利。因此，研究如何通过抑制散斑噪声来提高超声图像的质量十分重要。

传统的超声图像去噪算法主要有非局部均值滤波类算法（NLM、OBNLM）［1-2］、散斑抑制各向异性扩散滤波（SRAD）［3］、三维块匹配（BM3D）［4］等算法，尽管这些算法能够有效地消除散斑噪声，但往往不可避免地会造成超声图像中纹理信息的损失以及过度平滑的边缘，对超声诊断产生不良的影响［5］。因此，超声图像去噪算法的研究重点是如何在消除散斑噪声的同时，尽可能地保留图像纹理信息，减少模糊，增强边缘。

随着硬件计算能力的提升，神经网络强大的学习和拟合能力在图像处理中展露出巨大的潜力，例如，卷积神经网络（CNN）［6］目前已被应用于图像分类、目标检测、图像分割、图像去噪等多个领域。目前，已有许多学者利用卷积神经网络对低剂量CT 图像［7-8］、OCT 图像［9］、MRI 图像［10］等医学图像进行去噪，并获得了较好的效果，这启发我们使用基于卷积神经网络的去噪模型来抑制超声图像的散斑噪声，提升超声图像的图像质量。

本文通过模拟超声成像的过程来生成含有散斑噪声的图像及其对应的无噪声图像作为训练数据，利用卷积神经网络及改进的损失函数建立超声图像散斑去噪模型DSCNN（De-speckling CNN），从而有效地消除散斑噪声，并最大化地保留了纹理信息和清晰的边缘。

1 超声图像相关理论

1.1 散斑噪声模型

在许多超声图像去噪算法中，散斑噪声被简单地假定为乘性噪声，然而这并不完全符合散斑噪声的实际特性，因此，我们采用模拟超声成像过程的方式来合成散斑噪声，以获得更加符合真实超声图像数据分布的训练集。

超声成像是一种相干成像模式，具有随机相位和振幅的回声相互叠加，产生复杂的斑点状干涉图像，称为散斑噪声。超声成像的过程中，散斑噪声的产生无法避免，将单位分辨单元内的散射体数量记作散射体密度，根据散射体密度的不同，通常可将散斑噪声分为两种类型，完全发育的散斑噪声和不完全发育的散斑噪声，完全发育的散斑噪声的包络检波图像服从Ralyleigh 分布，不完全发育的散斑噪声的包络检波图则基本服从Nakagami分布［11］。本文将使用Perreault提出的散斑噪声模型［12］在高质量的CT图像上合成散斑噪声，从而获得大量的更贴合真实分布的模拟超声图像及配对的无散斑噪声的图像作为去噪模型的训练数据，达到数据增强的目的。

1.2 模拟超声成像技术

常见的数字B型超声成像系统，通过使用超声声束照射人体组织，采集反射的信号数据，再对信号进行处理与分析，从而得到体内组织器官的灰度图像［13］。本文使用基于卷积神经网络的深度学习去噪模型来抑制散斑噪声，这是一种监督学习的方式，因此，需要获得大量的含散斑噪声与不含散斑噪声的成对训练数据。首先，由于在临床上不可能直接获得超声图像对应的无噪声图像，所以本文通过在高质量的CT 数据集上合成散斑噪声来获得模拟的超声图像（含有散斑噪声），同时，我们将相应的无散斑噪声的CT 图像作为对应的标签图像，从而得到充足的成对训练数据以训练出针对超声图像散斑噪声的去噪模型。其次，在不同的超声成像设备或人体内部环境中形成的散斑噪声强度大小不尽相同，因此，利用模拟超声成像算法，仅通过修改算法参数就可以获得含不同强度散斑噪声的模拟超声图像，实际应用的过程中，这种数据增强的手段使得我们训练得到的去噪模型具有更强的泛化性能和鲁棒性，能够适应不同的超声成像设备或人体内环境。

Perreault 提出的基于超声图像采集模型和散斑噪声形成模型的模拟超声成像算法主要可以分为3个步骤：第一步，对像素网格进行采样以此来模拟超声束的扇区扫描；第二步，将散斑噪声添加到采样像素；第三步，通过插值填充采样所引起的空白。通过这种方式合成的含有散斑噪声的超声图像，无论是在视觉上还是理论上都非常接近B型超声图像。

2 超声图像去噪模型DSCNN

在本文提出的超声图像散斑去噪模型DSCNN中，我们使用x∈Rm×n表示具有散斑噪声的超声图像，用y∈Rm×n表示相应的无散斑噪声图像，DSCNN的学习目标即是实现x到y的端到端映射。

2.1 网络结构

图1展示了本文所提出的DSCNN网络结构示意图，其中，输入是模拟的超声图像，输出是经DSCNN去噪处理后得到的结果图。这是一个9 层的卷积神经网络，前8层均含有64个卷积核，而最后1层仅含1个卷积核。通过计算感受野的尺寸，我们可以知道，步长为1 时，一个3×3 的卷积核经过3 层卷积操作与一个7×7 的卷积核进行一次卷积操作的感受野大小相同，这意味着小尺寸（如3×3）卷积核通过多层卷积操作可以得到与大尺寸（如7×7）卷积核同等规模的感受野，除此之外，小尺寸卷积核的多层卷积操作可以增加网络深度，提高网络的非线性拟合能力［14］；其次，在感受野大小相同的情况下，使用更多的小尺寸卷积核而不是大尺寸卷积核，能够大大减少网络的参数数量，提高神经网络的收敛速度。因此，在整个DSCNN 的网络结构中，我们都采用3×3 的小尺寸卷积核。同时，在DSCNN 的网络结构中，每一层都采用零填充的方式（Zero-padding）来保证每层输出的特征图尺寸不变。此外，每个卷积（Conv）层之后都跟着ReLU 层作为激活函数，并且7 个中间层每层都在卷积操作和激活函数后使用批归一化（BN 层），BN层的作用是能够加快神经网络的收敛，避免梯度消失或梯度爆炸的发生［15］。

图1 DSCNN网络结构Figure 1 Structure of de-speckling convolutional neural network

2.2 损失函数

大多数基于深度学习的图像去噪算法都是使用l2或均方误差（MSE）损失函数，最小化l2损失函数与最大化峰值信噪比（PSNR）的目标一致，因此，基于l2损失函数的深度学习去噪算法往往能够在PSNR 指标上得到较好的结果，然而PSNR 图像质量评估指标并不与我们人类的真实视觉感受完全一致。当使用l2（或者MSE）作为损失函数时，实际是潜在地假设我们采集到的样本都来自同一个高斯分布［16］，但真实的图像样本并不满足高斯分布，这也就意味着我们在使用一个单峰的高斯分布去强行拟合一个多模态的图像数据分布，从而不可避免地会在去除散斑噪声的过程中导致纹理细节的模糊以及边缘的过度平滑。因此，使用l2作为损失函数的深度学习类超声图像去噪算法往往都存在着较为严重的纹理细节丢失问题，这对专业医师进行后续的肿瘤检测、分割等操作都会产生不良的影响。相反，基于l1损失函数的深度学习模型能够得到边缘相对更清晰的图像。l1损失函数计算的是模型预测值f(x) 与真实值y之间的平均距离，其定义及梯度计算公式如下所示：

其中，xi是输入x的分块，yi是真实值y相应位置的分块，其中d=f(xi)-yi。从l1损失函数的定义（1）及其梯度计算式（2）可以看出，对于使得d= 0 之外的任何输入，其梯度的绝对值都相同，较为稳定的梯度意味着它对异常数据不敏感，不易产生梯度爆炸的问题，模型训练的过程更为稳健，但这样的特性也意味着即使到d值极小的最后阶段，仍保持着绝对值为1的梯度，这将导致模型收敛困难，除此之外，l1损失函数在d= 0 处不可导也是一个不可忽视的缺点。基于此，我们在DSCNN 中使用smoothl1损失函数［17］，其巧妙地规避了传统的l1损失函数的缺陷，保留了l1损失函数的优势，smoothl1损失函数的定义及其梯度计算公式如下所示：

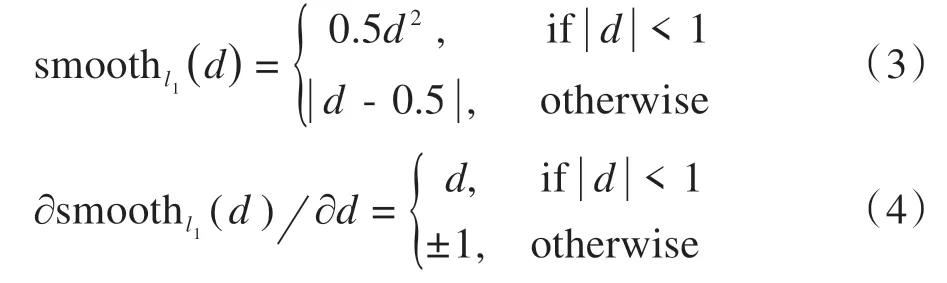
从式（4）中可以看出，smoothl1损失函数在任意点都可导，同时在d值较小时，其相应的梯度值也足够小。

因此，在不增加模型复杂度、影响实时性能的条件下提出一种低成本的解决方案，即使用smoothl1来代替传统的l1和l2作为损失函数，基于此训练出的超声图像散斑去噪模型能够在去噪的同时更好地保留图像细节，减少边缘的过度平滑。

3 实验与结果

本文仿真实验均使用Python3.6编程语言在内存为8 GB 的NVIDIA RTX 2060 GPU 上完成，并使用Tensorflow 1.14训练和测试神经网络。

3.1 实验数据

本文使用的数据来自于公开数据集TCIA［18］，选取1 200张来自40位病人多个部位的CT 图像作为训练集的标签数据，如肺部CT、肝脏CT 等，每张CT 图像的大小为320×320，并利用这些CT 图像生成相应的模拟超声图像。我们在训练DSCNN 的过程中采用分块策略将图像分成64×64的小块，这帮助去噪模型能够达到局部更优解，在去除散斑噪声和保留图像细节上更好地维持平衡，同时，分块的策略也使得训练数据更充足。

3.2 评价标准

PSNR 是研究者们使用最为广泛的图像质量评估标准，值得注意的是，在2.2 小节中我们已经讨论过，基于l2损失函数的去噪模型往往可以在PSNR 这一指标上得到较好的结果，由于PSNR 认为图像信号的保真度与结构性失真无关，因此，图像的视觉效果好坏并非与PSNR 指标的高低完全一致，PSNR 不能作为评估图像质量的绝对标准［19］。相反，结构相似度（SSIM）全面地考虑了非结构性失真（如亮度、对比度等）和结构性失真（如噪声强度、模糊程度等）［20］，这意味着在更注重视觉感知质量的场景下，SSIM 能更加全面、可靠地反映出图像质量的好坏。在本实验中，均值（MEAN）和标准差（SD）这两项图像统计特性也被用于评估图像质量。去噪模型输出数据的MEAN 和SD 值越接近标签数据，就表示超声图像去噪效果越理想，更具体地，SD值的高低标志着图像的灰度分布的离散程度，在接近标签图像SD 值的情况下，SD 值越高，一定程度上表明图像的纹理更清晰。基于上述讨论，我们综合考虑PSNR、SSIM、MEAN、SD这4项指标来评估去噪效果。

3.3 实验结果与分析

为了验证本文提出的DSCNN 能有效地去除超声图像的散斑噪声，以及在保留纹理信息方面具有优势，在实验中将DSCNN 的去噪效果与当下最具代表性的几种超声图像去噪算法进行对比，包括SRAD、NLM、OBNLM、BM3D、基于l2损失函数的卷积神经网络去噪模型（CNN-l2）。在测试实验中，选择400 张模拟超声图像作为测试数据集，经统计，测试数据集的多项指标如表1和表2所示。

表1 不同算法在测试集上的定量表现Table 1 Quantitative results of different algorithms for test set

表2 不同算法在测试集上的统计特性Table 2 Statistical properties of different algorithms for test set

我们选取测试集中的样本数据在图2中展示其测试结果，其中所选取的样本数据的噪声方差σ2=0.2，超声束的数量设置为100，每超声束采样像素点的数量设置为200。图3展示了图2中红色方框内放大后的细节。

通过观察与对比可以发现，CNN-l2虽然能够有效地去除散斑噪声，但同时也造成明显的模糊，影响视觉效果。而从图3可以看到，经过DSCNN 处理后的图像，在去噪效果较好的同时，边缘和纹理也恢复得更为清晰，保留了更多的图像细节，在视觉感知上更为真实，而非局部均值滤波类算法（NLM、OBNLM）在处理抑制散斑噪声与保留边缘、纹理信息的平衡关系时表现出了不足。BM3D 是一种极具竞争力的去噪算法，在应用于超声图像的去噪时，无论是在消除噪声还是在保留纹理细节方面都达到不错的效果。然而，由于BM3D 算法是在变换域中执行滤波操作，这等效于对图像信号进行加窗处理，会引起无法消除的吉布斯效应，这将在BM3D 去噪后的图像上产生划痕状的伪纹理，进而一定程度上影响到后续超声诊断的准确性。SRAD 是一种非线性各向异性扩散滤波算法，由于SRAD算法中假定散斑噪声是一种乘性噪声，因此，在处理基于超声图像采集模型和散斑噪声形成模型的模拟超声成像算法所生成的超声图像时，其表现并不十分理想。

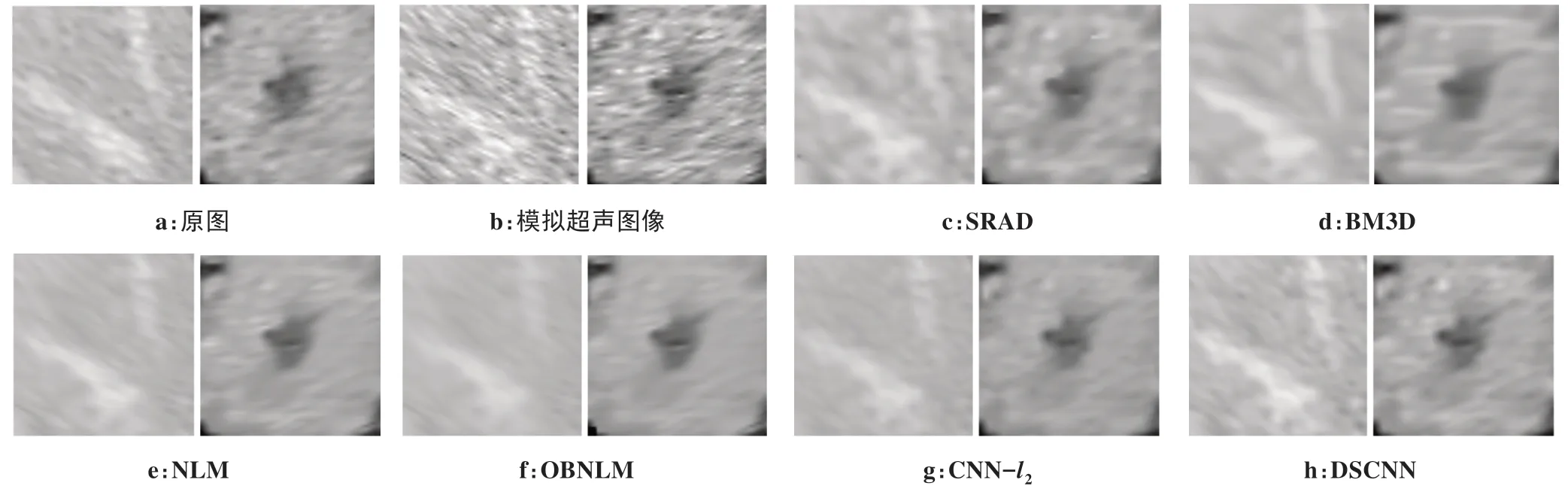
图3 经放大后的图2红色方框区域的细节图Figure 3 A detailed view of the red box in Figure 2 after magnifying

同时，本文在表3和表4中单独列出了图2中测试结果的评价指标。CNN-l2在所有的去噪算法中取得了最高的PSNR 值，这与我们2.2 小节关于PSNR和l2损失函数之间关系的论述一致，但无论是在更全面客观的图像质量评价指标SSIM 上，还是在辅助评价指标MEAN和SD上，DSCNN都表现最好。NLM、OBNLM、SRAD 这3 种算法的各项评价指标较为接近，而BM3D 在所列出的4种传统算法中去噪效果最好。表1、表2中关于测试数据集的整体评价指标也与样本测试数据的结果基本一致。

表3 不同算法在测试集样本数据（图2）上的定量表现Table 3 Quantitative results of different algorithms for sample data in test set(Figure 2 )

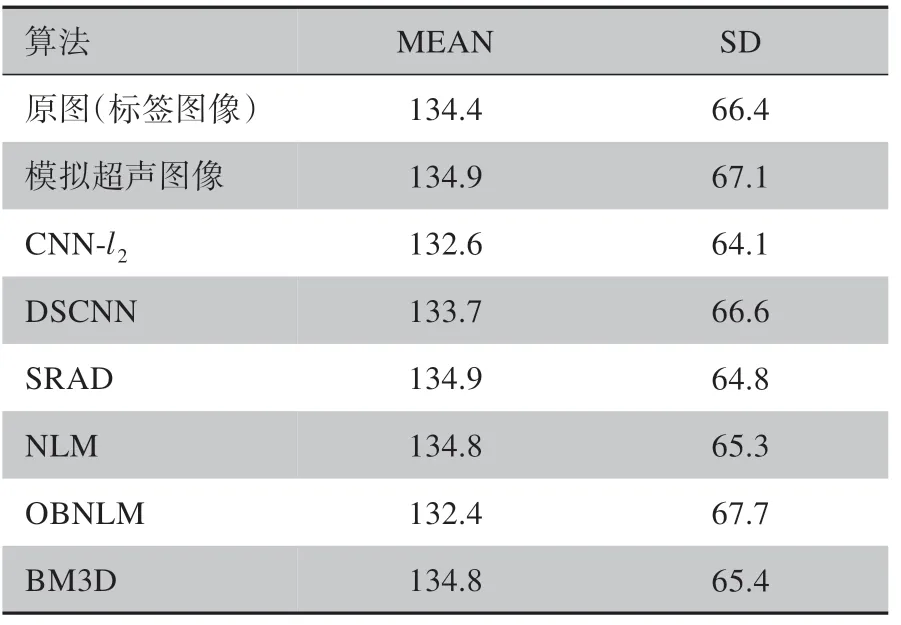
表4 不同算法在测试集样本数据（图2）上的统计特性Table 4 Statistical properties of different algorithms for sample data in test set(Figure 2 )

图2 不同去噪算法的去噪结果Figure 2 Denoising results of different denoising algorithms

综合以上关于去噪结果的视觉效果及4 项评价指标，可以看出DSCNN 能够有效地去除散斑噪声，极大地提升超声图像质量。

4 结语

散斑噪声作为超声图像纹理信息的组成基元，对散斑噪声的去噪处理面临着两难的困境，如何在提高超声图像质量的同时尽可能地保留纹理信息是本文研究的重点。本文提出的基于卷积神经网络的超声图像散斑去噪模型DSCNN，利用卷积神经网络学习复杂图像信息的能力，并针对去噪算法普遍存在的纹理信息损失问题提出一种低复杂度、低时间成本的解决方案。除此之外，本文还在实验中使用模拟超声成像技术合成超声图像，取代以往将散斑噪声简化为乘性噪声的粗略建模，并为神经网络提供充足而多样的训练数据，提高去噪模型的健壮性和泛化能力。DSCNN 在超声图像去噪方面主要具有以下优势：（1）在有效抑制散斑噪声的同时，较好地保留图像纹理信息；（2）去噪效果不依赖于人工调参经验；（3）去噪处理耗时短，不影响超声诊断的实时性，临床上具有实际应用价值。为使去噪算法更好地服务于临床诊断，未来将研究使用不成对的图像无监督地训练去噪模型，从根本上解决临床中无法获得与超声图像空间配准的可作为标签的无噪声图像难题，同时，这将意味着可以在训练集中添加真实的超声图像，使去噪模型的结果更加准确可靠。