主河道岸坡角和支流汇入量对泥沙冲淤的影响
2022-01-24付梁其李勋章何晓静胡腾腾刘飞诗
付梁其,李勋章,何晓静,胡腾腾,潘 磊,刘飞诗
(1.常州市金坛区水利规划服务中心,江苏常州 213200;2.常州市金坛区水资源管理服务中心,江苏常州 213200;3.江苏省水文水资源勘测局常州分局,江苏常州 213100;4.常州市金坛区水利建设管理所,江苏常州 213200;5.江苏远瀚建筑设计有限公司,江苏常州 213000)
0 引 言
水流对河道的冲刷会产生泥沙淤积,从而造成水工建筑物运行受阻,成为了城市河道修筑、疏浚过程中必须解决的技术问题。在支流与主河道汇合的汇流处,循环涡流的形成和流速的增加会导致汇流后的河道冲刷和泥沙沉积[1]。汇流处的流型很复杂,受许多因素的影响,如:支流与主流的比率(以下简称流量比)、主流与支流河道之间的动量传递速率等[2,3]。水流汇合处可分为六个水动力区域:①合流上游拐角处的停滞区;②合流点处的流动偏转区;③合流下游拐角附近的分离区;④主河道中出现最大流速区(分离区导致的水流收缩);⑤汇合后河道最大流速区下游的水流恢复区;⑥两个合流水流之间形成的剪切层。据前人研究[4,5],汇流处的河床剪应力增强是由于汇合点处主流和支流的组合,以及强涡产生的螺旋运动和动能。在文献[4,5]中,关于汇流区的水流流态和泥沙输移的研究已有不少报道,研究结果表明,将汇流角从15°增加到90°可使得底流速增加1.3 倍,较大的汇流角会显著增加最大冲刷深度。另外,当采用较大的汇流角和流量比时,泥沙淤积的高度增加。
河流生态保护和泥沙淤积治理已上升为重大的国家战略[6],揭示河流泥沙淤积的机制是各地生态经济区发展的基础。对于泥沙淤积研究,李泽刚[7]分析了黄河入海泥沙扩散、淤积的形成与演变等规律,提出了河口段河道整治和拦门沙治理等稳定黄河河口流路的对策。王恺忱[8]分析了黄河下游及河口河段冲淤特性,进行了黄河河口延伸改道对下游河道的影响研究,用实测资料证实了河口尾闾入海流路的绝对长度是河口河段和下游河道冲淤幅度与发展趋势的制约因素。胡春宏等[9,10]分析了水沙运动与演变基本规律,提出了黄河口治理的方向与措施。余欣等[11]通过试验研究了尾闾河道出汊机制,提出了出汊阈值、触发条件以及河口流路稳定综合判别指标。王崇浩等[12-14]利用一、二维连接数学模型研究了河口潮流与泥沙输移过程,对河口演变对下游河道反馈的影响进行了分析。上述泥沙淤积的研究成果有效地指导了各类河道的疏浚和整治[15,16]。由此,本文以常州市金坛区城市河道“畅流活水”工程为背景,研究在支流河道汇入主流河道过程中,主河道岸坡角、支流流量比和弗劳德数对汇流区冲刷的影响。
1 研究方法
1.1 理论分析
Ghobadian和Shafai-Bajestan 对考虑不同汇流角(60°、75°和90°)的冲刷模式进行了试验研究[17],并提出了汇流后最大冲刷深度(dse)和泥沙淤积高度(Hse)的近似计算方法,如下所示:
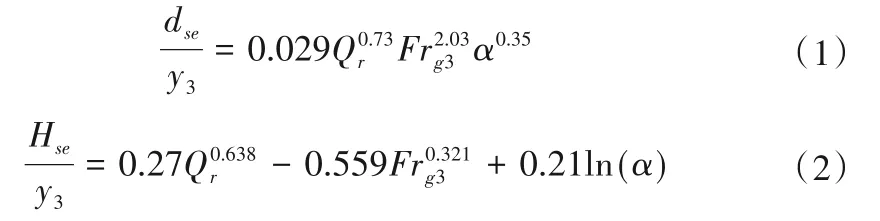
式中:dse为最大冲刷深度;Qr为支流与主流的流量比;y3为汇流后河道的水深;Hse为汇流后的泥沙淤积高度;α 为汇流角;Frg3为汇流后河道的密度弗劳德数。
Frg3的表达式如下:
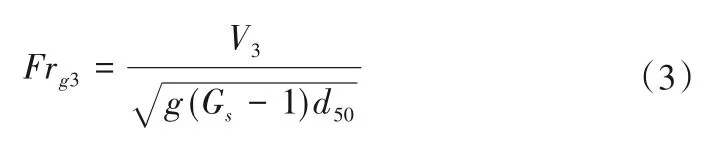
式中:V3为汇合后河道的流速;Gs为泥沙颗粒的比重(本研究中取2.63);d50为泥沙粒径中值。
基于以上理论,本文开展了量纲分析,并尽可能地全面考虑可能对汇流处冲刷有影响的不同变量。量纲关系式如下所示:
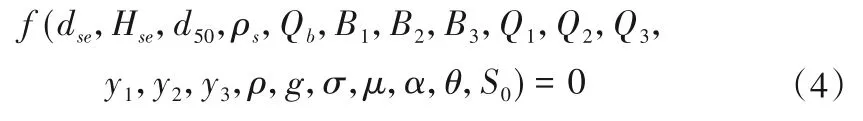
式中:ρs为泥沙颗粒密度;Qb为推移质;B 为渠道的底宽;Q 为渠道的流量;ρ为水体密度;g为重力加速度;σ为表面张力;μ为动力黏度;θ 为主渠道岸坡角;S0为汇流处主渠道纵向河床坡度。下标1、2和3分别指上游、支流和汇合后河道。
利用BuckinghamΠ 定理对汇流处冲刷的量纲分析结果如下式所示:
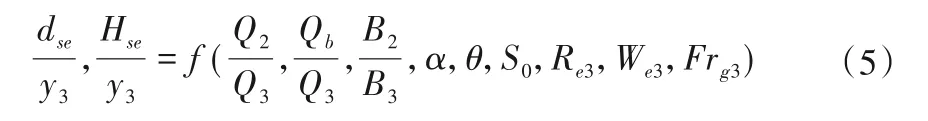
式中:Re为雷诺数;We为韦伯数。
由于实验中黏度和表面张力的影响可以忽略不计,因此本研究中没有考虑雷诺数和韦伯数。此外,汇流处上游不允许推移质运移,因此Qb可以删除。根据Gurram[18]研究结果,在亚临界流条件下,河床坡度对汇流处的流型影响可以忽略不计。由于所有实验都是在亚临界条件下进行的,因此本研究不考虑S0。实验采用恒定的汇合角α,即90 度汇合,则式(5)可简化为式(6):
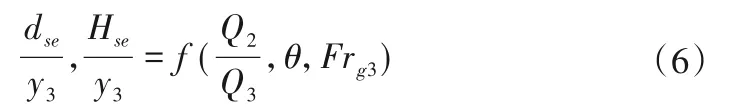
1.2 实验设置
在理论基础上,本文开展了水槽试验研究,共进行了64 次试验。图1 中,主水槽长6 m,宽50 cm,高50 cm;支流水槽长5 m,宽24 cm,高50 cm;支流水槽与主水槽垂直连接,即汇合角为90度。两个水槽的纵向河床坡度设为零,木片制成的底板安装在水槽底部上方14 cm 处,底板之间的空隙由沙子填充,然后在水槽中加载沙床。为了研究岸坡对汇流处冲刷的影响,本研究在主水槽中采用了45°、60°、75°和90°的不同倾角斜墙。图2展示了实验室中泥沙的冲刷与淤积。主水槽和支水槽都安装了供水机泵与闸阀,每台机泵的供水流量都经过试验,能够灵活控制流量,故而主流和支流的流量可以准确分配。
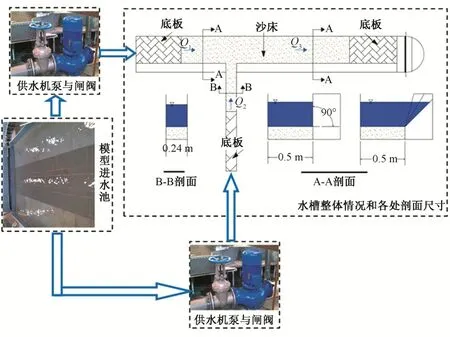
图1 实验装置示意图Fig.1 Schematic diagram of experimental device

图2 泥沙的冲刷与淤积(以45°岸坡为例)Fig.2 Erosion and deposition of sediment(45°bank slope)
实验采用的总排水量均为25 L∕s,具体流量由位于主水槽下游端的校准矩形堰来测量。本研究中汇合处连接的3个通道的流量值见表1。为了调节流量,首先在主渠道调节流量,同时关闭支流渠道出口闸门。然后,位于连接点的支流河道闸门逐渐打开,以建立支流流量。在主水槽下游端使用大量叠梁来调整尾水深度,调整范围为0.152~0.235 m,从而将密度弗劳德数调整在1.28~2.58 的理想范围内。此外,还使用了一个精度为±0.1 mm的超声波测量仪来测量水面高程。
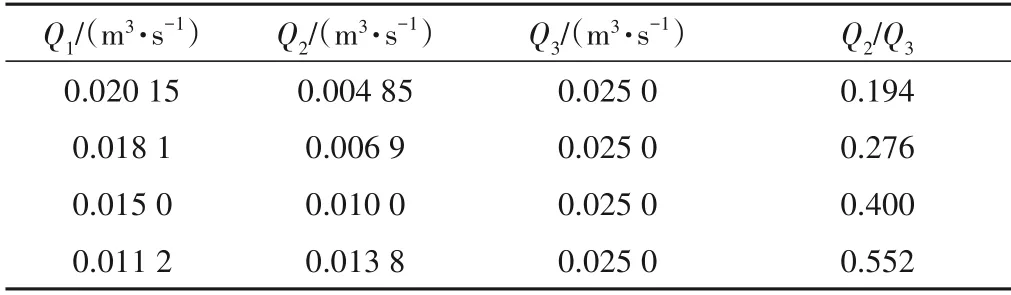
表1 汇流连接处的三个通道流量值Tab.1 Three channel flow values at confluence connection
在实验中,均匀沙被用作沉积物材料,d50=1.28 mm,标准偏差为1.32 mm。根据式(6)所提出的3 个无量纲参数,本研究在实验中采用了4 个岸坡角和4 个流量比,以评估流量比、汇合后水流条件和河岸坡度对汇合处冲刷的影响。此外,在实验室条件下,通过控制水流深度,对每一流量比采用四个弗劳德数和密度弗劳德数。每次试验结束时,在冲刷坑内建立平衡条件。在初步试验中,θ=45°时获得了最长的平衡时间。因此,在θ=45°的条件下,在72 h 内进行了一系列实验,以确保达到平衡条件。对于最大和最小流量比,在不到6 h 的时间内获得了几乎90%的最大冲刷深度。然后,在不干扰泥沙床的情况下小心地将水槽中的水排干;随后,使用分级杆测量冲刷坑的尺寸和泥沙淤积的高度。在图2中,在45°岸坡角的实验室水槽中显示了泥沙冲刷和淤积的形成。最后,利用SPSS统计软件进行多元回归分析,得到最大冲刷深度与泥沙淤积高度在上述参数下的无量纲经验关系。
2 结果与讨论
在每个实验中,汇流处观察到一对漩涡并向相反方向移动,从而引发河床物质的冲刷。同时,由于汇合处的水流收缩产生的高速导致了河床物质的输送,并在合流后河道中形成泥沙淤积。最后,随着水流断面的恢复(即增大),流速降低。
2.1 最大冲刷深度
图3为无量纲最大冲刷深度(dse∕y3)随密度弗劳德数的变化情况。如图3所示,虽然在所有流量比下,dse∕y3随Frg3增加而增大,但在最大流量比下,dse∕y3的增加率最高,见图3(d)。这一结果与Ghobadian 和Shafai-bajestan[17]提出的矩形横截面主河道的实验结果一致。对比图3(a)~(d)可以看出,对于给定的密度弗劳德数(Frg3)和岸坡角(θ),流量比的增加导致冲刷坑更深,即产生更大的dse∕y3。该结果说明了流量比的增加在汇流处分离区扩张中的作用,更大的流量比可导致更高的流速和河床剪应力,从而导致更深的冲刷坑。另一方面,最小的岸坡角(θ=45°)对应的dse∕y3最小,这可归因于岸坡角越小时,支流进入主河道的水流越缓,使得水流与河床物质的接触较小,冲刷最小。最后,岸坡角对冲刷深度的影响随Qr的增大而显著减小。换言之,当在汇流处建立适当的流量比时,河流的岸坡角才会影响冲刷深度。因此,本文认为河岸坡度对汇流处冲刷深度的影响在实践中不能忽略。通过多元回归方法(R2=0.83)得出公式(7)以近似计算无量纲最大冲刷深度,公式(7)如下:
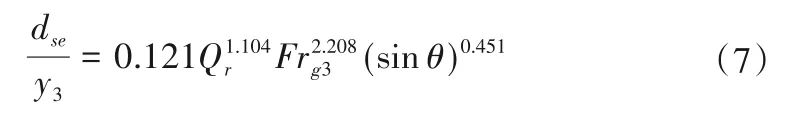
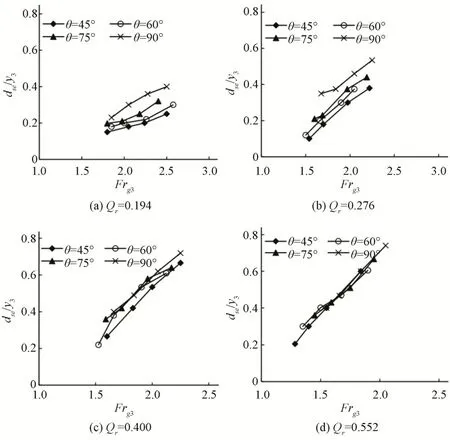
图3 无量纲最大冲刷深度随密度弗劳德数的变化Fig.3 Variation of dimensionless maximum scour depth with density Froude number
虽然岸坡角(θ)对冲刷深度有影响,但通过比较式(7)右侧3个变量的指数,可以得出θ对最大冲刷深度的影响小于密度弗劳德数(Frg3)和流量比(Qr)的影响。此外,图3 表明,对于较低的密度弗劳德数,冲刷深度被略微低估,而随着密度弗劳德数和岸坡角的增大,误差增大。
本研究认为,Ghobadian 和Shafai-Bajesta 的经验公式忽略了不同岸坡的影响,仅考虑了恒定岸坡(θ=90°)下不同汇流角的作用。而本研究的无量纲最大冲刷深度的散点图能够比较和验证前人研究的成果和假设,同时,本研究所提计算公式具有考虑河岸坡度的优点。
2.2 泥沙淤积最大高度
在每个实验的过程中,水槽内形成了一个泥沙淤积坝并逐渐向下游移动。当支流槽与主流槽的流量比增大时,水流变得平缓,而流量比和密度弗劳德数的减小则导致了较尖锐的淤积高度。图4 考虑了不同的流量比和岸坡角,并根据密度弗劳德数绘制了汇流处淤积的最大无量纲高度(Hse∕y3)变化情况。如图所示,当流量比增大到Qr=0.552时,θ=75°的实验结果与θ=90°的实验结果接近。此外,随着θ 的增加,当Qr=0.194、0.276、0.400 和0.552 时,Hse∕y3的平均增长率分别为41.7%、29.4%、27.8%和23.4%。通过多元回归方法(R2=0.80)得出公式(8)以近似计算无量纲最大淤积高度,公式(8)如下:
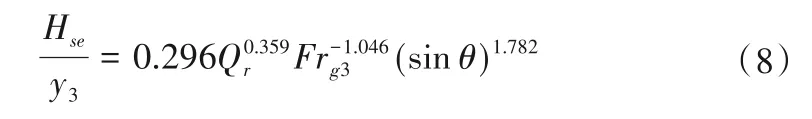
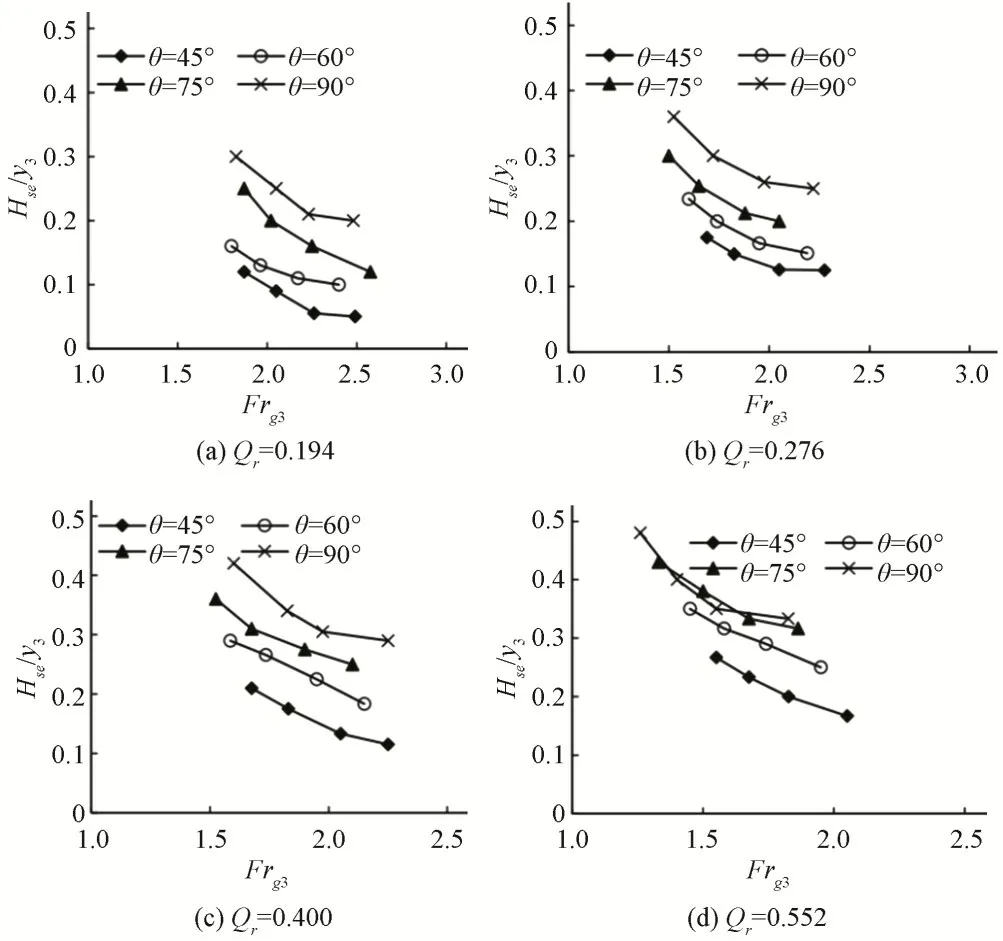
图4 不同岸坡角和流量比下最大无量纲淤积高度与密度弗劳德数的关系Fig.4 Relationship between maximum dimensionless deposition height and density Froude number under different bank slope angle and discharge ratio
根据式(8)右侧的指数可以得出,岸坡角对淤积最大无量纲高度的主要影响是隐含的,这一点与岸坡角对无量纲最大冲刷深度的影响不同。值得注意的是,较大的流量比(Qr)和岸坡角(θ)会导致较高的泥沙淤积高度,而较大的密度弗劳德数(Frg3)会降低河道泥沙淤积的最大高度。图4表明,密度弗劳德数越高,误差越小。此外,岸坡角的增加导致了淤积高度估计误差的增大。应用相同的假设,公式(8)得出的结果与Ghobadian和Shafai-Bajestan的结果非常接近。随着Frg3的增加,泥沙淤积的最大高度一般出现在下游方向离合流口较远的地方。根据不同的Qr和θ 值,本文可得对应4 个Frg3值的4 个最大淤积高度的位置。结果显示,在岸坡倾斜角度较小(θ=45°和60°)的情况下,在倾斜的河岸上近处产生了泥沙淤积。同时,当使用小流量比(Qr=0.194 和0.276)时,以及θ=45°和60°时,离汇流处较远的位置形成了泥沙淤积。相反,在θ=75°和90°的情况下,当实验室水槽中使用较小的流量比时,泥沙淤积出现在了汇合点,但流量比的逐渐增大会使泥沙淤积位置再次向下游移动。Shakibainia 等[19]指出,靠近汇合通道内壁的泥沙淤积的形成是由于流动分离区的压力降低所致。在当前的研究中,观察结果表明,当θ减小时,在距离汇合后河道起点较远的地方会产生泥沙淤积。另外,对于较缓的岸坡角,汇流下游似乎有一个较小的分离区,这是导致在距汇流后河道起点较远的位置形成泥沙淤积的原因。为检验本研究的有效性,本文使用Ghobadian 和Shafai-bajestan 的实验数据来验证本文的公式(7)和公式(8),对比结果见图5 和图6。如图所示,两者拟合效果较好,误差较小。
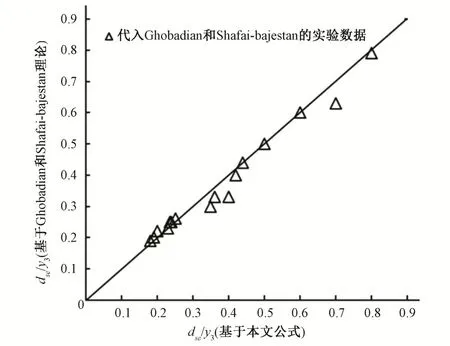
图5 Ghobadian&Shafai-bajestan 实验数据验证公式(7)Fig.5 Validation of formula(7)by Ghobadian&Shafai-bajestan
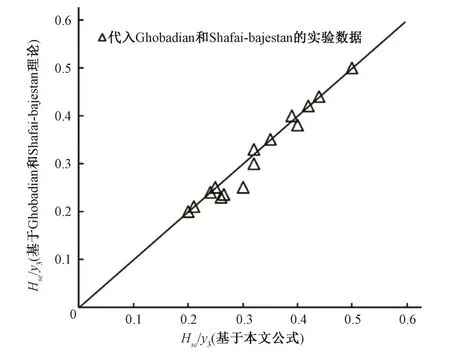
图6 Ghobadian&Shafai-bajestan 实验数据验证公式(8)Fig.6 Validation of formula(8)by Ghobadian&Shafai-bajestan
3 结 论
本文研究了主河道岸坡角θ、流量比Qr和密度弗劳德数Frg33个变量对汇流处冲刷和泥沙淤积的影响,得出以下结论:①在汇流处确定小流量比时,岸坡角对冲刷深度的影响最大;②对于给定的汇流处支流量,汇流后Frg3的增加使得最大冲刷深度增加,并降低了淤积高度;③岸坡角对淤积高度的影响大于对冲刷深度的影响;④本研究中,θ=45°和Qr=0.194 的试验效果最好,使最大冲刷深度减少了46%。 □
