一类新冠肺炎的流行病学模型稳定性研究

金德泉,陈芃合,王凯明

(1.广西大学数学与信息科学学院,广西 南宁 530004;2.广西大学广西应用数学中心,广西 南宁 530004;3.长安大学理学院数学与信息科学系,陕西 西安 710061)

1 引言

目前,新冠肺炎疫情在全球范围内大规模流行,对各国的社会经济生活造成了严重的影响[1-2].2020年3月,世界卫生组织(WHO)正式宣布新冠肺炎为大流行病.因此,根据新冠肺炎传播的流行病学特点,建立符合新冠肺炎传播规律的数学模型,刻画新冠肺炎的内在传播机制,并进一步定性定量的研究其传播规律,将对制定和评估防控措施方面具有重要的指导作用.

研究传染病传播模型的主要方法包括SIS模型、SIR模型、SEIR模型与SEIS模型等.文献[3]利用离散时间的SIS模型,模拟了新冠肺炎变异的传播过程.文献[4]利用经典的SIR模型与支持向量机方法,对印度尼西亚新冠肺炎的传播进行了预测.文献[5]通过对SEIR模型进行改进,即使用SEIQRDP模型对南非新冠肺炎的发展趋势进行了拟合.文献[6]基于广义SEIR模型,预测了新冠肺炎在中国的传播趋势.文献[7]研究了具有饱和接触率的SEIS模型的动力学性质,得到了决定疾病绝灭或持续生存的基本再生数.文献[8]讨论了一类具有常数输入且传染率为非线性的SEIS流行病传播数学模型,给出了疾病消失和成为地方病的基本再生数.

以上研究成果在很多方面成功刻画了新冠肺炎的一些传播特点,为新冠肺炎的防控给出了理论依据.但是SIS模型与SIR模型没有充分考虑潜伏期对于新冠肺炎传播的影响,难以很好地刻画此次新冠病毒存在潜伏期长的特性.同时,与传统的天花、流感、麻疹这一类流行病不同,目前已发现的新冠肺炎患者被治愈后依旧存在再次感染的可能性,而接种疫苗也只能降低新冠肺炎的因病死亡率和重症率,获得抗体后依旧可能感染新冠肺炎.另外,新冠肺炎具有很强的变异性,这也显著削弱了抗体在预防新冠病毒感染中的作用.但是一般意义下的SEIS模型与SEIR模型难以准确地描述新冠肺炎的这些特点.综上所述,针对新冠病毒因病死亡率率高、传染力强、潜伏期长、抗体在预防感染中作用不显著等特点[9],需要建立一类能够反映这些特点的流行病学模型来恰当地描述此次新冠肺炎的动力学特征.

通过建立一类描述新冠肺炎传播动力学机制的改进SEIS模型,证明了新冠肺炎传播的无病平衡点和地方病平衡点全局渐近稳定性的条件,并通过数值仿真的方法进行了分析验证.

2 预备知识

2.1 常微分方程稳定性理论

定义2.1[10]设平面自治系统

且O(0,0)是系统(1)的平衡点,则线性系统

引理2.1[11]设O(0,0)是几乎线性系统(1)的初等奇点,则当O(0,0)是其线性近似系统(2)的鞍点、结点或焦点时,它也必是系统(1)的鞍点、结点或焦点,且具有相同的稳定性.

引理2.2[12]设高维线性系统

的系数矩阵 A 的特征根为 λ1,λ2,···,λr,则有

(i)若 λ1,λ2,···,λr均具有负实部,则系统 (3)的零解是渐近稳定的;

(ii)若λ1,λ2,···,λr中至少有一个具有正实部,则系统 (3)的零解是不稳定的.

若 λ1,λ2,···,λr中没有正实部的根但是有零根或零实部的纯虚根,则当零根或零实部的纯虚根的初级因子都是一次的,系统(3)的零解是稳定的.当零根或零实部的纯虚根中至少有一个的初级因子次数大于一次时,系统(3)的零解是不稳定的.

2.2 奇异摄动法

引理2.3[13]对摄动系统

若系统(4)满足

(i)它的退化系统

其中g(x,y,ε)=0是一条曲线,即存在函数y=φ(x),使得g(x,φ(x),0)≡0;

(ii)f(x,y,ε)和 g(x,y,ε)关于 x,y,ε都有连续光滑导数;

(v)矩阵gy(x*,y*,0)的特征值的实部都是负的,则如果完全系统(4)具有局部稳定的平衡点,那么当ε充分小的时候该平衡点是全局稳定的.

2.3 传染病模型

SIS传染病模型将人口分为两类:易感者类,记为类S,该人群目前无病,且无免疫能力,可以被传染而患病;患者类,记为类I,该人群已经患病,且可以把疾病传染给类S人群.用S(t)和I(t)分别表示t时刻上述两类人群占总人口的比例.SIS模型的假设条件为:

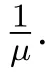
(b)人群中两类成员均匀分布,传播方式为接触传播.单位时间内一个患者类I的成员和其他类S成员接触率为常数λ,与类S成员的接触总数为λS,则单位时间内与类S成员接触总数为λNSI,即单位时间内类I成员增加的数量,称为发病率.

SIS传染病模型假设患者病愈后并未产生免疫能力,仍为S类成员.因此,SIS模型[15]为

由S(t)和I(t)的定义及人口数为常数可知S+I=1,则模型(6)可化简为

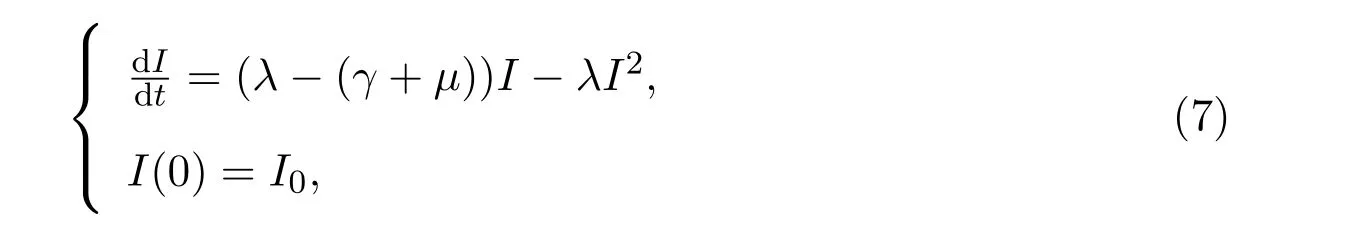
将方程(7)改写为

当传染病具有潜伏期时,可以将处于潜伏期人群比例设为E;同时,如果治愈或接种疫苗后的人群具有长期免疫力,可将其比例设为R.由此可以得到SIS模型的改进形式,如SEIS和SEIR等流行病模型.

3 SEIS模型及其平衡点的全局稳定性

新冠肺炎具有不同于传统传染病的一些特点.首先,在接种新冠疫苗之前,新冠肺炎发病导致的死亡率很高;其次,新冠肺炎有一个很长的潜伏期,且在潜伏期中具有传染性;第三,个体在感染新冠和接种了新冠疫苗仍然有可能感染新冠肺炎.对于具有潜伏期,且不具备长期免疫性特点的传染病,常用的模型是SEIS模型.在传统的SEIS模型中,E代表处于潜伏期的人群比例.但是,新冠肺炎具有与传统传染病不同的流行病学特点.首先,由于大流行背景下检测条件的限制,潜伏期感染者自愈及转化为患者的比例难以精确统计.其次,新冠肺炎的潜伏期感染者具有一定的传染性,但难以确定其接触感染率.最后,新冠肺炎的潜伏期和发病期的界定仍存在争议,界限不够清晰,这些都对建立较为准确的新冠肺炎传播的动力学模型带来了较大的困难.

为了解决这些问题,该模型对处于新冠肺炎潜伏期的感染者人群进行更为细致的划分.首先,由于新冠肺炎病毒变异性强,同时潜伏期感染者自愈后所带抗体作用时间短,将感染后未发病、未检出,不具传染性的自愈人群归入类S.其次,将感染了新冠肺炎,通过咽拭子检测未检出,但最终发展为新冠肺炎患者的人群归入类E.最后,将处于潜伏期,但可以通过咽拭子检出的感染者人群归入类I.由此得到如下关于新冠肺炎传播的改进SEIS模型:

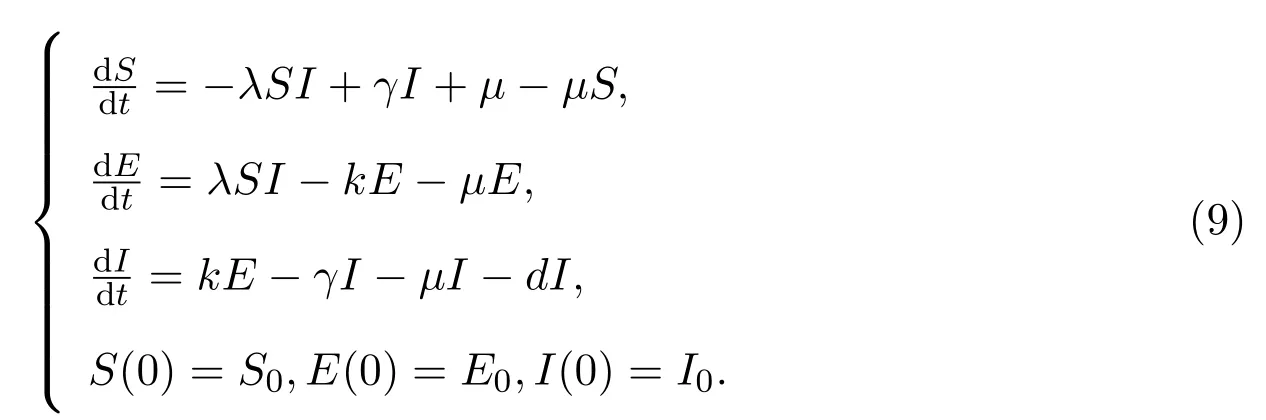
在该模型中,λ的定义修改为单位时间内一个类I的成员和类S成员接触感染率,即接触并造成感染的比例.k是单位时间内E类人群中的个体由潜伏期的感染者发展为新冠肺炎患者的比例,即发病率.d是单位时间内类I的人群因为新冠肺炎引起死亡的比例,即因病死亡率.其他都如2.3节中定义.则由计算可得,基本再生数为

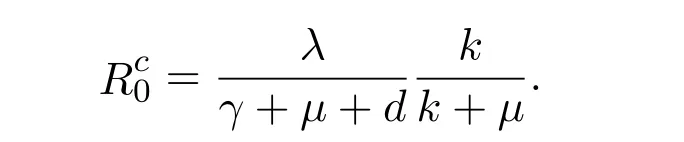
Rc0的流行病学意义是,在病期内每个新冠肺炎患者平均感染其他健康者的人数.为了方便分析模型的动力学性质,将模型(9)化简为

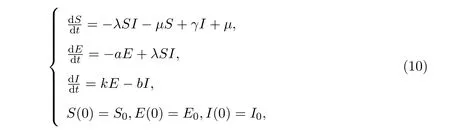
其中a=k+µ,b=γ+µ+d.

在以下的讨论中,将结合奇异摄动理论[14],研究系统(10)平衡点的全局稳定性.奇异摄动理论允许一些非摄动系统通过尺度变化为摄动系统.下面利用Lyapunov函数和Dulac函数,以及奇异摄动方法和理论证明系统平衡点的全局稳定性.

设D={(S,E,I)|S＞0,E＞0,I＞0,S+E+I≤ 1}.

命题 3.1D为系统(10)的正向不变集,且全局吸引.

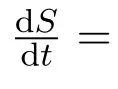
3.1 系统变量的尺度变换

首先对时间进行尺度变换,令τ=kt.再分别对S,E和I尺度变换,令

则模型(10)变为

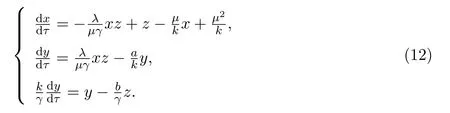
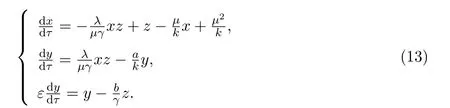
令ε=0,则得到退化系统

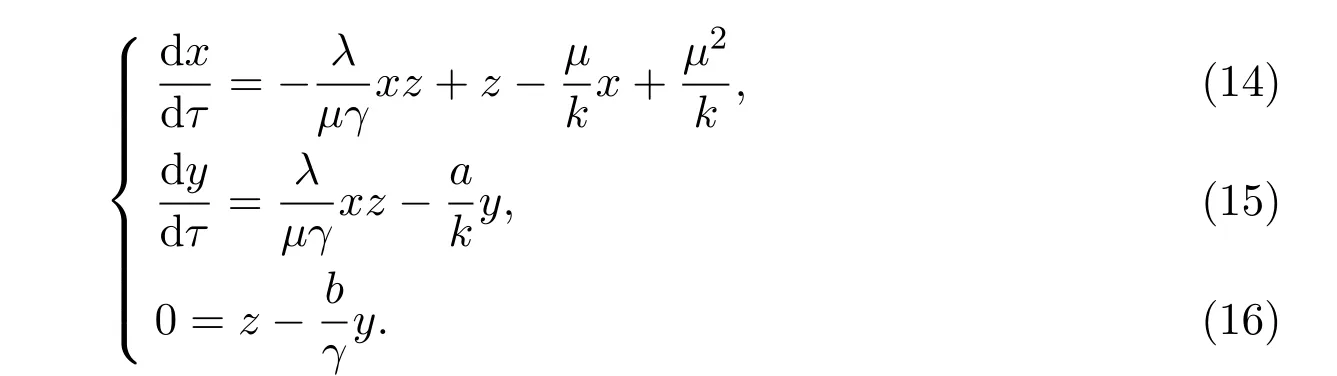
下面将对退化系统(14)-(16)进行讨论.

3.2 退化系统的平衡点性质

通过计算可以得到系统(17)具有两个平衡点(µ,0),

根据流行病学性质,前者称为无病平衡点,后者称为地方病平衡点.为了证明系统(17)平衡点的全局性质,本文先证明系统(17)平衡点的局部性质.

证明(1)令 x=X+µ,y=Y,则系统(17)变为

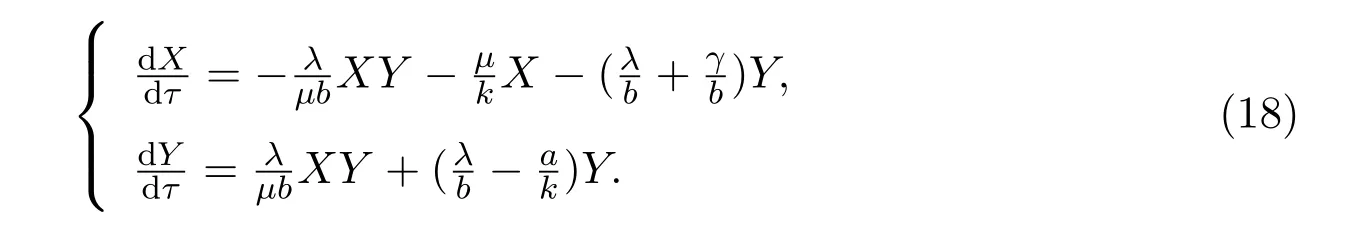
它的线性近似系统为

系统(19)的系数矩阵为

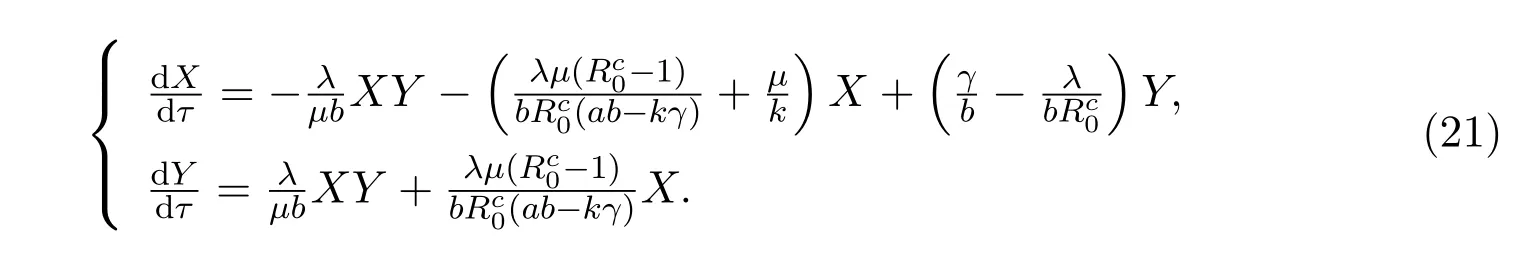
因此,它的线性近似系统为

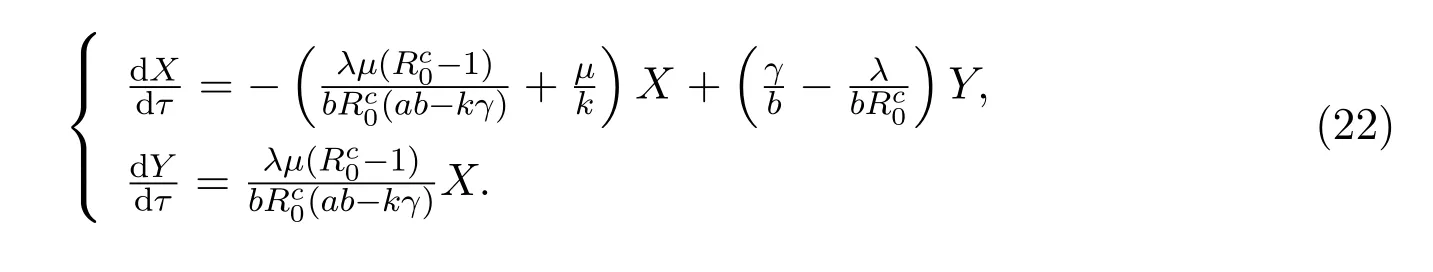
它的系数矩阵为

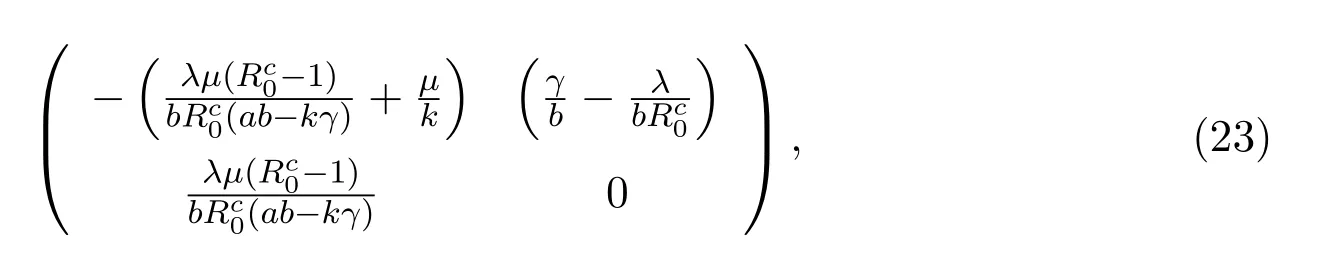
特征方程为m2+pm+q=0,其中

当Rc0＞1,p和q都是正的.因此系统(17)的无病平衡点是局部渐近稳定的.

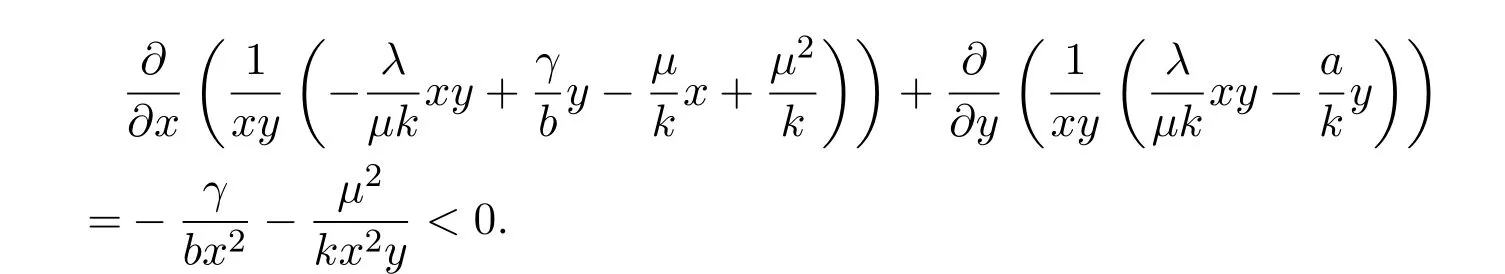
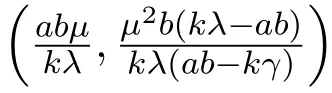
3.3 无病平衡点的全局稳定性

命题3.4当Rc0＜1时,系统(10)的无病平衡点是全局渐近稳定的.

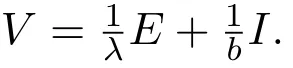
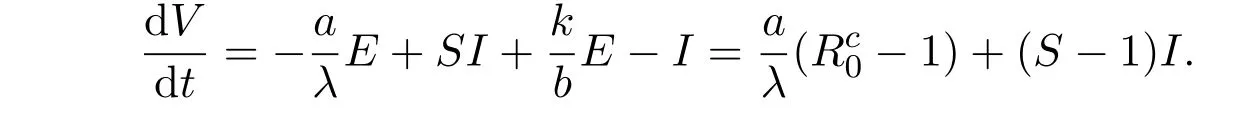
3.4 系统 (10)地方病平衡点的全局稳定性

下面证明系统(13)满足定理2.3.

命题3.5如果Rc0＞1且ε充分小,系统(13)的地方病平衡点是全局渐近稳定的.

证明对该模型,有

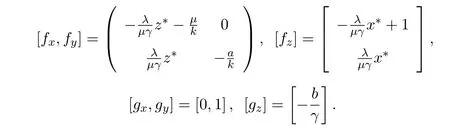
可得

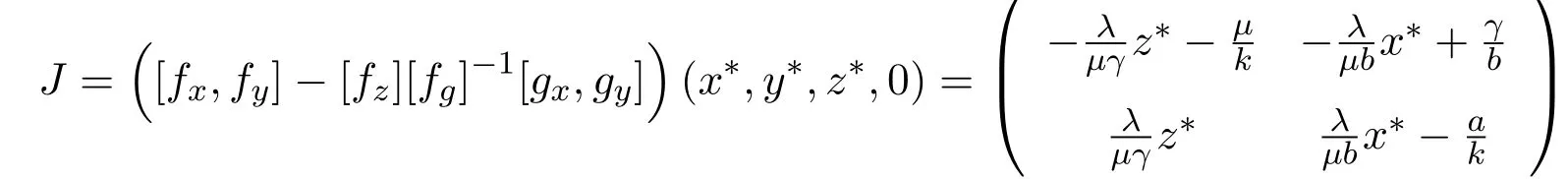
它的特征方程为m2+pm+q=0.其中当Rc0-1＞0时,

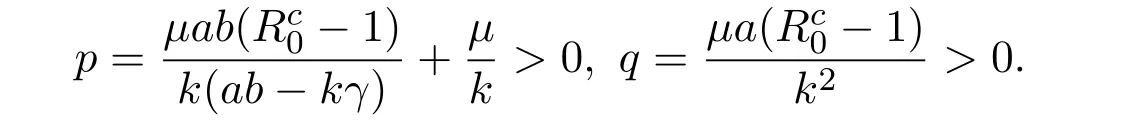
所以J当Rc0-1只有负的特征值时,满足条件(iii).

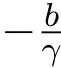
由命题3.1,可知只要t足够大,S+E+I≤1,即命题3.3成立,完全系统的地方病平衡点是局部渐近稳定的.所以由定理2.3可知,如果Rc0＞1且ε充分小,系统(13)的地方病平衡点是全局渐近稳定的.

4 参数估计与数值模拟

4.1 参数估计

4.1 数值模拟

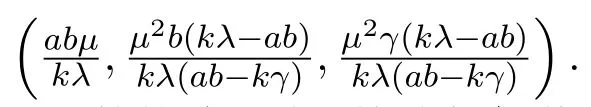
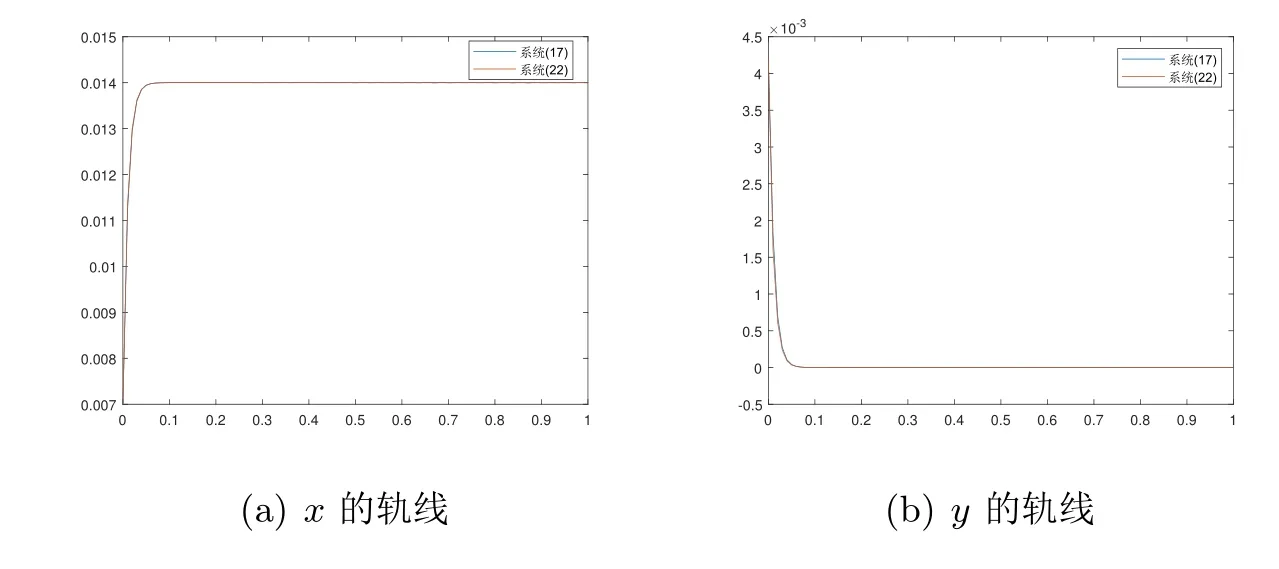
图1 f=0.01时x和y的轨线,此时ε=0.0007,Rc0=0.05

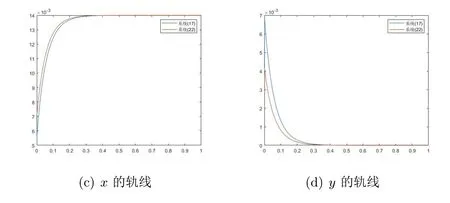
图2 f=0.05时x和y的轨线,此时ε=0.00037,Rc0=0.24

图3 f=0.2时x和y的轨线,此时ε=0.00175,Rc0=0.95

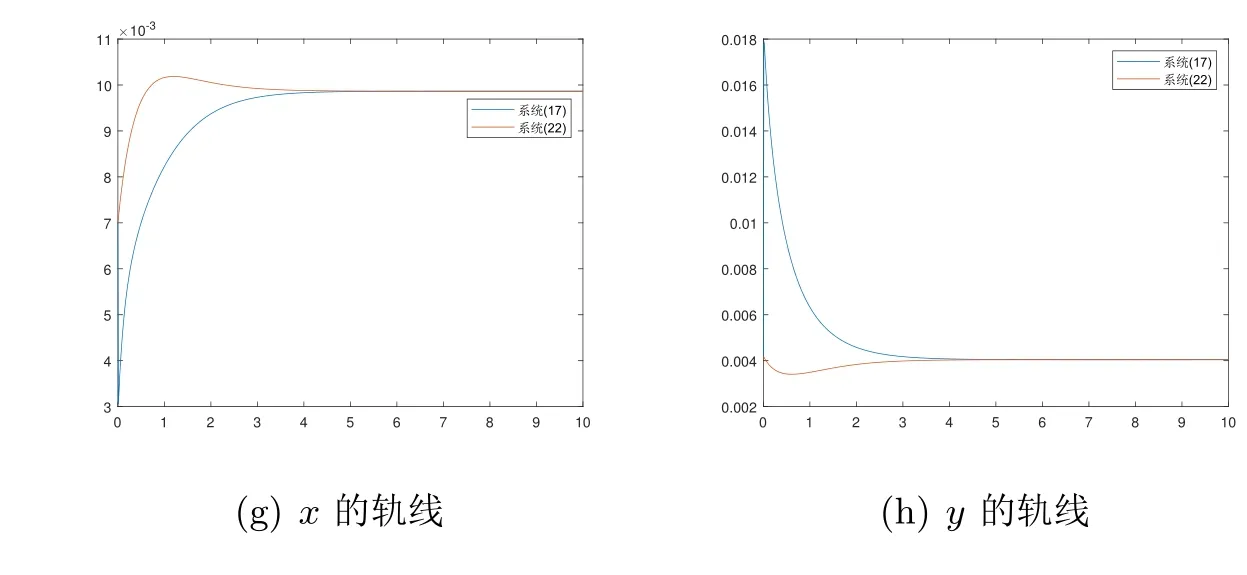
图4 f=0.3时x和y的轨线,此时ε=0.003,Rc0=1.4

由上面的数值实验可以看到,当Rc0＜1时,系统(13)和系统(17)的轨线都收敛于无病平衡点(0.014,0),当ε很小时符合得相当的好.但随着ε的增大,两个系统的轨线的差距开始增大.当取到f=0.3时,轨线不再收敛于无病平衡点,而是收敛于地方病平衡点(0.01,0.0039).

为了观察地方病平衡点的性质,取 λ=30,这在实际情况中已经是很大的值.当 f=0.1时,则

此时地方病平衡点为(0.0099,0.0041).

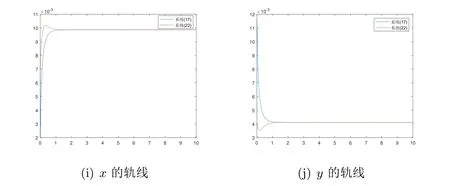
图5 f=0.1时x和y的轨线,此时ε=0.000778,Rc0=1.42

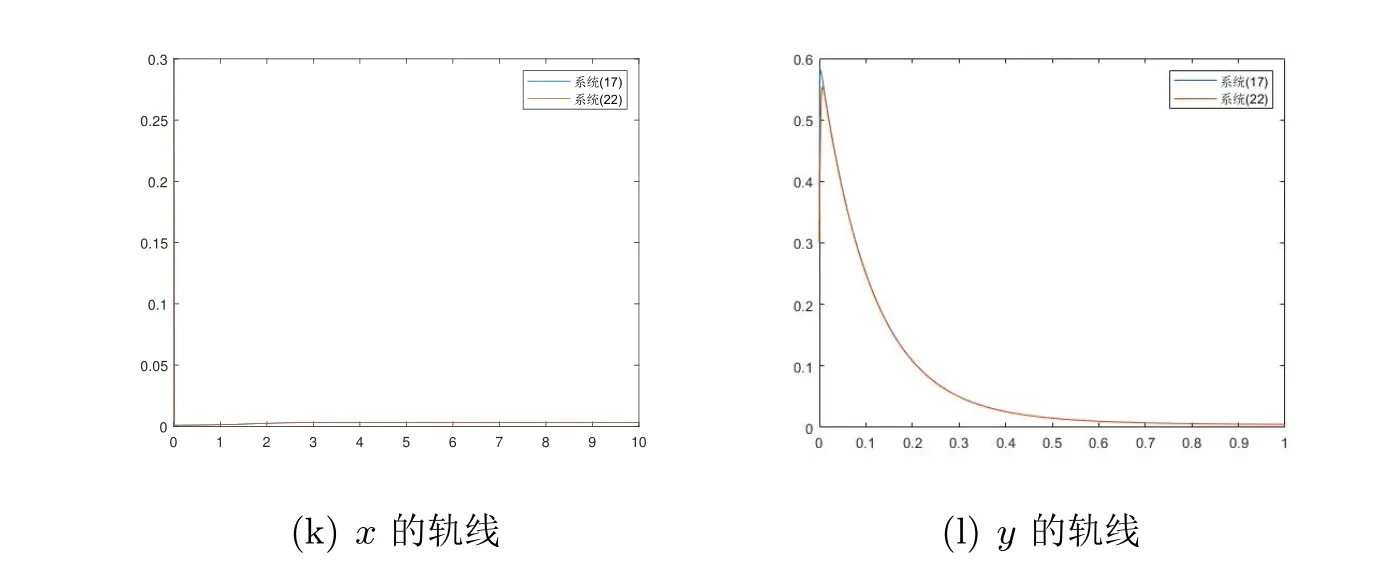
图6 f=0.3时x和y的轨线,此时ε=0.003,Rc0=4.26

通过上面的实验可以看到,在上述几种情况下,Rc0＜1时模型的无病平衡点和Rc0＞1时模型的地方病平衡点的稳定性是明显的,退化系统和完全系统在平衡点附近的性质是一致的,在一定条件下可以运用退化系统来模拟完全系统的性质.这与该SEIS模型的理论证明是一致的.

5 结论

疾病的传染率、潜伏期、因病死亡率是传染病流行的重要因素,影响着流行病的动力学性质,因此对具有类似新冠肺炎传播特点的动力学传染病模型进行定性分析具有现实意义.由以上的证明结果和仿真实验可知,要防止新冠肺炎的流行,必须减少基本再生数Rc0.若Rc0＜1,即一个患者在平均患病期能传染的最大人数小于1时,患者和潜伏期内感染者的人数会逐渐减少,疾病自然逐渐消亡;反之,若Rc0＞1,即一个患者在平均患病期能传染的最大人数大于1时,患者人数会逐渐增加,但不会无限增加,在一定时间后,易感染人群比例、潜伏期感染者比例、患者比例会趋于一个平衡状态,疾病将始终存在而形成地方病.

为了减小基本再生数,可以采取的方法包括:

(1)减少λ,即患者接触其他健康者的数量.对患者进行隔离可以达到此效果;

(2)提高治愈率γ,即缩短治疗时间.这可以通过提高医疗条件达到此效果;

(3)减少k,即减少感染者的发病率;这可以通过研究相应的疫苗达到此效果.

(4)当因病死亡率d增大时,基本再生数Rc0也会减少.这表明,新冠病毒虽然存在出现毒性加强的变异而导致因病死亡率过高的情况,但由于死亡率过高降低了Rc0,该变异类型很可能只能在局部地区造成疫情加重的情况,难以在大范围地区形成大规模流行.

由前面的讨论可以看到,在没有特效药的情况下,即使人群普遍接种了疫苗,如果放任人群在无防护情况下发生大规模聚集和流动,依然存在基本再生数过高,无法根除新冠肺炎流行,从而使其发展为在一定范围内长期流行的传染病的风险.因此,在国外新冠肺炎仍处于大流行的背景下,在研制出防护能力较强的高效疫苗和特效药之前,仍然需要采用包括佩戴口罩、控制跨国人口流动等措施来降低接触感染率,维持国内来之不易的较好的防疫形势,保证国内社会生产和人民生活的正常运行.

值得注意的是,该SEIS模型是在简化了一些情况和条件下得到的,这使得模型的预测能力受到了一些影响.为此,在进一步的工作中,可以对人群进行更细致的分类,进一步完善模型,以此提高模型的预测能力和预测精确性.