Metrics of the Fell topology that preserve the metric of the underlying space
2022-01-23YangZhongqiangWeiGuo
Yang Zhongqiang,Wei Guo
(1.School of Mathematics and Statistics,Minnan Normal University,Zhangzhou 363000,China;2.Department of Mathematics and Computer Science,College of Arts and Science,University of North Carolina at Pembroke,Pembroke North Carolina 28372,USA)
Abstract:For any locally compact separable(complete)metric space(X,d),let Cld(X)denote the space of all non-empty closed subsets of X equipped with the Fell topology.It is proved that there exists a compatible(complete)metric D on Cld(X)that preserves the metric d of X.For the n-dimensional Euclidean space Rn,such a metric D is explicitly constructed,but the constructed D on Cld(Rn)is not complete.Hence,seeking a complete metric on Cld(Rn)is an interesting problem.On the other hand,for the space Conv(Rn)of all non-empty closed convex subsets of Rnequipped with the Fell topology,an explicit complete compatible metric DConvthat preserves the usual metric of Rnhas been constructed in this paper.
Keywords:metrics of Fell topology,isometric extension,absolute expansion,retraction,Alexandroffcompactification
1 Introduction
1.1 The Fell topology
Given a topological space X,let Cld*(X)denote the family of all closed sets of X equipped with the Fell topology(also known as H-topology[1],hit-or-miss topology[2],or Choquet-Matheron topology[3]),which has the following subbase(see Reference[2]):

where U is any open subset of X and W is any open subset of X with compact complement.The subspace Cld(X)=Cld*(X){Ø}is often considered when the empty set Ø of X is not of interest.
The Fell topology on arbitrary underlying spaces(Hausdorffor not)was introduced by Fell in 1962 for constructing the regularized dual space of C*-algebra[1,4].Reference[5]re-discovered this topology when investigating the distribution and Choquet Theorem of random sets.References[1,4,5]included the empty set,thus considered the space Cld*(X)of all closed subsets of X which is then always compact.Earlier investigation of this topology were in fact given by Reference[6]and Reference[7]which studied the topologies of closed convergence in locally compact separable metric spaces and locally compact Hausdorffspaces,respectively.
As a variation of the Vietoris topology,defined as the meet of the co-compact topology and lower Vietoris topology[2,8],the Fell topology is closely related to the Vietoris topology,Hausdorffmetric,Wijsman topology,and upper Kuratowski topology(a topologization)(see References[2,5],and the summary in Reference[9]).
1.2 The problem
Let(X,d)be any locally compact separable metric space.It is well-known that,when(X,d)is a compact metric space,the Fell topology on Cld(X)is induced by the Hausdorffmetric dHdefined as follows:

where Bd(C,ε)={x ∈ X:d(x,c) < ε for some c ∈ C}is the ε-neighborhood of the closed subset C in X.
In particular,dHpreserves the metric d of X,i.e.,dH({x},{y})=d(x,y)for any x,y∈X.As(X,d)and the subspace Cld1(X)={{x}:x∈X}of(Cld(X),dH)that contains all singleton sets of X are isometrically homeomorphic,dHis regarded as a isometric extension of d.
On the other hand,locally compact separable metric spaces(X,d)appear as the natural domain for many applications,e.g.,manifolds in dynamics or underlying spaces of random sets.In this case,the Fell topology on Cld(X)is metrizable(see References[2,6,10]),but it is not induced by the Hausdorffmetric dHif(X,d)is not compact.
Hence,a natural question arises:For any locally compact separable metric space(X,d),whether or not there exists a metric D on Cld(X)that is compatible with the Fell topology and,simultaneously,preserves the metric d of X.Further,when such a metric D exists,an explicit construction of D becomes theoretically important and practically useful,e.g.,for characterizing the stochastic convergence of random closed sets in probability theory,investigating(random)fuzzy sets,and exploring the collective behavior of a cluster of particles in dynamics(Section 1.4)
The purpose of this paper is to present a constructive proof of the existence of D(Section 2)and,based on this proof,provide an explicit construction of D for X=Rn(Section 3).
1.3 Literature survey
By Bing′s “extending a metric” that any metric on a closed subset of a metrizable space can be extended to a metric on the whole space(a result known to Haudorff)[11],the metric d of X can be extended to a metric of Cld(X).However,the proof of this existence theorem is based on a covering theorem and does not provide a feasible approach for actually achieving such a metric.
So far,four compatible metrics of the Fell topology are known.One(the stereographic distance ρ)is on Cld*(X),constructed by using the Alexandroff compactification of X(see References[6,12-15]),another is on Cld(X),constructed bypassing the Alexandroff compactification of X(see Reference[16]),still another is the Hausdorff-Buseman metric which is compatible with the Fell topology on Cld(X)but not on Cld*(X)[15,17],and the fourth is on Cld*(X),also constructed bypassing the Alexandroffcompactification of X(Reference[9]).However,none of the above metrics preserves the metric d of X.
Moreover,it is known that a metric d of X can be extended to a metric of the Fell topology on Cld*(X)if and only if d is of compact-type,i.e.,the metric d of X can be obtained by restricting a metric of ωX on X(Reference[18]).In particular,when X=Rn,the stereographic metric is of compact-type;but the usual metric of Rnis not(thus an isometric extension on Cld*(X)does not exist(Ø∈ Cld*(X))).
In summary,a metric D of Cld(X)that preserves the metric d of X remains unknown,even for X=Rn.
1.4 Physical background
The hyperspace Cld(X)provides a framework for exploring the properties of a given space X due to the relation that the subspace Cld1(X)of Cld(X)that contains all singleton sets is homeomorphic to X.Further,a metric D of Cld(X)that preserves the metric d of X is useful and convenient in handling metric-dependent properties of various mathematical structures defined on(X,d),e.g.,stochastic convergence of a random closed set(RACS),convergence of the hypographs of u.s.c.fuzzy sets,and collective properties of dynamical systems(e.g.sensitivity,expansivity and transitivity).
Random hitting on larger suspended particles by smaller particles(as atoms or molecules)in a liquid or gas can result in irregular,stochastic motion of these larger particles,causing them to jiggle in the whole space.One such example is the Brownian motion,for which the physical reason and statistical mechanics were first provided by Einstein a hundred years ago.While the motion of each individual particle is of concern,it is more important to understand the evolution of a whole cluster of particles and the relation between these individual motions.Here,the stochastic behavior of a cluster of particles can be well suited through a RACS.
The hypograph of a u.s.c.function or fuzzy set is a closed subset of the corresponding product space.This standard method of identifying u.s.c.(l.s.c.)functions with sets in a product space via their hypographs(epigraphs)is an enormously in fluential approach in stochastic geometry and optimization,and has been extensively studied in the literature,e.g.,References[2,12,19-24].Recently,hypograph approach has been further advanced in various aspects,e.g.,References[17,25-36].
Viewing RACS as bona fide random elements,we need to have the space of closed subsets of X as a separable and complete metric space for stochastic analysis,such as defining the concept of convergence in probability for RACS(see Reference[15]).Salinetti and Wets noticed this problem earlier and realized the difficulty of handling the stereographic distance ρ:For X=Rn,“one possibility would be to use the Hausdorffmetric between closed sets constructed by using the stereographic distance on X.However,it is not clear how to translate and use these constructions in an operational setting” (see Reference[37]).Here,the difficulty comes from the fact that,when ρ is restricted to Cld1(X),the resulting space(Cld1(X),ρ)is not isometric to the original space(X,d)although they are homeomorphic,even for X=Rn.
In dynamics,the study of individual orbits separately is generally not enough in describing the orbit structure and other dynamical properties of a given system(X,d,f).Rather,a complete characterization requires a consideration of the simultaneous iteration of a cluster of points and,in particular,an investigation of the evolution relation between the orbits of these points.For instance,to describe a transitive system,we need to characterize the iteration of an open set U of X,resulting in the iteration sequence f(U),f2(U),···,fk(U),···.To generalize the concept of topological entropy to non-compact metric spaces,such as those introduced by References[38-41],(k,ε)-spanning sets and(k,ε)-separated sets are utilized where the orbits of all points in a compact set are considered at the same time(connected to Kolmogorov′s size of a metric space: ε-entropy and ε-capacity;see Reference[42]).In the case of sensitiveness(resp.,expansiveness),the orbit of a point is compared with that of some nearby points(resp.,with that of all nearby points).In Astrophysics,while the evolution of each individual orbit of a single celestial object is of concern,it is more important to know the evolution of a whole galaxy and the relation between the orbits of those objects in the galaxy.
In these applications,the main difficulty is that a topological structure over the subsets of X is unavailable in X itself.In contrast,a topological structure over sets is available in Cld(X).It should be also noted that,in the original space X,there is no an operation between two points;in contrast,in the hyperspace Cld(X),operations between two points F and H such as intersection F∩H and union F∪H,are admitted.
Consequently,a metric D of Cld(X)that preserves the metric d of X is useful for promoting above applications,in particular for exploring metric-dependent properties of relevant systems defined on X.
It should be pointed out that,at present,because of the lack of such a metric D,one can only employ those non-isometric hyperspace metrics specified previously in Sections 1.2 and 1.3 in the applications[19,28,43-45].
In the remainder of the paper,Section 2 investigates the existence of a compatible metric on Cld(X).In Section 3,a compatible metric on Cld(Rn)by utilizing a retraction from Cld(Rn)to Rn.Section 4 studies complete metrics on Cld(X).Finally,the conclusion is given in Section 5.
2 The existence of the desired metric D
Lemma 2.1Let(X,d)be a non-compact locally compact separable metric space and ωX=X ∪ {ω}the Alexandroff compactification of X.Then there exists a compatible metric d*on ωX such that

ProofChoose a compatible metric d1on ωX.We may think d(x,ω)=+∞ for any x∈ X which is nothing but d(x,ω)+r≥ s for any real numbers r,s.
Now we define a metric d*on the set ωX as follows:

It is straightforward to verify that d*is a metric on the set ωX and d*satisfies

Therefore,the topology induced by d*is weaker than that induced by d1.As the topology induced by d1is compact,the topologies induced by d*and d1are the same.Hence,d*is our required metric.
Corollary 2.1If X=Rnwith the usual Euclidean metric dn,then d*in above Lemma 2.1 can be chosen as the stereographic metric calculated by the usual metric dn+1of Rn+1.
ProofLet q:Rn→Snbe the stereographic projection,where Sn⊆Rn+1is the unit sphere centered at(0,···,0,1),i.e.,
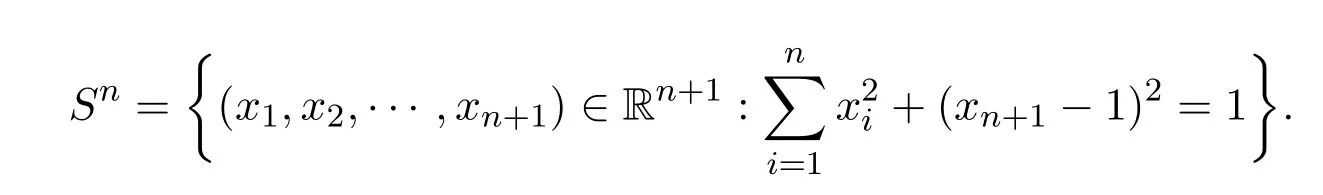
It is clear that dn+1(q(x),q(y))< dn(x,y)for xy.
A separable metric space X is called an absolute expansion(AE)if for any separable metric space Y and closed subspace A of Y,every continuous map from A to X can be extended to a continuous map from Y to X.A separable metric space X is an AE if and only if it is an absolute retract(AR),that is,for every separable metric space Y which contains X as a closed subspace,there exists a continuous map(called a retraction)r:Y→X such that r(x)=x for every x∈X.It is known that Rnis an AE.More general,any convex set of a locally convex real linear space is an AE.But Snis not an AE.For more information on AE theory,we refer to References[46,47].The question that whether or not every real linear space is an AE(that is,the removal of the condition local convexity in the above result),was a well-known and long standing open problem before Cauty gave a negative answer in 1994(see Reference[48]).
The following Lemma and its proof are well-known(see Reference[47]).For the sake of completion,we provide a proof here.
Lemma 2.2For every separable metric space(X,d)there exists an AE(Y,d**)and an isometric embedding from(X,d)into(Y,d**).
ProofLet CB(X)be the set of all bounded continuous functions from X to the space R of real numbers equipped with the sup-norm,that is,for every f∈CB(X)

Fix a point x0∈X and define a map φ:X→CB(X)as follows:

Note that for every x,z ∈ X,|φ(x)(z)|≤ d(x,x0)and hence φ(x)∈ CB(X).Moreover,for any x,y∈X,

Therefore φ is an isometric embedding from X into CB(X).Let Y be the convex hull of φ(X)in CB(X),that is,Then Y is convex and hence an AE.With the norm metric on Y,φ:X→Y is an isometric embedding.

Remark 2.1If(X,d)is itself an AE such as Rn,then we may simply choose(Y,d**)=(X,d)in Lemma 2.2.But even in this case,(Y,d**)obtained in the proof of Lemma 2.2 is not necessarily identical with(X,d).
The existence of the metric D in the following result is implied by Bing′s Theorem[5](see Section 1.3).However,in the proof below,a specific construction of D is provided.
Theorem 2.1For any locally compact separable metric space(X,d),there exists a compatible metric D on Cld(X)such that D induces the Fell topology and

for any x,y∈X.
ProofIf X is actually compact,the Hausdorffmetric induces the Fell topology and preserves the metric d of X.Thus,we assume that X is not compact.By Lemma 2.1,we may choose a compatible metric d*on ωX such that

for any x,y∈X(in particular,when X=Rn,d*can be chosen as the stereographic metric as so-selected in Corollary 2.1).Then(Cld*(ωX),d*H)is a compact metric space.Note that F → F ∪{ω}defines an embedding from Cld(X)into Cld(ωX).Thus
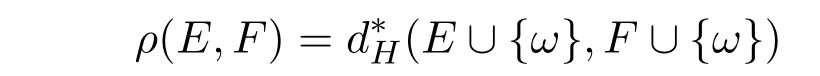
gives a compatible metric on Cld(X)(this ρ is the stereographic distance indicated in Section 1.3 when X=Rn).Moreover,for any x,y∈X,we have

By Lemma 2.2,we can consider(X,d)as an isometric subspace of an AE(Y,d**)(in particular,when X=Rn,(Y,d**)can be chosen as Rn,as so-selected in Corollary 2.1).Let i:X→Y be the corresponding isometric embedding.It is trivial to verify that the subspace Cld1(X)={{x}:x∈X}of Cld(X)that contains all the singleton sets is closed in Cld(X)and r:Cld1(X)→X defined by r({x})=x is continuous and onto(in fact,a homeomorphism).By identifying x with i(x),r:Cld1(X)→Y is a well defined continuous map.Thus,as Y is an AE and Cld(X)is a(locally compact)separable metric space,r:Cld1(X)→Y can be expanded to a continuous map r:Cld(X)→Y.Now we define

Obviously,D is a metric on the set Cld(X)and D(E,F)≥ ρ(E,F)for any E,F ∈Cld(X)(see Remark 2.2).Thus,for any sequence{Fm}in Cld(X)and

Conversely,if ρ(Fm,F) → 0,then d**(r(Fm),r(F)) → 0 since r:(Cld(X),ρ) → X is continuous,implying D(Fm,F)→0.This shows that the topologies induced by D and by ρ are identical,and hence D is a compatible metric on Cld(X).

Therefore,D is our required metric.
Remark 2.2For non-singleton closed sets E and F with EF,it is possible that r(E)=r(F).When this happens,we have ρ(E,F)=D(E,F) > 0 and d**(r(E),r(F))=0.On the other hand,when X=Rn,if(Y,d**)is chosen as Rn(Remark 2.1)and d*as the stereographic metric(Corollary 2.1),then for any two different singleton sets{x}and{y},we have

3 Constructing the desired metric D for Rn:a retraction from Cld(Rn)to Rn
Let X be Rnand O=(0,0,···,0)be the original point in Rn.In this section,we are interested in an explicit construction of D holding the properties described in Theorem 2.1,thus providing a concrete metric of the Fell topology on Cld(Rn)that preserves the usual metric d of Rn.
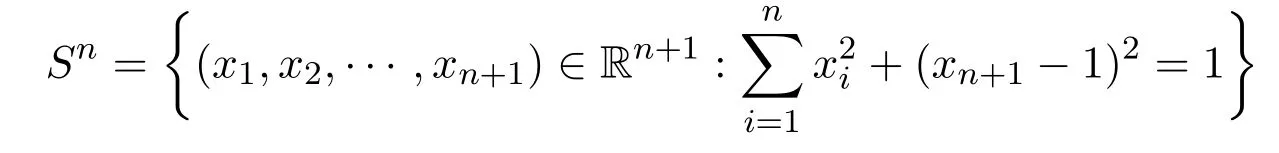
As mentioned in Remark 2.1,we can choose(Y,d*)=(X,d)since X=Rnis an AE.Choose the n-dimentional sphere as the Alexandroff compactification of Rn,and q:Rn→ Sn{(0,0,···,0,2)}as the stereographic projection.The metric of Snis the one that is obtained by restricting the usual metric of Rn+1on Sn,as so-selected in Corollary 2.1.
Recall that ‖x-y‖ ≥ ‖q(x)-q(y)‖ for any x,y ∈ Rn,where||·||is the usual norm.Therefore,to give our metric on Cld(Rn),it remains to construct the required retraction R:Cld(Rn)→Rn.
To define a natural retraction R:Cld(Rn)→Rn,first every singleton set is mapped to that point.Then for any closed subset F of Rnwith more than one point,we construct R according to n=1 and n>1 separately.
For n=1,to define a retraction r:Cld(R)→R,we will use the continuous map f:P=(-∞,0)×(0,+∞)→R defined by

Properties of f are summarized in the next lemma(verifications are elementary):
Lemma 3.1The function f defined above satisfies:
(i)x<f(x,y)<y for any(x,y)∈P;
(ii)f is continuous;
(iii)For every a > 0 and ε> 0,there exist δ∈ (0,a)and α > 0 such that|f(x,y)-a|< ε for any(x,y)∈ P with x < -α and|y-a|< δ;
(iv)For every ε> 0,there exists δ∈ (0,ε)such that|f(x,y)| < ε if either x ∈ (-∞,-ε]and y∈ (0,δ)or x∈ (-δ,0)and y∈ [ε,+∞).
Now we define r:Cld(R)→R as follows.For every F∈Cld(R)(with one or more than one point),let
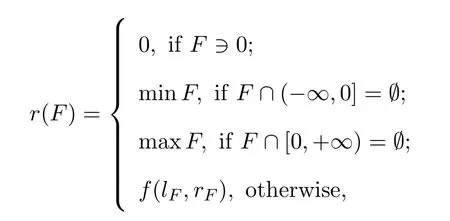
where

Then we have
Lemma 3.2The map r:Cld(R)→R defined above is continuous,r({x})=x for every x∈R.
ProofTrivially,r({x})=x for every x∈R.We verify that r is continuous at every F ∈ Cld(R).That is,for every ε> 0,there exists a neighborhood U of F in Cld(R)such that

We consider all the possibilities:F /∋0 or F ∋0,where the former is divided into three further cases(Cases A,B and C below).
Case A:F /∋ 0 and F ∩ (-∞,0]ØF ∩ [0,+∞).By Lemma 3.1(ii),there exists δ> 0 such that|f(x,y)-f(lF,rF)|< ε if(x,y)∈ P with|x-lF|< δ and|y-rF|< δ.Moreover,we may assume lF+δ< 0 < rF-δ.Let Ul=(lF-δ,lF+ δ),Ur=(rF- δ,rF+ δ)and K=[lF+ δ,rF- δ].Then

is a neighborhood of F and satisfies(2).
Case B:F∩(-∞,0]=Ø.Then r(F)=minF>0.It follows from Lemma 3.1(iii)that there exist α > 0 and δ∈ (0,r(F))∩ (0,ε)such that|f(x,y)-r(F)|< ε for any(x,y)∈ P with x< -α and|y-r(F)|< δ.Let

Then U is a neighborhood of F and satisfies(2).
Case C:F∩[0,+∞)=Ø.Similar to Case B.
Case D:F ∋ 0.Then r(F)=0.Choose δ> 0 that satisfies the condition in Lemma 3.1(iv)for the given ε,and let U=(-δ,δ)-.Then U is a neighborhood of F and satisfies(2).In fact,for every E∈U,if r(E)is defined in one of the first three lines in the definition of r,then r(E)∈ (-δ,δ)⊂ (-ε,ε).If r(E)is defined in the forth line in the definition of r,then(-δ,δ)∩ {lE,rE}Ø.The(-ε,ε)∩ {lE,rE}contains either one or two points.In both cases,it follows from Lemma 3.1(i)and(iv),it always holds r(E)=f(lE,rE)∈ (-ε,ε).
Now we continue to construct the retraction R:Cld(Rn)→Rn.At first we define t:Cld(Rn)→R as follows:t(F)=inf{‖x‖:x∈F},F ∈Cld(Rn).
Lemma 3.3The map t:Cld(Rn)→R is continuous.
ProofFor every ε> 0 and F ∈ Cld(Rn),let t(F)= ‖x0‖,where x0∈ F.Let U=B(x0,ε)and K=(K= Ø if‖x0‖-ε< 0).Then U-∩(RnK)+is a neighborhood of F and t(U-∩(RnK)+)⊆ (t(F)-ε,t(F)+ε).Thus t is continuous.
Now,for every i=1,2,···,n,we define ψi:Cld(Rn)→ Cld(R)by

for F∈Cld(Rn).
Lemma 3.4
Each ψi:Cld(Rn) → Cld(R)in(3)is well-defined,is continuous and satisfies ψi({(x1,···,xi,···,xn)})={xi}for every(x1,···,xi,···,xn) ∈ Rn.
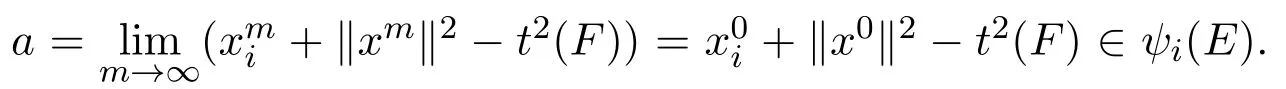
Secondly,we show that

is continuous.Suppose F ∈ Cld(Rn).For every open set U in R,if ψi(F)∈ U-,then there exists x=(x1,···,xi,···,xn)such that xi+‖x‖2-t2(F)∈ U.Thus there exists an open set V ∋ x in Rnand δ> 0 such that,for every y=(y1,···,yi,···,yn) ∈ V and s ∈ (t(F)-δ,t(F)+δ),we have yi+‖y‖2-s2∈ U.By Lemma 3.3,there exists a neighborhood U of F such that|t2(E)-t2(F)|< δ for every E ∈U.Let W=U∩V-.Then W is a neighborhood of F and,for every E∈W,we have that|t(E)-t(F)|<δ and there exists y=(y1,···,yi,···,yn)∈ E ∩V.Thus yi+‖y‖2-t2(E)∈ U ∩ψi(E).That is,ψi(E) ∈ U-.Moreover,for every compact set K in R with ψi(F)∩ K= Ø.Trivially,there exists r>0 such that For every x=by our assumption,


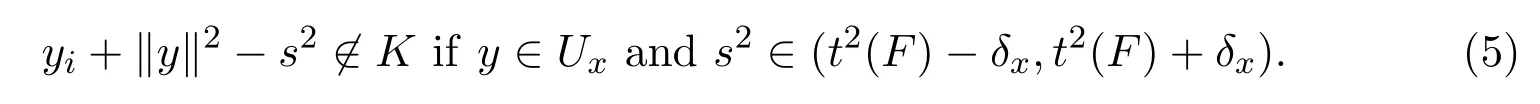

Lastly,it is clear that ψisatisfies ψi({(x1,···,xi,···,xn)})={xi}for every(x1,···,xi,···,xn) ∈ Rn.
Remark 3.1ψi:Cld(Rn)→ Cld(R)defined in(3)is a modification of the induced map Pi:Cld(Rn)→Cld(R)by the i-th projection pi:Rn→R.The reason for this modification is that,first,pi:Rn→R is not a closed map and therefore,Pi(F)needs not to be closed for a closed set F of Rn;and second,if we simply replace:Cld(Rn)→Cld(R)is not continuous.For example,when n=2,let Fk={(0,0),(1,k)}and F={(0,0)}.Then Fk→F in Cld(R2)but
Let us recall the natural retraction r:Cld(R)→R given at the beginning of this section.By putting this r and ψi′s in(3)together,we have established the following result:
Theorem 3.1The map R:Cld(Rn)→Rn,defined by

is continuous and satisfies R({x})=x for every x∈Rn.
Remark 3.2It is not hard to see that the map R:Cld(Rn)→Rndefined in Theorem 3.1 does not satisfy that R(F)∈ F for every F ∈ Cld(Rn)for n=1,2,···.In fact,there does not exist any continuous map R:Cld(Rn)→Rnsatisfying R(F)∈F for every F ∈ Cld(Rn).Otherwise,let Y={x∈Rn:‖x‖≥1}.Then R|Cld(Y)→ Y is a retraction from Cld(Y)to Y.Therefore,Y would be a retract of Cld(Y).But,it is known Reference[49]proved that Cld(Y)is homeomorphic[-1,1]ω{0}(this fact is also true for n=1 though Y is not connected in this case)and hence Cld(Y)is an AR,and it is well-known that Y is not an AR,which contradicts the fact that every retract of an AR is an AR.
Remark 3.3It seems that there exists no a “very natural” method to define a retraction from Cld(Rn)to Rn.But,for Conv(Rn)={C∈Cld(Rn):C is convex},we may define a map P:Conv(Rn)→Rnby P(C)being the unique point x∈C such that‖x‖=t(C).Then it is continuous(see Reference[50])and satisfies P(C)∈ C for every C∈Conv(Rn)and hence P({x})=x for every x∈Rn.Therefore P:Conv(Rn)→Rnis a natural retraction from Conv(Rm)to Rn.It is easy to verify that Conv(Rn)is closed in Cld(Rn).It was proved in Reference[50]that Conv(Rn)is homeomorphic to Rn×[0,1]∞for n>1 and Conv(R)≈R×[0,1].Hence they are ARs.Thus there exists a retraction S:Cld(Rn)→Conv(Rn).How do we construct such a map?The natural map mapping every closed set in Rnto its closed convex hull defines a map from Cld(Rn)to Conv(Rn)satisfying its restriction on Conv(Rn)and seems ideal.But,unfortunate,it is not continuous in our topology!
By Theorem 3.1,along with Theorem 2.1 in Section 2,the desired metric D that is compatible with the Fell topology on Cld(Rn)and preserves the metric of Rn(D({x},{y})=dn(x,y)for x,y∈Rn)is constructed as follows:
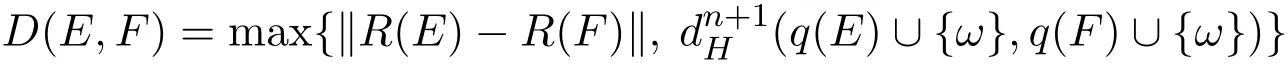
for E,F∈Cld(Rn),where(q(E)∪ {ω},q(F)∪{ω})is ρ(E,F)given in Section 2.Moreover,as indicated in Remark 3.3,if we restrict on Conv(Rn),then we can use the retraction P:Conv(Rn)→Rnto define a very natural metric

for E,F∈Conv(Rn).
Example 3.1We give some examples.
(a)If E,F∋O,then R(E)=R(F)=O and hence

(b)If E={O}and S(r)={x∈Rn:‖x‖=r}for r>0,then
R(E)=R(S(r))=O and D(E,S(r))=(q(E)∪{ω},q(S(r))∪{ω})=Note thatD(E,S(r))=0 andD(E,S(r))=2.
Moreover,

(c)If E={O}and,F is a non-empty convex unbounded closed set.Then it is not hard to verify that

Moreover,if xi> 0 for all x=(x1,···,xi,···,xn)∈ F and all i.Then ‖R(F)‖ =t(F).Thus

Therefore,D(E,F)→+∞ if t(F)→+∞.
(d)For the sake of simplicity and intuitive geometry,we consider some pairs of parallel lines in R2.

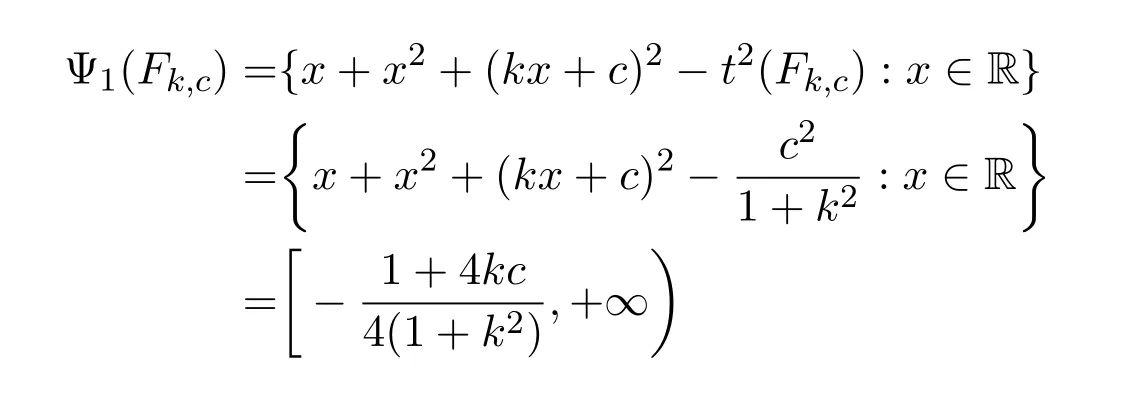
and
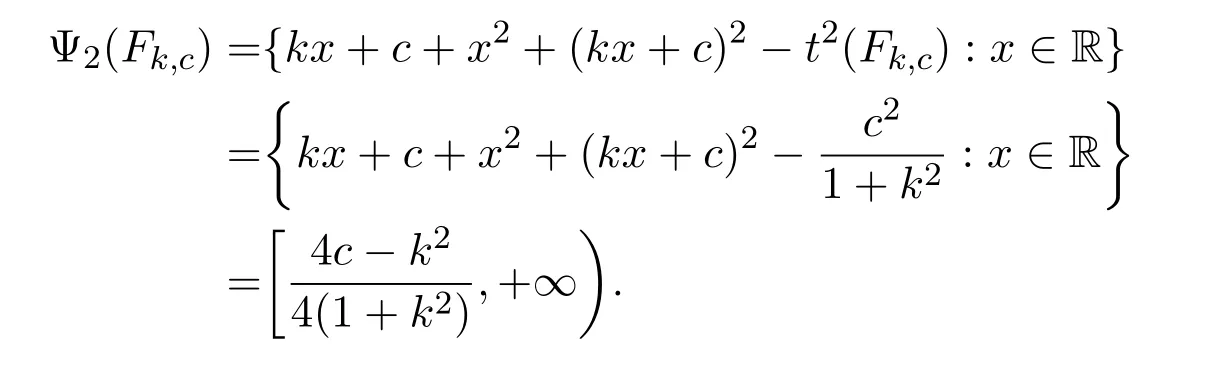
Let
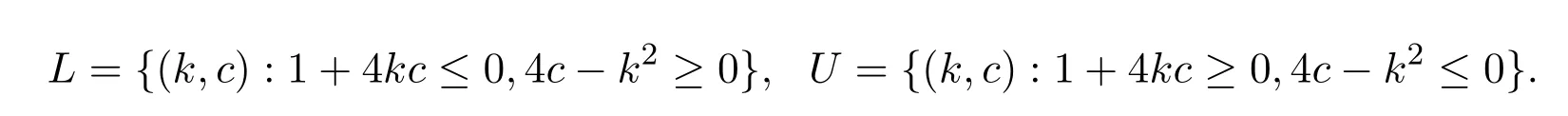
Then for every(k,c)∈L,

and for every(k,c)∈U,R(Fk,c)=O.Thus,for(k,c1),(k,c2)∈L,



Therefore,D(Fk,c1,Fk,c2)→ 0 if(c1,c2)→ (∞,∞)in this case.However,this statement does not hold for the former case.For otherwise pairs(k,c1),(k,c2),we can also calculate D(Fk,c1,Fk,c2).
Since Fk,c∈Conv(Rn),we can also calculate DConv(Fk,c1,Fk,c2).Then it is not hard to verify that

for any pair of(k,c1),(k,c2).That is,DConv(Fk,c1,Fk,c2)is the distance of the parallel straight lines Fk,c1and Fk,c2.
4 Complete metric on Cld(X)
Let us recall that a metrizable space X is topologically complete if there exists a complete admissible metric on X.It is well-know that a metrizable space X is topologically completed if and only if X is a Gδ-subspace of some complete metric space.We have the following general result:
Theorem 4.1For every topologically compete space X and its closed subspace A,if d is a complete admissible metric on A,then there exists a complete admissible metric D on X such that D|A×A=d.
ProofBy Bing′s Theorem[11],we can think that d is an admissible metric on the whole space X.Let(,)be the completion of(X,d).Then X is a Gδ-subspace and A is closed subspace ofsince|A×A=d is complete.Thus let XGk,where Gkis open infor every k.For every k,define a continuous map fk:→[0,1]as follows


It is not hard to verify that φ is a closed imbedding from X into×R∞,and φ(a)=(a,1,1,···)for every a ∈ A.Since R∞is topologically complete there exists a complete metric ρ on R∞.Then D1((x,s),(y,t))=max{(x,y),ρ(s,t)}is a complete metric on the space×R∞.Therefore we may define a complete metric D on X as follows D(x,y)=D1(φ(x),φ(y)).Then D is our required metric.
Corollary 4.1For every locally compact separable complete metric space(X,d),there exists a complete metric D on Cld(X)such that D({x},{y})=d(x,y)for any x,y∈X.
For D and DConvdefined in Section 3,we have the following theorem:
Theorem 4.2The metric DConvon Conv(Rn)is complete.For any n,D constructed in Section 3 is not complete on Cld(Rn).

Hence we can put a question:
Question 4.1How do we define a complete admissible metric on the space Cld(Rn)?
5 Concluding remarks
The metric of the Fell topology constructed in this paper preserves the metric of the underlying space.Consequently,the underlying space as well as other structures defined on the underlying space(such as dynamical systems)can be isometrically and conjugately embeded into the induced hyperspace(hyperspace system),which is a clear advantage that fulfills the requirement of the applications where the concern is metricdependent properties.In contrast,all other known metrics of the Fell topology do not preserve the metric of the underlying space.
Regarding the construction of the metric D,ρ separates all closed sets including singleton sets of X as it is a metric and satisfies ρ({x},{y}) ≤ d(x,y);the general retraction r in Theorem 2.1 may not separate some closed sets of X that contain more than one point(thus may not be a metric of the hyperspace)but does maintain the distance between points of X.As a combination of ρ and r(maximum of the two),D separates all closed sets and maintains the distance between points of X.Moreover,r is different from Bing′s extension of a metric as the range of the former is X but the range of the latter is[0,∞).In particular,for X=Rn,the constructed metric D,retraction R and metric ρ possess all above properties.
Finally,it should be pointed out that the metric DConvon Conv(Rn)is complete.But the metric D is not complete on Cld(Rn).
