Infinity,where some of the key concepts of analysis start to fall apart
2022-01-23JeffreyYiLinForrest
Jeffrey Yi-Lin Forrest
(Department of Accounting Economics Finance Pennsylvania State System of Higher Education at Slippery Rock,Slippery Rock,PA 16057,USA)
Abstract:This paper studies the concepts of actual and potential infinities by addressing whether or not they are different from each other.After constructing an example that shows how these concepts can and do lead to different answers,we look at the impacts of assuming either that they are the same or that they are different.Then,we turn our attention to checking how the current state of affairs of modern mathematics unconsciously applies both of these two assumptions simultaneously depending on which one is needed to produce desired conclusions.Based on the discussions of this paper,we pay a new visit to the Berkeley and Russell′s paradoxes and find that the shadow of the former paradox still presently lingers,while the latter is nothing but simply a self-contradictory proposition and a fallacy.
Keywords:actual infinity,Berkeley paradox,mathematical induction,potential infinity,Russell′s paradox,foundations of mathematics
1 Introduction
Since over two thousand years ago,the concept of infinity has been examined by various great minds throughout the recorded history.Under the name of infinity,the concept is divided into the ones named actual infinity and those known as potential infinity.The former means a present progressive tense or a forever,ongoing and neverending process,while the latter a present or past perfect tense or a process that actually ends or had ended.
Historically,Plato was one of the earlier scholars who talked about both actual infinities and potential infinities in his dialogues.And it seems that Aristotle was thefirst person who accepted the concept of potential infinities,while rejected the realistic likelihood of actual infinities.Because of Zeno′s paradox and many others alike,ancient scholars provided arguments against any intelligent usage of the concept of infinities.Consequently,the idea and explicit mentioning of the concept were circumvented at least on the surface in the area of mathematics.This historical fact explains why when calculus in the 16th hundred experienced difficulties,mathematicians replaced the needed actual infinities by potential infinities through developing the ε- δ and ε-N language and the theory of limits.And along such efforts,Leibniz′s approach of monads was abandoned.Even so,the acceptance of actual infinities by Leibniz and others eventually led to the wide-range receipt of such infinities as a genuine subject of study.That helped pave the way for Cantor to naturally introduce and develop his na¨ıve set theory.Although this theory initially suffered from great difficulties for the majority of the mathematical community to recognize its legitimacy,it eventually won successes and assisted with the confirmation of actual infinities as a viable subject matter of mathematics.It then helped revive Leibniz′s theory of monads in the 1960s.
However,the successes of Cantor′s set theory were short-lived.It soon had to face with the challenges of various paradoxes and inconsistencies,as calculus experienced several hundred years earlier.Similar to what mathematicians did with the foundation of calculus,scholars rebuilt their desired set theory on the ground of axioms by referencing how Euclidean geometry was developed.By means of axioms,the existence of actual infinities is presumably given,leaving behind the question of whether the concept of actual infinities is the same as that of potential infinities unaddressed.This open question is exactly what this paper is about.In particular,we demonstrate that these two types of infinities do lead to contradictory outcomes,and that modern mathematics widely employs either one of these two types of infinities or both depending on what is desired to accomplish.In other words,modern mathematics faces the challenge of the following paradoxical scenario:to the question of whether or not actual and potential infinites are the same,modern mathematics provides both positive and negative answers.
Based on what is revealed in this paper,we revisit the Berkeley and Russell′s paradoxes and find that the shadow of the former still lingers around,while the latter stands for a self-contradictory proposition and a fallacy.
This paper is organized as follows.Section 2 provides a brief account on how the concepts of actual and potential infinities have evolved throughout the history.Section 3 looks at an example that demonstrates how these two types of infinities can lead to completely different outcomes.Section 4 compares these two types of infinities and examines how applications of mathematical induction should be restricted and in which way the system of modern mathematics employs both“potential infinity=actual infinity” and “potential infinityactual infinity” depending on when one but not the other is needed.Section 5 investigates the impact of assuming potential infinityactual infinity on the development of mathematics.Then this paper is concluded in Section 6 with potentially important questions for future research along the lines depicted here.
2 The concept of infinity:as seen through the eyes of history
At the start of the recorded history scholars did not treat infinity as a mathematical object.Even so,they still comparably considered the concept in their works.For example,in geometry,recognized is the existence of a line or a plane[1]that extends indefinitely away from the origin,representing a potential infinity.Although these scholars did not explicitly claim this as an infinity-based concept,they indeed needed such an infinite framework for them to perform their investigations.
Parallelly,throughout history various mathematicians acknowledge that they did involve the concept of infinities either directly or indirectly because they work in a kind of infinite framework[2].Beyond such indirect recognition of infinities,the concept in fact has blatantly permeated the fields of mathematics and philosophy for centuries.For example,Aristotle(1984)clearly separates actual and potential infinities by realizing that when time is involved,a point implies the infinitude of actual infinity,while the infinitude of potential infinity appears over time.He believes that one accepts infinity solely on potential grounds,and all infinity-related failures stem from the invalid concept of actual infinities.In terms of our modern language,Aristotle defines a potential infinity as a forever ongoing and never-ending process of counting or measurement.In the contrast,Descartes[3]associates the actual infinity,mathematical infinity and meta-physical infinity one way or another.He and his followers believe that infinitude takes logical and epistemological precedence over the finitude.Pierre Gassendi(1592-1655)maintains Reference[3]that understanding infinitude is equivalent to understanding the negation of the finitude.Differently,Hegel[4]discounts Aristotelian thought by favoring a metaphysical infinity over a mathematical one.
As time enters the nineteenth century,mathematics heavily emphasizes set theory and the concept of infinite sets[5-6],on which the existence of actual infinities is explicitly introduced the first time in history.For example,Bolzano believes that to understand an infinite set,one simply needs to know the pattern its elements follow.Then,L.E.J.Brouwer[7-8]faces great discontent in Cantor′s work when he tries to revive Aristotelian view of infinities,where Cantor sees the totality of real numbers as a completed whole,an actual infinity.To this end,Henri Poincare perceives Cantor′s set theory as“a perverse pathological illness that would one day be cured”[9].

By applying Aristotle′s claim to calculus,one can readily see that the concept of actual infinities saturates the entire development of calculus,although it is not well acknowledged.In particular,all calculus-based concepts that involve actual infinity would be seen in Aristotle′s eyes as attempts that result in invalid applications of infinity.That represents a case where Hegel and Aristotle agree because when infinite sums and similar concepts are dealt with,calculus really talks about finite quantities.In particular,completing infinite many tasks within a finite amount of time is fundamentally the same idea as taking a limit.Thus,actual infinity regularly appears in calculus but is not paralleled with potential infinity so that these two different types of infinities are ambiguously blended.
Related discussions and debates have continued in our modern day.For example,Hailperin[15]formally characterizes a potential infinite sequence as a rule-generatable sequence.Hailperin[16]studies potential infinite verity functions defined on potentially infinite sequences.By introducing potential infinite models,he proved the fundamental theorem of potential infinite semantics along with several other important results.Engelfriet and Gelsema[17]investigate the concept of middle congruence,in which replication of a process is viewed as a potentially infinite number of copies of the process in the sense that copies are spawned at need rather than produced all at once.These authors develop laws to model!P as an actual infinite number of copies of P and their concept of middle congruence shares with standard congruence the suggestion that replication is only “potentially” infinite.By rigorously comparing actual and potential infinities,it is shown[18]that the foundation of mathematics is currently facing another important crisis.At the same time,Lin and colleagues[19]propose a plan to resolve this crisis by addressing how to select an appropriate theoretical foundation for modern mathematics and the theory of computer science and how to choose an interpretation so that the known achievements of mathematics and computer science can be kept in their entirety.Related to this attempt,developed recently are the internal set theory[20],the nonstandard set theory[21-22]and the Kawai[23]set theory.Kanovei and Reeken[24]look at which transitive ε-models of the ZFC can be extended to models of a chosen nonstandard set theory.The essence of these works is that one can employ nonstandard models to interpret such basic notions as infinitesimals and infinitely large quantities of the mathematical analysis of the 17th and 18th century.
Enriching the literature,this paper identifies the concept of endlessness with that of potentiality and the lack of completion,and the concept of wholeness with that of actuality and a full completion.With these two types of infinities clearly identified,the origin of infinity′s paradoxical nature can be readily seen,and important paradoxical aspects of mathematics and philosophy will consequently dissipate.
3 How actual and potential infinities can lead to different consequences
The brief review of literature in the previous section listed some scholars throughout the history,such as Aristotle,Descartes and Hegel,who unambiguously separated potential infinities from actual ones or only recognized one of these two types of inf i nities.Hence,the following question naturally arises.In mathematical reasoning,are there situations where these two different kinds of infinities practically lead to different numerical consequences?The answer to this question is a definite YES.Before seeing other possible scenarios that answer this question with a YES outcome,let us first quickly review the following example from References[25-26].
Consider a container and pieces of paper.Assume that there are infinitely many of them,each of which is labelled by one and only one natural number starting from 1,2,3,···.Let us now place the pieces of paper with labels 1 to 10 into the container and then take out the piece with label 1.Recursively,at step n,we place the pieces of paper with labels 10n-9 through 10n into the container and then take out the piece with label n,for any natural number n.When this process is completed,how many pieces of paper will be left in the container?

As shown by Lin[25],in the construction of this example the size of the container and the total area of the pieces of paper can be any predetermined values.And of course,in theoretical discussions,the terms “container” and “pieces of paper”are symbolic and imaginary so that there is no need to think about size and area.
The discussion above surely leads to the following natural question:Should actual and potential infinities be the same or different from each other?
4 Comparison between actual and potential infinities
The history can be coarsely treated as two periods:the enlightenment period and a modern period.The earlier period lasted for over two thousand years,where scholars recognized the difference between actual and potential infinities,while the latter one started about one hundred plus years ago,during which the boundary between these two types of infinities becomes blurred.However,the previous section suggests that actual and potential infinities should not be assumed to be the same.In this section,we examine what happens in two separate cases:
4.1 Actual infinity=potential infinity
One of the most widely used principles,under which actual infinity=potential infinity,is mathematical induction.After successfully confirming both the initial and inductive steps,the proposition of concern is believed to hold for either(i)every natural number n or(ii)all natural number n.As can be seen readily,case(i)stands for a potential infinity,while case(ii)an actual infinity.It is because the former represents the ongoing and never-ending process of enumerating natural numbers one by one—a present progressive tense,while the latter indicates that the elements in the entire set of natural numbers has been exhaustively carded through—a perfect tense.Intuitively,we can imagine the process of using mathematical induction as looking at a ladder of infinite length.The initial and inductive steps mean that first we can get on the ladder,and second if we are on step k of the ladder then we can climb onto step k+1.That is,these steps jointly stand for enumerating natural numbers one by one without mentioning whether or not such enumeration can be exhausted or completed.However,in modern mathematics,both conclusions(i)and(ii)are used interchangeably without any distinction.And since,as is known,a present progressive tense and a perfect tense are different of each other,any proof based on mathematical induction,a potential infinity,cannot naturally lead to a conclusion of an actual infinity.For such a jump to occur,modern mathematics must have implicitly assumed that potential infinity=actual infinity.
In terms of the historical development of mathematical induction,Plato′s Parmenides of 370 BC[27]contained an implicit inductive proof.And related idea can also be found in Euclid′s proof that the number of primes is infinite.Another early trace of mathematical induction can be found in Bhaskara′s,an Indian mathematician and astronomer,cyclic method[28].A proof using mathematical induction was introduced in the Al-Fakhri fi′l-jabr wa′l-muqabala(Glorious on algebra)written by al-Karaji,a 10th century Persian Muslim mathematician,around 1000 AD.In this work,the principle of mathematical induction was used unconsciously to prove the binomial theorem and properties of Pascal′s triangle without explicitly stating the inductive hypothesis.Similar situation occurred with Francesco Maurolico when he wrote Arithmeticorum libri duo(1575),where mathematical induction was implicitly employed to prove that the sum of the first n odd integers is n2,with Pierre de Fermat(1601-1665)and with Jakob Bernoulli(1654-1705).Then in 1665 Blaise Pascal explicitly formulated mathematical induction in his Trait´edu triangle arithm´etique(1665),while the present rigorous and systematic treatment of the principle came only in the 19th century with George Boole(1815-1864)[29],Charles Sanders Peirce(1839-1914)[30],Giuseppe Peano(1858-1932)(the Peano axioms,see his book of 1889,entitled The Principles of Arithmetic Presented by a New Method),and Richard Dedekind(1831-1916)[29].
4.2 Actual infinitypotential infinity
Contrary to the previous discussion,this subsection examines a situation that exists in the system of modern mathematics where actual infinity is not seen as the same as potential infinity.

Let P be a predicate,denote the contrary opposite of P asP and the contradictory opposite of P as◁P.Then,the law of proof by contradiction can be expressed as:where A is the proposition that needs to be shown,and the set of premises,such as the starting axioms and/or theorems established earlier.If A or◁ A within Γ leads to B,then we conclude that based on the premises in Γ,◁ B leads to ◁ A or A itself,respectively.The union symbol is used here for sets of statements in such a way that it is more related to logical conjunction(and).
Within the system of modern mathematics,where the two-valued logical calculus is employed,the law in equation(1)leads to the principle of excluded middle and that of no contradiction:

In the two-valued logical system of modern mathematics,the contrary opposites(P,P)are seen as the same as the contradictory opposites(P,◁ P)so thatP=◁P.Because potential infinity(poi)and actual infinity(aci),as the opposites in a pair of contrary opposites(P,P),must now be a pair of contradictory opposites(P,◁ P),poi and aci must respectively stand for the affirmative and the negative aspect of a concept and have to satisfy the principles of the excluded middle and no contradiction:which means that poiaci.In other words,the system of modern mathematics has conventionally implemented the following inequality:potential infinityactual infinity.
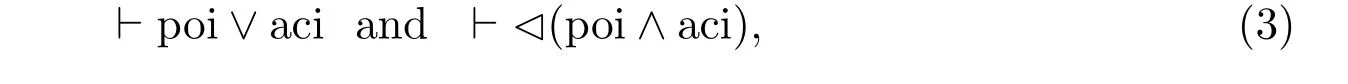
To summarize,what are discussed in this section implies that the system of modern mathematics implicitly assumes both “potential infinity=actual infinity” and“potential infinityactual infinity”.For related discussions,see Reference[34].
5 Impacts of actual infinitypotential infinity on modern mathematics
Discussions above strongly suggest that actual infinitypotential infinity or that the conclusion “the proposition Φ(n)holds true for all(or for every)natural number n” of mathematical induction should be limited to the use of“for every”.In particular,the phrases “for all” and “for every” are different from each other.And quantitatively,these different phrases can produce different answers.
Evidently,such a one-word adjustment will affect mathematics a great deal,because,for example,most constructive proofs of existence tend to be mathematical induction based so that they need to be re-established.In particular,each such proof f i rst demonstrates the validity of a non-terminating process—a potential infinity,and then claims that an actual infinity has been obtained.One example to this end is the constructive proof for that every bounded sequence of real numbers has a convergent subsequence,where the construction of a subsequence appears as a potential infinity,while the existence of the eventual subsequence stands for an actual infinity.Another example is the constructive argument for that the set of all real numbers has an uncountable cardinality,where a decimal number is constructed one digit a time—a potential infinity,and then the existence of an imagined decimal number,assuming that the forever ongoing progressive procedure of constructing digits one by one can be completed,is claimed—an actual infinity.
In the rest of this section,we look at how modern mathematics deals with the concepts of potential and actual infinities either interchangeably or not.For related discussions,see Reference[31].
Based on discussions above,it can be readily seen that both Cantor and Zermelo employed the logical reasoning of actual infinities in both naıve and axiomatic set theory,while Cauchy and Weierstrass applied that of potential infinities in the development of limits.However,the logical reasoning of actual infinities has not been applied consistently in set theory,while that of potential infinities not utilized congruently in the theory of limits,either.
In particular,each infinite set A={x|P(x)},as studied in set theory,consists of all elements x,each of which satisfies the given proposition or condition P.So,the existence of A represents an actual infinity,while checking whether particular elements belong to A is a potential infinity.That is,surprisingly to both Cantor and Zermelo,even the modern version of the axiomatic set theory,such as the ZFC,involves not just solely actual infinities but also potential infinities.In fact,the expectations of Cantor and Zermelo is impossible to materialize.For example,from Cantor to Zermelo,the idea of one-to-one correspondence appeared everywhere.Just as what is pointed out in Subsection 4.1,when this idea is employed onto infinite sets,each one-to-one correspondence represents a process of enumeration.Before the process is exhausted and completed,it is forever a present progressive tense(or a never-ending ongoing procedure).Therefore,each one-to-one correspondence corresponds to or represents a potential infinity.In other words,the modern axiomatic set theory itself—specifically the ZFC set theory,is really a system that is developed on the thinking logics of both actual and potential infinities,instead of a system completely implementing the concept of actual infinities without touching on that of potential infinities,as expected by Cantor and Zermelo.
As for the theory of limits,to prevent the Berkeley paradox from occurring,any direct employment of both actual infinities and actual infinitesimals is avoided through using the ε- δ and ε-N methods.Specifically,both actual infinities and actual infinitesimals are replaced by forever progressive procedures of going beyond any indefinitely given bounds,while the final or limiting states(or values)of the procedures represent actual infinities,a situation similar to what is described in Section 3.
Specifically,as the foundation of calculus and mathematical analysis,although the theory of limits employs the methods and language of ε-δ and ε-N to replace the usage of the concepts of infinities and infinitesimals,the process of applying these methods represent a non-terminating present progressive tense(or never-ending ongoing process)of choosing a bound and going beyond that bound and choosing another bound and going beyond this new bound.Hence,the ε-δ and ε-N methods themselves directly face with the logical reasoning of potential infinities.In particular,for the situation that a variable x approaches its limit x0,the presently accepted convention is not to mention whether x can or cannot materially reach the limit point x0.Instead,what is used is the expression 0 < |x-x0|< ε.That is,there is the possibility that the variable x indefinitely approaches its limit point x0and will not reach point x0.Hence,the concept of limit for a variable x to approach a limit point x0represents a present progressive tense(or a never-ending ongoing process)instead of a perfect tense(or a process with a definite end).That is,the theory of limits heavily implements the logical reasoning of potential infinities.However,as it turns out,this theory cannot totally avoid the logical reasoning of actual infinities,either.For example,when an irrational number is written analytically,the spirit of actual infinities emerges,because behind the decimal point,each irrational number contains an infinite number of digits.So,for this irrational number to exist,the never-ending string of digits after the decimal point has to end—a situation where an actual infinity not only appears,but also is forced to equal an potential infinity.Beyond this particular situation,when calculus is developed on the theory of limits,discussions have to be generated on the actually infinite field that is one way or another made up of the set of all real numbers.Therefore,we conclude that the theory of limits is a theoretical system that is based on the logical reasonings of both actual and potential infinities.
Summarizing what has been discussed above,it can be readily seen that the development of modern mathematics has assumed both the equation that actual infinity=potential infinity and the inequality that actual infinitypotential infinity.Hence,revealed here is another paradox that is deeply rooted in the thinking and logical reasoning of modern mathematics.At this junction,one interesting and important question is the following.What would happen to the Berkeley paradox and Russell′s paradox in the lens of actual and potential infinities?
6 A revisit to the Berkeley and Russell′s paradoxes

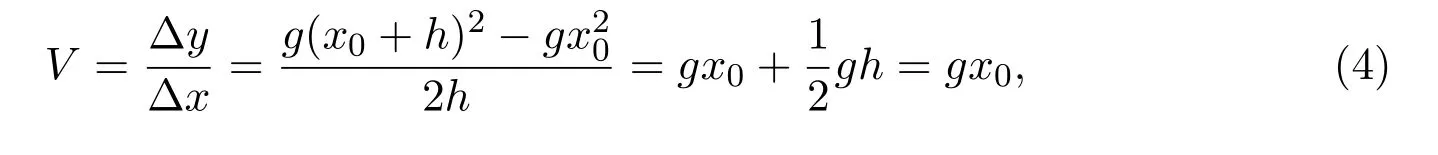
However,no matter how close h(0)is to 0,the last equality in equation(4)does not hold true,making V become the meaningless 0/0.That is,in general,there is no way to compute the derivative of the given function at any specified point x0.Although both Newton and Leibniz provided several explanations to overcome this difficulty[2],they cannot satisfactorily make people feel the following contradiction has been resolved.To make V=meaningful,one has to have h0;and to produce the desired derivative V=gx0,one must assume h=0.The well-known Berkeley paradox is that to find the derivative of y=at point x=x0,one has to force a none-zero variable to be zero.
After the concept of limits was introduced,the Berkeley paradox was“successfully”resolved as follows:

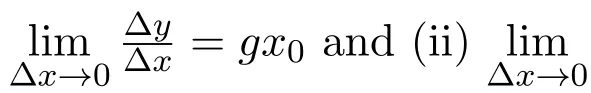
The expression Δx → 0 in equation(5)is supposed to mean the same idea.However,when it is applied to expression(i),it stands for a forever progressive process without any end—a potential infinity.And when it is applied to expression(ii),it represents an actual infinity with a definite end.So,a natural question appears as follows.For the same process of solving the same problem and for the same expression Δx→ 0,how can the variable Δx be allowed to approach 0 in either a potential fashion or an actual fashion depending on the researcher′s will?Evidently,allowing such deduction and reasoning is hard for people to feel content.In short,as long as the concepts of approaching limits in the fashion of either actual or potential infinities are distinguished from each other,calculus will still be living in the shadow of the Berkeley paradox.
To conclude this section,let us now turn our attention to the Russell′s paradox[32],details of which are outlined as follows to make this paper self-contained.Divide the totality of all sets into two classes X and Y such that

and let Z be the set of all sets such that Z={s|s is a set and s/∈s}.Question:Which of Z∈X or Z∈Y holds true?Based on the given setup,either Z∈X or Z∈Y needs to be true.If Z∈X,then the definitions of X and Z imply both Z∈Z and Z/∈Z,a contradiction.If Z∈Y,then definitions of Y and Z imply both Z/∈Z and Z∈Z,which is also a contradiction.
Theorem 6.1The Russell′s paradox is a self-contradictory proposition and a fallacy.
Proof For an object or proposition X,let¬X stand for the negation of X,X¬X a proposition that is self-contradictory,and X¬X ↔ Ø,where↔ means“is equivalent to”,the judgmental conclusion that the self-contradictory proposition X¬X is a fallacy,meaning that X¬X is a recognized incorrect proposition.Then the law of contradiction of the classical logic can be expressed as follows:
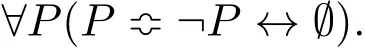
Let Y={s|s/∈s}and¬Y={s|s∈s},where s is simply a collection of elements.That is,each s does not have to be a set as defined in the ZFC axiomatic set theory.Then the analysis above implies(Y∈Y)↔(Y/∈Y)and(Y/∈Y)↔(Y∈Y).Define I=(Y∈Y).Then¬I=(Y∈¬Y)=(Y/∈Y).Hence,I¬I↔Ø.That is,the conclusion of the theorem follows.QED
For additional discussions on various paradoxes,see Reference[13].
7 Some final words
What are obtained in this paper vividly demonstrates that there are much to be done in the foundations of mathematics and related fields,where the logical reasonings of actual and/or potential infinities are employed either explicitly or implicitly.For example,all paradoxes or antinomies that are known in areas of philosophy and mathematics need to be revisited by using the assumption that actual and potential infinities are different from each other and by clearly distinguishing theoretical descriptions and judgments.All known conclusions developed by treating “for all” and “for every” indifferently need to be unsympathetically reestablished.All results that are derived by assuming actual infinity is the same as potential infinity need to be re-evaluated and see what will happen if these two types of infinities are assumed to be different.
Our discussion in this paper suggests that there might be two systems of mathematics.One of them assumes that actual infinities are different of potential infinities;and the other bases on the assumption that these two types of infinities are the same.
