Hardy空间上的复对称C0-半群*
2022-01-23吕新莹
吕新莹
(天津大学数学学院,天津 300354)
0 引 言
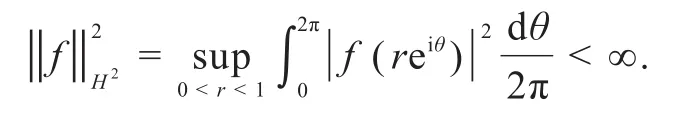
令ψ是D上的全纯函数,ϕ是D上的解析自映射,对于∀f∈H2(D),z∈D,ψ,ϕ诱导出H2(D)上的一个线性加权复合算子Wψ,ϕ,定义如下
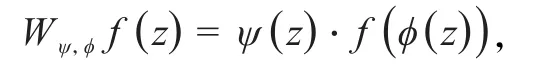
当ψ≡1时,加权复合算子Wψ,ϕ便是复合算子Cϕ.
本文主要研究Hardy空间上的复对称C0-半群,先给出一些基本定义和概念.
(1)T(0)=I,其中I为X上的恒等算子;
下面定理是本文的核心结论.对于H2(D)上C1-对称的强连续加权复合算子半群,不妨假设ϕt(z)为非常值分式线性映射,若ϕt(z)恒为常数,结论显然.
(1)ϕ0(z)=z,对于∀z∈D;
注为了方便讨论,先列举域Ω⊂C内的解析自映射半群的2个性质,会在下文一直使用:(1)对于所有t≥ 0,映射z↦ϕt(z)是单射;(2)对于所有z∈Ω,映射是解析的 .关于更多解析自映射半群性质的介绍见文献[1].
定义0.3设为半群,若存在是D上的一族全纯函数,且满足,使得
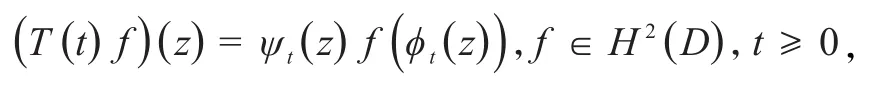
患者仰卧位平躺于体架上,双手交叉于头顶,热塑体膜于恒温水箱软化,覆盖在患者体表固定体位,待20 min左右检查塑形状况,确认塑形好后取下[5]。
定义0.4设H是一个可分的Hilbert空间,C是H到自身的映射.若C满足:
(2)C2=I;
则称C是H上的一个共轭.设T为H上的有界线性算子,若存在H上的一个共轭C使得T=CT*C,则称T是复对称算子.
定义0.5[2]设为H上的C0-半群,若存在一个与t无关的共轭C使得则称是C-对称的C0-半群 .
下面给出分式线性映射的定义和分类.
分式线性映射是形如
对研究对象临床上的影像学特点进行回顾与分析,跟临床的检测结果进行对比。对两组研究对象之间确诊的概率进行对比。
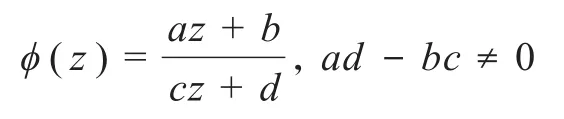
的映射.若存在z0∈D,有则称z0是ϕ(z)的不动点.若ϕ(z)在D内没有不动点,则存在τ∈∂D满足,且其中τ称为ϕ的 Denjoy-Wolff点,dϕτ为映射ϕ在点τ处的微分,也称为切映射,是ϕ的边界伸缩系数.
根据其不动点的位置与个数可知D上的分式线性映射半群分为以下 3 种类型[1]:
又因为α∈∂D,因此则 有k=且k满足
(2)如果ϕ1在D内没有不动点,τ∈ ∂D是ϕ1的Denjoy-Wolff点,若ϕ1是双曲型的分式线性映射,那么就叫做一个双曲型分式线性映射半群;
(3)甲房地产企业为一般纳税人,对开发项目采取一般计税方法计税。为开发某项目,该公司取得一块面积为15万平方米的土地,支付土地出让金3 000万元(取得财政部门收据),该项目总面积39万平方米。项目完工后,公司将部分房产对外销售,取得含增值税收入10 000万元,对应建筑面积10 000平方米,房屋已经交付业主并开具增值税发票。
(3)如果ϕ1在D内没有不动点,τ∈ ∂D是ϕ1的Denjoy-Wolff点,若ϕ1是抛物型的分式线性映射,那么就叫做一个抛物型分式线性映射半群.
关于加权复合算子半群的复对称性的研究历史并不是很长,最早是Hai和Khoi[2]提出了复对称C0-半群的概念,并进一步刻画了Fock空间中加权复合算子的复对称C0-半群;Wang和Han[3]研究了右半平面上Bergman空间中的加权复合算子的复对称C0-半群.迄今为止,对加权复合算子的复对称C0-半群的研究结果并不多,甚至连经典的H2(D)上关于加权复合算子的复对称C0-半群还没有给出刻画.
证明 当ϕt(z)有内部不动点a≠0时,令ζt=ϕa◦ϕt◦ϕa,于是有ξt(0)=0,其中从而
本文根据单位球上分式线性映射半群的不动点的位置及个数对分式线性映射半群进行分类的结果[1,7-8],结合定义 0.1 给出H2(D)上加权复合算子关于C1-对称时的形式,完整地刻画了H2(D)上C1-对称的强连续加权复合算子半群的具体形式.
下面定理给出H2(D)上加权复合算子关于C1-对称时的具体形式.
定理0.1[6]令ψ是D上的全纯函数,ϕ是D上的解析自映射,使得加权复合算子Wψ,ϕ满足Wψ,ϕ:是由u,ν诱导的共轭算子,其中则Wψ,ϕ是C1-对称的当且仅当其中,C0,C1∈D,d∈ C.
结合定义0.1以及强连续加权复合算子半群的定义0.3,易得如下结论.
本文利用墨尔本大学Rajkumar Buyya教授开发的Cloudsim-3.0.3云计算仿真平台[8],测试本文提出的云计算资源调度方法的有效性.实验中考虑了资源的处理速度和待处理任务的长度,以不同规模的资源请求环境下任务的完成时间作为评价指标.具体参数设置为:种群规模为30,计算资源数量为10,学习因子c1、c2均为1.2,权重值wmax和wmin分别设定为0.9和0.4.
引理 0.1设C1:=Au,ν是由u,ν诱导的共轭算子 ,这 里若是H2(D)空间上C-对称的强连续加权复合算子半群,定义为则分 别 满 足 如 下 形 式 :是D上的一个半群,满足0,这里C0t∈D,C1t∈D,dt∈C.
相似度比较计算是信息分类及判别的关键技术。由于自然语句是由字、词语及关键字等组成,相似度的比较计算可以分为词语相似度、语义相似度、句子相似度、句长相似度等多个特征方面。其中,词语相似度是指两个或几个词语所表达的内涵相同或相近,可以互相替换使用而不改变整个语句的文义的程度,常用的词语相似度算法有基于统计和基于规则的两种方法;句子相似度主要由基于语法的分析和基于词汇相似度矩阵的分析方法。通过多个特征相似度的分析计算,对语句及其含义进行综合对比研究,从而达到自动评阅的目的。
1 主要结论及证明
(2)T(t+s)=T(t)T(s),∀t,s≥ 0;
定理 1.1设C1:=Au,ν是由u,ν诱导的共轭算子 ,这 里是H2(D)→H2(D)的强连续加权复合算子半群,则是C1-对称的当且仅当以下任一条件成立:
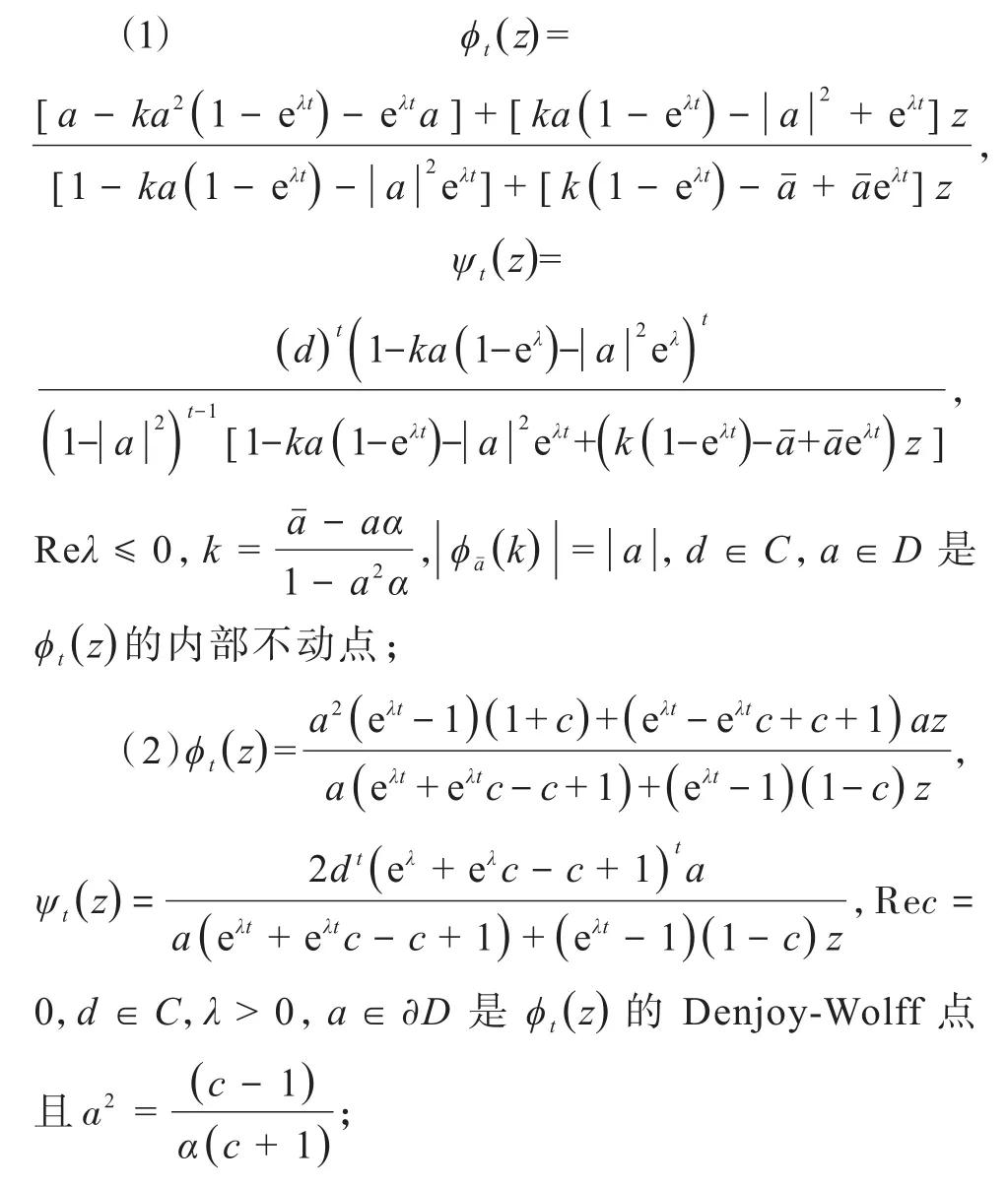
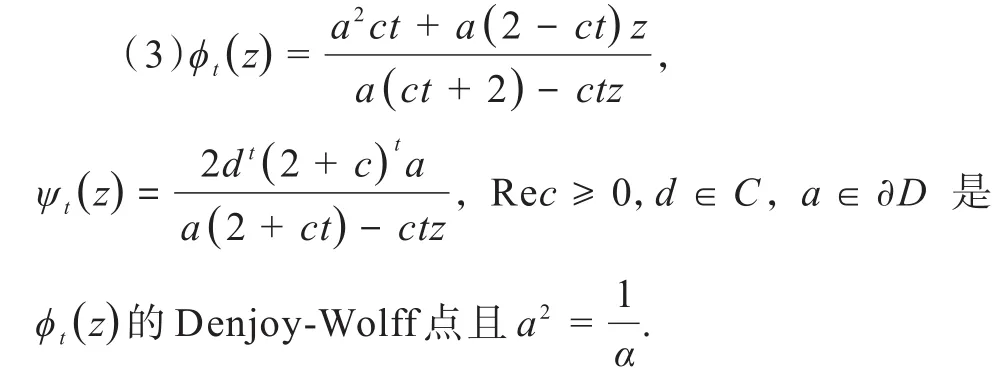
注对比于引理0.1,当ϕt(z)的内部不动点a=0时,对于满足条件(1),是C1-对称的;当ϕ(z)的内部不动点a≠0且a∈D时,对于∀β∈∂D,只有当时满足条件(1)是C1-对称的;当ϕt(z)无内部不动点时,对于∀β∈ ∂D,只 有 当或时,满足条件(2)或(3)是C1-对称的.
接下来,根据D上分式线性映射半群的类型,分3种情况来证明定理1.1的充分性.
引理1.1若ϕt(z)与ψt(z)满足引理0.1的条件,且(ϕt)是以a为不动点的椭圆型分式线性映射半群,则有
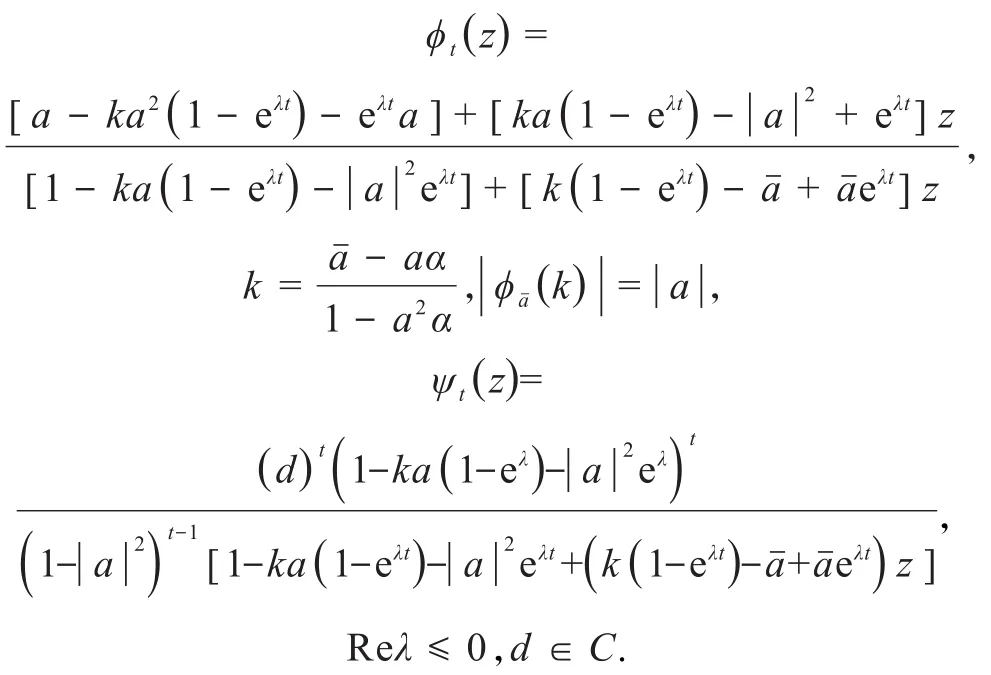
对于Hilbert空间上加权复合算子的复对称性的研究,目前已经有了比较完整的结论.最早是Jung等[4]给出了Hardy空间上关于特殊共轭Jf(z)=复对称的加权复合算子的具体形式;Hai和Khoi[5]给出了Fock空间上关于更一般的共轭复对称的加权复合算子的具体形式;Lim和Khoi[6]研究了Hardy空间上关于一般共轭复对称的加权复合算子,并将其分为了C1-对称和C2-对称2类,关于C1-对称的结果见定理0.1.
安:只要你对音乐足够敏感,就不难发现,格里格的音乐也好,其他杰出作曲家的音乐也罢,都是具有普世性的。如果按照所谓“文化差异”的观点,那么郎朗怎么可能演奏好来自巴西的桑巴舞曲呢?但其实郎朗很擅长弹奏桑巴!当然还有西班牙音乐,以及其他民族、文化的音乐。又比如,吉列尔斯与霍洛维兹又是如何弹奏好斯卡拉蒂和克列门蒂的作品呢?他们虽来自俄罗斯,但却把意大利的作品弹奏得如此精彩!德彪西又是如何在没去过亚洲与西班牙的情况下写出《版画集》的呢?因此,杰出的音乐和艺术家总是具有相似的普世性。
锁相放大器是微弱信号检测领域中是一种基于相关检测理论的对交变信号进行相敏检波的放大器,能对检测信号和参考信号进行相关运算,有效地抑制噪声,实现对信号的检测和跟踪[7-8]。基本原理如图2所示,主要由被测信号模块,参考信号模块,相敏检测和低通滤波器等几部分组成[1]。
对于Bt+s=BtAs+Bs,两边关于s求微分,并令s=0得
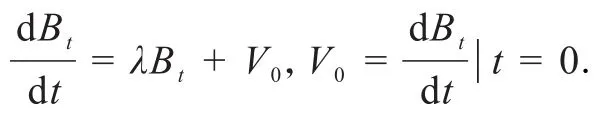
根据B0=0 可解得则有
此时
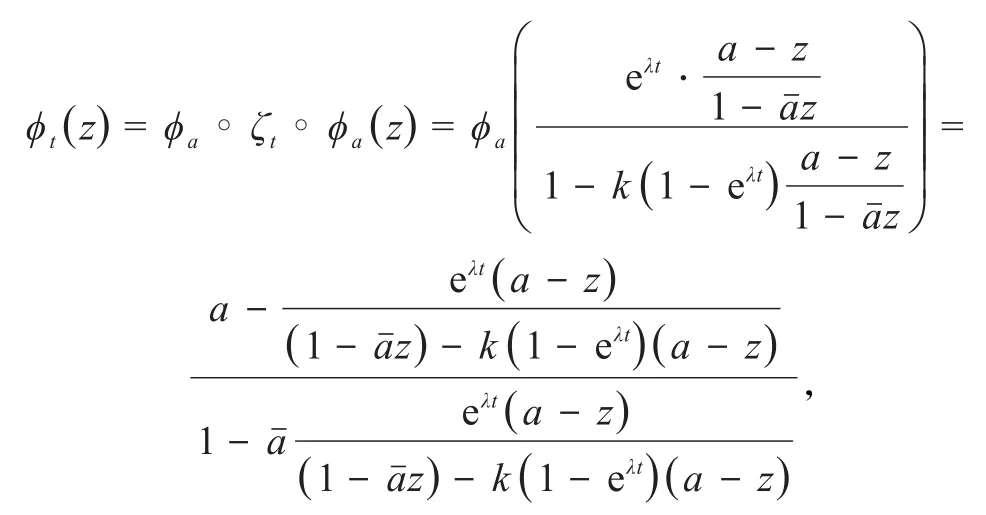
整理得
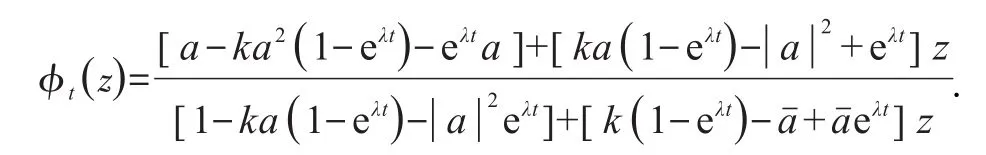
令z=0,有经计算易得
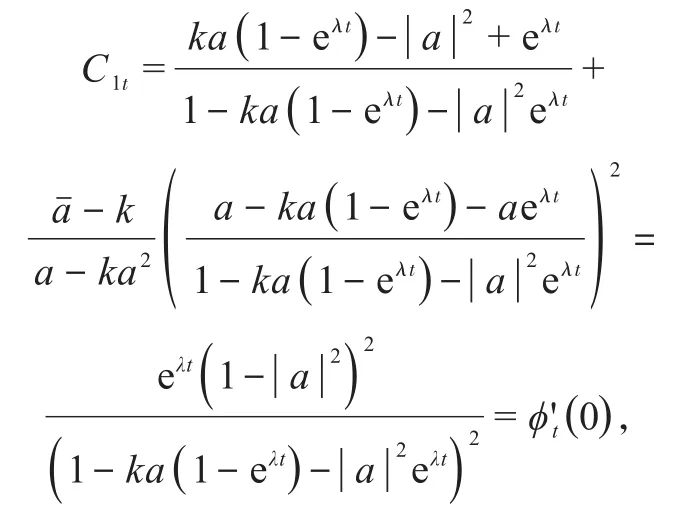
此时
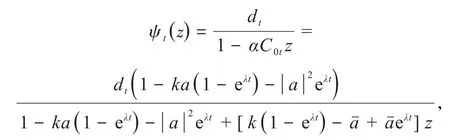
(1)如果ϕ1在D内有唯一的不动点,那么就叫做一个椭圆型分式线性映射半群;
现在问题转化为计算dt的形式,记根据令z=a可得即当f恒为常数,z为 0 时,由{Tt}的强连续性可知dt是连续的,从而ht连续.
事实上,对于连续函数f,若f(m)f(n)=lf(m+n),则当m为整数时,有当m为有理数时,有当m为无理数时,由连续性有所以,对于 ∀m,n≥ 0,f(m)=因此
Hr=[Re(Hc),-Im(Hc);Im(Hc),Re(Hc)],Hr为实数域模型中的信道传输矩阵,Hc为复数域模型中的信道传输矩阵;Xl,s为2Nt× 1的矩阵Xl,s=[Re(xl,s);Im(xl,s)],Xl,s中只有两个非零元素;噪声N为2Nr× 1的矩阵,N=[Re(n);Im(n)].其中Re()和Im()分别表示取得•的实部和虚部.本文后面的H均表示实数域模型中的信道矩阵.
比如美国。2015年9月5日举行了第15届国家阅读节,主题是“我的生活里不能没有书”,国会图书馆邀请175位作家、诗人与读者共襄盛举。除了阅读节,美国还把儿童文学作家苏斯(Dr.Seuss)的生日3月2日定为全美诵读日,每年都有数千万人参与阅读与朗诵的活动。
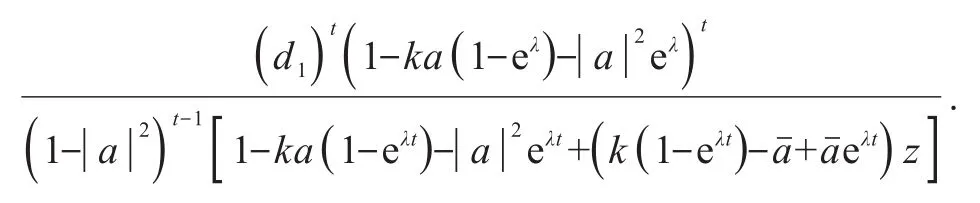
特 别 地,当a=0时,有则 存 在λ,Reλ≤ 0 使得此时eλt,α∈ ∂D且ψt(z)=dt,又 由得,dt+s=dtds,由上述证明过程可知ψt(z)=d1t;当a=0 时,k=0.综合以上 2 种情况令d=d1即证.
引理1.2若ϕt(z)与ψt(z)满足引理0.1的条件,且是双曲型分式线性映射半群,设a为其Denjoy-Wolff点,则有
为了保障航运业的需求,中国炼油企业应改变被动观望态度,积极主动地做好低硫燃油的生产工作安排。在经济性测算的基础上,根据自身装置情况,强化技术研发,提前与燃油供应商、航运公司绑定供应需求。
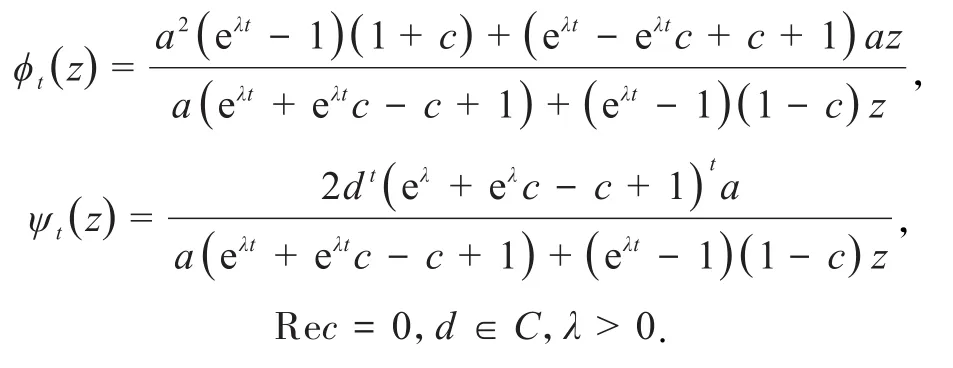
证明设且ϕ(1)=1,则a+b=c+d.此时,令ϕ0=σ◦ϕ◦σ-1,其中为凯莱变换,H为右半平面,易得
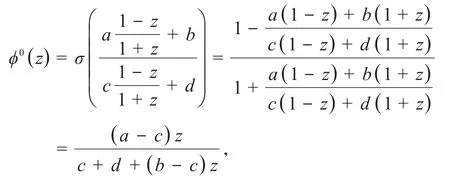
分式上下同时除以c+d有记有此 时 令G:H→H,此时ϕ1:H→H,且有
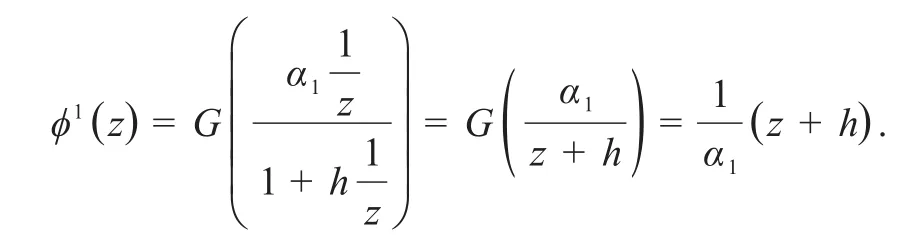
结构的维持对于功能的发挥至关重要,在周围神经再生的进程中,首先最重要的就是轴突再生通道以及微环境的建立。3D打印技术已在血管[32]、骨修复材料[33]和软骨修复材料[34]等多个领域取得了成功,目前刘小林团队[35]运用猪去细胞神经细胞外基质成分制作水凝胶来修复大鼠坐骨神经缺损,取得了与去细胞神经移植物非常接近的实验效果,其研究成果极大的促进了3D打印神经修复材料的进步。若3D打印的周围神经可以克服目前管腔中空神经导管的不足,在精细结构和成分上与正常神经更为接近,必将推动周围损伤修复材料的进一步发展。
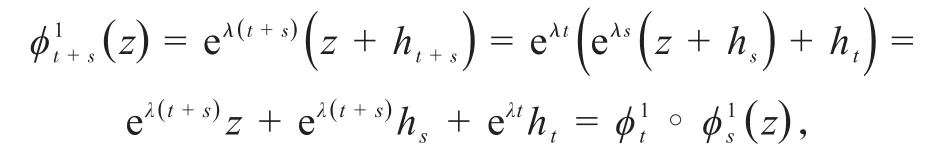
记qi=npi/p,ni-=[qi](下取整),ni+=ni-+1,bi=qi-ni-.将剩余资源优先分给尾数bi最大的部门的分配方法称为哈密顿法(Hamilton法)[2].
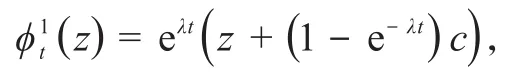
注意到Reht≥0,则有Rec≥0.
经济基础影响和决定着社会的物质生活、精神生活等各个方面,而且它又反过来必须以社会生产力的发展为前提。早期的以畜牧业为主的青海卫拉特蒙古社会,饮食内容和方式上也同样体现了其社会生产特征,饮食种类也比较朴实、单一和粗放。
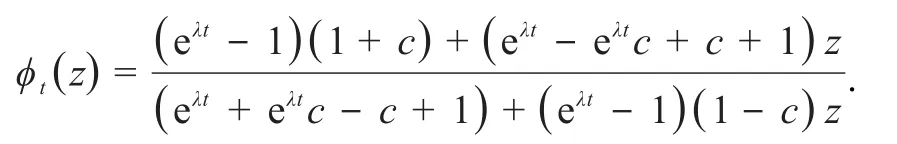
对于更一般的情形a∈ ∂D,存在以1为不动点,即
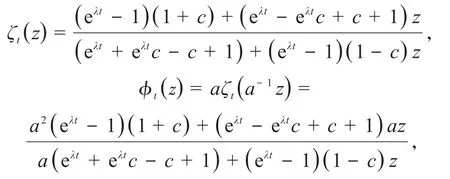
且通过简单计算可得ϕt(z)有2个不相等的不动点
与引理1.1的证明类似,令z=0得C0t=进一步可得又 因 为α∈ ∂D,因 此Rec=0.此时ϕt(z)有2个不相等的边界不动点.将α和C0t代入ψt(z)可得
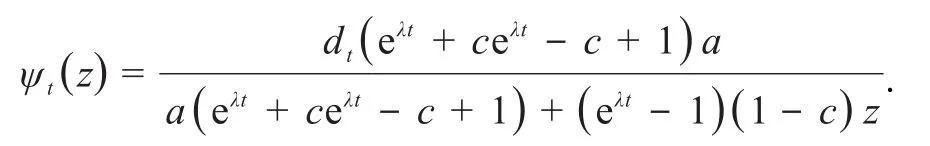
现在计算dt的形式,为方便起见,记根 据当z=a时,有,同引理1.1可得将dt代入ψt(z),令则有
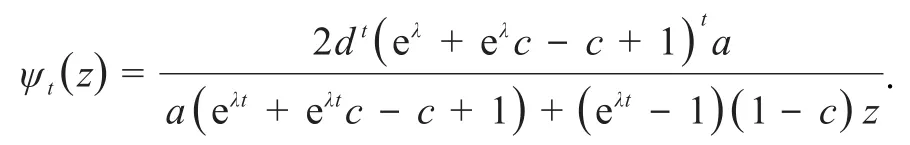
综上,引理1.2得证.
引理1.3若ϕt(z)与ψt(z)满足引理0.1的条件,且(ϕt)是抛物型分式线性映射半群,设a为其Denjoy-Wolff点,则有
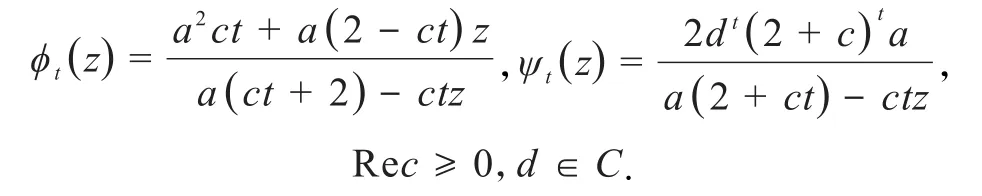
证明若ϕt(z)为抛物型分式线性映射半群,由文献[1]的定理1.5或6.1可知
当a=1时,对引理1.2证明过程中的G,σ,此 时其 中Reht≥ 0,根据的半群性质可得从 而此 时 ,
对于一般情况,即以∀a∈∂D为Denjoy-Wolff点的抛物型分式线性映射半群,令则有ζt(1)=1,同引理1.2此时有
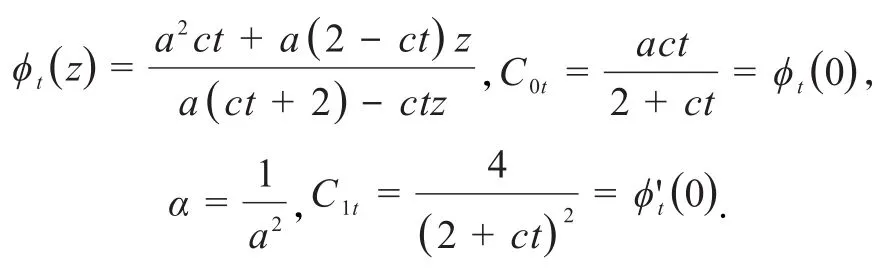
将α和C0t代入ψt(z)则有dt求法同上,有此时,令整 理 得
综上,定理1.1充分性得证.下证必要性.
