Integer quantum Hall effect in Kekul´e-patterned graphene

Yawar Mohammadi and Samira Bahrami

Department of Physics,Farhangian University,Tehran,Iran

Keywords: AAA-stacked trilayer graphene,integer quantum Hall effect,Kubo formula,Hall conductivity

1. Introduction

Space-modulated two-dimensional materials in which the lattice structure is modified by strain, twisting of the layers or the substrate, etc. are very interesting platforms for novel physical phenomena.[2-8]Recently,Guti´errezet al.[9]have revealed Y-shaped Kekul´e bond textures in a honeycomb lattice on a graphene-copper superlattice, in which one of the six carbon atoms in each superlattice unit cell has no copper atoms below it and acquires a shorter nearest-neighbor bond length. Gamayunet al.[10]have shown that such a bond texture locks the valley degree of freedom of the charge carriers to their direction of motion, resulting in the breaking of the valley degeneracy of graphene and the emergence of two species of massless Dirac fermion in Y-shaped Kekul´epatterned graphene.[10]Other works have explored the effects of Kekul´e textures on graphene;Wuet al.[11]proposed a type of valley field-effect transistor made from Y-shaped Kekul´epatterned graphene and explored tuning the valley pseudomagneto resistance via an electric field. Andradeet al.[12]studied the effects of uniaxial strain on the band structures of all types of Kekul´e-distorted graphene. Further works have investigated[13,14]the effects of Kekul´e textures on the electronic transport properties of Kekul´e-distorted graphene, as well as the consequences of Kekul´e distortion on the optical conductivity[15,16]and dynamical polarization of graphene.[17]

To date, most of the works on the topic of Y-shaped Kekul´e-patterned graphene have studied its properties in the absence of a magnetic field. It is, however, interesting to explore the effects of a Y-shaped Kekul´e bond texture on the magnetotransport properties. Moreover, the integer quantum Hall effect is one of the most intriguing properties of twodimensional electron-gas systems, in which the Hall conductivity in a strong magnetic field is quantized in integer multiples ofe2/h.[18]This effect has been observed in graphene,but with a different quantization that arises from its chiral massless Dirac-like spectrum.[19-21]Recently,several groups have studied the effects of the stacking order on the integer quantum Hall quantization of multilayer graphene.[22-27]In this paper, we address the effects of the Y-shaped Kekul´e bond texture on the quantum Hall transport properties of single-layer graphene. We derive an analytical expression for the Hall conductivity and find that the presence of the Y-shaped Kekul´e bond texture lifts the valley degeneracy of all Landau levels except that of the zero Landau level;this behavior is described by the Atiyah-Singer index theorem.[28]This leads to a new type of anomalous quantum Hall conductivity quantized asσxy=νe2/hwithν=±2,±4,±6,±8,.... We also obtain an analytical expression for the longitudinal conductivity,which,along with the analytical expression for the Hall conductivity,can be used to evaluate the Hall and longitudinal resistivities and to explore the effects of the Kekul´e bond texture on them.

The rest of this paper is organized as follows. In Section 2,we introduce the formalism used and obtain analytical expressions for the Hall and longitudinal conductivities. Section 3 is devoted to presenting the results and a discussion.Finally, in Section 4, we end the paper with a summary and conclusions.

2. Model and formulation

Figure 1(a)shows the lattice structure of a Y-type Kekul´epatterned graphene.According to the tight-binding model proposed by Gamayunet al.,[10]the low-energy Hamiltonian for Kekul´e-patterned graphene is given by

wherevFis the band velocity of pristine graphene,p=(px,py)is a two-dimensional momentum, andσ=(σx,σy) are Pauli matrices. Furthermore, ˜Δis the energy coupling amplitude originating from the Kekul´e bond texture andQν=vF(ν pxipy)σ0is the Kekul´e texture coupling between Dirac Hamiltonians, whereσ0is the identity matrix andν=±denote two types of Y-shaped Kekul´e texture.[10]For simplicity, we consider a real ˜Δ=Δ0andν=1. Note that complex ˜Δandν=-1 are equivalent upon a unitary transformation. In this model,the effects of bond modulation have been taken into account via the Kekul´e bond texture amplitude,Δ0. Therefore,the effect of the bond modulation on the quantum Hall effect in Kekul´e-patterned graphene can be examined by changingΔ0.

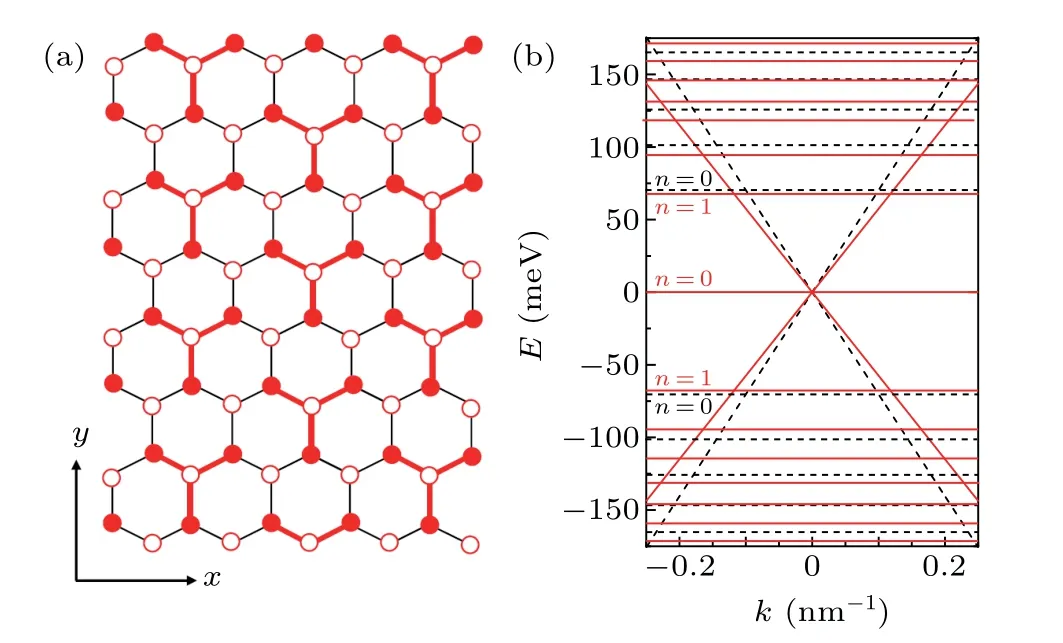
Fig. 1. (a) Schematic representation of a graphene Lattice with a Y-shaped Kekul´e texture. Thick red and thin black lines distinguish different bond strengths. (b)The solid red(dashed black)curves show the low-energy spectrum of its slow(fast) cone with a velocity of vF(1-Δ0) (vF(1+Δ0)) for a Δ0 =0.1 Kekul´e bond texture. The horizontal lines show the Landau levels for B=4 T.

2.1. Eigenvalues and eigenstates

The low-energy Hamiltonian of Kekule-patterned graphene in the presence of a perpendicular magnetic field is given by

It is obvious that a nonzero Y-shaped Kekul´e texture breaks the valley degeneracy of all Landau levels except those of the zero mode. As we show in the next section,this leads to a new type of anomalous quantum Hall effect,which is distinct from that of pristine graphene.[19-21]

Fig.2. Landau level spectrums of Y-shaped Kekul´e-patterned graphene as a function of the perpendicular magnetic field for Kekul´e bond texture amplitudes of(a)Δ0=0.079 and(b)Δ0=0.200.

2.2. Hall and longitudinal conductivity

To proceed,one needs the product of the velocity matrix elements. After evaluating and inserting them into Eq.(8),we arrive at

wheregσ=2 is due to two-fold spin degeneracy (this is the case in which the Zeeman splitting is smaller than the Landau level broadening). After some cumbersome but straightforward calculations,the Hall conductivity can be written as

In a 2D electron system, a perpendicular magnetic field confines the electrons in quantized cyclotron orbitals. Therefore,at very low temperatures,the diffusive contribution to the conductivity vanishes and only its collisional(or hopping)part is nonzero.[33]The latter arises as a result of the migration of the cyclotron orbit due to electron-impurity scattering,which is assumed to play a key role in the transport properties of our system,as it is usual in other two-dimensional graphene-based materials.The longitudinal conductivity can therefore be written as[29,30,33]

whereniis the impurity concentration,Fζζ′(u)=〈ζ|eiq.r|ζ′〉is the form factor withu=l2q2/2=l2(q2x+q2y)/2,andU(q)is the Fourier transform of the impurity potential,which is taken to be that of the screened charges,U(r)=e2e-ksr/4πεrε0r,in whichksis the screening wave vector,εris the relative permittivity,andε0is the permittivity of vacuum. If the impurity potential is strongly short ranged, one may use the approximationks≫qand ignore theqdependence of the Fourier transform of the impurity potential. Since the scattering is elastic and the eigenvalues do not depend onkx, only the transitionsn →n′=nare allowed. Furthermore, we have(yζ-yζ′)2=l4q2cos2φ, whereφis the azimuthal angle in polar coordinates.Hence,transforming the sums into integrals

3. Results and discussion

In this section, using the analytical expressions obtained in the previous section, the effects of the Y-shaped Kekul´e bond texture on the transport coefficients of Kekul´e-patterned graphene are investigated. In our calculation, we use the valuest= 3 eV anda= 0.142 nm for the intra-layer hopping energy and the intra-layer carbon bond length of pristine graphene,respectively.

In Fig. 3, we plot the Hall and longitudinal conductivities of Y-shaped Kekul´e-patterned graphene as a function of the chemical potential for fixed values of the magnetic field ofB=7 T, a temperature ofT=5 K, and a Y-shaped Kekul´e bond texture ofΔ0= 0.2 (Fig. 3(b)), compared to those of pristine graphene (Fig. 3(a)). The other parameters areni=5×1013m-2,εr=4,andks=5×107nm-1.In order to make the effects of the Kekul´e bond texture more evident,we used a large value,Δ0=0.2,for it.[10]As is usual in the quantum Hall regime in two-dimensional materials,the Hall conductivity exhibits plateaus,and the transition regions between the plateaus of the Hall conductivity are accompanied by peaks in the longitudinal conductivity. Comparing Figs. 3(a) and 3(b) shows that in the presence of the Y-shaped Kekul´e bond texture,additional plateaus appear (at±ne2/hforn=2,4,6,...) in the Hall conductivity of the Kekul´e-patterned graphene, and that each peak of the longitudinal conductivity(except the peak located at a zero chemical potential)is split into two peaks.

The Hall plateaus displayed in Fig. 3 can be explained as follows. The Landau levels of pristine graphene are fourfold degenerate,so each Landau level contributes 4e2/hto its Hall conductivity. On the other hand, as shown in Section 2,the Y-shaped Kekul´e bond texture lifts the valley degeneracy of all Landau levels except that of the zero mode, which remains fourfold degenerate. So,each Landau level(except for the zero-energy level) contributes 2e2/h(4e2/h) to the Hall conductivity in Y-shaped Kekul´e-patterned graphene, leading to the emergence of a 4e2/h-step at the zero chemical potential and 2e2/h-steps at other points in Fig.3. Moreover,due to the lifting of the valley degeneracy by the Y-shaped Kekul´e bond distortion, each peak of the longitudinal conductivity (except the peak located at zero energy)is split into two peaks.

Fig.3. The Hall and longitudinal conductivities of(a)pristine graphene and(b)Y-shaped Kekul´e-patterned graphene for a Kekul´e distortion of Δ0=0.2 versus the chemical potential. The other parameters are B=7 T, T =5 K,ni=5×1013 m-2,εr=4,and ks=5×107 nm-1.

As shown above, Y-shaped Kekul´e-patterned graphene exhibits a new type of anomalous quantum Hall effect,which is distinct from that of pristine graphene.[19-21]The origin of the zero-energy Landau-level degeneracy and thus the anomalous quantum Hall effect in Kkeul´e-patterned graphene, as in pristine single and bilayer graphene,[19,35,36]can be explained using the Atiyah-Singer index theorem.[28]According to this theorem,the existence of zero-energy states in curved lattices with identical topologies(e.g.,for a corrugated graphene sheet with the same topology as that of a graphene lattice[37])and/or in presence of a gauge field (the usual electromagnetic field provides just the simplest example of these fields),is guaranteed, for topological reasons. This means, in particular, that the number of zero-energy states expressed in terms of the total pseudo-magnetic/magnetic flux per torus in the units of the flux quantum is a topological invariant.[36,37]The number of zero-energy states can also be determined by the dimensions of the zero-energy eigenspaces.[37,38]For Kekul´epatterned graphene,if we decompose[10]H=π+S++π-S-,withS±=vF(σx±iσy)⊗τ0+vFΔ0σ0⊗(τx±iτy)andσ0,σx,andσy(τ0,τx, andτy) act on the sublattice (valley) degree of freedom, we see that the full spaces of bothS+andSare composed of two irreducible rank-two null spaces,leading to a twofold degenerate zero mode forHand confirming the two-fold degeneracy of the zero-energy states. The degeneracy of the zero-energy states can be experimentally checked by measurements of the quantum Hall activation gaps of Kekul´epatterned graphene,similarly to Ref.[39]for the case of pristine single-layer graphene.

The Landau levels of pristine graphene, due to its linear band dispersion,are proportional to the square root of the indexes of the Landau levels. For this reason,the Landau levels close to the Dirac point are more widely spaced,allowing the quantum Hall effect (±2e2/hplateaus in the Hall conductivity) to be observed under very magnetic field, even at room

Fig.4. The Hall and longitudinal conductivities of Y-shaped Kekul´e-patterned graphene(lower panel)for amplitudes of(a)Δ0=0.079,(b)Δ0=0.097,(c)Δ0=0.126,and(d)Δ0=0.179 of the Kekul´e bond texture versus the chemical potential. The appearance of 4e2/h-steps is evident.

Figure 6 shows a Landau fan diagram[43-45]of(a)longitudinal conductivity and(b)Hall conductivity,in units ofe2/h,as a function of the magnetic field amplitude and the electron density. In Fig.6, as in a conventional quantum Hall system,the Landau fan diagram exhibits straight lines that converge to the origin, tracking maxima in the longitudinal conductivity(Fig. 6(a)) and demarcating plateaus in the Hall conductivity(Fig. 6(b)). A Wannier diagram[46]has shown that the slope of each line of the longitudinal conductivity is precisely the Landau level filling factor,ν. Moreover, one can see that the peaks of the longitudinal conductivity broaden with increasingB, which is due to the broadening of the density of states.[31]On the other hand, with decreasingB, one sees numerous superficial peaks (at low electron densities) that gradually disappear whenBvanishes. The reason for this is that for weak fields (B), the number of Landau levels near the Fermi level participating in the longitudinal conductivity increases.Another notable feature of the fan diagram is that the number of peaks (and also the plateau borders) doubles for finiteΔ0,due to the lifting of the valley degeneracy.[31,44,45]Finally,it is worth mentioning that since,in this paper,the calculations are limited to low-energy electron transport, the fractal effects of Hofstadter butterfly spectra cannot be observed.

Fig. 5. (a) Energy spectrum of Kekul´e-patterned graphene as a function of the magnetic field amplitude and the energy and (b) a counter plot of the quantized Hall conductivity of Kekul´e-patterned graphene as functions of the energy and the magnetic field amplitude, for Δ0 =0.200 and T =5 K.In (b), the quantized values of the Hall conductivity inside the energy gaps are indicated by numbers. The Hall conductivity has been determined in the white areas.

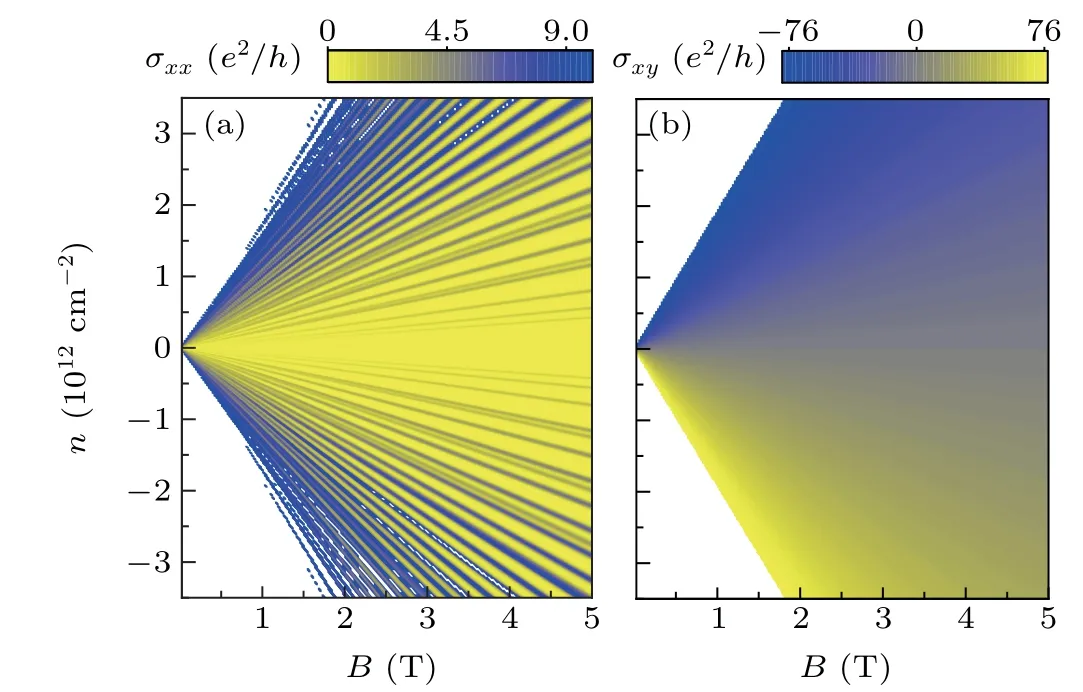
Fig. 6. Landau fan diagram of (a) longitudinal conductivity and (b) Hall conductivity, in units of e2/h, as a function of the magnetic field amplitude and the electron density. The Hall and longitudinal conductivities have been determined in the white areas.

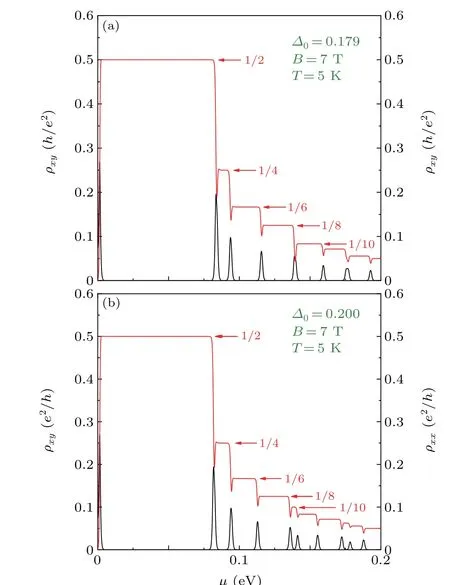
Fig.7. The Hall and longitudinal resistivities of Y-shaped Kekul´e-patterned graphene as a function of the charge carrier density for amplitudes of (a)Δ0=0.179 and(b)Δ0=0.200 of the Kekul´e bond texture. The other parameters are B=7 T,T =5 K,ni=5×1013 m-2,εr=4,and ks=5×107 nm-1.

4. Summary and conclusions

Acknowledgement

Project supported by the Farhangian University.