Topological properties of non-Hermitian Creutz ladders

Hui-Qiang Liang(梁辉强) and Linhu Li(李林虎)

Guangdong Provincial Key Laboratory of Quantum Metrology and Sensing&School of Physics and Astronomy,Sun Yat-Sen University(Zhuhai Campus),Zhuhai 519082,China

Keywords: topological phases,bulk-boundary correspondence,non-Hermitian physics,Creutz ladders

1. Introduction

Topological phases of matter are fascinating as they host robust in-gap boundary modes protected by the topological properties of bulk bands under the periodic boundary condition (PBC), known as the bulk-boundary correspondence(BBC).[1-3]In recent years, the scope of topological phases has been extended to non-Hermitian Hamiltonians,which are physically relevant as effective Hamiltonians of, for instance,open systems or wave systems with gain and loss.[4-12]In non-Hermitian systems,the conventional topological BBC is modified by the non-Hermitian skin effect(NHSE),where all eigenmodes accumulate at the boundaries due to non-Hermitian pumping.[13-19]The topological modes under the open boundary condition (OBC) are now topologically characterized by a non-Bloch Hamiltonian in the so-called generalized Brillouin zone,with the crystal momentum replaced by a complex value.[17-22]On the other hand, the NHSE itself also represents a unique topological phenomenon in non-Hermitian systems, originated in a nontrivial spectral winding of the complex spectrum.[23-26]

The Creutz ladder describes a one-dimensional(1D)twoleg ladder lattice with crosse-linked hoppings and a perpendicular magnetic flux.[27]Representing one of the minimal 1D topological insulating systems,the Creutz ladder and its variations have been employed to investigate various topological properties and phenomena,[28-37]such as topological quench dynamics,[28]effects of superconductivity pairing on fractionally charged midgap states,[29]cold atom realization of spinorbit coupling and quantum Hall insulators,[30]and competitions between topological features and interaction effects in quantum many-body systems,[34]among many others. Non-Hermitian extensions of the Creutz ladder or similar ladder models have also been introduced in investigating anomalous edge localization of eigenmodes (i.e., the NHSE),[13,14,38,39]non-Hermitian topological characterizations and BBC,[40-43]and a potential application of controlling the NHSE via lattice shaking.[44]

In many contemporary literatures,the Creutz ladder with on-site gain and loss is introduced as an equivalent of some simpler single-chain models with asymmetric hoppings,as the former is more experimentally feasible.[38-40]On the other hand,ladder models with asymmetric hoppings have also been considered in developing schemes for topological characterization of non-Hermitian Floquet systems.[42,43]In this paper, we provide a comprehensive investigation of the effects of these types of non-Hermticity acting on the Creutz ladder model,and unveil several remarkable behaviors of the system.We find that the NHSE is absent in some of the cases with asymmetric hoppings,as the induced non-reciprocities for different parts of the system are balanced and the system becomes reciprocal. Nevertheless,the topological characterization and transition are still distinct from that of Hermitian systems. In other cases with the presence of the NHSE,we unveil that the conventional BBC is not always violated in the presence of the NHSE and a nontrivial spectral winding. Furthermore,in our model, the NHSE induced by the imaginary on-site potential can be classified into two types, with the same and opposite skin localizations for the two bands,respectively,and the overall NHSE results from their competition. These scenarios with different non-Hermitian parameters are carefully examined in this work,and their topological transitions and phase diagrams are obtained analytically and/or numerically.

The rest of the paper is organized as follows.In Section 2,we set the stage of this paper by introducing the topological properties of the Creutz ladder model and the non-Hermitian parameters we considered. We then discuss the topological properties of our model in the absence and presence of the NHSE in Sections 3 and 4, respectively. Finally, our results are briefly summarized in Section 5.

2. Model Hamiltonian

Yet it belongs to the AIII class as the original Hamiltonian does not satisfy the time-reversal symmetry either for spinful or spinless systems. The model is thus topologically described by the winding of (hx,hz) throughout the Brillouin zone (BZ), and supports topologically distinguished phases with and without a pair of degenerate topological edge modes in the band gap[examples are shown Figs.1(a)and 1(b)]. Another parameter regime withθ=0,πyields a non-topological system as the Pauli matrixσzvanishes, and may only be gapped when|M|>|2r|.In more general cases,the non-trivial winding of (hx,hz) survives, but a nonzeroh0(k) induces ak-dependent shifting of the spectrum, which may lead to the overlapping of the two bands and the absence of a band gap in certain parameter regimes,as shown Fig.1(c).

Fig. 1. The Hermitian Creutz ladder model of Eq. (1) has three different topological phases, (a) a topologically non-trivial phase with a pair of degenerate in-gap edge modes, (b) a topologically trivial phase with a band gap, and (c) a gapless phase where the two bands overlaps. Blue and red colors indicate the two PBC bands, and gray dots are the OBC eigenenergies. The parameters are (a) M =0.25, r=0.5, θ =π/2, (b) M =0.75,r=0.25,θ =π/2,(c)M=0.75,r=0.25,θ =π/4,with L=30 unit cells.A sketch of the Creutz ladder model with all non-Hermitian parameters considered in this paper is shown in(d).

Compared with the SSH model, the Creutz ladder has more tunable parameters, and the existence of a nonzerokdependenth0term breaks the symmetry of the spectrum betweenEand-E. Thus richer phenomena may emerge when non-Hermiticity is introduced to different parameters of the Hamiltonian, as discussed in the following sections. Specifically, we shall focus on two types of non-Hermiticity widely investigated in literatures,namely,extra imaginary on-site potentials given by

withr1,2,m, andαtaking real values, and±corresponding to the hoppings toward opposite directions. Note that iαdoes not involve the±sign as it appears in the phase factor,which already takes opposite sites for hoppings toward different directions;and the parameterrdescribes two different inter-cell hoppings,hence the non-reciprocities can be added in two different ways(described byr1andr2, respectively), as demonstrated in Fig.1(d)together with all other parameters.

With these extra non-Hermitian terms introduced to the model, a key consequence is that certain non-reciprocities along the 1D ladder may be induced to the system,and some of which lead to the NHSE.Interestingly,the NHSE does not always alters the conventional bulk-boundary correspondence in our model. These results are briefly summarized in Table 1.Following the conclusion in Refs.[23,24],the existence of the NHSE has a correspondence to a nontrivial point-gap topology of the system,[46]described by a nonzero winding of the spectrum in its Brillouin zone. A system free from the NHSE shall generally have its eigenenergies moving along an arclike spectrum back and forth whenkvaries along the Brillouin zone,therefore its eigenenergiesE(k) are paired betweenkandk′,satisfying

withk/=k′for any given crystal momentumk(except for the end points of the arclike spectrum).[17-20]To give a clear demonstration,we shall use this criterion to analyze the NHSE and topological in-gap edgemodes for different non-Hermitian parameters separately.

Table 1. Summary of the non-reciprocities along x and the resulting properties of different non-Hermitian parameters. A longitudinal non-reciprocity corresponds to asymmetric hoppings along the 1D ladder, and a transverse one corresponds to that between the two sublattices.

3. Without the non-Hermitian skin effect

In this section we will discuss the cases without the NHSE,i.e.,with non-Hermiticity induced bym,r1,orα.

3.1. θ →θ+iα

We first consider the case with an imaginary phase factor,which leads to hoppings with asymmetric amplitudes given by e±αtoward right and left(left and right)for sublatticeA(B),respectively. The non-reciprocities of the two-sublattices are thus balanced and the NHSE is expected to be absent in this case. The Hamiltonian in momentum space is given by

which meansE±(k)=E±(-k)and the eigenmodes are paired between±k.

Now thathzcontains both sine and cosine ofθ,a nontrivial winding of (hx,hz)may exist even whenθ=0, yet it lies in the 2D plane of(the real part of)hxand the imaginary part ofhz. More generally, (hx,hz) can now be taken as a fourdimensional (4D) real vector (Re[hx],Im[hx],Re[hz],Im[hz]).Nevertheless, in our model the trajectory of this vector withkvarying from 0 to 2πalways lies in a 2D plane in the 4D space,ashxis real and the ratio of

where the system possesses a nontrivial winding of(hx,hz)in the plane shown in Fig. 2(a). That is, the topological phase transition is only associated withMandr, which is further confirmed by the transfer matrix approach in Appendix A.

Fig.2. (a)Sketches of the winding of(hx,hz)within a 2D plane in the 4D space of(Re[hx],Im[hx],Re[hz],Im[hz]),for the system described by Eq.(6).The axis of Im[hx] is omitted as hx takes real value in this system. (b)-(d)OBC spectra of the system under different parameters. Red stars represent a pair of degenerate eigenmodes localized at opposite ends of the 1D ladder with L=200. The parameters are θ =π/2,π/4,0 from(b)to(d),and M=1,2,2.5 from top to bottom. The middle row is at the topological transition point with M=2r. Other parameters are r=1 and α =2. Dash lines indicate line gaps in (b) and (c), and in (d) the spectrum only possesses a point-gap as it encloses a finite area.

Finally, we note that due to the non-Hermiticity, the eigenenergies now are distributed in a 2D complex plane,hence the definitions of energy gap and in-gap eigenmodes are also richer than that for Hermitian systems. In our model,the two bands are well-separated whenθ/=0 (orπ), and a linegap exists except for the topological transition point,as shown by the dash lines in Figs. 2(b) and 2(c). Such a line-gap is an analog of the energy gap of Hermitian systems, which is given by a line parallel to the imaginary axis in the context of non-Hermitian systems. In Fig. 2(d) withθ=0, the two bands always connect to each other,leading to the absence of a line-gap. Nevertheless,the spectrum is seen to have a pointgap, and a pair of degenerate edge eigenmodes appears to be separated from the bulk bands when|M|<|2r|,where(hx,hz)corresponds to a nontrivial winding.

3.2. M →M±m and r →r±r1

Next we consider the other two non-Hermitian terms ofmandr1which enter the Hamiltonian in similar manners. That is,they both induce even functions ofkto the third Pauli matrices (which isσyin the Creutz ladder model), and now the Hamiltonian matrix in the momentum space reads

Note that the NHSE is also expected to be absent in this scenario,as both of these two parameters do not induce a net nonreciprocity alongxdirection:mdescribes asymmetric hoppings between the two sublattices within the same unit cell,andr1induces opposite non-reciprocities for hoppings between sublattices(ax,bx+1)and sublattices(ax,bx-1). Indeed,this system is free from the NHSE,as it satisfies

taking a real value, the square root of which gives the energy difference between the two bands at eachk.

We first consider the simplest case withθ=±π/2,whereh0=0 and the two bands do not overlap. The system satisfies a non-Hermitian chiral symmetry[20,47]

and has four topologically different phases depending on the value ofP(k) and the existence of in-gap edgemmodes.[20]

The topologically distinguished phases can further be identified when a real line-gap exists,manifested by the existence or absence of in-gap edgemodes with the same real energy.

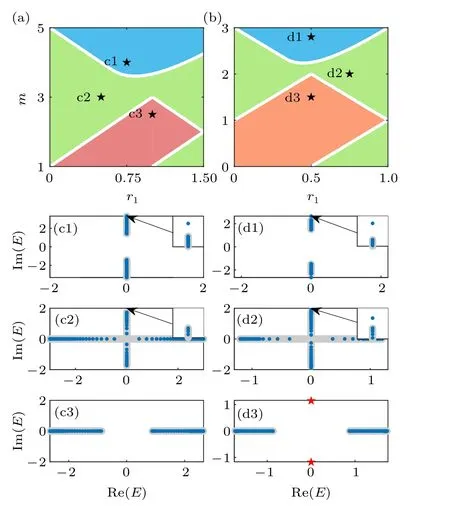
Fig.3. (a)and(b)Phase diagrams of the system described by Eq.(9),with(a)M=3,r=1,θ=π/2 and(b)M=r=1,θ=π/2.The white solid lines are obtained from conditions of Eqs.(14)-(16). (c)and(d)The PBC(gray)and OBC(blue dots and red stars)spectra at the black stars in(a)and(b),respectively,for a system with L=50 unit cells.The parameter are(c1)m=4,r1=0.75,(c2)m=3,r1=0.5,(c3)m=2.5,r1=1,(d1)m=2.8,r1=0.5,(d2) m=2, r1 =0.75, and (d3) m=1.5, r1 =0.5. Red stars in (d3) are edgemodes protected by a real line-gap. Insets in(c)and(d)show isolated edgemodes with zero real energies, which are not topologically protected due to the absence of a real ling-gap.

In Figs. 3(a) and 3(b) we illustrate the phase diagrams of our system withθ=π/2 in different parameter regimes,where the phase boundaries are given by Eqs. (14)-(16), as detailed discussed in Appendix B.Typical spectra for the different phases are shown in Fig. 3(c) and 3(d). Note that in the gapless and the imaginary-gapped phases, edgemodes may also appear apart from the PBC spectra, as shown in Figs. 3(c1), 3(d1), and 3(d2). Nevertheless, now these edgemodes,having nonzero imaginary energies only,can continuously merge into the bulk without changing the gapped or gapless nature of the spectrum,meaning that they are not topologically protected. On the other hand, similar edgemodes with zero real energy also appear in Fig.3(d3),where they are topologically protected by the real line-gap.[20]

For more general cases withθ/=±π/2, a nonzero but realh0shifts the real part of the eigenenergies with the same amount for eachk. Thus another gapless phase with Re[E±]overlap each other may emerges whenθis tuned away from±π/2, as illustrated in Fig. 4. The overlapping condition is given by

and the corresponding phase transition point can be determined accordingly, as shown in Fig. 4(a) atθ ≈0.22π, and in Fig. 4(c) atθ ≈0.28π. On the other hand, tuningθalso affectsP(k) throughhz=-2sinksinθ, and can lead to another transition to the gapless phase, satisfying the condition of Eq.(16). Such a phase transition is shown in Figs.4(c)and 4(d)atθ ≈0.20π.The critical values of these transition points are also obtained analytically(see Appendix B).

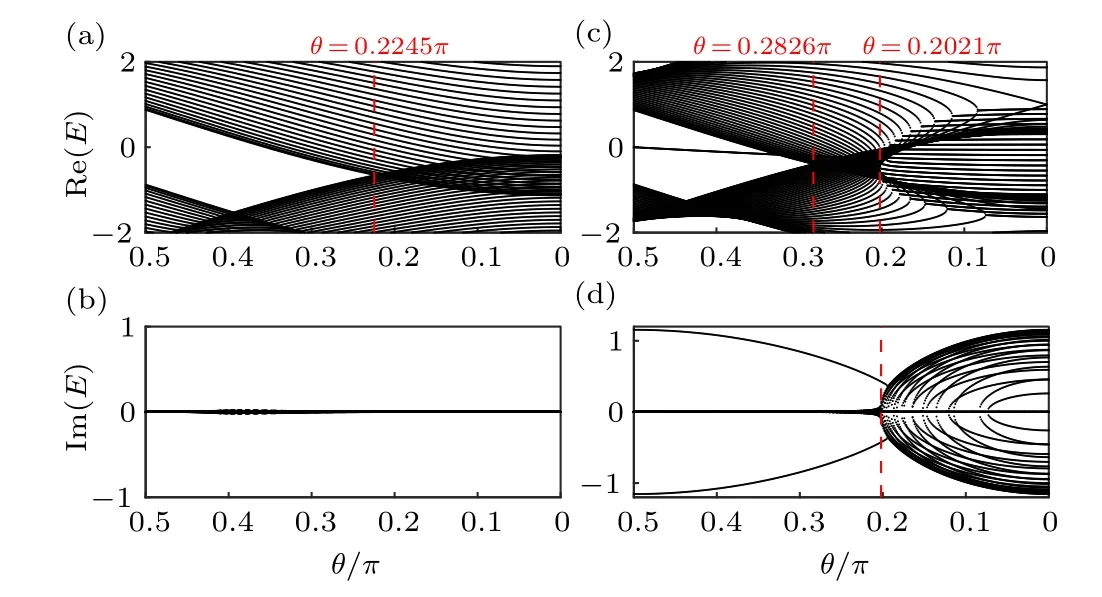
Fig.4.OBC spectra of the system described by Eq.(9),with θ varying from π/2 to 0. The parameters are M=3,r=1,m=2.5,r1=1 for(a)and(b),the same as that of Fig.3(c3);and M=r=1,m=1.5,r1=0.5 for(c)and(d),the same as that of Fig.3(d3). The red dash line in(a)and the first one in(c)are obtained from the condition of Eq.(17),describing the transition from a real-gapped phase to a band-overlapping gapless phase. Those at θ ≈0.2021π in (c) and (d) are obtained from the conditions of Eqs. (14)-(16),describing the transition to a band-touching gapless phase,where some eigenenergies of the bulk eigenmodes acquire imaginary values.

4. With the non-Hermitian skin effect

In contrast to the scenarios discussed above, the other two non-Hermitian parametersr2andµlead to certain nonreciprocities along the 1D ladder,as elaborated below.

4.1. r →r±r2

In the presence of a non-zeror2, the Bloch Hamiltonian is given by

withw(Er)for a reference energyErenclosed by the spectral loop. The full spectrum of the system forms two loops in the complex plane,and gives a spectral winding numberν(Er)=2 forErenclosed by both loops,as shown in Fig.5(a). Yet this high winding is relatively trivial as it is merely a sum of the winding numbers of two independent systems. On the other hand,withθtuned away from 0 andπ,a nonzerohzemerges and couples the two sub-chains. The two spectral loops ofσx=±1 are thus restructured into two bands, which can inherit the spectral windings of both decoupled sub-chains in certain parameter regimes [see Figs. 5(a)-5(c)]. As a result,the high spectral winding is now an intrinsic property of a single band,even though the overall system possesses only nearest neighbor hoppings.

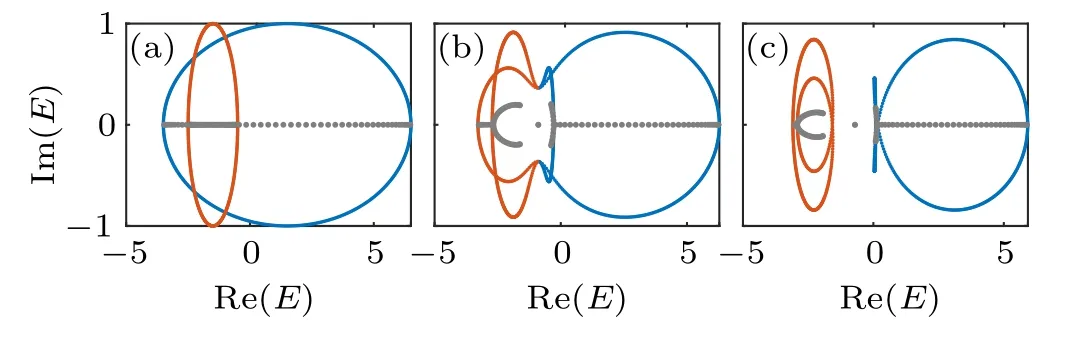
Fig. 5. The PBC (red and blue) and OBC (gray) spectra, with (a) θ =0,(b) θ =0.15π, and (c) θ =0.25π. In panel (a), red and blue colors indicate the PBC spectra corresponding to the two decoupled sub-chains with σx =±1, respectively. In (b) and (c), these two components are coupled,and the colors are marked regarding E+(k) (blue) and E-(k) (red) with Re[E+(k)]>Re[E-(k)]. A winding number ν(Er)=2 can be obtained for a reference energy Er enclosed by both loops in(a),or enclosed by the red one twice in(c). Other parameters are M=r=1.5 and r2=0.5.

Despite the existence of a nontrivial spectral winding and the NHSE,the conventional BBC is not always violated in this system. To see this, we first write down the eigenenergies of the system under PBC,given by

When|r2|<|sinθ|, the PBC spectrum is seen to form two separated loops(e.g.,as in Fig.5(c)),and the line-gap between them may close only at a DP satisfying the above condition(i). In such a scenario,the topological phase transition under the OBC is also seen to occur at the DP withM=±2r,as shown in Figs.6(a)and 6(b). This observation suggests that the conventional BBC still holds in this parameter regime.The reason is that the spectral winding topology requires the OBC arc-like spectrum to fall within the PBC loop-like one,[23,24]so that the gap-closing conditions for them may be different from each other only after the system goes through an exceptional PBC gap-closing,as further explained in Appendix C.

With the amplitude ofr2increasing, two EPs satisfy the above condition(ii)when|r2|=|sinθ|,and the two loops connect each other and reform two overlapping loops(e.g., as in Figs.5(a)and 5(b)). As now a line-gap is absent for the PBC spectrum, the two OBC bands may go through a gap-closing in the interior of the PBC loops, without generating either a DP or an EP to the PBC spectrum(see Appendix C).

In Fig. 7(a) we illustrate a phase diagram of the system,where four different phases are seen from our numerical results [Figs. 7(b)-7(e)]: two topologically nontrivial phases with in-gap edge modes[Figs.7(b)and 7(e)],a trivial gapped phase[Fig.7(d)],and a gapless phase[Fig.7(c)].It is seen that when|r2|>|sinθ|, the phase boundaries, including that between two topologically different gapped phases in Figs.7(b)and 7(e), cannot be predicted by the PBC gap closing (white solid lines).

Note that the dash lines in Fig.7(a)are read out by comparing the spacing between different eigenenergies from the numerical results of the energy spectrum[e.g.,as in Figs.6(c)and 6(d)]. These boundaries may not be the accurate ones,as topological properties of a non-Hermitian system can also depend on the system’s size,[49]and numerical results of non-Hermitian Hamiltonians suffer from strong computational error for large systems.[22]Furthermore,the criterion for identifying a gap also become blurred, especially when the system is near the phase boundaries, as now the eigenenergies take complex values.

Fig. 7. (a) A phase diagram of the system described by Eq. (18), with r =1.5, θ =π/4, and L=40. The white solid lines are obtained from the conditions of Eqs. (23) and (24), and the white dash lines are obtained numerically. The two black dash lines represent the parameter regions for the numerical results in Figs. 6(a), 6(b) and 6(c), 6(d), respectively. (b)-(d)OBC spectra corresponding to the four black stars in(a),with(b)M=1,r2 =0.5; (c) M=1, r2 =1.5; (d) M=1, r2 =2; and (e) M=3, r2 =2.Red stars are the topological in-gap eigenmodes.

4.2. Imaginary on-site potentials

Last but not least, we consider the case with sublatticedependent imaginary on-site potential termHµadding to the Hamiltonian,

Nonzeroµa,brepresent unbalance on-site dissipations on the two sublattices, which may also induce the NHSE under certain circumstances.[38,44,50]Here we further chooseµb=-µa=µ, as any other choice is equivalent to it upon a uniform shifting of the spectrum along the imaginary axis. The overall Bloch Hamiltonian with the on-site dissipations now reads

Unlike the non-Hermiticity discussed in previous sections, the imaginary on-site potentialµdoes not directly induce non-reciprocity (i.e., asymmetric hoppings) to the system. Yet with the rotation of the pseudospin in Eq. (3), the parametersMandµform asymmetric intra-cell hoppings as in the non-Hermitian SSH model,and induce nontrivial spectral winding and the NHSE to the system. In other words, a nonzeroµinduces a “hidden” non-reicprocity to the Creutz ladder, and leads to the NHSE. Consequently, conventional topological properties associated with in-gap edge modes shall also be affected by the NHSE.[17]In the following of this section we shall first give an analysis of the NHSE in this model,then discuss its topological in-gap edge modes.

4.2.1. Competition between two types of NHSE

To analyze the NHSE in this model,we shall first consider two special parameter regimes. The first one is withθ=π/2 andr=sinθ=1. Under such conditions, the Hamiltonian can be exactly mapped to the well-studied non-Hermitian SSH model,[17,19,51]withM±µand 2r=2 being the strengths of the non-reciprocal intracell and reciprocal intercell hoppings.Thus a uniform NHSE emerges with the inverse localization length of all the skin modes given by[17]

i.e.,eigenmodes of both bands have the same distribution[see Fig.8(a)]. With the chosen parameters, the PBC spectrum ofh(k) forms two loops for the two bands, leading to nonzero spectral winding numbers

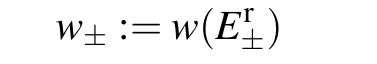
whereEu,±(k+iκu)are the eigenenergies of the Hamiltonian of Eq.(26)in the GBZ,withθ=π/2 andr=1.

Fig.8. The PBC(red and blue)and OBC(gray)spectra,and the summed population ρ±(x)=∑n∈±[|ψAx,n|2+|ψBx,n|2]for each of the the two bands,where ψβx,n is the amplitude of the nth eigenmode on β sublattice of the xth unit cell, and the summation runs over all the eigenmodes of one of the two bands (“+” for the band marked blue and “-” for that marked red). The spectral winding numbers w± defined for the chosen reference energies Er± (black stars)are indicated in the figures. Note that the maximum value of ρ-(x)in(c)is ～1.5,and that of the rest is ～10(no shown in the figure). The parameters are r=1,µ =0.5,L=30,with(a)M=1.35,θ =π/2,(b)M=0,θ =π/4,and(c)M=1.35,θ =π/4.

Next we consider another parameter regime withM=0.The inverse localization length defined in Eq. (27) becomesκu=0,meaning the absence of the uniform NHSE.However,the PBC spectrum remains as loops, and the OBC system is seen to exhibit a bidirectional NHSE,namely,the eigenmodes of the two bands accumulate to opposite ends of the 1D ladder,as shown in Fig.8(b). The spectral winding numbers also satisfyw+=-w-for the reference energies enclosed by different bands. The corresponding inverse localization lengthκbis found to bek-dependent from our numerical computation(results not shown),and is difficult to obtain analytically.Nevertheless,it is straightforward to see that the eigenenergies in this parameter regime satisfy

The exact relation betweenkandk′is unknown, yet from Eq.(28)we will also have

i.e.,the eigenmodes associated withkandk+πhave opposite inverse localization lengths for the two bands, thus they shall accumulate at different ends of the system under the OBC.

Now that we have two types of NHSE, the competition between them is expected in a more general parameter regime.Following previous discussion, the two types of NHSE shall induce opposite localizing directions to only one of the two bands, which is the one labeled with “-” for the parameters we chosen in Fig.8(c). Specifically,when the absolute values of their inverse localization lengths are approximately equivalent, the“-”band shall have almost identical PBC and OBC spectra, with its eigenmodes experiencing only a very weak skin localization, as shown in Fig. 8(c). It also indicates that the total inverse localization lengthκ(k), with contributions from bothκuandκb(k),is not onlyk-dependent,but also takes different values for different bands.

To describe the competition between the two types of NHSE and give a phase diagram regarding which of them dominates in the system, we define a directed inverse participation ratio(dIPR)as

which describe the average localizations and their directions of the two band labeled by “±”. Here the summation runs over all eigenmodes belonging to the corresponding energy band,N=L-1 when the system hosts in-gap topological edge modes, andN=Lwhen it has not. We can see from Figs.9(a)and 9(b)that the two bands localize toward different directions in different parameter regimes. Finally,in Fig.9(c),we illustrate the value ofI ≡¯Id,+× ¯Id,-, which takes positive value when the two bands share the same direction of the skin localization,i.e.,the system is dominated by the uniform NHSE(the red region);and negative value when the two bands mostly localize at different ends of the system,i.e.,the system is dominated by the bidirectional NHSE(the blue region).

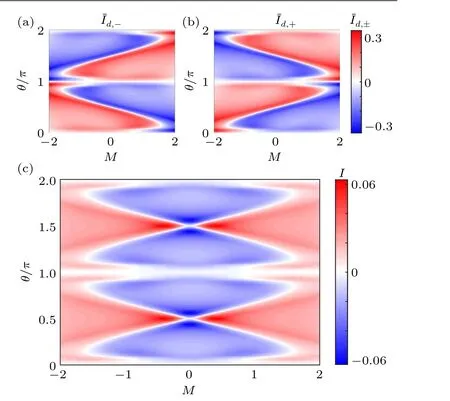
Fig. 9. (a) and (b) The average ¯Id,± dIPR defined in Eq. (30) for the two bands,respectively,versus the parameters θ and M. (c) The product of ¯Id,+and ¯Id,-,within the same parameter regime as that of(a) and(b). Positive(negative)I indicates that the system is dominated by the uniform(bidirection) NHSE, namely, the two bands tend to localize at the same (opposite)ends of the 1D ladder. Other parameters are r=1,µ =0.5,and L=30.

4.2.2. Topological edge modes

Next we shall consider the topological in-gap edge modes and associated topological phase transitions in this model. As in the previous subsection, we begin with the simplest case with

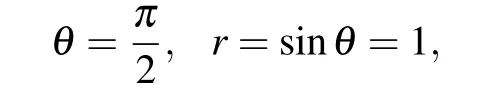
where the system is an analog of the non-Hermitian SSH model and is analytically solvable.[17]Following non-Bloch band theory, the OBC topological properties of this system are described by the non-Bloch Hamiltonianh(k+iκu), withκugiven by Eq. (27) which describes the locality of the skin modes under OBC.The system is topologically nontrivial with a pair of in-gap topological edgemodes when[17]

and we can obtain the phase diagram in Fig.12(a). The other panels in this figure illustrate typical OBC spectra of the three different phases,including a topologically nontrivial phase in Fig. 12(c), and two topologically trivial phases with real and imaginary line-gaps in Figs.12(b)and 12(d),respectively.

Whenθdiverges from±π/2,a nonzeroh0term emerges and leads to more complicated phase transitions in the system. For instance,in Hermitian systems,theh0term may induce an extra gapless phase with the two bands overlapping with each other, as shown in Fig. 1(c). However, it does not change the topology of each “band”, which is given by the eigenenergies continuously changed with the momentumk. In non-Hermitian systems, ash0only shifts the two PBC bands simultaneously and does not induce any degeneracies(normal or exceptional)between them,it is also expected to not change the BBC,either a conventional one,or a non-Bloch one raised from some other terms as in the current case.That is,the topological properties shall be described solely by the Hamiltonian matrixhσ(k):=h(k)-h0,which is still an analog of the non-Hermitian SSH model by setting

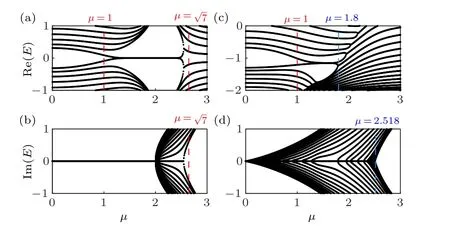
Fig. 11. The energy spectrum of h0 /=0 (top) and h0 =0 (bottom). For this condition h0 =0, the red and blue dash line is the topological phase transition point,µ =1,andµ =). For condition h0 /=0, the topological phase transition point and the point of imaginary spectrum starting to separate are indicated by red dash line and blue dash line,respectively. The parameters are system size L=30,θ =π/3,M=2.

By further comparing the spacing between different eigenenergies, we numerically obtain the phase boundaries between the four different phases, including the three withθ=π/2 in Fig.10,and an extra gapless phase due to the presence ofh0,as shown in Fig.12.It is seen that the phase boundary(white dash lines)between the two topologically different phases with a real line-gap [Figs. 12(d) and 12(e)] coincides with the topological phase boundary given by Eq.(32)(purple lines),which further confirms that the non-Bloch BBC associated withκuis not further modified byh0. On the other hand,in the region close toθ=π/2 andµ=3,the system goes into the regime with an imaginary line-gap before approaching the analytically predicted topological phase transition, which we believe is due to the finite size effect,as discussed above.

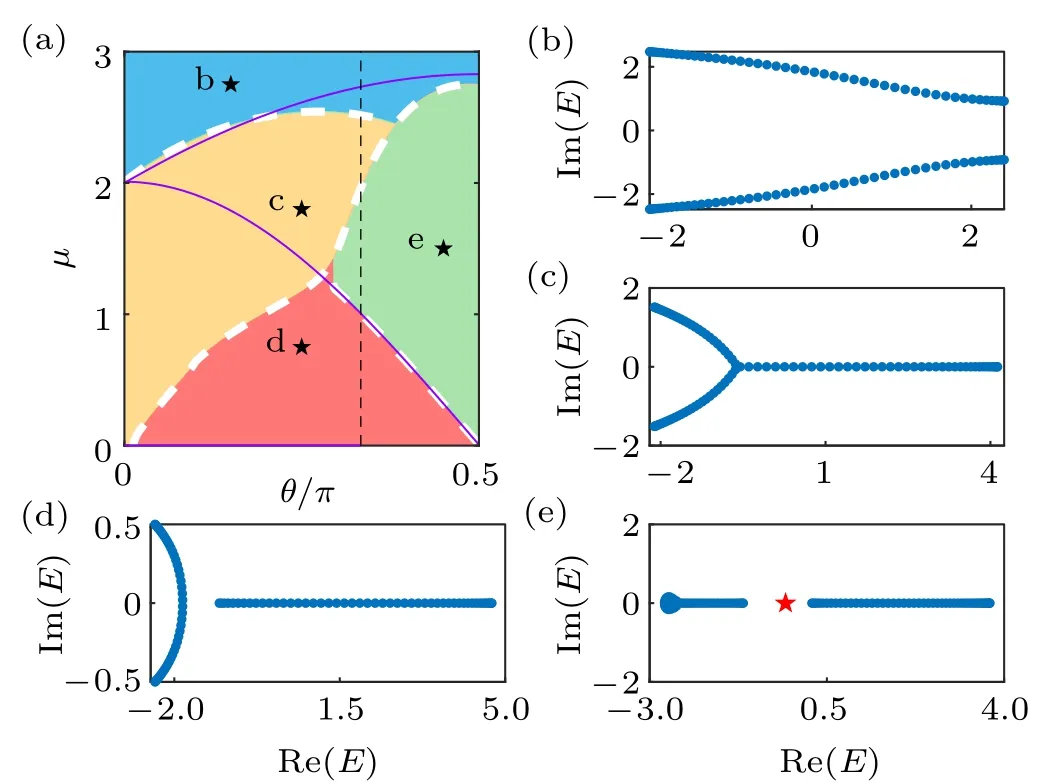
Fig. 12. (a) A phase diagram of the system described by Eq. (26), with r=sinθ, M =2, and L=50. The phase boundaries (white dashed lines)are obtained numerically, and the two purple lines are given by Eq. (32).(b)-(e) The OBC spectra corresponding to the four black stars in (a), with(b)θ =0.15π, µ =2.75;(c)θ =0.25π, µ =1.8;(d)θ =0.25, µ =0.75;and(e)θ =0.45,µ=1.5. Red stars are the topological in-gap eigenmodes.

Finally,we note that in a more general parameter regime withr/= sinθ, the non-Bloch Hamiltonian becomes more complicated as now the SSH analog no longer holds, and an analytical solution of the topological phase transition is difficult to obtain even omitting the effect ofh0. Nevertheless,compared with the previous cases,numerically we do not find any qualitatively different topological property in this general scenario.

5. Summary

In summary, we have comprehensively investigated the topological properties of a non-Hermitian Creutz ladder model with non-Hermiticity added in several different manners, including asymmetric amplitudes of each hopping parameter and on-site imaginary potentials. Besides carefully analyzing the topological phase transitions between gapped and gapless phases in each scenario, we further unveil that various phenomena can emerge depending on how the non-Hermiticity enters the Hamiltonian,including a winding topology in a 2D plane associated with a complex Hamiltonian vector,the emergence of a high spectral winding number without introducing long-range hoppings,and a competition between two types of NHSE. Additionally, we find that the NHSE does not necessarily lead to the breakdown the conventional BBC, which is also associated with whether EPs emerge in the concerned parameter regime.

Acknowledgement

The work is supported by the Guangdong Basic and Applied Basic Research Foundation, China(No.2020A1515110773).

Appendix A: Transfer matrix approach for the case with α

As discussed in the main text,the system with a nonzeroαis free of the NHSE,thus the topological edge modes under the OBC shall be directly associated with the a phase winding of eigenmodes of the Bloch Hamiltonianh(k) in Eq. (6).Here we first omit theh0(k) term as it does not affect the eigenmodes ofh(k). The possible topological edge modes are now fixed at zero-energy, as the resulting Hamiltonianh′(k)=h(k)-h0(k)satisfies a sublattice symmetry

Fig. A1. (a) and (b) The absolute values of λ1,2, the two eigenvalues of the transfer matrix TA, respectively. The gray translucent plane represents|λ1,2|=1. (c)A phase diagram of the system,determined by the numerical results of |λ1,2|. The yellow region with |λ1,2|<1 (|λ1,2|>1) means that an zero-energy eigen-solution localizing at the x=1 (x=L) exists for the A component, and another one localizing at x=L (x=1) exists for the B component. The blue region with |λ1|<1 and |λ2|>2 corresponds to no zero-energy eigen-solution. Note that due to the rotation of the pseudospin,here A and B are different combinations of the two sublattices of the Creutz ladder. Specially,|λ1,2|=1 along the dash lines at θ =0(2π)and π. Other parameters are α =2 and r=1.

Appendix B: Deriving the phase boundaries of the case with nonzeromandr1

Following the discussion in the main text, the model with non-Hermiticity given bymandr1exhibits no NHSE,and its phase transitions can be determined solely from the PBC Hamiltonian matrixh(k).Specifically,the band-touching point is given byP(k)=0,with

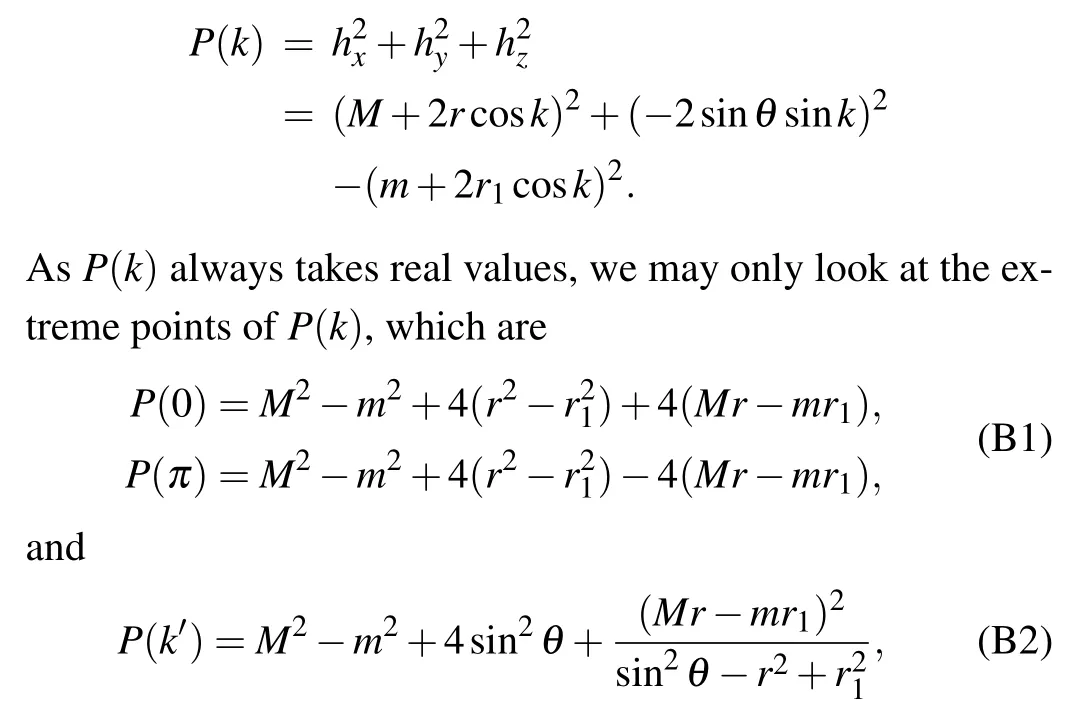
which are the same for this model as the conditions of Eqs.(14)and(15)in the main text. Otherwise,P(k)=0 must be satisfied for certain values ofk, as theP(k)takes different signs at different extreme points. In such a circumstance, the eigenenergies distribute along both the imaginary and real axes in the complex plane,and form a gapless cross-shape spectrum[see Figs.3(c2)and 3(d2)for some examples].

The phase diagrams in Fig.3 are obtained from the above conditions with the given parameters. That is, for the parametersM=3,r=1,sinθ=1 as that of Fig.3(a),the possible phase boundaries are given by

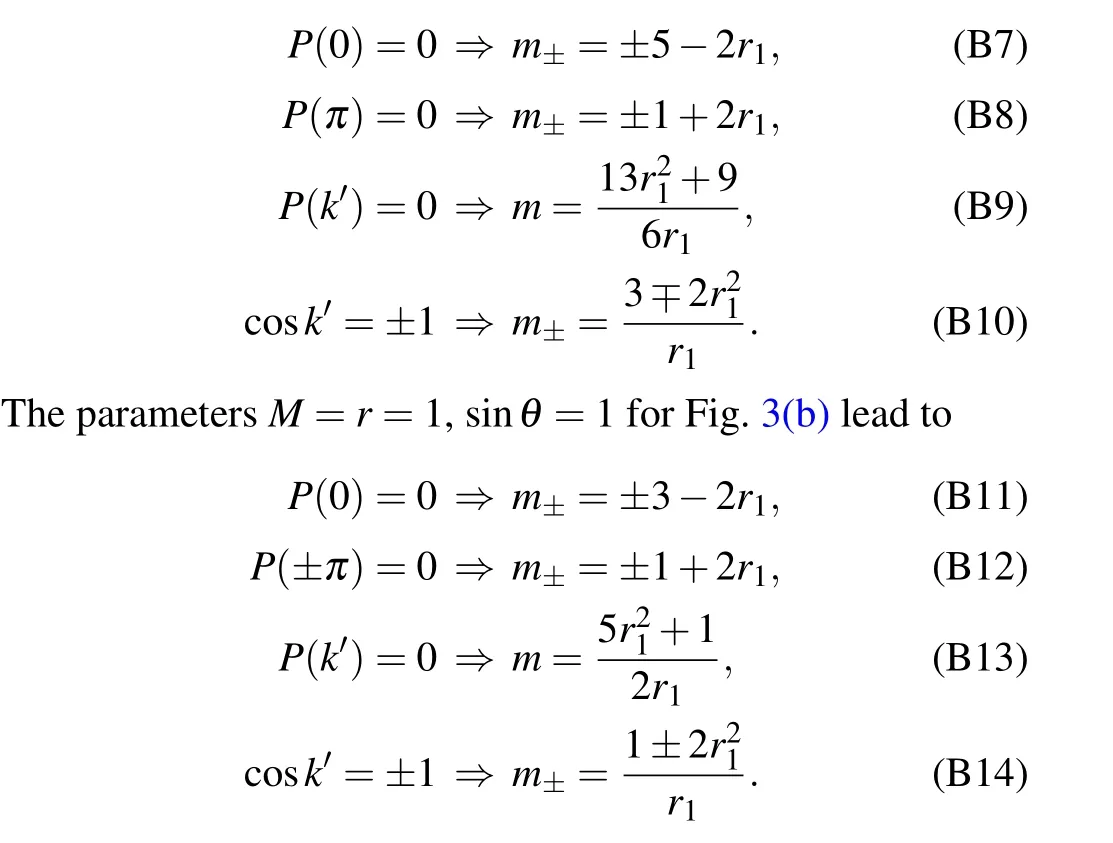
The lines and curves corresponding to these conditions are shown in Figs. B1(a) and B1(b), respectively, and the phase diagrams are obtained by further checking whetherP(k)takes positive or negative values within different areas separated by these lines and curves.

For a more general parameter regime withθ/=π/2,h0becomes nonzero and may lead to another gapless phase with the two bands overlap at differentkvalues. Here we shall consider the phase transition induced byθfor the two specific cases in Fig.4 as illustrations. The first one of Figs.4(a)and 4(c)is with the parameters

predicting a phase transition atθ ≈±0.2826π[see Fig. 4(c)in the main text]. Furthermore, now thatP(k) takes negative values for certain values ofkandθ,the system also supports a band-touching gapless phase in this parameter regime. The band-touching condition requiresP(k′)<0,asP(0)=2.75>0,P(π)=0.75>0 at the other two extreme points ofP(k).Therefore we obtain

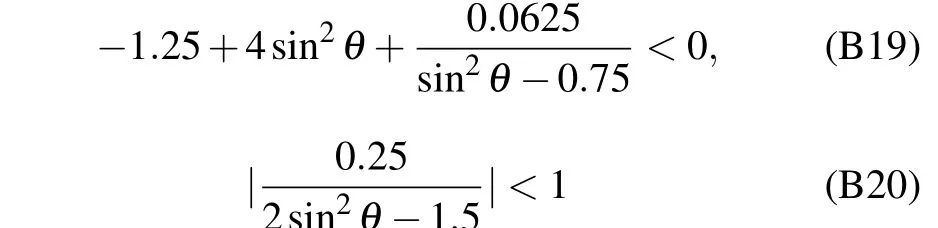
from Eqs. (B2) and (B4), respectively. Combining these two conditions, we reach the conclusion that the two bands touch and some eigenenergies acquire nonzero imaginary values when|sinθ|<0.59307, resulting in a transition point atθ ≈0.2021π[see Figs.4(c)and 4(d)in the main text].

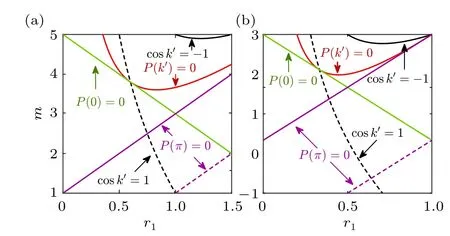
Fig.B1. Results from the conditions of Eqs.(B10)and(B14),with(a)M=3,r=1,θ =π/2 and(b)M=r=1,θ =π/2,the same as the parameters for panels(a)and(b)of Fig.3,respectively.

Appendix C: Conditions for preserving the conventional BBC in the presence of the NHSE

In this section we shall discuss the conditions for preserving the conventional BBC even in the presence of the NHSE.Specially, in order to violate the conventional BBC, the system must support exceptional points (EPs) between different bands at certain parameters. To see this, we first review the conditions for having the NHSE, and how the conventional BBC may be violated in non-Hermitian systems.

(i) For a non-Hermitian system, the NHSE has a correspondence to a loop-like PBC spectrum enclosing a nonzero area in the complex plane, and its OBC spectrum must lie within this area enclosed by the PBC spectrum,[19,21,23,24]as shown by the sketches in Fig.C1.

(ii)In a two-band non-Hermitian system with the NHSE,the two bands may connect into a big loop in certain parameter regimes,say for a parametertranging fromt1tot2,as shown by Figs.C1(c)-C1(e).

(iii)Its OBC spectrum is generally still given by two separated bands, yet the gap between them may close at certaintc∈(t1,t2), corresponding to the topological phase transition under OBC (Fig. C1(d)). However, the PBC spectrum has a band touching point only att=t1ort=t2,and shows no transition att=tc.Therefore the OBC topological phase transition attccannot be predicted by the Bloch Hamiltonian of the PBC system,which is known as the breakdown of the conventional BBC.

Fig.C1. Sketches for topological transition of the PBC(blue and red for the two bands)and OBC(gray)spectra when the conventional BBC is broken.t represents a parameter which drives the system to undergo a topological transition. The two PBC bands are assumed to touch each other at(b)t=t1 and(f)t=t2,and connect into a big loop(but without any degeneracy at any individual crystal momentum)for t1

Because of (i), a key condition for violating the conventional BBC is that the spectrum supports only point-gaps,but no a line-gap between the two concerned energy bands. In the above scenario, this condition is to have the two bands connecting into a single loop,where an adiabatic following of the eigenstates goes back to the initial state only after the momentumkvaries two periods, e.g., from 0 to 4π.[15]Such a scenario will give an overall Berry phase ofγ=πfor the two bands, meaning that the trajectory of the Hamiltonian vector must cycle an EP.[20,51,53,54]On the other hand, no EP is enclosed by this trajectory when the two PBC bands are separated,as the summed Berry phase of them must beγ=0. This is also always the case for Hermitian gapped systems. Therefore, when turning on certain non-Hermitian parameters, the conventional BBC may be violated only when the system goes into the former regime withγ=π, meaning that the system must goes through an exceptional gap-closing at some point,so that the trajectory of the Hamiltonian vector can enclose an EP.

Finally,we note that it is also possible to have a spectrum with only point-gaps by having the two energy bands overlapping with each other at different values ofk. This condition requires no any type of degeneracies between the two bands.However, we do not find such an example with the conventional BBC being violated.