Explosive synchronization in a mobile network in the presence of a positive feedback mechanism

Dong-Jie Qian(钱冬杰)

Jiangsu Provincial Sensor Network Engineering Technology Research Center,Wuxi Institute of Technology,Wuxi 214121,China

Keywords: complex network,explosive synchronization,positive feedback,mobile agent

1. Introduction

Synchronization is a collective phenomenon of a population of dynamically interacting units.Synchronization processes can be observed in many fields, such as biology,[1,2]neuroscience,[3,4]engineering,[5,6]or even in social sciences.[7]In the past, the Kuramoto model has been widely used in the study of synchronization[8-11]because it captures the essence of collective dynamics. The continuous and second-order phase transition from the incoherent state to the synchronous state has been widely studied using the standard Kuramoto model and its generalized forms.[12-15]However, phase transition is first order, abrupt and irreversible under certain conditions.[9,16-20]Jesus Gomez-Gardeneset al.[21]discovered this phenomenon firstly in heterogeneous networks by setting the natural frequency of the oscillator to be positively correlated with its degree. They named it explosive synchronization(ES)by referring to explosive percolation. Explosive synchronization has rapidly become a hot topic in the research frontiers of complex systems. Many mechanisms have been found to induce explosive synchronization transition, including frequency-weight,[16,22,23]time delay,[20,24]inertia,[25]and so on.[9,18,19,26,27]

Recently, positive feedback mechanisms that induce explosive synchronization have attracted increasing attention.Zhanget al.[17]utilized the local-order parameter to adjust the actual coupling strength of each oscillator. Using this method,they reported the explosive synchronization transition both in a single network and a multiplex network. Daiet al.[28,29]introduced a positive feedback mechanism between the coupling and the global-order parameter in theD-dimensional Kuramoto model and showed that the synchronization transition is explosive in all even dimensions, while it is mediated by a time-dependent rhythmic state in all odd dimensions.[30]Their studies provide inspiration for the understanding of the mechanism between the coupling of the elementary constituents and the level of coherence in the system. For example,if two neurons or neuronal systems are always excited at the same time,a“combination”will be formed. The excitation of one neuron will promote the excitation of the other.[31]

In this work, I study the synchronization phenomenon within the framework of a dynamic network. Although the synchronization of moving oscillators has been studied recently,[12,32-35]previous studies mostly explored the role of mobile networks in promoting synchronization. The method involving using the average property (global-order parameter in our work) of the whole system to adjust a single oscillator is rarely used in mobile networks.[36]In this paper, I first propose a Kuramoto model within the framework of dynamic networks, in which the coupling strength of the oscillator is controlled by positive feedback of the global-order parameters of the whole system. In addition, I study the influence of the symmetry of node frequency distribution on the synchronization phenomenon within the framework of a mobile network,and also discuss the impact of the communication radius on the phase transition mode. In Section 2, I propose the Kuramoto model in the presence of a positive feedback mechanism. In Section 3, numerical simulations are provided to explore the impact of parameters. Finally,I present a discussion and conclusions in Section 4.

2. Model

TheNKuramoto oscillators move in anL×Lsquare area with the periodic boundary conditions.And each oscillator has its phaseθi(i=1,2,...,N, θi ∈[-π,π]). The time evolution of the phase of the oscillatoriis defined as

whereωiis the natural frequency of the oscillatori,λis the overall coupling strength,andAi jare the elements of the adjacency matrixA;Ai j=1 if thei-th andj-th nodes are coupled,otherwiseAij=0. Hence,the degree of oscillators can be calculated andki=∑Nj=0Ai j. In our study, natural frequency is independent of the degree of the node.

Compared with previous studies,[32,33]our contribution lies in the coupling strength being tuned by the global-order parameterRthroughαi.Ris used to measure the coherence of the collective motion and can be defined byReIΨ=(1/N)∑Nj=1eIθ j, where 0≤R ≤1. The system is in an incoherent state whenR=0. The value ofRincreases gradually while the oscillators perform synchronization.Finally,the system is fully synchronized when the value ofRreaches 1.Here,Ψrepresents the average phase of all oscillators and I is the imaginary unit. I divide the oscillator in the system into two parts:one isffraction controlled oscillators,the other is 1-ffraction uncontrolled oscillators. In the controlled oscillators,αi=R,andαi=1 in the others. I make the global-order parameter positive feedback act on the coupling strength of the oscillators. In contrast to previous research,[17,37]I apply the global-order parameter of the whole system to each oscillator uniformly and positively. By utilizing this positive feedback control method,it is difficult for the system to generate a synchronized core in the network. Therefore, it is difficult for local synchronous communities to appear.

I use the dynamic network to describe the coupling relationship between oscillators. In anL×Lsquare area, each moving agent denotes an oscillator. In the initial state, all agents are randomly distributed in the area and move with angleφi(t)and velocityvi(t). Here,φi(t)(φi(t)∈[-π,π])denotes the direction of the movement of oscillatoriat timet,whilevi(t)denotes the speed of movement. Thus,the position of agentievolves in time as

wherexi(t)andyi(t)denote the horizontal ordinate and vertical ordinate of nodeiat timet,respectively. Andψi(t)is the change in the angle between timetandt+1. To meet the reality,I use Euclidean distance to judge whether the oscillators are coupled or not. Euclidean distance is defined as Only whenDij(t)≤r, the oscillatoriandjcan be coupled and perform synchronization at discrete timet,namely,Aij=1 whenDij(t)≤rotherwiseAij=0. Here,ris the communication radius. In wireless sensor networks, the communication radius refers to the wireless transmission and reception distance of each agent.[36]In our study,raffects the number of coupled neighbors of the oscillator. For the sake of simplicity,I set the communication radiusrof all nodes to be the same without additional explanation.

3. Simulation results

The numerical simulation results refer to a network ofNKuramoto oscillators. Without affecting the conclusion and properties of the simulation, I setN=500 for all plots. Initially,phaseθi(t)of all oscillators and the natural frequencyωiare drawn from a uniform probability distribution in[-π,π],unless otherwise specified. To calculate the phaseθi(t)of oscillatoriin Eq. (1), I solve the differential equations using the 4th-Runge-Kutta method with the integration time step dh=0.01. In addition, to compute a stationary value of the order parameter,the system is allowed to integrate for a longenough time period (105time step). To observe and track the phase transition, I change the coupling strength, which includes adiabatically increasing from the minimum value to the maximum value, and then adiabatically decreasing from the maximum value to the minimum value in small steps ofδλ. Furthermore, I take the steady value of the phase obtained from the last calculation as the initial state for the next iteration.

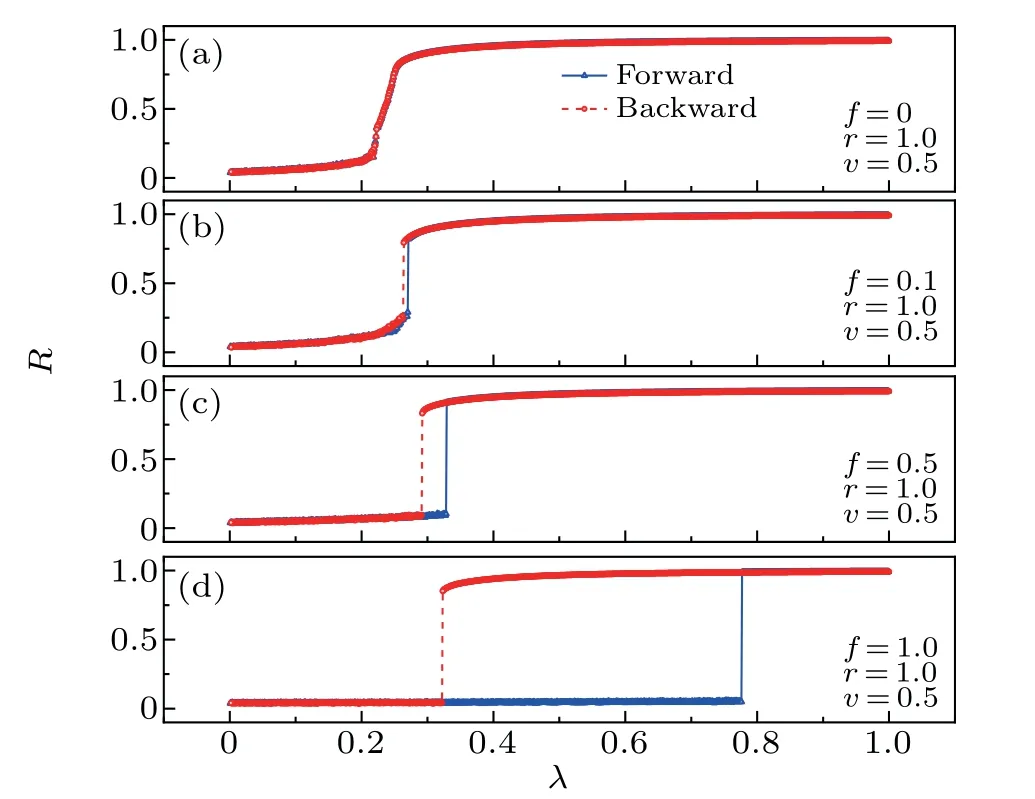
Fig.1. The transition to synchronization. R versus λ for different values of f;I fix N=500,δλ =0.001 and natural frequency follows random distribution in[-π,π]. The values used for the other parameters are reported in four plots. In all plots,the blue triangles and solid lines represent forward transition,while the red circles and dashed lines represent backward transition.

The first step is to study the effect of the positive feedback ofRon the phase transition. I divided the oscillators into the original oscillators and the oscillators regulated by the positive feedback mechanism and studied the effect of the positive feedback mechanism on the synchronization mode. The simulations are reported in Fig. 1 and reveal that controlling the actual coupling strength of the oscillator (also known as the effective coupling strength) using the global-order parameter can indeed lead to explosive synchronization (namely, phase transition is abrupt and discontinuous, accompanied by the hysteresis loop).

In Fig. 1, the curves of the dependences of the globalorder parameterRand global coupling strengthλfor forward transition(FW)and backward transition(BW)are reported for four values off.I setL=10(I fixed the value ofLin all simulations of this study,for the sake of simplicity),v=0.5,r=1,δλ=0.001 in Figs. 1(a)-1(d). And the natural frequenciesωof all the oscillators are uniformly distributed in [-π,π].It is clearly shown that the continuous transitions(second order)occur when PF is absent(i.e.,f=0). The two curves of FW and BW coincide completely. By contrast, the explosive synchronization emerges when I add the fraction of controlled oscillators in Figs. 1(b)-1(d). When some oscillators in the system are controlled by the positive feedback mechanism,the phase transition is first order and discontinuous,and a hysteresis loop also appears between the forward-phase transition and backward-phase transition.In fact,when the positive feedback effect does not exist,the phase transition is a second-order and continuous-phase transition. By comparing with Figs. 1(a)-1(d), I conclude that the positive feedback can induce explosive synchronization with a hysteresis loop,and increasing the value offleads to the increase in the width of hysteresis loopd. However,the critical coupling strength of the forward transition (i.e., the state changes from the incoherent state to the synchronized state)λcFincreases with the increase inf. I infer that this is because when oscillators are controlled by the global-order parameter of the system, it is difficult to form a local and small synchronous community in the system. Thus,the positive feedback is also a kind of inhibition. Only when the coupling strength increases until the critical value is exceeded, the explosive transition suddenly occurs. Therefore,the larger the value offis, the greater the coupling strength that is needed for transition.

Fig.2.The forward transition to synchronization for two values of f (f =0.1 for(a),(c); f =1.0 for(b),(d)). The top row panels and bottom panels display the curves of R versus λ and effective frequency ωeffi versus λ,respectively. The other parameters are the same as those in Fig.1.

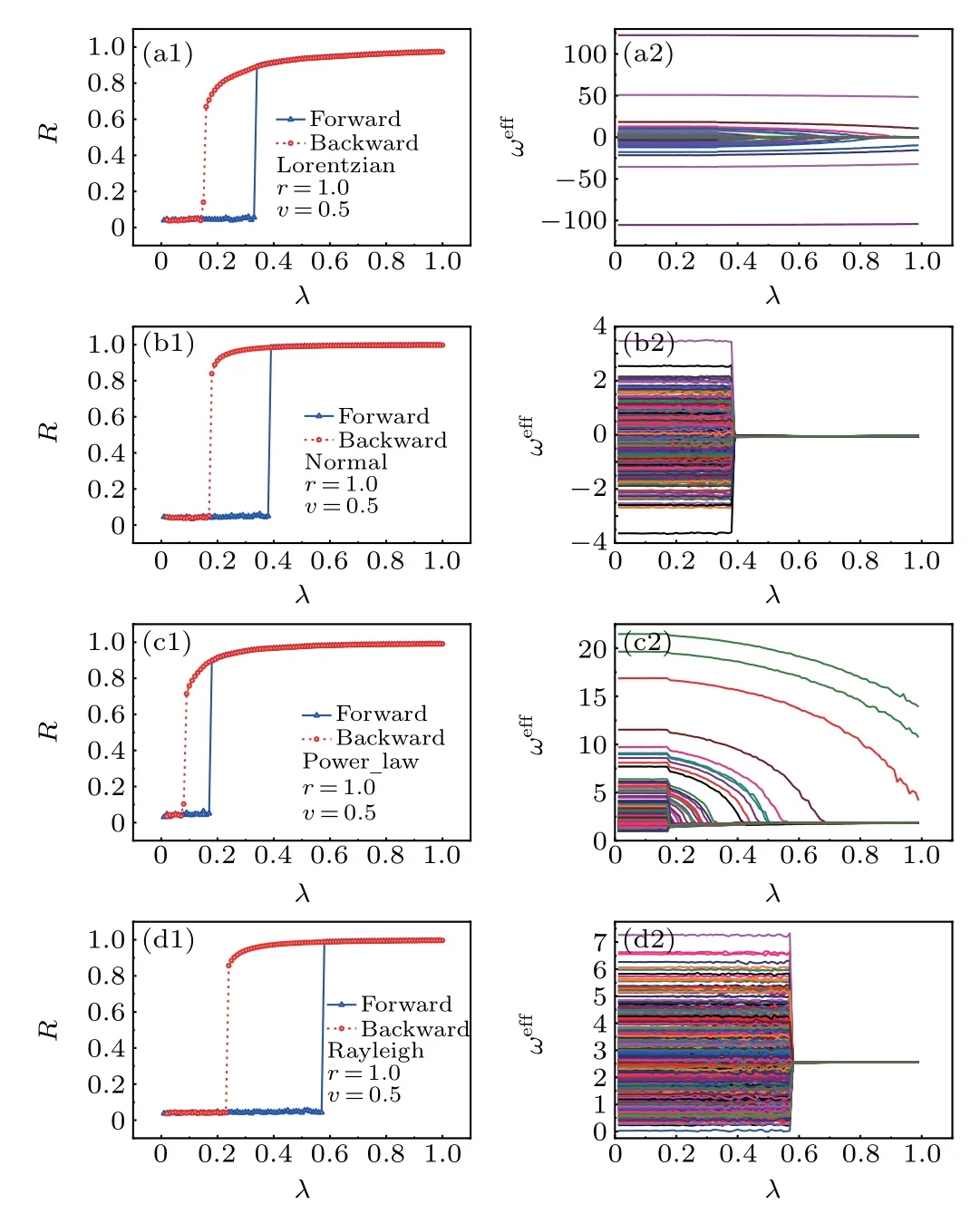
Fig. 3. The panels in the left column and right column display the relationships of R versus λ and ωeffi versus λ, respectively. We focus on two symmetric distributions g(ω), such as normal distribution and Lorentzian distribution, and two asymmetric g(ω), such as power-law distribution and Rayleigh distribution(see text for detail parameters).

In many natural instances, the structures of networks always change constantly. Previous studies have shown that explosive synchronization is closely related to the network structure. Thus,I study the communication radii of the mobile oscillators,which are the inherent parameters of parameters and affect the topology of the network. To understand the role that different values of the communication radiusrplay in changing transition behavior, I alter the value of the communication radiusrand plot curves ofRversusλfor selectedr(0.4,0.6,0.8,1.2) in Fig. 4. I fixδλ=0.01, and the other parameters are the same as those in Fig. 1(d). Forr=0.4,synchronization does not occur whenR ≈0, although I increase the coupling strength to 2. I deduce that the positive feedback mechanism of the order parameter prevents the synchronization in our model. I setf=0 again, and the other parameters remain unchanged. The insert depicts the relation of the global-order parameter and the coupling strength.The system reaches synchronization whenf=0;however,the phase transition is continuous. In the dynamic network model,rcan determine the critical connectivity of the network. ForN=500,L=10,the critical communication radiusrc≈0.54((N-1)πrc/L2≈4.51[38])if all nodes own neighbors in the single time stept. Due to the oscillators’ motion, the system can also reach synchronization when PF is absent. However,it is hard for the system to synchronize under the positive feedback and inhibition of the global-order parameterR. When the communication radiusrexceedsrc, I see that ES transition emerges in Figs.4(b)-4(d). I also notice that the critical coupling strengthλcFand loop size of hysteresisdboth decrease with the increase inr. This phenomenon may come from the fact that a larger value ofrleads to the oscillator having more neighbors, so it is easier for each oscillator to synchronize with their own neighbors and the system needs less coupling strength to synchronize.

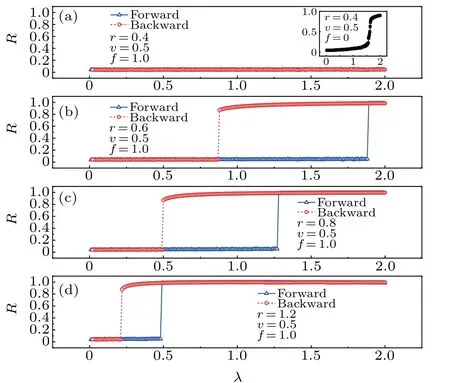
Fig.4. Dependence of the global-order parameter R versus coupling strength λ in forward transition(blue open triangle)and backward transition(red open circle), for different values of the communication radius r ((a) r=0.4; (b)r=0.6; (c) r=0.8; (d) r=1.2), when N =500 and the natural frequency follows random distribution. The insert in panel (a) reports the dependence of the global-order parameter and coupling strength when f =0.

4. Conclusion

In this article, I have presented the Kuramoto model within a dynamic network framework, wherein the oscillators’ coupling strength is controlled by positive feedback of the global-order parameter of the whole system. The explosive synchronization transition behavior can be controlled by simply adjusting the fraction of controlled oscillators.And the loop size of the hysteresis increases with the increase in the fraction of controlled oscillators. However, the transition is continuous(second-order transition without a hysteresis loop)when positive feedback of the global-order parameter is completely absent. By focusing on different probability density distributions of natural frequency, I further find that, whether the frequency distribution of nodes is symmetrical or not,this does not affect the synchronization behavior of the system.The effective frequencies of all oscillators get locked to the average value of the natural frequencies when the system reaches full synchronization.Lastly,I explore the role that the communication radius plays in ES transition. I note that a larger communication radius contributes a smaller loop size and transition cannot occur if the value ofris less than the critical communication radius in our model. Moreover, the system cannot reach synchronization by second-order phase transition,in our model, whenr

Acknowledgement

Project supported by the Natural Science Foundation of Jiangsu Province,China(Grant No.20KJB470030).