Three-dimensional clogging structures of granular spheres near hopper orifice

Jing Yang(杨敬), Dianjinfeng Gong(宫殿锦丰), Xiaoxue Wang(汪晓雪), Zhichao Wang(王志超),Jianqi Li(李建奇), Bingwen Hu(胡炳文), and Chengjie Xia(夏成杰)

Shanghai Key Laboratory of Magnetic Resonance,School of Physics and Electronic Science,East China Normal University,Shanghai 200241,China

Keywords: granular materials,clogging,magnetic resonance imaging

1. Introduction

Granular materials are ubiquitous in industrial applications and daily life, which may exhibit behaviors of both complex fluids and marginal solids under different external conditions.[1,2]The commonly-observed clogging phenomenon of granular particles is essentially a spontaneous jamming transition from a flowing state to a mechanicallystable static state,[3-5]which have aroused great interest from both industry and physics community.Granular material clogs when flowing through a narrow outlet in a statistical way.[6]Clogging and related jamming phenomena are ubiquitous not only in granular systems but also in other systems, including colloidal suspensions,[7,8]self-driven active materials,[9-11]and microbes,[12]etc. A flow of granular particles clogs due to the formation of a clogging structure near the orifice with some typical geometry that sustains its overhead loading. The probability of forming such a clogging structure depends on the hopper geometry,[13-15]properties of granular particles including shapes, frictions, and polydispersity,[16,17]as well as other external control parameters affecting the kinematics of granular flow.[18-22]In a two-dimensional (2D) model system of hard disks, an arch-like clogging structure has been observed, and its formation is mapped onto a restricted selfavoiding random walk to estimate the clogging probability using a pure geometry-based model.[23,24]Furthermore, nonpermanent clogging under external perturbations has been attributed to the existence of “defects” in arch structures,[25]and the associated non-ergodic unclogging dynamics has been modeled as a random exploration out of a potential basin in the landscape of arch configurations.[26-29]All these previous works emphasize the importance of the geometry of clogging structures, but whether the established concepts in these probabilistic models are independent of the spatial dimension remains untested. For three-dimensional (3D) granular materials, the lack of knowledge about the statistical geometric properties of the clogging structure renders a quantitative modeling of their clogging transition and discharging process difficult. Specifically, although it is reasonable to presume a dome-like 3D clogging structure by analogy with its 2D counterpart, the geometry of a 3D clogging structure, which is supposed to be a complex network, is much more complicated to be characterized than the one-dimensional(1D)arch in 2D case. Therefore,a systematic characterization of the arrangements of granular particles blocking the orifice based on various imaging experiments is necessary,[30,31]which should form a structural foundation to validate and generalize current models,and even to help understanding other non-granular 3D systems in the light of a general clogging phase diagram.[32]

In this work, dome-like clogging structures are reconstructed and identified with the help of magnetic resonance imaging (MRI) techniques, and their geometric and topological properties are quantified. It turns out that 3D clogging structures are distributed on a slightly flattened hemispherical surface, and are majorly composed of chain-like linear structures associated with a certain correlation length, which clearly manifest characteristics of mutual-stabilization and load-bearing. These observations allow us to form a simple phenomenological model to express the average size of clogging structures as a function of outlet size and shape,which is crucial in predicting clogging probability and avalanche sizes during silo discharging.[33-36]

The current paper is organized as follows. In Section 2,we introduce the clogging experiment and image processing method used to reconstruct the packing. In Section 3, we demonstrate various structural characterizations of the clogging structures. In Section 4, we provide a simple model for the clogging structure sizes. Concluding remarks are given in Section 5.

2. Materials and experiments

Granular particles used in this work are hollow plastic spheres filled with edible gelatin. The magnetic resonance signals are contributed mostly by protons in water molecules of the gelatin, so that the internal part of every sphere appears bright in magnetic resonance images, which enables a straightforward labelling of all spheres with image processing methods (Fig. 1(a)). The average diameter of these spheres isd= 15.78±0.07 mm. Hoppers with a zero slop angleαslope=0°and eight different orifice diametersDoutare used:fromDout=31.26 mm≈2dtoDout=59.09 mm≈3.75dat an interval of every 0.25d,as well as another three hoppers with a fixedDout=3dand three different slop angles:αslope=30°,45°, and 60°. The hoppers are made of polyvinyl chloride.The friction coefficient between a spheres is measured to be 0.43±0.02 (with a method introduced in Ref. [37]), and the friction coefficient between a sphere and a hopper surfaces is 0.40±0.09. These hoppers can be attached to a cylindrical container with an inner diameter of 19 cm≈12.0dand a height of 18 cm≈11.4d. During each experimental trial,the hopper and container were first attached to an additional large tube from above. Then,more than 1800 spheres were rapidly poured into the tube,and filled the container and hopper with a closed outlet to a height of about 14d. Next, the outlet was left open to discharge the spheres until a spontaneous clogging occurs. Typically, the number of spheres that flew out of the hopper before clogging was several hundred,and about 1200 spheres on average remained in the hopper and container,corresponding to a packing of about 10din height. During the pouring process,the hopper and container were steadily placed on the ground with no external vibration exerted. Data of two kinds of cases were discarded as the flow field and/or packing states before clogging might not be stationary and representative: (i) only few particles just at the orifice drop out while the remaining particles has already formed a clogged structure with no movements at all;(ii)height of the remaining packing above the orifice after clogging is lower than about 5d. The temperature and relative humidity of the lab was controlled to be around 20°C and 50%.

Fig.1. (a)Slices on two orthogonal planes of a raw magnetic resonance image,with part of the reconstructed packing structures superimposed.(b)A schematic diagram of the hopper geometry and the method to identify clogging structures: the shaded area near the orifice represents a free volume in which a sphere can move continuously without particle overlapping,and the yellow spheres outlining the upper boundary of this region compose the clogging structure. [(c)and(d)]Two reconstructed packing structures with(c)Dout=3.5d,αslope=0° and(d)Dout=3d,αslope=60°,in which the constituent spheres of clogging structures are highlighted with a golden color. [(e)and(f)]The same reconstructed structures as those in panels(c)and(d)viewed upward through orifices. [(g)and(h)]Average clogging size〈Nclog〉as a function of(g)orifice diameter Dout and (h) hopper slope angle αslope. The error-bar on each data point represents a 75% confidence interval, and are basically proportional to the standard variance of Nclog. The solid lines represent results of theoretical model according to Eqs.(3)and(4). A schematic diagram of the method to estimate sizes of clogging structures in hoppers with non-zero slope angles is shown in the inset of panel(h).

The clogged packing structures were then scanned with a 3T MRI system (MAGNETOM Prisma Fit; Siemens Healthcare,Erlangen,Germany),using a spoiled gradient echo scanning sequence (Turbo-FLASH),[38]and a parallel acquisition technique(GRAPPA),[39]and were finally reconstructed using image processing methods(Figs.1(c)-1(f)). The spatial resolution of the MRI is 1 mm/pixel,and the average uncertainty of sphere centroids is estimated to be around 6%of the diameter.It is observed that spheres near container boundary form layered structures,which are discarded in the following analyses.For each hopper,the aforementioned trials are repeated for at least six times for better statistics: a total of 75 sets of packing structures were analyzed for eleven different outlets. The average packing fraction of packing structures away from the orifice is 0.599±0.005. Contacts between spheres are identified using an error-function fitting method,[40]and the average contact number is calculated to be 5.30±0.05.

In reconstructed packing structures, a layer of spheres that block the orifice can be clearly observed as shown in Figs. 1(c)-1(f). But compared with the one-dimensional arches in 2D disk systems which can be identified instinctively, a rigorous definition for this 3D clogging structures is prerequisite to analyze their properties. To this end,we come up with the following operational definition (as illustrated in Fig.1(b)). First,a free volume near the hopper orifice is identified which comprises all points that are at least 1daway from the centroids of any spheres. By definition, this free volume can accommodate another sphere with a diameter ofdwithout particle overlapping. Then, all spheres whose centroids are 1daway from the boundary of this free volume is defined to compose the clogging structure. Apparently, if the positions of all particles in the clogging structure are fixed, there’s no way to move any other spheres in the packing continuously out through the orifice without penetrating these blocking spheres.This method rules out some extremely concave clogging structures which are very likely to be mechanically unstable,unless the interparticle friction coefficient is unrealistically large.For example, as shown in the schematic diagram (Fig. 1(b)), assuming that particles 3 squeezes in between particles 1 and 2 by slightly separating them,it would not be identified as a part of the clogging structure. Therefore, this definition is practically compatible with the arches identified in granular disk 2D systems. Clogging structures of 2D monodispersed disks would be identical to the arches near hopper outlet if identified following the procedures introduced in this work, as long as all angles between connections of adjacent contacts are larger than 120°. The probability of having contact angles smaller than 120°is indeed negligible as shown in Ref.[25].

3. Experimental results

We first study the dependences of the structure sizeNclog,i.e.,number of particles within each clogging structure,on orifice diameter and hopper angle. According to a simple geometric consideration, the projection area of clogging structures over the orifice should scale asD2out, and therefore, a plausible quadratic relationship between〈Nclog〉and orifice diameterDout,i.e.,〈Nclog〉∝D2outcan be inferred. However,interestingly, a linear relation has been observed in our system(Fig.1(g)),which are actually more similar to that in the 2D systems.[14,24,41]We propose that this counter-intuitive linear relation stems from an intrinsic correlation within clogging structures due to the mechanical stability requirement,and its length scale is comparable with the orifice diameter. For a strongly correlated clogging structure,a quadratic model associated with covering the orifice with randomly-placed spheres would be unsuitable. For hoppers with non-zero slope angles,a conventional decreasing〈Nclog〉with increasingαslopeis observed (Fig. 1(h)).[14]From a mechanical point of view, this stems from the finite friction coefficient between hopper inner surface and particles: the maximum vertical component of a fully activated frictional force depends onαslope, which sets an upper bound of the size of clogging structure that can be supported by the hopper’s inner wall. In Section 4, we introduce a phenomenological model incorporating both the structural correlation and hopper boundary condition to account for the dependences of〈Nclog〉onDoutandαslope. Furthermore,we notice that the standard variance ofNclogdecreases withαslope, while no clear dependence onDoutcan be observed.We propose that this is because a larger hopper slope imposes a stronger constraint on the shape and size of clogging structures against their intrinsic fluctuations with the mechanical boundary condition.

To provide more information beyond the average sizes of clogging structures,[31]we further quantify the overall shape of the clogging structures using its inertia tensorM,the component of which is

Furthermore,to quantify the clogging structure shape,we define an aspect ratio as

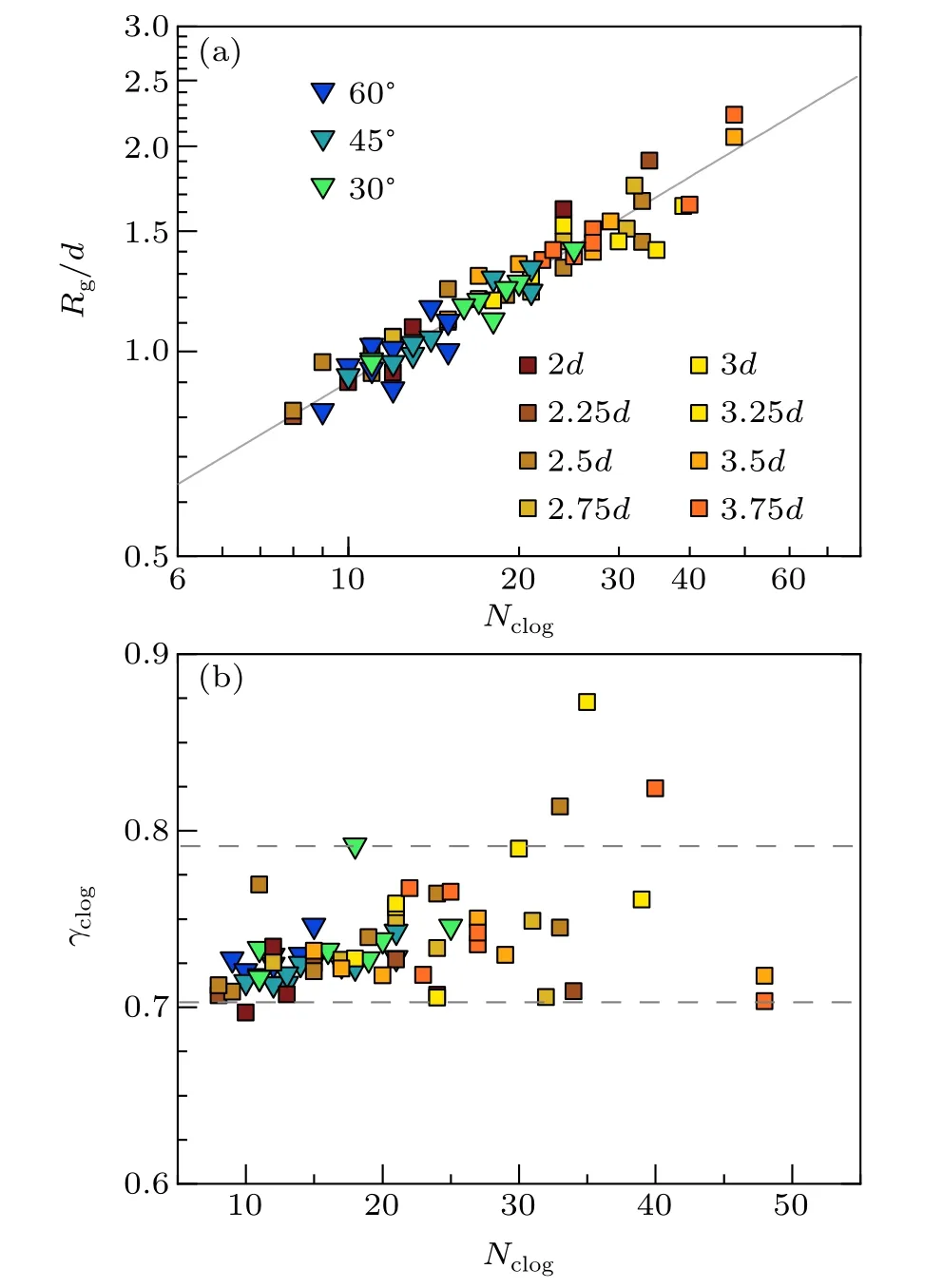
Fig. 2. (a) Radius of gyration and (b) aspect ratio of clogging structures as a function of structure size. Each point represents a clogging structure in hoppers with different orifice diameters and/or slop angles. The solid line in panel (a) represent a scaling relationship: Rg =N1/2clog. The two horizontal dashed lines in panel (b) represent the aspect ratios of a homogeneous hemispherical shell(0.79)and a circular disk(0.71).

To further study the load-bearing properties which is expected to be encoded in the geometry of a clogging structure,we analyze the relative positions of contacting spheres in the packing by calculating: (i) a contact orientation angleθzbetween the gravity direction and a vector connecting the centroids of each pair of contacting spheres,and(ii)a three-point contact angleθcspanned by one sphere and two of its contacting neighbors(see insets of Fig.3). These angles are crucial for the establishment of statistical models predicting the clogging probability and for the force analyses of clogging structure stability,[23,25]and their variance is a key indicator of arch-breaking in two dimensions.[28,29]In Fig. 3, we demonstrate the distributions ofθzandθcfor two groups of particles:(a: the clogging structure group)those in clogging structures,and only contacting neighbors which are also in the clogging structure are included when calculatingθc, and (b: the background group)all particles in the packing apart from those in contact with the container and hopper. Distributions of clogging structures obtained in hopper with different orifices are averaged, as we have verified that the variations of the distributions whenDoutorαslopechanges are smaller than the fluctuations of different clogging structures over a fixed orifice. For particles in the background group,θzexhibits a uniform distribution, and in comparison, particles in clogging structures have a clear preference for larger values ofθz, that is, there are more contacts lying close to the horizontal plane. Similarly, particles in the clogging structure favorθcwith large values close to 180°, corresponding to a quasi-linear chainlike contact geometry,which is a clear feature of load-bearing structures in granular materials.[43]In addition,the peak at 60°of the distributionp(θc) of the clogging structure group is lower than that of the background group, which corresponds to a locally dense structure of an equilateral triangle formed by three contacting spheres. This further implies that contacting spheres in the clogging structure tend to form branch-like networks. Although similar analyses have been conducted for 2D arches,[41]only with the comparison with particles away from the orifice as proposed here,the uniqueness of clogging structures associated with their special mechanical status is revealed. This structural anisotropy also reminds us of the correspondence between strong force chains and arches identified in 2D systems.[44]

The aforementioned geometric features along with the implied requirements of load-bearing and mechanical stability suggest a possible close relationship between the clogging structure and mutually-stabilized bridge structures in jammed granular packings identified previously.[45]A bridge structure is a configuration of several contacting spheres satisfying the following three-point mutual-stability condition: one sphere is stabilized by a group of three contact neighbors if a vector from its centroid along the gravity direction goes through the triangle formed by the centroids of the three particles(i.e.,the triplet). Note that the triplet with the lowest centroid of mass is chosen if there exist more than one triplet satisfying above criteria.[46]Two spheres are mutually-stabilized if one of them rests on a triplet including the other one, andvice versa(see inset of Fig. 4(b)). We find that, for all pairs of contacts between spheres in the clogging structure, about 7.8% of them form mutually-stabilized configurations, and in comparison,for all contact pairs in the packing,this fraction is reduced to 5.2%. This difference verifies an enhanced cooperativity associated with the clogging structures. In addition, bridge structures have been identified in our packing,and we analyze the bridge size: number of spheres composing each bridge. Interestingly,the average size of bridges near the orifice is quite close to that of all bridges in the packing,and is basically independent ofDoutandαslope. Therefore,the average bridge size is determined by the global packing fraction alone,[45]and represents an intrinsic length scale associated with the cooperative stability.

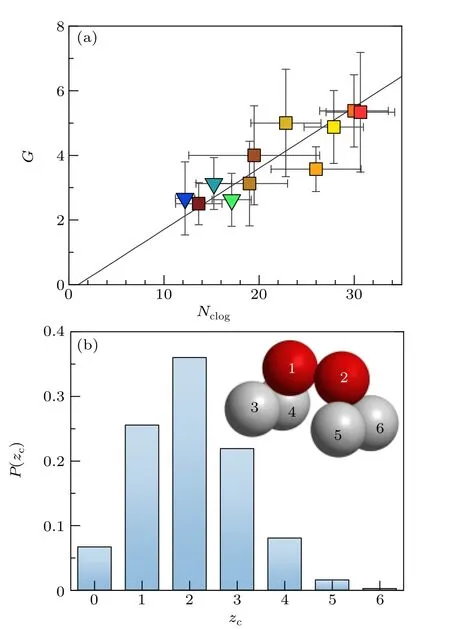
Fig. 4. (a) Genus of clogging structures versus structure size. The solid line represents G=0.19. (b)The probability distribution of contact number between constituent spheres of clogging structures,which have also been verified to be basically independent of hopper dimension. (Inset)A schematic diagram of a typical bridge structure:particle 1(2)is supported by particles 2,3,and 4(1,5,and 6),and therefore particles 1 and 2 are mutually stable.

4. Theoretical model

Last but not least, we present a simple model to account for the dependence of clogging structure size on hopper dimension based on above observations.As defined in Section 3,each bridge structure identified in the packing is a collection of mutually-stabilized spheres,while correlation between bridge structures should be relatively weak,since no pairs of spheres from two different bridges support each other. As a crude model, we propose that a clogging structure is composed by a few independent structural motifs of several spheres,such as the bridge structures defined above. On the other hand,a necessary condition for a blocked orifice is that there are at least about (2πDout/d)/2 spheres arranged along its periphery to prevent other spheres from flowing through it. Likewise,these spheres should be only very weakly-correlated since there is also no mutual-stability requirement between them. Therefore,we propose that the average number of independent motifs in one clogging structure is proportional to, if not very close to,the number of spheres at the periphery,so that a simple relationship between the average clogging structure size and orifice diameter:

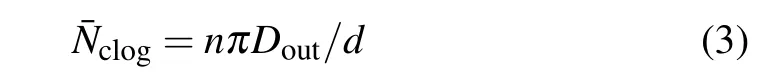
is obtained.The proportionality factorncorresponds to the average number of spheres associated with one structural motif in clogging structures,and should be quite close to the average number of spheres in one bridge structure. By fitting the experimental data(Fig.1(g)),we calculatento be 2.6±0.1. We also evaluate the average bridge size, which is the number of spheres composing all bridges in each packing divided by the number of bridges,and obtain a self-consistent average value of 2.4±0.1.

The foundation of above proportionality hypothesis is the structural correlation of spheres in clogging structures.This linear relationship therefore reinforces the conception that only strongly-correlated structures with load-bearing ability are selected during the flow process to eventually halt the flow.[36]Another direct corollary of this hypothesis is that there should be a typical largest orifice, beyond which clogging could hardly happen,since the area covered by spheres in the clogging structures increases much more slowly withDoutthan the orifice area. For a fixedαslope,this critical maximum diameter should be simply limited by this intrinsic correlation length,that is,the average bridge size.

This expression is consistent with the experimental results as shown in Fig. 1(h). A crude examination of results on the length of 2D arches suggests that above geometric model also works satisfactorily when modified to apply to the 2D case.[14]

5. Concluding remarks

Using MRI techniques and a series of structural quantification methods,the 3D clogging structures of granular spheres near hopper orifice have been systematically quantified. Clear geometric features associated with the load-bearing abilities of clogging structures have been revealed, and dependences of the size and shape of clogging structures on hopper dimensions have been studied. Despite that the overall characteristics is qualitatively similar to that of arches in 2D disk systems, the 3D clogging structure is found to be close to a branching network,so that it involves a complex combination of some elementary linear load-bearing motifs. The requirement of load-bearing for clogging structures inevitably introduces a correlation length,which is arguably the typical size of cooperatively-stable bridge structures. This is consistent with the quasi-linear strong force chains observed with 2D photoelastic granular disks,[47]which we suggest is the underlying mechanical reason why only configurations with specific geometric features identified here are selected out to form the clogging domes. Meanwhile,this correlation also implies that the formation of a clogging structure is not a random collection of independent spheres,but is associated with the dynamical cooperativity of the heterogeneous dense granular flow.Hypothetically,it is possible to identify precursory fluctuating structures in the flow prior to clogging with similar geometric features as the clogging structures, which should explain the stochastic nature of clogging.

Phenomenologically,a direct consequence of the correlation length of load-bearing structures being comparable to the orifice is the linear dependence of the clogging structure size on the orifice diameter,which is unexpected and non-trivial for 3D systems,and should be tested in future with more accuracy.We also propose that based on our observations,more sophisticated stochastic models may be established,such as a randomwalk percolation model on a hemispherical surface with an additional short-range correlation,to provide a solid structural mechanism for the clogging phenomenon of 3D granular

materials.

Acknowledgments

Project supported by the China Postdoctoral Science Foundation (Grant Nos. 2018M641957 and 2019T120319),the National Natural Science Foundation of China (Grant No.11904102),and the Fundamental Research Funds for the Central Universities,China.