Influence of Coulomb force between two electrons on double ionization of He-like atoms

Peipei Liu(刘培培), Yongfang Li(李永芳), and Jingtao Zhang(张敬涛)

Department of Physics,Shanghai Normal University,Shanghai 200234,China

Keywords: double ionization,Coulomb force,Coulomb-Volkov state,scattering theory

1. Introduction

Strong-field double ionization (SFDI) denotes that two bound electrons are released from atoms and molecules by the intense laser field.[1-4]This effect is important because it provides a prototype of electron correlation that widely exists in natural process. According to a three-step scenario,[5,6]the electron correlation was set up during the recollision process of the returned electron with the parent core, which enhances the double ionization rate significantly. In the past decades, this kind of the electron correlation has aroused extensive studies.[7-10]In this paper,we show that the Coulomb force between two electrons also enhances the double ionization rate notably.

Many treatments were developed to study the SFDI process in intense laser fields. The numerical solution to the timedependent Schrodinger equation method that was widely used in the study of single ionization, however, is limited in onedimension studies for double ionization because it is timeconsuming when two electrons are involved.[11]The classical ensemble method developed by Eberlyet al.became popular,owing to its simplicity and high efficiency.[12]The S-matrix treatment, developed by Fasialet al.,[13]presented an analytical formula of the double ionization rate. However, this formula is very complicated and time-consuming.

Nowadays, all the available treatments on the SFDI process regard intense laser field as a classical field,although the concept of photon is frequently involved.[13]In fact,quantum features do appear in experimental observation on SFDI.One demonstration lies in the sum energy spectrum of two electrons. It was observed that a series of peaks, with the interval of one photon,appear in the sum-energy spectrum of two electrons. This feature is significantly similar to the observation on above-threshold ionization spectra,[6,14,15]but cannot be explained in terms of the interference of wavepacket that is separated by half optical cycle in the birth time. Thus,the discrete peaks in the photoelectron spectra strongly indicate the quantum feature of the laser fields. This suggests one to treat the laser field as a quantized one.

In this paper,the eigenstate of two electrons in an intense quantum field is derived, by which we obtain a simple analytical formula of the double ionization rate. The motion of two electrons moving in an quantum laser field is, actually, a three-body problem, i.e., two electrons and all photons act as the third body.The eigenstate of an electron in the laser field is the known Volkov state,but the Coulomb interaction between two electrons introduces a singularity and becomes dominant in the electron collision process. By introducing the center-ofmass(COM)coordinate and the relative coordinate,we divide the state of the two electrons in the laser field into the inner and outer degrees of freedom.The inner degree of freedom describes the relative motion of two electrons and can be treated as a quasiparticle of half electron mass moving in a Coulomb field. Its state is known as the repulsive Coulomb state. The outer degree of freedom describes a quasiparticle moving in an intense laser field and its state can be described by the Volkov state. Such a treatment was also used by Faisalet al.,[16]but the laser field is quantized in our treatment. The quantum field Volkov states have well-defined eigenenergy, which make it possible to study the photoionization from the energy viewpoint.

Using the derived Coulomb-Volkov state, we obtain an analytical formula of the double ionization rate in the frame of scattering theory,by which we discuss the effect of Coulomb repulsive force between two electrons. We will show that the Coulomb force enhances the ionization rate of high-energy electrons by more than two orders of magnitude but suppresses greatly the ionization rate of the lowest-energy electrons.

2. Coulomb–Volkov state of two electrons

For an electron moving in an intense laser field,the quantum-field Volkov state is the eigenstate of the Schrodinger-like equation.[17-19]In this paper,we firstly show how to divide the Hamiltonian into two parts through a series of transformations,then start from the Schroding-like equation to get the two-electron quantum-field Volkov state in singlemode laser fields.

The eigen-equation of two electrons of massmemoving in an intense laser field is given by (atomic units ¯h=me=|e|=1 are used throughout this paper)

in which-i∇iandriare the momentum operator and the position of theith electron with respect to the core, andr12=|r1-r2| is the distance between the two electrons. In this Hamiltonian,the Coulomb force between the two electrons is independent of the laser field, which satisfies the principle of independent action of forces. This treatment holds in the nonrelativistic case,where both the intensity of the laser field and the velocity of each electron are not too high. This Hamiltonian is widely used in other theoretical treatments.[16,20-22]The vector potential of a laser field is

whereξmonitors the degree of ellipticity of the laser field,such thatξ=0 corresponds to linear polarization andξ=π/2 to circular polarization. The phase angleθis the initial phase value.[18]

In order to eliminate the coordinate dependence of the vector potential,we define a unitary operator as follows:

Since the Coulomb force is a central field and depends on the relative distance between the two electrons, we introduce the relative coordinate to deal with the relative motion of the two electrons,and introduce the center-of-mass(COM)coordinate to describe the motion of the two electrons in the intense laser field. This is carried out by introducing the momentum operators[15]

2.1. Repulsive Coulomb wave function

The eigenstate ofHCis a repulsive Coulomb wave function given by[23,24]

where1F1is the confluent hypergeometric function,v=1/a0pis a dimensionless parameter depending on the relative momentum of the two electrons,and

in which Γ(x) is the Euler gamma function, anda0is the Bohr radius. For the quasiparticle of reduced mass 1/2meand chargee,a0=2.0 a.u. The Coulomb wave function is characterized by the momentump,so it varies withvnotably.Whenv=0,N(0)=1.0 and1F1(0,1,x)=1.0, the Coulomb wave function reduces to the electronic plane wave, and then the Coulomb force becomes negligible. Whenv ≤1,this part wave function decreases whenrincreases while keeps positive and the real part is always far larger than the imaginary part. Whenv>1, these features lost, but the absolute value decreases fast. Thus, whenv →∞, the Coulomb wave function also reduces to the electronic plane wave.The dimensionless parametervdenotes the Coulomb effects between the two electrons in momentum space.

2.2. Quantum-field Volkov state

For Hamiltonian(8),it is quite similar to the one that describes an electron moving in a quantum laser field.The difference lies in both the charge and the mass of the quasiparticle are doubled. The motion is described by the known Volkov state expressed as

2.3. Final wave function

Combining the above results, the eigenstate of the total Hamiltonian can be expressed as

3. Double ionization rate formulae

In order to analyze the double ionization process in more details,we regard the CV state obtained above as the final sate,and derive the transition matrix element of the double ionization in the strong laser field.

The interaction Hamiltonian of a two-electron atom with the intense laser field is given by

in which the first two terms denote the interaction of the two electrons with the laser field, the last term is the selfinteraction of the laser filed. According to the scattering theory,the transition matrix element can be expressed as

wherej=ni-n. The final wave function for two-electron moving in an intense-laser field is given by Eq. (13) and the initial wave function of He-like atoms is given by[25]

whereN= 1.476 is the normalization constant, andα=3.716/a0andβ=-0.255/a0are two parameters of momentum dimension. Compared with the hydrogen-like wave functions, it is easy to find that the parameterβplays the role of the inverse Bohr radius. Becauserdenotes the relative distance of the two electrons in the bound state of He-like atoms,the Coulomb effect varies withβ.

The overlapping factor in Eq. (15) is derived in the following.

3.1. Integration over R

This part describes the dynamics of the quasiparticle of mass 2meand charge 2ein the intense laser field.

3.2. Integration over r

which is the hydrogen-like 1s wave function in momentum space, similar to that in Eq. (16). This relation also indicates that the quantityI(v)has the dimension of wave function in the momentum space, thus we term it as the Coulomb-corrected wave function.

3.3. The ionization rate formula

Using the above formulas, we express the transition matrix element as

by which the total double ionization rate can be expressed as

4. Effect of Coulomb expansion between electrons

The single-electron multiphoton ionization is determined mainly by the GPB functions, including its order and two arguments. These quantities, in turn, are determined by three dimensionless parameters, i.e., the number of absorbed photonsjfor ionization, the binding numberεb=Ip/ω, and the ponderomotive parameterup. It has been shown that the electronic dynamics are equivalent in different laser fields when those three parameters are kept unchanged,thus a scaling law is established that is verified to be hold in multiple electronphoton interaction processes.

For double ionization, the electronic dynamics is determined by two factors. One is for the multiple photoionization of the quasiparticle in the intense laser field and works via the GPB function,which is similar to that in the single ionization case. The other is for the Coulomb repulsion between two electrons and changes the double ionization rate mainly via the quantity in Eq.(21). The Coulomb force between the two electrons plays a key role in double ionization process, thus we focus on its influence in the following.

The effect of the Coulomb force between the two electrons lies mainly in the quantityI(v) that is independent of the direction ofpj. In order to identify the Coulomb effect,we calculateI(v) for different values ofβ. Figure 1 depicts the module ofI(v)as a function ofvfor severalβ. From this figure we see that whenβis small, the module ofI(v) increases firstly,reaches a maximum,and then decreases. However, whenβis larger than 0.5, the module ofI(v) increases monotonically withv. Whenvis smaller than 2.0, all curves increase quickly;however,whenvis larger than 6.0,all curves change slowly. For He-like atoms, the parameterβis about 0.13(±0.02), thus there is an optimal value ofvwhere the Coulomb effect is maximal. For He atom,β=0.1275 and the optimalv=2.725.

Next we show the variation of the double ionization rate withvin given processes. In a givenj-photon process, the double ionization rate is determined mainly by two factors,i.e.,I(v) and the GPB functionχ-j(zc,zs). The first factor is a function ofv, and it changes slightly whenvis large, as shown in Fig. 1. This indicates that whenp1-p2is large enough, the Coulomb effect is negligible. The second factor,i.e., the GPB function term, also varies withv, because the first argument of the GPB function, i.e.,zcin Eq. (12), depends onPwhile the latter varies with|pj|≡1/(a0v)through the relation in Eq. (22). Whenvis large, the momentumPtends to its maximum,and hence the GPB function keeps constant almost. Subsequently, whenvis large, the double ionization rate changes slightly withv. In the following discussion, we focus on the case ofv<20, which corresponds to|p1-p2|>0.05 a.u.

Fig. 1. Variation of the Coulomb-corrected wave function I(v) with v for He-like atoms with several β.

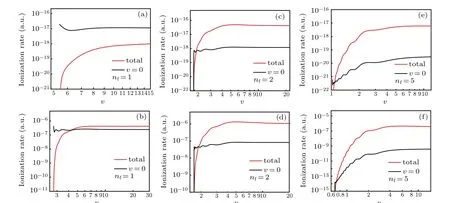
Fig.2. Variation of the double ionization rate with v in different processes: (a)-(d)for the first and the second ATI peaks,(e)and(f)for the 5th and the 10th ATI peaks,respectively. The laser field is of wavelength 800 nm and intensity 5.0×1013 W/cm2 (upper)and 2.0×1014 W/cm2(lower),respectively. The quantity nf denotes the ATI order.

Figure 2 show the variation of the calculated double ionization rate withvin several processes. Generally,the double ionization rate increases distinctively whenv<5, but keeps almost constant whenv>10. Such a pattern is quite similar to that ofI(v),indicating that the change is mainly caused byI(v). In order to identify the effect of Coulomb repulsive force, we also calculate the ionization rate without the Coulomb force. This is carried out by settingv=0 in the transition matrix element. The results are also shown in Fig. 2.The comparison of two curves discloses clearly the influence of the Coulomb force. The change can be identified into two categories. One is that the double ionization rate is notably enhanced whenvis large. Generally,the enhancement reaches about three orders of magnitude. The other is the suppression in the double ionization rate whenvis small. Because the Coulomb repulsive force shares a part of energy that the electrons absorbed from the light field, it increases the ionization threshold and decreases the ionization rate. The suppression effect becomes notable only for the low order photoelectron peaks formed by the weak laser fields, as shown in Fig. 2(a)for the first peak formed in the 5.0×1013W/cm2field,where the suppression effect is notable even whenvis large. In other figures, the suppression effect is notable only at the starting point of abscissa axis.

Finally, we show the influence of the Coulomb force on the overall ionization rate. The double ionization rate increases nonlinearly with the laser intensity, as shown in Fig.3 forλ=800 nm and 400 nm,respectively. Without the Coulomb force, i.e., forv=0, the double ionization rate decreases about one order of magnitude. This suggests that the Coulomb force between two electrons effectively increases the double ionization rate.

Fig. 3. Variation of the double ionization rate with laser intensity for laser wavelength 800 nm (black lines)and 400 nm (red lines), respectively. The dot-dashed lines are for the cases of v=0. The inset depicts the comparison in low-intensity regime.

5. Conclusion

In summary, we have derived the eigenstate of two electrons in an intense laser field. It is found that a repulsive Coulomb state can be used to describe the relative motion of the two electrons,and that the quantum-field Volkov states can be used to describe the center-of-mass motion of the two electrons in the intense field. Using the CV state,we derive a simple analytical formula of the double ionization rate,by which the effect of the Coulomb force between two electrons is studied. We have shown that the Coulomb force enhances the ionization rate of high-energy electrons by more than two orders of magnitude but suppresses greatly the ionization rate of the lowest-energy electrons.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11674231 and 12074261)and the Shanghai Natural Science Foundation, China (Grant No.20ZR1441600).