基于紧缩McCormick方法的热电联合系统优化调度策略
2022-01-22邓莉荣孙宏斌李宝聚孙勇阳天舒张璇
邓莉荣,孙宏斌,b,李宝聚,孙勇,阳天舒,张璇,
aTsinghua-Berkeley Shenzhen Institute,Tsinghua University,Shenzhen 518055,China
bState Key Laboratory of Power Systems,Department of Electrical Engineering,Tsinghua University,Beijing 100084,China
cState Grid Jilin Electric Power Supply Co.,Ltd.,Changchun 130000,China
dElectrical College,Harbin Institute of Technology,Harbin 150006,China
质量流量可调的热电联合系统可以提高能源系统的灵活性、经济性和可持续发展能力。但是,考虑质量流量可调的热电联合系统的优化运行问题是一个高度非凸非线性的问题,主要体现在热力网络模型中的双线性项,即质量流量和节点温度的乘积。现有的方法,如非线性优化、广义Benders分解方法和凸松弛技术等,在求解质量和计算性能上仍然存在不足。为了解决这一问题,本文首先建立了基于质量-流量调节的区域供热网络的基础模型,并通过等效变换和变量代换对基础模型进行了重构。该重构模型减少了非凸约束和双线性项,而且在不失去最优性的前提下,加快了求解过程。然后,文中分别建立了电力网络模型和能源模型,结合之前构造的供热网络模型,建立起热电联合系统优化调度模型。为了松弛联合调度模型中剩余的双线性项,文中采用McCormick包络的凸松弛方法,得到了联合调度模型的目标函数下界。为了提高McCormick松弛的质量,文中提出了一种紧缩McCormick的方法:首先,采用分段McCormick技术,将双线性项中一个变量的可行域划分为几个不相交的区域,通过求解此优化问题可以选出最优解所在的区域,从而缩小了被划分变量的可行域;然后,提出了一种启发式的边界收缩算法来进一步压缩分段McCormick技术得到的缩小版可行域,并恢复了此最优解附近的可行解。算例分析表明,与原对偶内点法和求得全局最优解的双线性求解器提供的方法相比,本文提出的紧缩McCormick方法能快速求解热电联合运行问题,得到令人满意的兼具最优性和可行性的调度结果。
热电联合系统
凸松弛
优化运行
McCormick包络
1.引言
1.1.背景及动机
电力系统(EPS)是国家能源供应的重要组成部分,决策者也逐渐意识到供热在能源系统中同样起着关键作用。国际能源署的报告称,全球一半以上的能源用于取暖[1]。相比人口低密度地区常用的供热选择,如私人热泵、燃气锅炉、太阳能供暖和电供暖等,人口高密度地区的大部分供热来自区域供热系统(DHS)。尽管不同国家和地区使用这些供热方式的比例不同,但区域供热的方式已被证实是非常节能的[2]。
电力和热能可以通过集中式能源生产和区域供热基础设施同时产生。一般来说,这两个大型能源系统——EPS和DHS,是通过热电联产(CHP)工厂和电转热设备紧密相连的。到2050年,CHP将为欧盟提供26%的电力。在丹麦,政府的目标是到2035年实现100%的可再生热能和电力生产[3]。预计在不久的将来,EPS和DHS在能源生产和消费过程中将在更大程度上相互影响。因此,热电联合系统的想法引起了从业者和研究人员的兴趣。
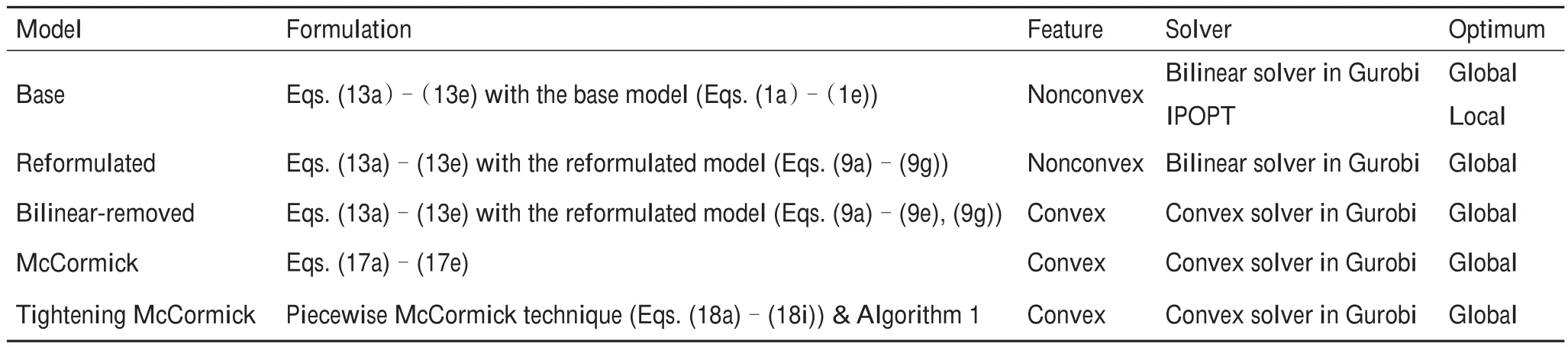
现在,关于热电联合系统不同方面的研究正在兴起,包括建模[4]、状态估计[5]、机组组合[6]、经济调度[7-9]、市场机制[10-11]和规划[12-13]等不同方面。其中,建模是商业化发展热电联合系统的基础与实质所在。尽管在过去的几十年里,研究人员对EPS建模已经进行了深入的研究,但大量关于DHS建模的研究仍在进行中。一般来说,DHS具有三种调节模式,如表1所示。质调节采用恒定质量流量和可变温度策略[7]。因此,相关优化问题中的约束变为线性问题,从而易于处理。然而,预先确定水力条件的情况可能不会得出经济的解决方案。相比之下,量调节保持恒定的供应温度,但调节质量流量。它更为灵活并且降低了成本,因为质量流量会根据热负荷的变化而变化,从而降低循环水泵的功耗。显然,同时调节温度和质量流量可以实现更高的经济效率和灵活性,这被称为质量-流量调节。到目前为止,对具有可变质量流量策略的综合能源系统运行的研究还很少[14-18]。此外,解决非凸和非线性网络流约束的高效且可扩展的算法仍在研究中。为此,本文提出了基于质量-流量调节的热电联合系统的凸模型和高效算法,期望通过该算法以较小的计算量找到全局最优或近似全局最优的可行解。

表1 DHS中的不同调节模式
1.2.文献综述
质量-流量调节的DHS建模属于池化问题[19]。池化问题是一个网络流问题,旨在找到在中间池中混合多个输入的最低成本方式,以便输出满足需求或某些要求的结果。混合输入涉及混合流量和特征的乘积。因此,池化问题就变成了一个双线性问题。在DHS建模中,非凸和非线性网络流增加了问题求解的难度。在非凸项中,由质量流量和节点温度的乘积得出的双线性项是很难处理的项之一。
目前处理DHS优化的双线性问题的研究成果可以分为四类:非线性规划方法、广义Benders分解、松弛方法和松弛紧缩方法。非线性规划方法,如内点法、序列线性规划和逐次二次规划[14],通常能够求解具有连续变量的非线性规划问题,并且易于使用现成的求解器实现。但是,这些方法只能找到局部解,当网络规模变大时,可能会出现收敛缓慢甚至收敛失败的情况。
广义Benders分解可以解决特定类型的非线性规划和混合整数非线性规划问题。为了处理质量流量和节点温度乘积的双线性,文献[15]提出了一种迭代算法:通过分别固定一组变量来求解另一组变量,迭代求解两个子问题直到收敛。但是,该方法不能保证所得解是全局最优解或局部最优解,其收敛性也有待进一步研究。
通常而言,松弛方法,如锥松弛[16-17]和多面体松弛[18],将原始非凸可行域扩大到凸的可行域。松弛后的问题变成凸问题的代价是牺牲了原问题解的可行性。松弛方法的性能很大程度上取决于松弛边界,边界越紧,松弛效果越好。这就产生了松弛紧缩方法,如文献[18-20]中所示。这种方法的核心原理是提供更紧的边界来增强松弛。在松弛紧缩方法中,分支定界法已经在最新版本的Gurobi,即Gurobi 9.0[21]的双线性求解器中成功使用,以处理双线性规划。Gurobi 9.0中的双线性求解器确保了全局最优解,并可用作评估其他方法最优性的基准。但是,在处理大规模问题时,此方法可能会收敛缓慢。
1.3.本文的贡献
本文首先通过等效变换和一阶泰勒展开重新构建了经典的质量-流量调节DHS优化模型。相比原始模型在每个非凸约束中具有两个双线性项,重构模型具有的双线性项更少;更具体地说,它减少了大约一半的双线性项。重构不仅确保了最优性,而且在降低原问题的计算复杂度方面具有一定优势。接下来,我们执行McCormick包络来凸化双线性约束,并得到重构模型的目标下界。为了提高McCormick松弛的质量,我们采用分段McCormick技术推导出双线性项更紧的上、下界来减少McCormick松弛后可行域的体积。分段McCormick技术将双线性项中一个变量的域划分为几个不相交的区域,并确定最优区域,从而收紧所选变量的界限。这样,就得到了原问题的强化下界解。针对强化下界解可能不可行的问题,我们建立了启发式的边界收缩算法,进一步缩紧了分段McCormick技术的加强下界,并采用迭代的方式获得附近的可行解。
相比非线性优化[14]和广义Benders分解[15],本文所提出的方法基于松弛和分段技术,具有更强的可扩展性,避免了局部不可行的问题。相比当前的松弛紧缩方法(如在Gurobi双线性求解器中实现的方法[21]),本文所提出的紧缩McCormick方法能够保证求解质量且减轻计算负担。
总而言之,本文有以下三个主要贡献:
(1)通过变量代换和等价变换,对具有质量-流量调节DHS模型的经典热电联合系统运行问题进行重构,大大降低了经典模型的双线性复杂度。
(2)基于重构模型,应用McCormick包络来松弛剩余的双线性项。为了减少松弛误差并缩紧McCormick包络边界,提出了分段McCormick技术。
(3)为了提高解的可行性,本文设计了一种边界收缩算法,通过对最新的最优结果施加扰动来缩紧分段Mc-Cormick包络的上下界。案例研究表明,分段McCormick技术与边界收缩算法两者相结合的紧缩McCormick方法可以快速得到满足实际运行需求的可行的较优解。鉴于其具有凸性,紧缩McCormick方法有望用于大规模热电联合系统优化,并且可以使用影子价格进行经济分析。
本文的其余部分安排如下:第2部分介绍了基于DHS基本模型和重构模型的联合系统运行问题;第3部分详细介绍了用于解决联合运行问题的凸松弛技术和紧缩Mc-Cormick方法;第4部分给出仿真算例;第5部分得出结论。
2.问题表述
热电联合系统由DHS和地区EPS组成。地区EPS是整个多区域互联电力系统的一部分,它有一个或多个接口与整个电力系统的其他部分进行电力交换。对于DHS建模,我们首先提出一个基本模型,这是一个没有任何松弛约束的非线性优化模型。然后,我们通过一阶泰勒展开和变量替换推导出DHS的等效重构模型。结果证明,重构模型减少了基础模型的非线性项;也就是说,基础模型中的双线性项减少了近一半。对于EPS的建模,我们采用考虑无功功率和电压幅值的状态无关线性潮流模型。连接两个系统的耦合元件是CHP机组。该运行问题具有多个目标,如最小化燃料成本、与其他互连电力系统的电力交易成本以及网络损耗。为了简单起见,我们分别为DHS和EPS构建了单时段模型。然后,我们将整个运行优化扩展到多时段,并在所有决策变量中添加表示时间的符号t。
2.1.区域供热系统建模
在质量-流量调节的辐射状区域供热网络中,我们通过循环泵调节质量流量。质量流量有大小和方向。本文假设质量流量的大小是可变的,而方向是固定的。这个假设是合理的,因为频繁的方向变化会导致供应的不稳定。
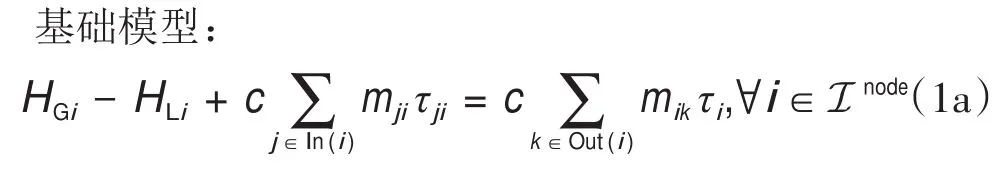
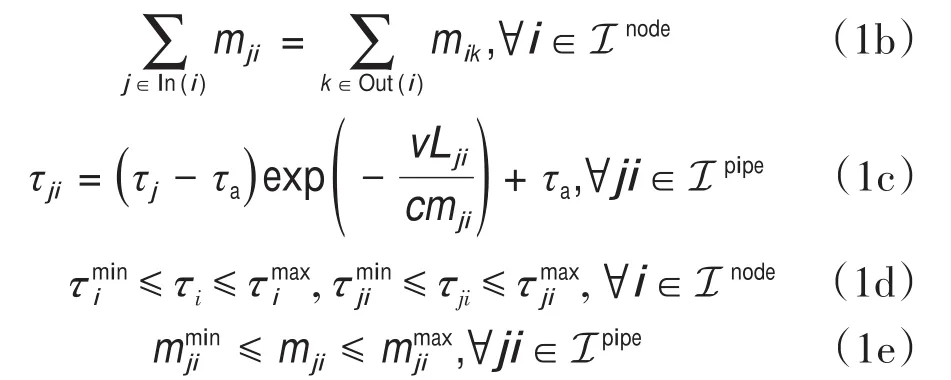
式中,HGi是节点i的产热量;HLi是节点i的热负荷;c是水的比热容;mji是热网管道中从节点j传输到节点i的水的质量流量;τi是节点i的出口温度;τji为节点j到节点i的管道出口温度;τa为环境温度;v为单位长度的传热系数;Lji为节点j到节点i的管道长度;为τji的下界/上界;是mji的下界/上界。In(i)是热网中流入节点i的节点索引集合,Out(i)是流出节点i的节点索引集合。Inode和Ipipe分别是热网中节点和管道的索引集合;ICHP是热电联产机组的索引集合;IHB是采暖锅炉(HB)的索引集合。等式(1a)定义节点热平衡。等式(1b)定义节点流量平衡。等式(1c)描述了在考虑热损失因素[22]的情况下,水温沿管道下降的过程。具体而言,管道出口温度τji取决于管道起点处的出口温度τj。如果管道长度较长,传热系数较大,或质量流量较小,则温降(以及热损失)就越为明显。等式(1d)是节点出口温度和管道出口温度的最小和最大操作限制。等式(1e)给出质量流量的最小和最大操作限制。要注意的是,可以将保持供应节点温度恒定的附加约束添加到基本模型中;这些将构成量调节模型,其计算复杂度与质量-流量调节模型相同。
2.2.DHS的重构模型
等式(1a)和等式(1c)使得DHS基础模型非凸。等式(1a)有双线性项mτ,等式(1c)具有指数函数exp(-vL/(cm))。
·为了处理双线性项,我们引入了辅助变量H=mτ。结果证明,这种变量替换减少了双线性项。
·为了处理指数函数项,我们使用一阶泰勒展开来近似方程(1c)中的约束。
通过引入辅助变量:

等式(1a)和等式(1c)可变形为
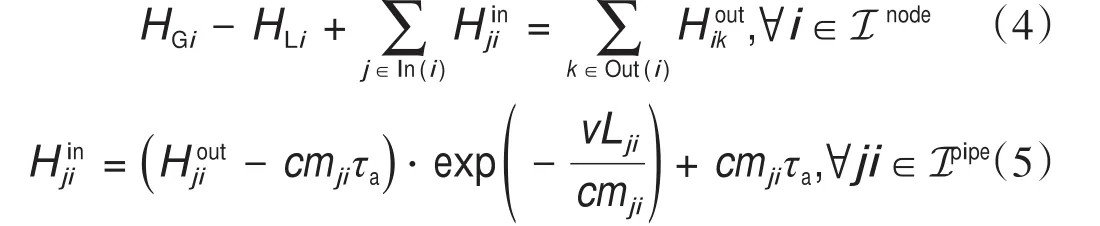
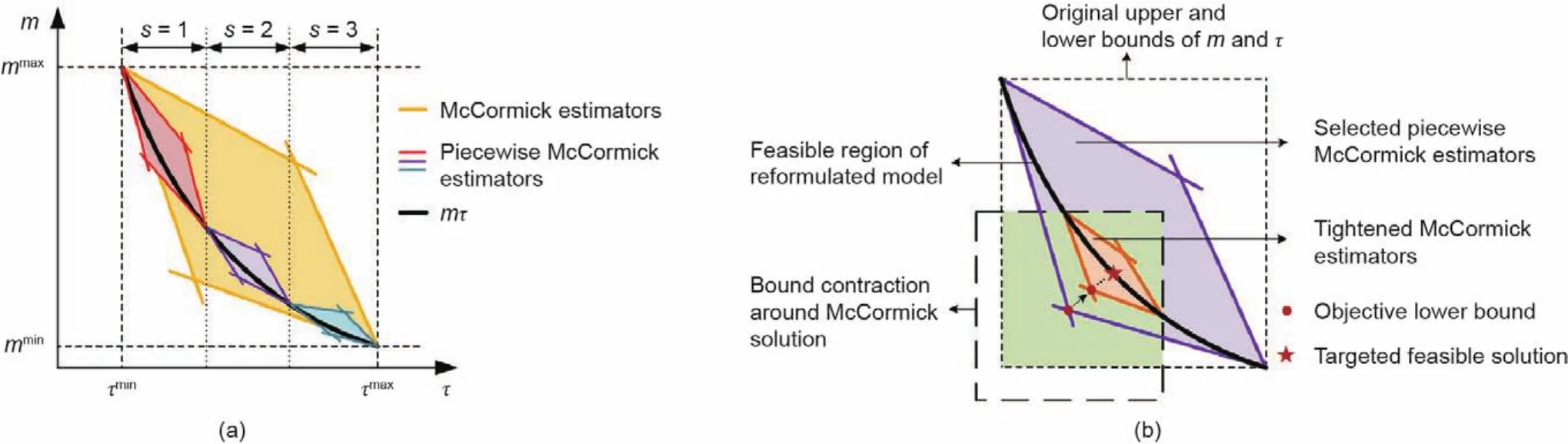
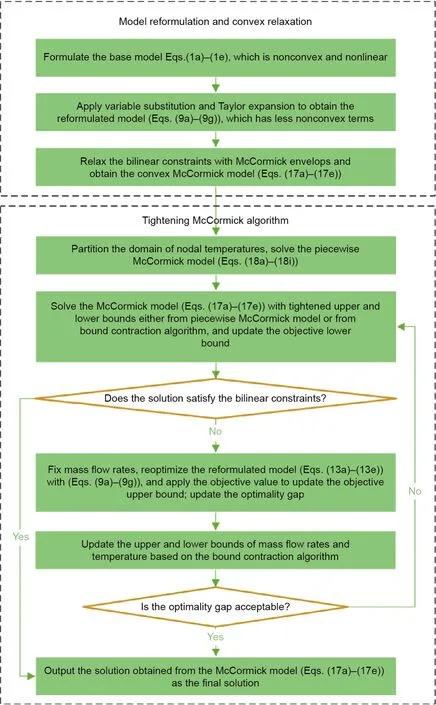
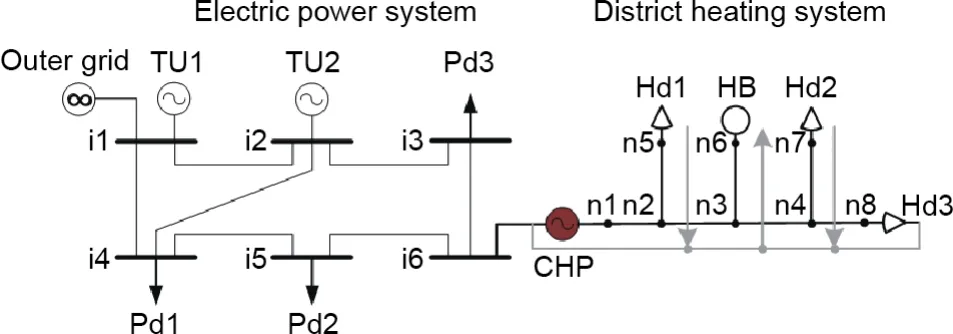
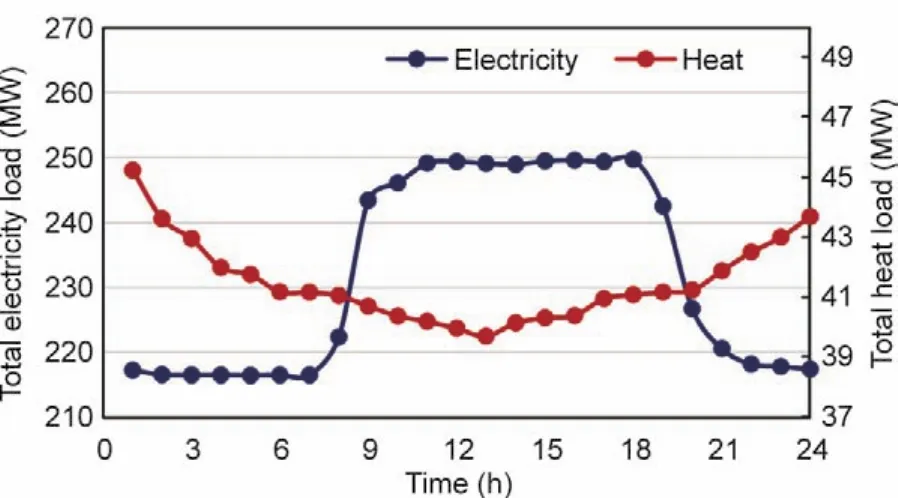
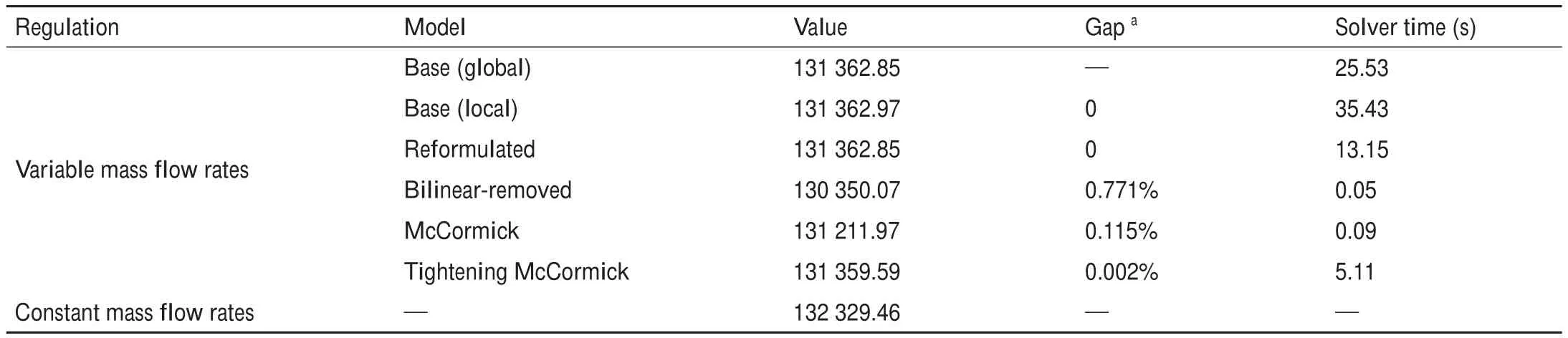
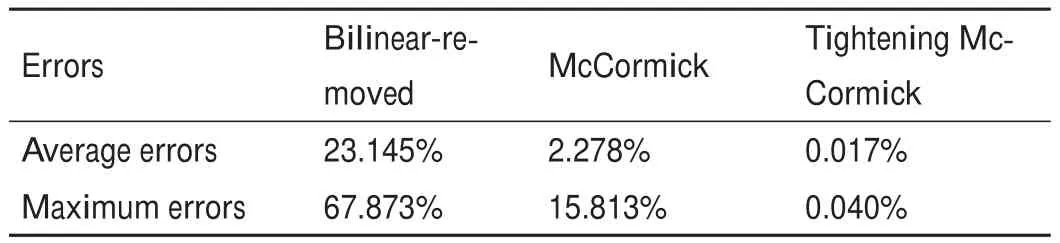
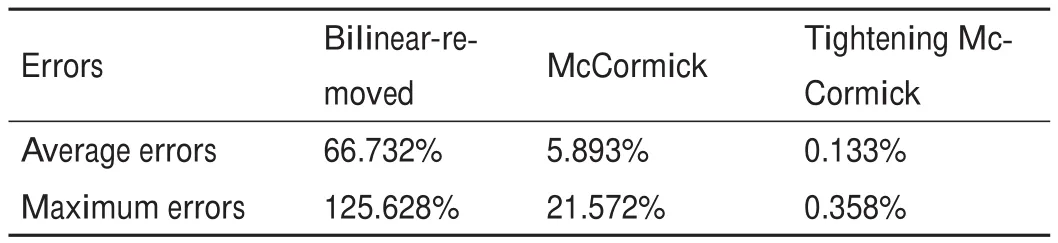
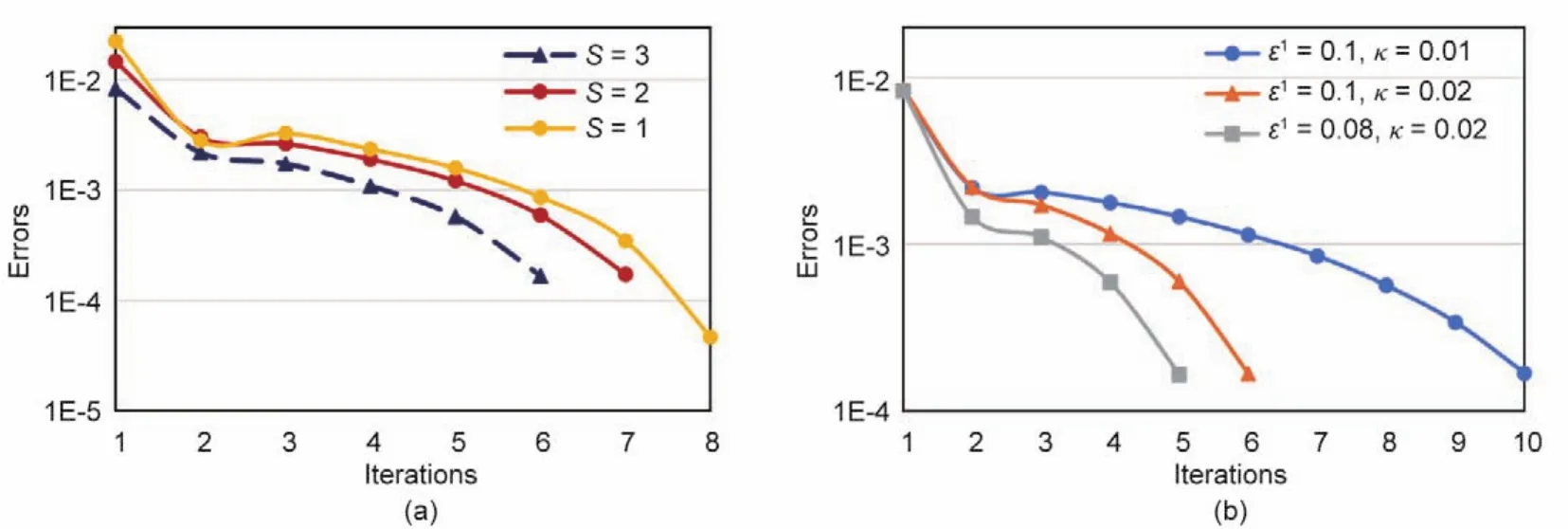
在实际应用中,管道v的总传热系数很小。根据《城镇供热管网设计规范》[23],保温材料的传热系数应小于0.08 W·m-1·K-1。因此,我们假设vLji< 为了将与温度相关的上界和下界约束[即式(1d)]转换为与热功率H相关的约束,我们使用了以下约束: 因此,质量-流量调节下的区域供热网络公式(基础模型)可以重新表述为式(9a)~(9g),也就是重构模型。 重构模型: 需注意的是,等式(2)未出现在重构模型中。它已被消去了,因为可以完全替代τji。引入并消除变量τji[等式(2)]不会影响原问题的可行域。然而,等式(9f)不属于同一情况,因为τi不仅出现在等式(9f)中,也出现在等式(9b)中。在重构模型[式(9g)]中,非凸二次约束[等式(1a)]被转换为线性约束[等式(9a)]和独立的双线性约束[等式(9f)];因此,除了等式(9f)之外,所有约束都是线性的。可以说,重构模型等效于基础模型,一阶泰勒近似的误差可以忽略不计。 本文采用具有精确电压幅值估计的线性潮流模型[24]来表征电力网络;这改善了直流潮流结果,因为它考虑了无功功率和电压幅值。 式中,PGi/QGi是母线i的有功/无功发电量;PLi/QLi是母线i的有功/无功负载;Pij/Qij是线路ij上的有功/无功电流;Vi和θi分别是母线i的电压幅值和相角。gij+jbij是线路ij的导纳,gii+jbii是总线i的并联导纳。是Vi的下界/上界,ij是Pij的上界,Ibus和Iline分别是电力网络中母线和线路的索引集合。等式(10a)和等式(10b)分别定义了节点有功和无功功率平衡方程。等式(10c)和等式(10d)分别表示支路有功和无功功率。式(10e)和式(10f)分别规定了传输线的有功功率限制和总线电压幅值限制。 联合系统中存在三种典型的能源类型:HB、CHP机组和非CHP火电机组。HB的可变成本通常表示为关于热输出的线性函数,一般包括燃料价格和税收价格[25]。CHP机组的发电成本通常表示为电功率和热功率的凸二次成本函数,包括电功率和热功率的乘积项[26]。在MATPOWER[27]中,每个非CHP火电机组的成本可以用二次函数或分段线性函数进行建模,本文选择使用二次函数进行建模。上述能源设备的成本函数描述如下: 以下约束分别为这些能源设备的运行约束。对于CHP机组,运行约束通常是指可行区域的边界,其形状可以是线形或多边形[9],代表热功率和电功率之间的关系以及它们的上下界。 热电联合系统的最优运行问题是使燃料成本、与其他互连电力系统的电力交换成本、网络损耗以及其他一些适当的目标函数最小化。约束包括用于基础模型的式(1a)~(1e)或用于重构模型的式(9g)、式(10)、式(12)以及其他三个关于节点电/热生产的等式约束: 式中,T是运行周期;IFX是电功率交换接口索引集合;是接口j从外网购入的电量;是接口j卖给外网的电量;x代表决策变量。在基础模型中,;在重构模型中,,其中,α、β和γ是权重系数,用于调整不同目标的权重,这是根据系统运行者的偏好设置的。指接口j的电功率交换成本,即从电网购电成本与向电网售电收入之差: 现有文献中包含几种电力网络损耗公式及其变体;有兴趣的读者可以浏览参考文献[28]。在本文中,我们将采用等式(15)这一常见变体,即假设所有电压幅值都等于1(标幺值,p.u.)[29-30]。通常,电压幅值为0.9~1.1 p.u.,所以此假设是合理的。需要注意的是,只要网络损耗公式是凸的,就可以将其应用于本文的联合运行问题。HtLOSS为总的热生产与热需求之差: 无论是使用DHS基础模型[方程(1a)~(1e)]还是重构模型[方程(9a)~(9g)],联合运行问题[方程(13a)~(13e)]都是一个具有二次约束的非凸优化,是非确定性多项式困难问题。 在DHS重构模型中,双线性项是唯一的难点。直观的想法是直接移除等式(9f),以检查双线性约束是否对解的质量有很大的影响。然而,仿真结果表明,去除双线性项会导致解对约束方程(9f)产生很大的违反误差。松弛双线性项的经典方法是使用McCormick包络。为了改善松弛并减少McCormick松弛后的可行域体积,本文提出了分段McCormick技术,分段后产生的较小体积的总和小于标准McCormick方法中的大体积的总和。分段Mc-Cormick技术的最优结果可以看作是松弛后的全局最优,但在重构模型中可能不可行。因此,为了加强McCormick包络的边界,并在松弛的全局最优附近找到可行的结果,本文进一步提出了边界收缩算法。 我们用McCormick松弛替换等式(9f)[31]。 在McCormick松弛下,重构模型成为一个凸问题,其中Karush-Kuhn-Tucker条件是充分必要的(例如,在Slater条件下)。因此,在松弛的McCormick模型中可以得到全局最小值。这个全局最小值可以被视为重构模型的下界。然而,McCormick松弛在双线性约束中仍然会产生相对较大的误差。 我们已经通过凸的McCormick模型得到了一个解。在McCormick模型中,由于松弛的可行域不紧,所得的解可能因违背双线性约束而不可行。为了提高松弛的质量,本文使用更紧的上下界来构建McCormick包络。因此,我们采用分段McCormick技术和边界收缩算法来改进McCormick方法。 3.2.1.分段McCormick技术 在分段McCormick技术中,双线性项中一个变量的域被划分为若干不相交的区域,并确定最优区域,从而收紧所选变量的边界。典型的分区方案是均匀分区[32],其问题大小随分区数量线性增加。其他具有自适应分段长度或分区相关边界设定的分区方案也可以用于此问题以提高性能[33]。 选定需要分区的变量将会影响松弛的质量。在区域供热网络优化问题中,可选择的变量有:质量流量、节点温度或两者的组合。找到可求得最优松弛的最优变量集超出了本文的研究范围。本文将选择对节点温度进行划分。设定τi,smin和τi,smax分别代表分区s中变量τi的下界和上界。将二进制变量yi,s分配给每个分区s。如果τi的值属于分区s,则yi,s=1,否则,yi,s=0。双线性项的另一个变量mik分解为mik,s,s∈S,其中,S是s的索引集合。 在上述公式中,如果二元变量yi,s=1,那么第s个分区中的所有变量,即τi,s和mik,s决定着τi和mik的值。相比之下,所有其他分区中的变量都被强制为零。换言之,如果yi,s=1,则s分区的所有约束条件都将被强制执行,同时所有其他分区中的约束条件都将被忽略。二元变量的数量增加会提升松弛性能,但是也需要解决由此产生的混合整数计算量增加的问题。总体来看,设定分区为3时,该算法运行良好[32]。 3.2.2.边界收缩算法 分段McCormick技术收紧了节点温度上界和下界,从而增强了重构模型的下界解。为了进一步减小双线性约束的违反误差,我们期望可以在下界解附近找到一个可行解。因此,本文提出了一种边界收缩算法来迭代地加强变量边界,并在较少违反双线性约束的情况下逼近最优结果。边界收缩算法的核心思想是:在第n次迭代时,根据n-1次的迭代结果和一系列超参数ε(0<ε<1)去更新决策变量的上界和下界,即质量流量和节点温度。超参数序列的设定原则是逐渐将ε的值减小,以便收紧边界[34]。为了确保原问题的可行性,更新后的边界应该是更新边界和原始边界的交集。当双线性约束[方程(9f)]的平均相对误差达到可接受水平的时候,算法终止。 上述方法的目的是寻找更紧的目标函数下界。然而,我们还需要一个可行解作为目标函数上界,以便对最优间距ω进行评估,也可以作为算法的另一个终止条件。该可行解可以通过以下方案得到:固定从McCormick方法中得到的质量流量或者节点温度,并用固定值重新优化运行问题。 图1直观展示了紧缩McCormick方法,包括分段Mc-Cormick技术和边界收缩算法。图2显示了所提模型和算法的主要流程。经过模型重构和凸松弛,构建了凸的Mc-Cormick模型并得到了一个目标函数下界。为了加强Mc-Cormick松弛性能,对节点温度的可行域进行划分以得到更紧的松弛边界,并用分段McCormick方法求解。同时,可以恢复一个可行解作为目标函数上界,并与目标函数下界一起构成停止条件。可行解可以通过固定质量流量和求解凸的重构模型——式(13a)~(13e)和式(9g)得到。基于边界收缩算法,依次收紧质量流量和节点温度的上、下界。最后,算法收敛到目标函数下界附近的可行的局部最优解。 图1.紧缩McCormick方法的说明。(a)分段McCormick技术;(b)边界收缩算法。 图2.所提模型和方法的实施流程图。 算法1 边界收缩1:2:inputs:δ,ω,ε1,κ,UB=109,LB=0a n←1;mmin,ini ik ←mmin ik,mmax,ini ik ←mmax ik,∀ik∈Ipipe;τmin,ini i ← τmin i ,τmax,ini 3:4:5:6:7:8:9:i ← τmax i ,∀i∈ Inode while(UB-LB)/UB×100%>ωdo if n=1 then Solve(18)and getHout ik,mik,τi,obj;LB←obj else Solve(17)and getHout ik,mik,τi,obj;LB←obj 10:end Fixmik,reoptimize(13)with(9),and obtain a feasible solution and obj;UB←obj if |Ipipe ∑1||Hout ik -cmikτi|/Hout ik ≤ δthen ik∈Ipipe 11:12:13:14:15:break;end mmin ik ← max{(1-εn)mik,mmin,ini ik },∀ik∈ Ipipe mmax ik ← min{(1+εn)mik,mmax,ini ik },∀ik∈Ipipe τmin i ← max{(1-εn)τi,τmin,ini i },∀i∈ Inode i ← min{(1+ εn)τi,τmax,ini i },∀i∈ Inode εn+1 ← εn-κ n←n+1 end while 16:τmax 17:18:19:aUB:upper bound;LB:lower bound. 本节比较了几种模型的性能,如表2所示。 表2 模型对比 本文在两个热电联合系统中测试了这些模型。一个是小规模系统,如图3所示,具有一个6总线的电力系统和一个8节点的区域供热系统。6总线的电力系统在总线1处连接到外部电网。8节点的区域供热系统是根据中国吉林省的一个区域供热系统进行修改的[7]。系统中的设备包括两个非CHP火电机组、三个电力负荷、一个连接电力系统和区域供热系统的CHP机组、一个供暖锅炉和三个热负荷。总的热负荷和电负荷如图4所示。参数设置为ε1=0.02,κ=0.01,δ=0.0001。另一个是大规模系统,由一个改进的118总线电力系统和一个来自巴厘岛的33节点区域供热系统组成[4]。118总线电力系统在69总线处与外部电网交换电力。33节点区域供热系统断开了25~28号支路的连接,形成辐射状网络。系统中有两个CHP机组和一个供暖锅炉。这两个热电联合系统的详细数据见参考文献[35]。 图3.6总线电力系统和8节点区域供热系统的热电联合系统。 图4.总热负荷和电负荷日概况。 表3和表4分别显示了两种案例中的最优调度对比。利用Gurobi9.0中的双线性求解器求解的基础模型和重构模型可以提供全局最优解。这两个模型的最优值几乎没有差别,这表明重构模型可以获得相同的调度方案。正如预期的那样,直接移除双线性项的重构模型提供了目标函数的最小下界解,而McCormick模型提供了更紧的目标函数下界解。由只能获得局部最优解的IPOPT求解的基础模型提供了目标函数上界解。紧缩McCormick模型具有与全局最优值的间隙小、求解快的特质。当网络变大时,用Gurobi中的双线性求解器求解基础模型变得耗时耗力。由于高度非凸,IPOPT在大规模算例中无法收敛。然而,通过对模型进行凸化处理,紧缩McCormick方法可以应用于大规模联合系统优化,求解误差相对较小,并且可以被现成的求解器有效求解。除了分段McCormick技术的求解过程,紧缩McCormick方法中的其他过程实际上都是凸模型。因此,紧缩McCormick方法在求解精度和计算效率方面都表现良好。此外,与Gurobi 9.0中的分支定界等全局搜索方法相比,具有凸性的紧缩McCormick方法可以很容易地推导出影子价格,以便进一步的经济分析。 表3 小规模系统下的最优调度对比 表4 大规模系统下的最优调度对比 从调节方法的角度可以看出,可变质量流量比恒定质量流量的成本更低,如表3和表4所示,这是因为调整质量流量和节点温度可以带来更高的灵活性。图5详细展示了日前调度结果,包括每个生产单元的功率输出、售向电网的功率以及典型管道的质量流量。 图5.小规模系统中不同调节模式的日前调度结果。 图6显示了两个算例系统下违反约束条件[等式(9f)]的情况。用违反双线性约束的误差来表示,即。从表3 和表4 可以看出直接移除双线性项的重构模型和McCormick模型的成本较低,但是二者的约束违反情况也非常严重(图6),不能应用于实际系统运行。但是,紧缩McCormick方法的违反误差相对较小。两个算例系统的最大误差均不超过0.358%,平均误差均小于0.133%。详细的误差数据如表5和表6所示。 图6.第一个时刻处违反约束[方程(9f)]的情况。 表5 小规模情况下双线性约束[方程(9f)]在24 h内的误差 表6 大规模情况下,双线性约束[方程(9f)]在24 h内的误差 从图7(a)可以看出,较大的分区数提供了更紧的上、下界作为边界收缩算法迭代的起点;因此,在第1次迭代中,S=3处的误差是所有分区数中最小的。S=1代表直接使用McCormick模型,不存在分区过程。分区数越大,需要的二元变量越多,计算时间也就越长。当分区数为3或2时,可以获得比较理想的结果。图7(b)表明,初始值越小,步长越大,收敛速度越快。但是,初始值设置不宜过小,步长不宜过大,以防止没有可行域。 图7.小规模系统下的收敛性能。(a)分区数;(b)超参数序列的初始点和步长。S指的是分段McCormick技术中的分区数,ε1和κ分别指超参数序列的初始点和步长。误差显示了双线性约束[方程(9f)]违反情况的平均值。 本文提出了一种凸的热电联合系统的运行模型。为了减少来自热网质量-流量调节的双线性项,本文首先通过变量替换和等效变换对模型进行了重构。接着,本文利用McCormick包络松弛剩余的双线性项。为了进一步缩小McCormick松弛的可行域的体积,本文提出了一种分段McCormick方法来收紧双线性项中决策变量的松弛边界。为了保证结果的可行性,本文提出了一种边界收缩算法来改进McCormick模型的边界,并在附近得到了一个可行解。案例研究表明,紧缩McCormick方法能够快速求解热电联合系统运行问题,得到满足实际运行需求的可行的较优解。此外,紧缩McCormick方法具有凸性,该方法有望用于大规模热电联合系统优化,也可以使用影子价格进行经济分析。值得注意的是,紧缩McCormick方法的性能在很大程度上取决于边界收缩算法中选择的超参数序列。进一步的研究可以以寻找有效的序列和进行灵敏度分析为研究重点。 本文将提出的模型和算法应用于考虑稳态DHS的日前或周前能源生产运行模型。然而,如果考虑传输延迟的热网动态可以表示为凸或双线性约束,则所提方法也可以扩展应用到联合系统的日内或实时经济调度。水质量法已经实现了双线性形式的热网动态模型[15,17]。未来的研究可以着眼于热网动态分析并利用所提方法实现实时经济调度。 致谢 本项工作得到国家电网公司科技项目(522300190008)的支持。 Compliance with ethics guidelines Lirong Deng,Hongbin Sun,Baoju Li,Yong Sun,Tianshu Yang,and Xuan Zhang declare that they have no conflict of interest or financial conflicts to disclose.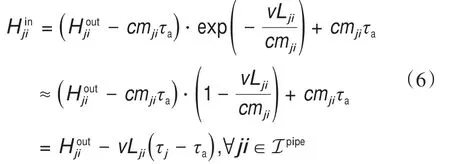
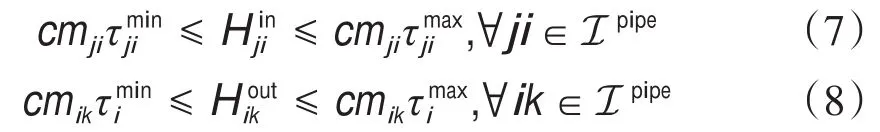
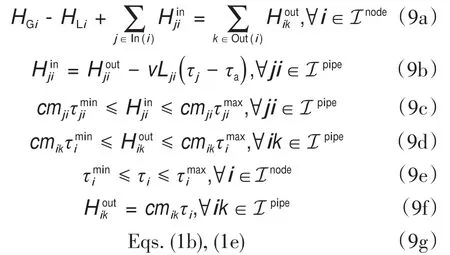
2.3.电力系统建模
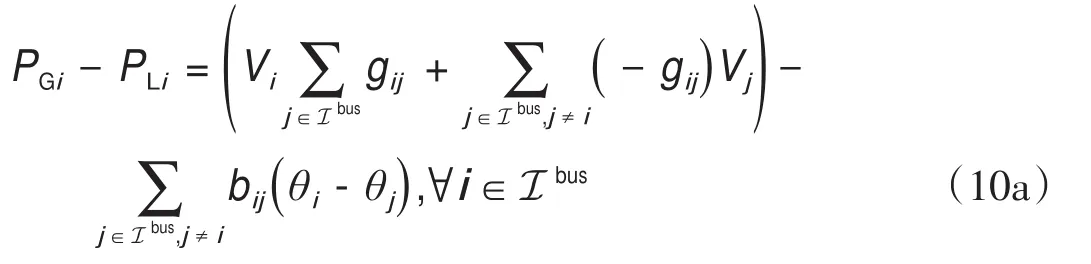
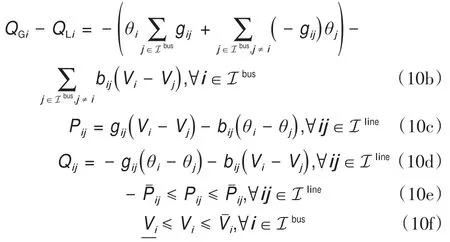
2.4.能源设备建模
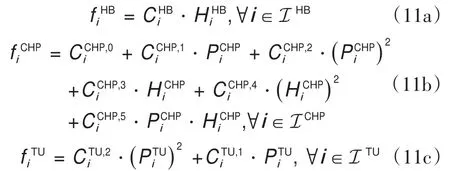
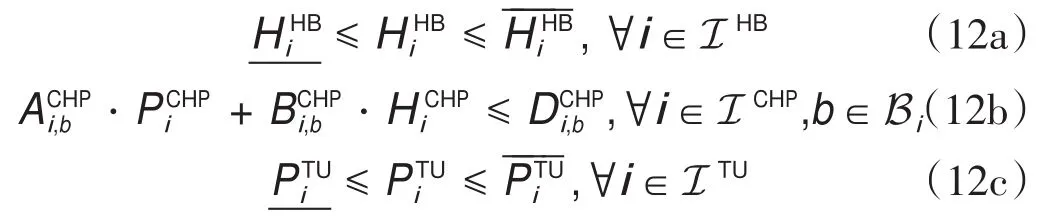
2.5.运行问题
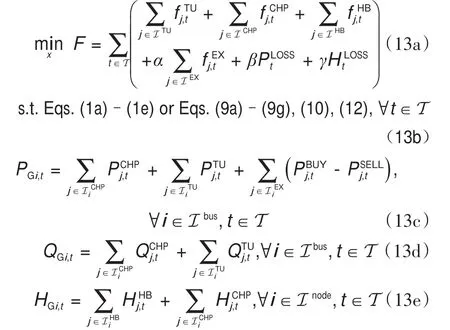

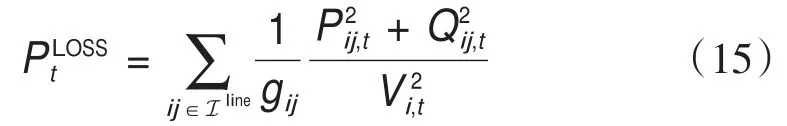

3.凸松弛及求解算法
3.1.McCormick凸松弛
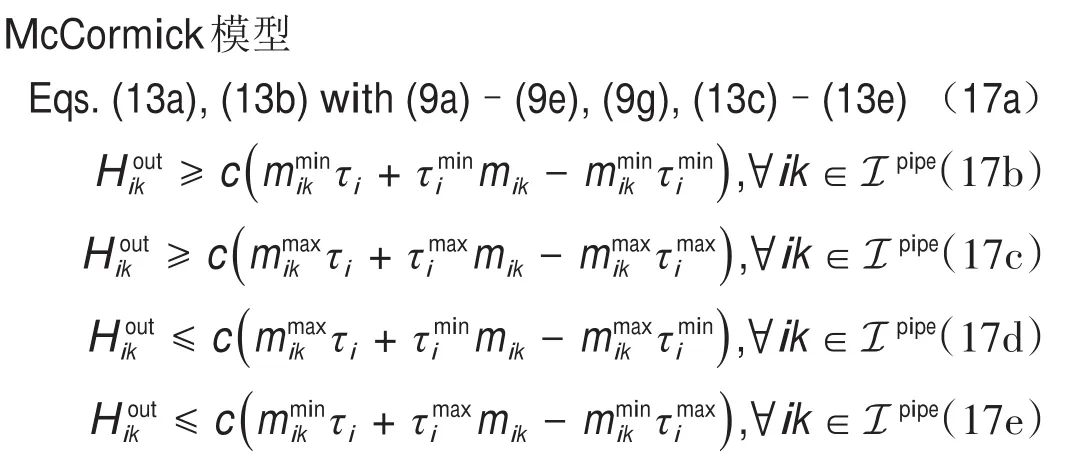
3.2.紧缩McCormick方法

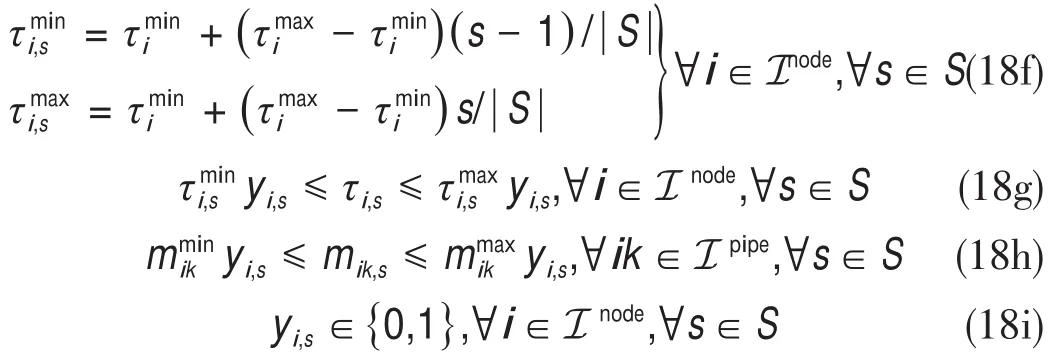
3.3.所提模型和方法的总览

4.算例研究
4.1.最优性
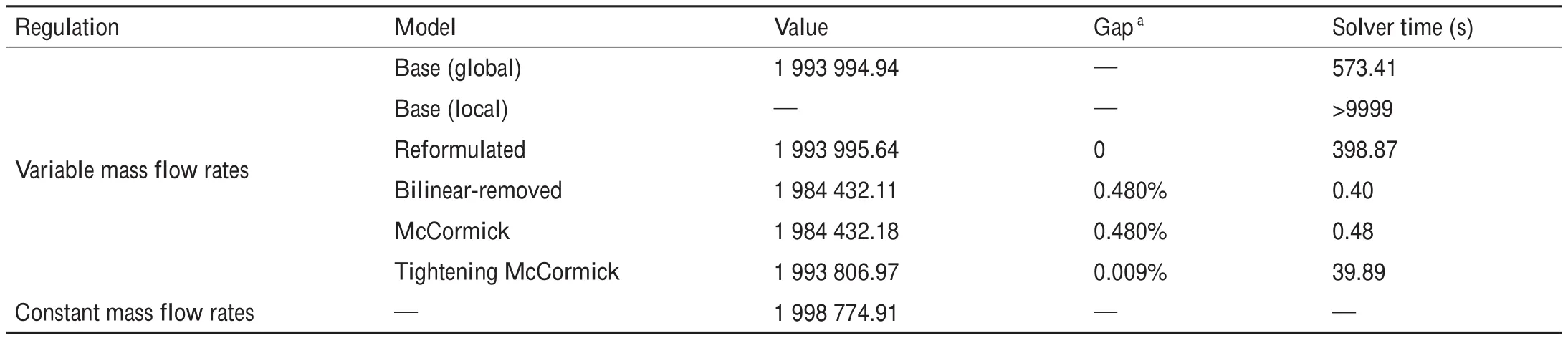
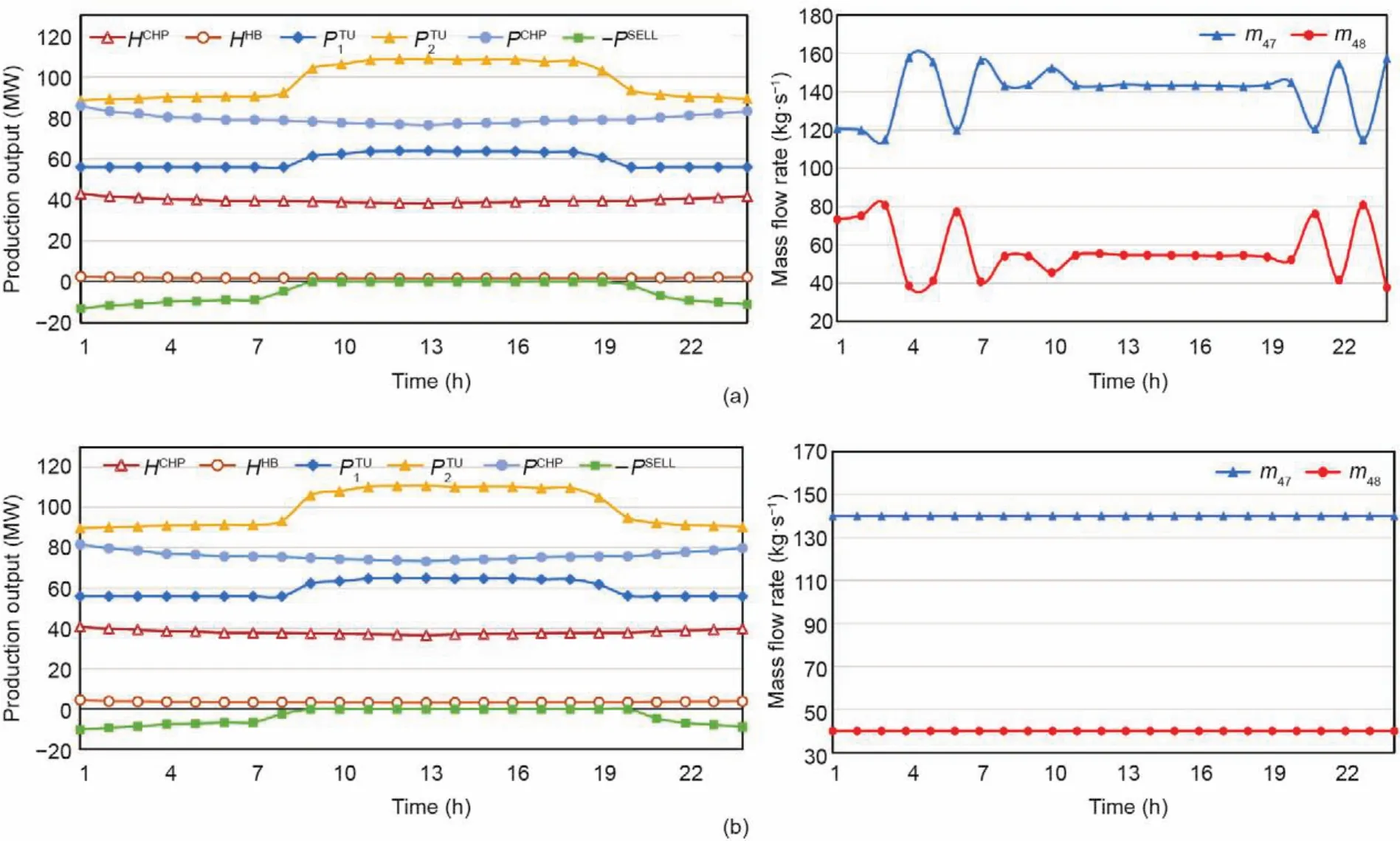
4.2.可行性
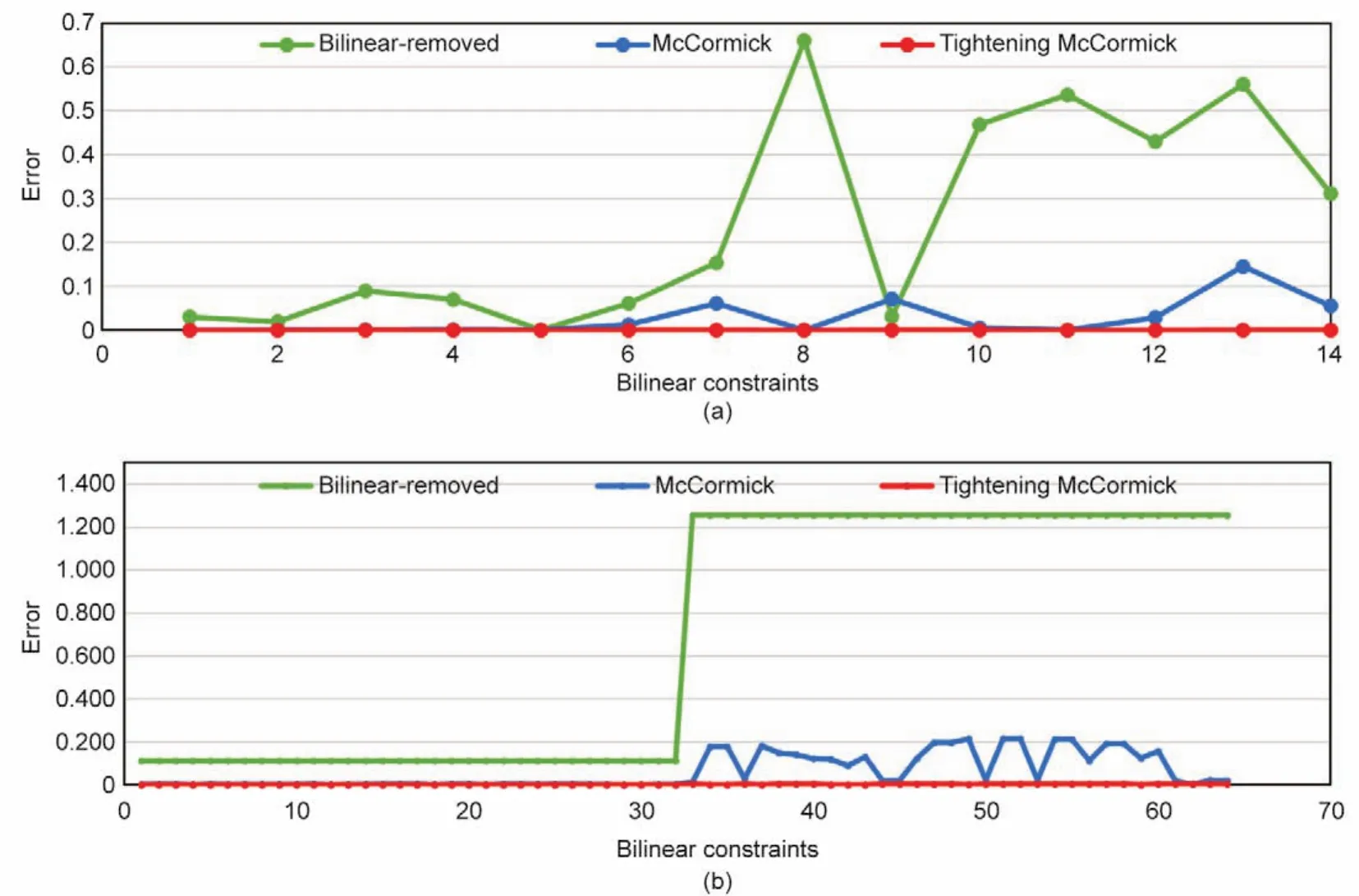
4.3.灵敏度分析
5.结论
