心电信号去噪效果的评估与分析
2022-01-22杨承金聂春燕车敏诗阮新磊范如俊
杨承金,聂春燕,车敏诗,阮新磊,范如俊
1.长春大学电子信息工程学院,长春 130022
2.杭叉集团股份有限公司研发部,杭州 311305
心电信号是临床医学中最常用的生物电信号,它记录了每一次心动周期产生的电位变化,每个正常的心动周期根据时间的先后顺序依次由P 波、QRS 波群、ST段、T波构成[1],这些特征参数的准确性对诊断心脏的健康状况具有重要的意义。心电信号的幅值为毫伏级,在采集过程中易受到人体呼吸、肌肉抖动和设备电路的影响,从而产生基线漂移、肌电干扰和工频干扰[2-4],这些干扰会对心电信号的特征参数造成破坏,使心脏诊断无法正常进行,甚至造成严重的医疗事故。因此,心电信号的去噪技术一直是学者们研究的热点,
近年来,随着信号处理技术的快速发展,对心电信号的去噪方法逐渐走向成熟,根据3种噪声(基线漂移、肌电干扰和工频干扰)频率分布不同的特点,每种噪声主要采用单独的算法进行去噪处理,目前,常用来处理基线漂移的算法有:小波变换法、中值滤波法和形态学滤波法,常用来处理工频干扰的算法有:陷波滤波法、平滑滤波法和自适应滤波法,常用来处理肌电干扰的算法有:小波阈值法、经验模态分解法和低通滤波法,其中,小波变换法具有多分辨分析的特点,可以对信号的任意细节进行多尺度的时频域分析,对滤除频带与心电信号频率范围相互分离的基线漂移较为有效[5-6]。中值滤波法可以对信号中出现的短暂脉冲值即噪声点进行抑制,将噪声点用该点邻域的中值代替,对心电信号中非高斯噪声的去噪效果较好[7]。形态学滤波法是一种常用来处理非线性信号的去噪方法,具有保护信号几何特征的特点[8]。陷波滤波法通过将信号某一频率上的值迅速衰减,从而抑制了固定频率为50 Hz 的工频干扰[9]。平滑滤波法具有减弱信号中的高频分量,但不影响低频分量的特点,对50 Hz 的工频干扰较为有效[10]。自适应滤波法常被用来处理生物体内的非平稳信号,对心电信号的去噪效果较好[11-12]。小波阈值法是在小波变化法的基础上,对含噪声的小波分量进行阈值处理,可以有效地解决心电信号与肌电噪声频率叠加的情况[13]。经验模态分解法可以对数据局部信息进行平稳化处理,适用于去除频率分布较广的肌电干扰[14-15]。低通滤波法具有算法简单,处理时间短等特点,可以对心电信号中高频部分的肌电干扰进行快速处理[16]。
通过深入了解国内外心电信号的去噪研究成果后发现:虽然目前对含单一噪声的心电信号研究成果较多,但并没有统一的标准对这些算法的去噪效果进行比较和评估。同时,在实际情况中心电信号往往存在多种噪声,由于3 种噪声的频率分布不同,目前含多噪声的心电信号去噪方法主要采用上述去噪算法对其进行分步去噪[17],但这些去噪算法对含有多噪声的心电信号的去噪效果无统一结论,因此有待进一步考证。本文首先分析了3种噪声(基线漂移、工频干扰和肌电干扰)在心电信号频谱图中的干扰特点,模拟出理想情况下的纯净心电信号,在添加噪声后对上述9 种去噪算法进行仿真,通过计算信噪比和均方差两种参数以及对比去噪前后心电信号特征值和频谱图的实际变化来对心电信号的去噪效果进行评估。最后,选择去噪效果较好的算法对含有多噪声的心电信号进行去噪及分析。
1 含噪心电信号的频域分析
心电信号是一种最大幅值不超过5 mV、频率范围在0.05~100 Hz 之间的低频生物电信号[18],在采集过程中极易受各种噪声的干扰,这些干扰包括:基线漂移、工频干扰、肌电干扰、运动伪迹、机器故障和外界环境因素干扰[19],其中,运动伪迹可以通过减少身体的晃动和加固电极贴片来有效的避免,机器故障和外界环境因素干扰可以通过对采集设备进行故障排查并选择安静适宜的实验环境来消除噪声源。而基线漂移、肌电干扰的干扰源来主要自身体内部,工频干扰由电路受到电磁反应而产生,它们在心电信号采集过程中不易被避免,因此,在研究心电信号去噪算法时,主要选择基线漂移、肌电干扰和工频干扰作为心电信号去噪的研究对象。
1.1 含基线漂移的心电信号频域分析
基线漂移是采集心电信号时由呼吸引发的肌肉轻微颤动所造成的微弱低频干扰[20],基线漂移的存在会对心电特征中的S-T 段斜率以及R-R 间距的判断产生影响,基线漂移的噪声频率通常在0.05~2 Hz 之间,低于P波、QRS 波群和T 波的主要频率分布范围,在频谱图中表现为:正常心电信号低于2 Hz的低频分量幅值较低,含有基线漂移的心电信号低频分量幅值较大。含基线漂移干扰的频谱图如图1所示。

图1 含基线漂移干扰的心电信号频谱图Fig.1 Spectrum of ECG with baseline drift
1.2 含工频干扰的心电信号频谱分析
工频干扰主要是在心电信号采集过程中由于采集设备中的交流电流不稳定引起电路产生电磁反应造成[21],工频干扰的特点是频率固定为50 Hz 或60 Hz,其噪声成分主要为正弦波,在频谱图中表现为50 Hz 或60 Hz处出现一个幅值较高的峰值,且幅值较大,最高可达到心电信号幅值的50%,工频干扰会对心电信号整体特征造成影响,含工频干扰的频谱图如图2所示。

图2 含工频干扰的心电信号频谱图Fig.2 Spectrum of ECG with power frequency interference
1.3 含肌电干扰的心电信号频谱分析
肌电干扰是心电信号在采集过程中由贴片电极受到肌肉刺激引起的高频干扰[22],振幅一般不超过1 mV,但其频率变化范围较广,在5 Hz 到2 000 Hz 之间,类似零均值的高斯白噪声,在心电信号频谱图中与P 波、QRS波群和T波造成幅值的叠加,使正常的心电信号频谱波形被“淹没”,通常根据心电信号在频率45 Hz之后的能量分布较小的特点,作为判断肌电干扰强度的依据。含肌电干扰的频谱图如图3所示。

图3 含肌电干扰的心电信号频谱图Fig.3 Spectrum of ECG with myoelectric interference
2 去噪效果的评估标准
文中选取信噪比(SNR)和均方差(MSE)作为比较心电信号去噪效果的客观评价标准,定义分别如公式(1)和公式(2)所示:

其中,y(n)表示纯净的心电信号,x(n)表示经过去噪处理后的心电信号,N表示心电信号的采样点数。由以上两式可知,SNR 越大、MSE 越小说明去噪效果较好,反之,则说明去噪效果较差。
除计算信噪比和均方差两种参数外,本文还选择比较P波、QRS波群、T波、S-T段、R-R间距和P-R间距6种心电特征值以及噪声频率的幅度变化情况来作为去噪效果的直观评价标准。
3 实验数据的来源
近年来,模拟心电信号技术发展已较为成熟,在临床医学领域中发挥了及其重要的作用,模拟心电信号与实际心电信号相比,具有获取方法简单,噪声干扰低和模拟心电种类齐全等特点。目前,模拟心电信号主要用在心电设备的定标与评测、各种病理心电信号的研究、标准数据库的建立以及心电知识教学中[23]。研究表明,心电信号自身满足周期性和狄利克雷条件,因此可以用傅立叶级数来模拟心电信号,其中,QRS 波群可以用三角波表示,P波、T波可以用正弦波表示[24]。
实际采集到的心电信号难以保证干净无噪声,不能满足信噪比和均方差的计算条件,为了获得纯净的心电信号,文中采用模拟的理想心电信号作为实验数据。
分别计算模拟出心电特征值为0.23 mV 的P 波、0.35 mV 的T 波、0.04 mV 的U 波和1.57 mV 的R 波,且其R-R间隔和P-R间隔分别0.827 s和0.041 s,经过叠加得到理想状态下采样频率为360 Hz、采样时间为6 s 的理想心电信号。向理想心电信号中分别填加0.15 Hz正弦信号、50 Hz 正弦信号和高斯白噪声来模拟受基线漂移、工频干扰和肌电干扰的心电信号,其频谱图如图4所示。

图4 含3种模拟噪声的心电信号频谱图Fig.4 Spectrum of ECG with 3 kinds of analog noise
4 心电信号去噪效果的评估
通过对心电噪声的频域分析得知,基线漂移、工频干扰和肌电干扰的频率分布不同,根据这一特点,可以针对每种心电噪声进行单独去噪。本文采用模拟理想状态下的心电信号并添加轻微和严重两种强度下的3种模拟噪声进行仿真,通过比较去噪前后心电信号的特征值、频谱图变化情况以及计算信噪比和均方差两种参数进行去噪效果的评价。
4.1 去除基线漂移噪声的方法及效果分析
本文选择小波变化法、中值滤波法和形态学滤波法对基线漂移进行去噪效果的比较,并将去噪结果记录在表1、表2和表3中。
小波变换法是一种对信号的局部特征同时进行时频域分析的方法,具有多分辨率分析的特点,小波变换法去除基线漂移的原理是:首先选择小波基对信号进行多尺度的分解,得到每一层的低频近似分量和高频细节分量,小波分解示意图如图5 所示,然后去除基线漂移噪声所在频率的分量,最后进行小波重构,从而获得去噪后的心电信号。本文选择coif3小波对含基线漂移的心电信号进行小波分解,分解效果如图6所示。

图5 小波分解示意图Fig.5 Wavelet decomposition diagram
从图6 中可以得出,当对含噪心电信号分解到第9层时,其频率分量与基线漂移的噪声频率比较接近,因此去掉第9层频率分量并对信号进行小波重构,获得去噪后的心电信号,去噪评估参数如表1 所示,经实验仿真后的频谱图如图7(a)、(b)所示。

图6 含基线漂移心电信号的小波分解Fig.6 Wavelet decomposition of ECG with baseline drift
通过表1 获知,对于轻微和严重情况下基线漂移干扰,经小波变换去噪后的心电信号特征值与理想心电信号差别不大,心电信号特征保留较完整,通过图7(a)、(b)获知,去噪后心电信号的低频分量得到很好的抑制,并且对其他频率分量没有造成影响,总体效果很好。

图7 小波变换法去噪结果Fig.7 Wavelet transform denoising results

表1 小波变换法去除基线漂移Table 1 Wavelet transform removes baseline drift
中值滤波法是一种非线性滤波算法,具有保护数据边缘和抑制噪声等特点,其滤波原理是把心电信号某一点的值,用该点邻域内各点的中值代替,从而得到运动变化较缓慢的基线漂移数据,再把含噪心电信号与基线漂移数据相叠加,从而获得去噪后的心电信号,中值滤波原理可以用式(3)表示。
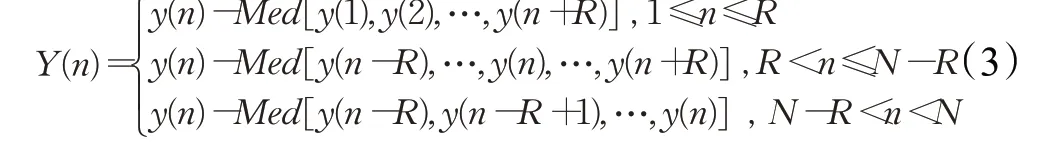
其中Y(n)表示去噪后的心电信号,y(n)表示含基线漂移的心电信号,Med[]表示取中括号中元素的中值,N表示心电信号的采样点数,R的取值与邻域的宽度l有关,l=2R+1=0.3fs,将N=3 600,fs=360代入式(3)可以得到经中值滤波去噪后的心电信号,去噪评估参数如表2 所示,经实验仿真后的频谱图如图8(a)、(b)所示。
通过图8(a)、(b)获知,中值滤波法对2 Hz 以下的基线漂移干扰具有一定的抑制作用,其中,对轻微的基线漂移干扰抑制效果较好,但对5 Hz 以下频率分量有轻微干扰,对严重的基线漂移抑制效果一般,且对10 Hz以下频率分量有明显干扰,10 Hz 以下属于T 波的频率分布范围,因此去噪后造成T波失真。由表2获知,对不同干扰强度的基线漂移去噪后,造成T 波不同程度“削峰”,同时造成心电信号S-T段的斜率发生轻微改变。

表2 中值滤波法去除基线漂移Table 2 Median filtering removes baseline drift
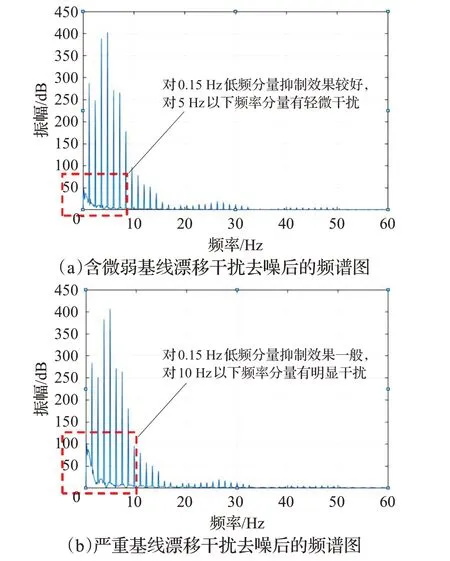
图8 中值滤波法去噪结果Fig.8 Median filtering denoising results
形态学滤波也是一种常用的非线性滤波算法,它的主要特点是可以很好的保护信号的几何特征,因此常被用来对心电信号进行去噪分析。它的去噪原理是首先选择一种结构元素作为在心电信号间游走“探针”,并不断的对心电信号进行腐蚀与膨胀运算,腐蚀与膨胀的运算公式分别如公式(4)和公式(5)所示:
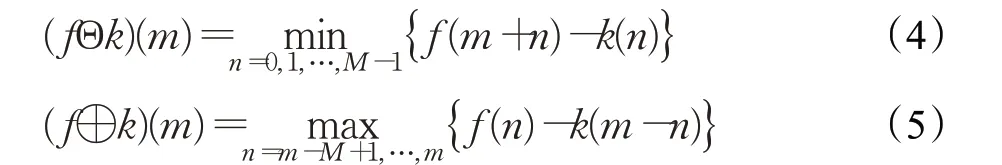
其中,M表示采样点数,f(m)表示含基线漂移干扰的心电信号,先腐蚀再膨胀称为开运算,先膨胀再腐蚀称为闭运算,当进行开运算时结构元素游走在心电信号上方,削除信号突出的“波峰”,使信号更光滑。当进行闭运算时结构元素游走在心电信号下方,填充信号多余的“波谷”,同样使信号更光滑,通过一系列的开闭运算,即可得到经形态学滤波后的心电信号,去噪评估参数如表3所示,仿真结果如图9(a)、(b)所示。

表3 形态学滤波法去除基线漂移Table 3 Morphological filtering removes baseline drift

图9 形态学滤波去噪结果Fig.9 Morphological filtering denoising results
通过9(a)、(b)可以发现,当基线漂移干扰比较小时,形态学滤波对低频分量的抑制效果较好,当基线漂移干扰较严重时,形态学滤波对低频分量的抑制效果较差,基线漂移滤除不彻底。通过表3 可以发现,当基线漂移干扰比较微弱时,去噪后的心电信号与理想心电信号的时域特征值相差不大,效果较好。当基线漂移干扰较严重时,由于基线滤除不彻底,使T 波末端到P 波起始端的基线被拉低,造成P 波与T 波峰值略高于实际值。
通过表1~3可以获知,信噪比和均方差可以准确的反应出实际的去噪效果,经小波变换法去噪后的心电特征值与理想心电信号较接近,信噪比最高,均方差最低,去噪效果最好。形态学滤波法对微弱基线漂移干扰的去噪效果较好,去噪后与理想心电信号较接近,当基线漂移干扰较严重时,对基线漂移滤除不彻底,造成P 波与T波的峰值略高于实际值,与小波变换法相比信噪比略低,均方差略高。中值滤波法去噪后的心电信号Q波、T 波和QRS 波群的特征保留较好,但S-T 段产生比较明显的下移,与上述两种方法相比,信噪比较低、均方差较高。
4.2 去除工频干扰噪声的方法及效果分析
本文选择陷波滤波法、平滑滤波法和自适应滤波法对工频干扰进行去噪效果的比较,并将去噪结果记录在表4~6中。
陷波滤波器属于带阻滤波器的一种,它的特点是其阻带非常短,因此使输入信号某一频率的分量迅速衰减,阻碍心电信号中包含的固定50 Hz频率的工频干扰通过阻带,从而达到滤波的目的。本文通过对巴特沃斯低通滤波器进行双线性变换得到数字陷波器,它的变换过程如公式(6)所示:
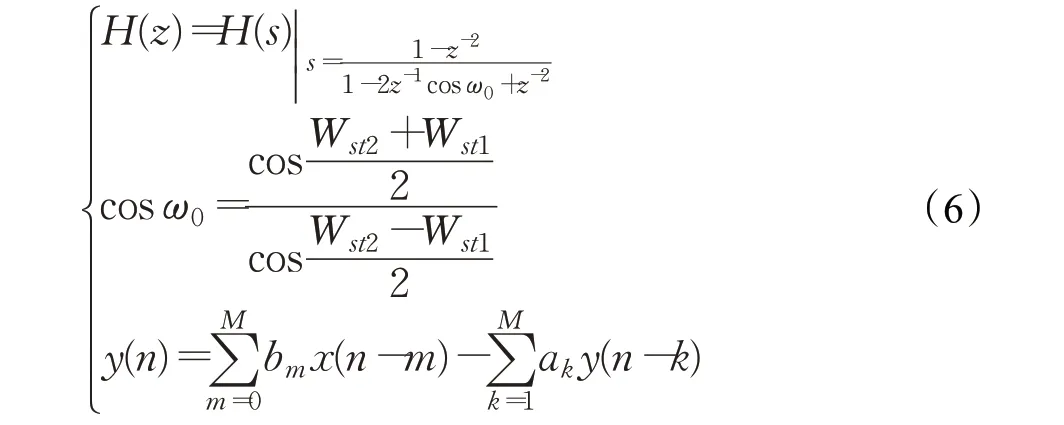
其中,H(s)表示含噪心电信号复频域的系统函数,Wst1和Wst2分别表示巴特沃斯低通滤波器的下通带截止频率和上通带截止频率,ak和bm分别表示系统函数H(z)的分母系数和分子系数,x(n)和y(n)分别表示去噪前和去噪后的心电信号。经实验仿真后的心电信号去噪评估参数如表4所示,频谱图如图10(a)、(b)所示。

表4 陷波滤波法去除工频干扰Table 4 Notch filter removes power frequency interference
通过图10(a)、(b)可以发现,陷波滤波法对含轻微和严重工频干扰的心电信号滤除效果较好,去噪后心电信号中的50 Hz工频干扰被完全滤除,且对其他频率分量没有产生影响,通过表4 可以发现,去噪后的心电信号特征值与理想心电信号一致,信噪比较高,同时均方差较低。

图10 陷波滤波法去噪结果Fig.10 Notch filter denoising results
平滑滤波法是一种增强低频、抑制高频的滤波方法,由于心电信号的主要频率分布在0.05~45 Hz 之间,50 Hz 的工频干扰相对于心电信号属于高频干扰,因此可以用平滑滤波法进行滤除。本文采用平滑滤波法中的五点三次滤波法进行去噪,其去噪原理是对心电信号每个数据点取相邻的且包含该点的5个数据点,通过最小二乘法拟合出一条3 次曲线,然后选择3 次曲线上相应位置的数据值作为滤波后的结果。该方法的优点是可以保护峰值,而且对心电信号的边缘数据去噪效果较好,它的去噪过程如公式(7)所示:
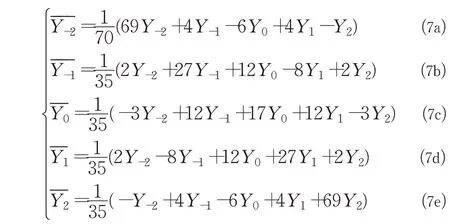
其中,Y0表示心电数据点,Y-1、Y-2、Y1、Y2分别表示Y0左右邻域内相邻的4个数据点,Yˉ表示去噪后的数据点,公式(7a)、(7b)用来处理数据左端的数据点,公式(7d)、(7e)用来处理数据右端的数据点,其余数据点全部用公式(7c)来处理。经实验仿真后的心电信号去噪评估参数如表5所示,频谱图如图11(a)、(b)所示。

表5 平滑滤波法去除工频干扰Table 5 Smooth filtering removes power frequency interference
通过图11(a)、(b)可以发现,平滑滤波对50 Hz 工频干扰滤除效果较好,滤除效果比较彻底,但同时也滤除了40~50 Hz内的有用心电信号,该频率段内属于R波的频率分布范围,因此会对R 波造成微弱影响,随着工频干扰程度的增加,平滑滤波的影响范围会逐渐向低频分量蔓延,吞没有用心电信号。通过表5 可以发现,经平滑滤波去噪后,对R峰存在0.1 mV左右的微弱削峰,其余特征值与理想心电信号一致。

图11 平滑滤波法去噪结果Fig.11 Smooth filtering denoising results
自适应滤波法是一种对非平稳信号进行去噪的算法,因此常被用来对心电信号进行去噪研究,它可以通过前一时刻滤波器的输出结果来自动调节现时刻的滤波器参数,从而达到滤波的目的,本文采用较为常用的LMS 算法作为本实验的自适应滤波算法,它的滤波过程如图12所示。
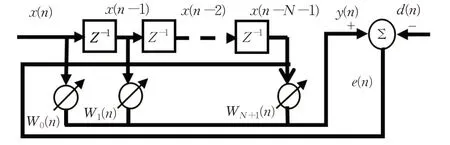
图12 LMS自适应滤波Fig.12 LMS adaptive filtering
在图12中,x(n)为含噪心电信号,通过可调节系数W(n)的滤波器后输出去噪后的信号y(n),将输出信号y(n) 与理想心电信号d(n) 进行对比,得到误差信号e(n),如果e(n)没有达到预期要求,则将e(n)反馈到滤波器中,滤波器自动调整系数W(n)进行下一次滤波,从而达到自动滤波的目的。滤波算法如公式(8)所示:
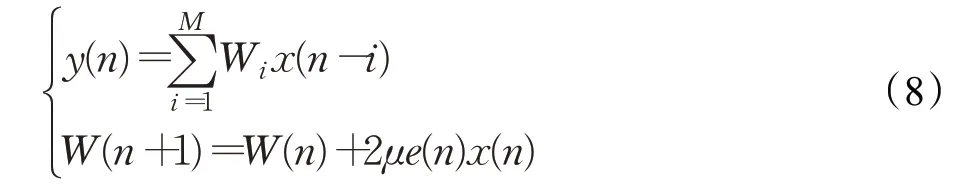
其中,M表示心电信号采样点数,μ表示步长,即滤波前后时刻的时间间隔。经实验仿真后的心电信号去噪评估参数如表6所示,频谱图如图13(a)、(b)所示。
通过图13(a)、(b)可以发现,当工频干扰较微弱时,自适应滤波对50 Hz 工频干扰滤除较彻底,但是会对0~15 Hz 范围内的心电信号造成微弱影响,当工频干扰较严重时,自适应滤波对50 Hz 工频干扰滤除不彻底,同时对0~15 Hz 范围内的心电信号影响较为严重,0~15 Hz 属于心电信号P 波的主要频率分布范围,因此去噪后会对P 波造成失真。通过表6 可以发现,自适应滤波对微弱工频干扰的去噪效果较好,P 波失真较小,当工频干扰较严重时,去噪后心电信号中存在0.1 mV 的工频噪声残留,且对P 波造成0.3 mV 左右的削峰。

图13 自适应滤波法去噪结果Fig.13 Adaptive filtering denoising results

表6 自适应滤波法去工频干扰Table 6 Adaptive filtering removes power frequency interference
通过表4~6可以获知,经陷波滤波法去噪后的心电信号信噪比最高,均方差最低,去噪效果最好。平滑滤波法对工频干扰的滤除比较彻底,但随着工频干扰程度的加重,去噪后会对心电信号造成一定影响,信噪比略低于陷波滤波法。自适应滤波法对微弱的工频干扰去噪较彻底,对严重的工频干扰去噪不彻底,且对P 波造成一定程度的失真,与上述两种方法相比,信噪比较低、均方差较高。
4.3 去除肌电干扰噪声的方法及效果分析
本文选择小波阈值法、经验模态分解法和低通滤波法对工频干扰进行去噪效果的比较,并将去噪结果记录在表7~9中。
小波阈值法是基于小波变换的对信号进行去噪的方法,它可以对小波分解的系数设置阈值,由于心电信号在时间域上是连续的,因此在小波域,有效信号所产生的小波系数其模值往往较大,而肌电干扰的特性类似于高斯白噪声,在时间域上并不连续,因此噪声所产生的小波系数其模值较小,根据这一特点,只要对小波分解后的系数设置阈值,即可以把心电信号和噪声分离开来。对心电信号进行小波阈值去噪主要有三步:小波分解、阈值处理和小波重构,其中小波分解和小波重构在4.1 节已经介绍完毕,阈值处理主要包括两个内容,即:确定阈值和选择阈值函数,本文选择无偏风险法确定阈值,如公式(9)所示,并选择软阈值作为阈值函数,如公式(10)所示:

其中,λ表示阈值,f(k)表示将原信号中的元素从小到大排列后的平方函数,Risk(k)表示阈值产生风险系数,kmin表示风险系数最小时k的值。

其中,w表示小波分解系数,wλ表示经阈值处理后的小波分解系数,经实验仿真后的心电信号去噪评估参数如表7所示,频谱图如图14(a)、(b)所示。
通过图14(a)、(b)可以发现,用小波阈值法对心电信号进行去噪,对有用信号频率影响较小。通过表7可以发现,去噪后的心电信号特征值与理想心电信号较为接近,心电信号失真较小。

图14 小波阈值法去噪结果Fig.14 Wavelet threshold denoising results

表7 小波阈值法去肌电干扰Table 7 Wavelet threshold removes myoelectric interference
经验模态分解法(EMD)同样是对信号的时频域进行分析和处理的方法,与小波变换相比,它具有克服无基函数无法自动适应的特点。EMD的分解过程是简单直观的,主要通过对原信号进行不断迭代而获得内涵模态分量(IMF),将原信号分解成若干个内涵模态分量和一个剩余残量叠加的形式,之后对噪声所在的分量进行处理,最后再对分量进行叠加从而达到去噪的目的,它的去噪示意图如图15所示。
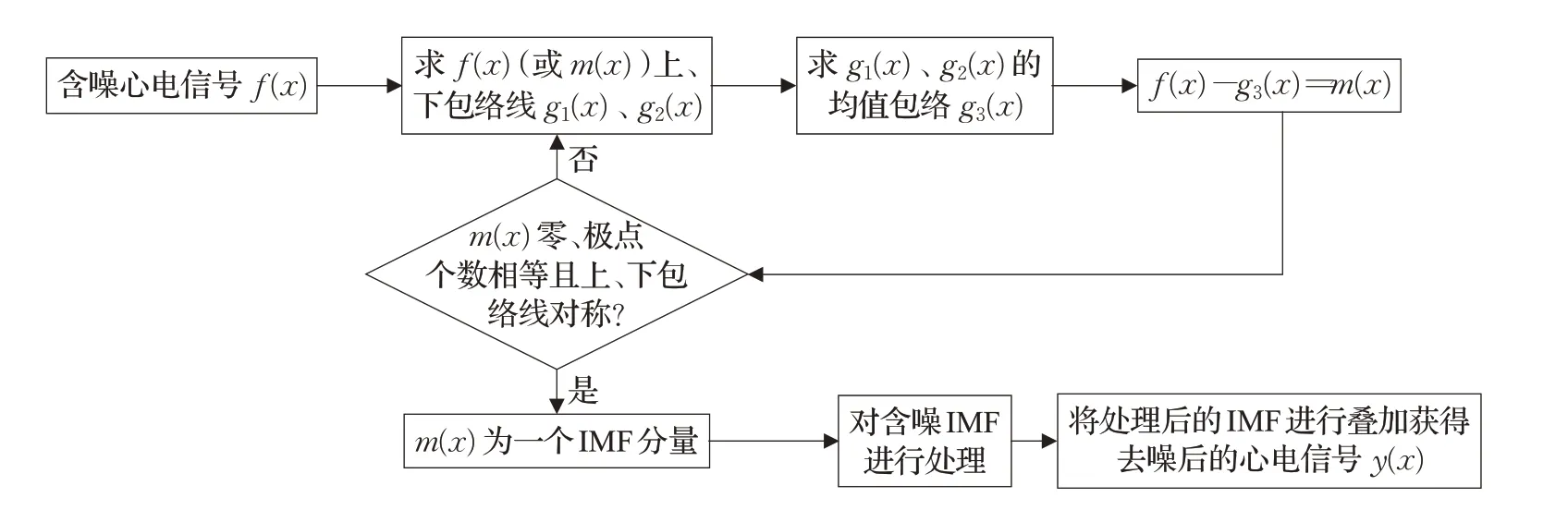
图15 经验模态分解法去噪示意图Fig.15 Schematic diagram of EMD denoising
本文将含噪心电信号进行EMD 分解得到9 层IMF分量,如图16所示。

图16 含噪心电信号经验模态分解Fig.16 EMD of noisy ECG signals
分别计算每层IMF 的赫斯特指数,得到IMF1、IMF2 和IMF3 的赫斯特指数小于0.5,因此肌电干扰主要存在前3 层IMF 分量中,由于前3 层IMF 分量的频率分布大于心电信号的频率分布,因此剔除前3 层IMF分量,将剩余的分量进行重构得到去噪后的心电信号,去噪后的评估参数如表8 所示,频谱图如图17(a)、(b)所示。

表8 经验模态分解法去肌电干扰Table 8 EMD removes myoelectric interference
通过图17(a)、(b)可以发现,经验模态分解法对含微弱肌电干扰的心电信号的主要频率保护较好,但20 Hz之后的心电信号成分被滤除,造成一定失真,当肌电干扰较严重时,心电信号的主要频率成分也被破坏,对心电信号整体造成失真。通过表8可以发现,当干扰程度较微弱时,去噪后的心电信号特征值与理想信号差距不大,当干扰程度较严重时,心电信号特征值变化较大,造成一定失真。
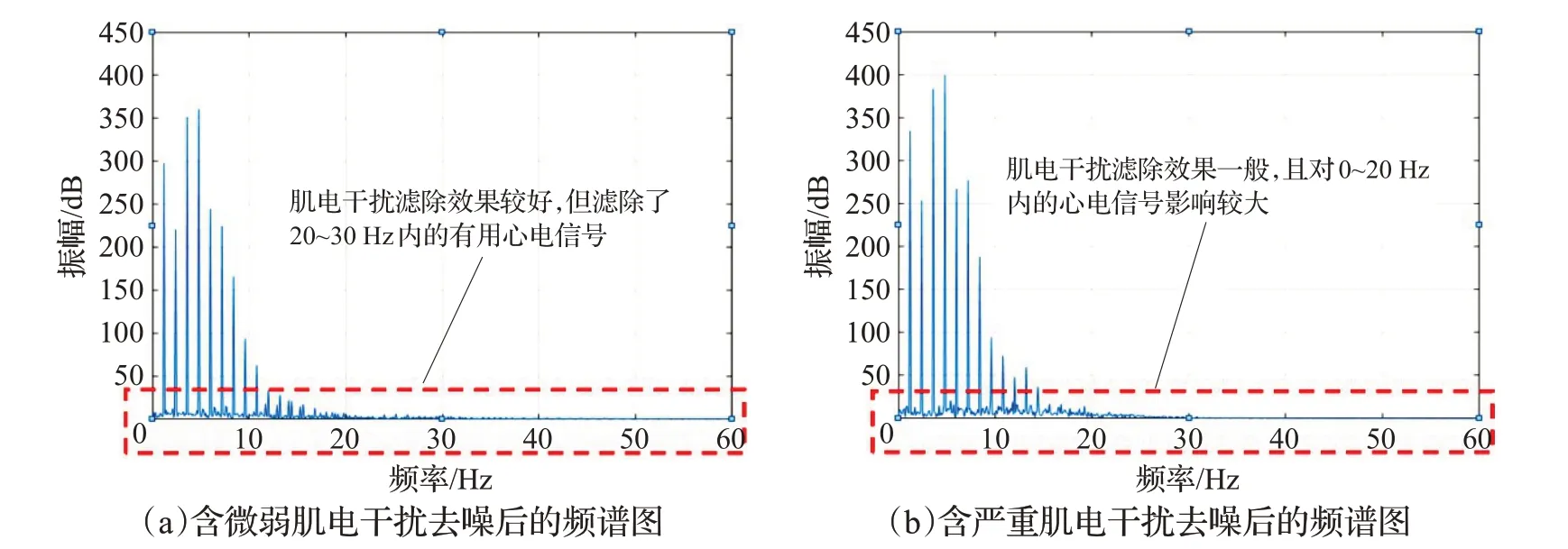
图17 经验模态分解法去噪结果Fig.17 EMD denoising results
低通滤波法是一种原理简单、操作方便的滤波方法。该方法通过对心电信号设置一个截止频率,使低于该频率的心电信号通过,而高于该频率的噪声成分被滤除,在实际去噪过程中,由于心电信号的频率主要集中在低频范围内,肌电干扰的频率往往高于心电信号的主要频率,因此也常用低通滤波法对心电信号的肌电干扰进行去噪。本文采用巴特沃斯数字低通滤波器对含肌电干扰的心电信号进行低通滤波,它的运算过程如公式(11)所示:

其中,H(s)表示含噪心电信号复频域的系统函数,ak和bm分别表示系统函数H(z)的分母系数和分子系数,x(n)和y(n)分别表示去噪前和去噪后的心电信号。经实验仿真后的心电信号去噪评估参数如表9所示,频谱图如图18(a)、(b)所示。
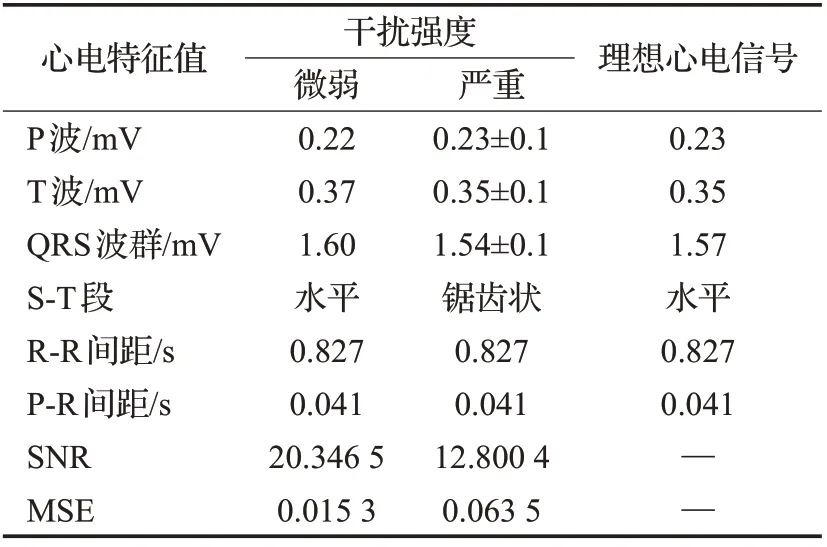
表9 低通滤波法去肌电干扰Table 9 LPF removes myoelectric interference
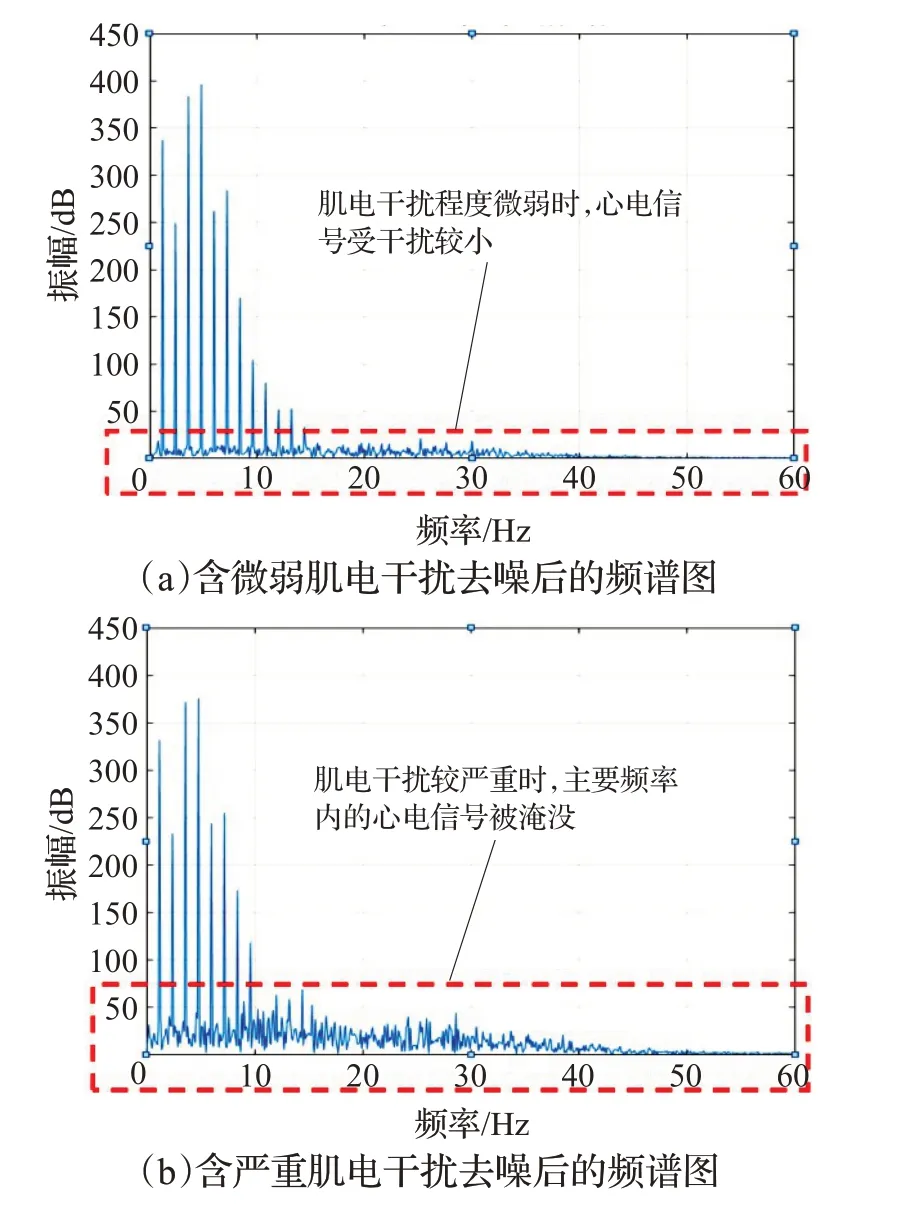
图18 低通滤波法去噪结果Fig.18 LPF denoising results
通过图18(a)、(b)可以发现,当肌电干扰程度较微弱时,心电信号的主要频率受干扰程度较小,当肌电干扰较严重时,心电信号的主要频率完全被肌电干扰的剩余残量所淹没。通过表8可以发现,对于微弱的肌电干扰,去噪后的心电信号特征值虽然有变化,但与理想心电信号差距不大,但当干扰强度加重时,心电信号完全被噪声淹没,无法读出准确特征值。
通过表7~9 可以获知,对肌电干扰去噪时,用小波阈值法去噪后的心电信号信噪比最高,均方差最低,去噪效果最好。经验模态分解法对轻微的肌电干扰滤除效果较好,但随着肌电干扰程度的加重,去噪后会对心电信号造成一定影响,信噪比略低于小波阈值法。低通滤波法可作为一个去除微弱肌电干扰的简单去噪方法,不适合滤除严重的肌电干扰,与上述两种方法相比,信噪比较低、均方差较高。
4.4 含多噪声的心电信号去噪方法
在实际情况中,所采集的心电信号往往含有多种噪声,研究得知,3 种噪声的频率分布不同,因此可以对3种噪声进行单独去噪,但肌电干扰的频率分布较广,与基线漂移和工频干扰容易发生重叠,因此3种噪声的去噪顺序不同也会对去噪结果造成影响,为了分析上述去噪算法对含有多种噪声干扰的心电信号去噪情况,本文选择对3种噪声去噪效果较好的小波变化法、陷波滤波法和小波阈值法,并模拟出同时含有两种噪声(基线漂移+工频干扰、基线漂移+肌电干扰、工频干扰+肌电干扰)和同时含有3 种噪声(基线漂移+工频干扰+肌电干扰)4种情况进行去噪顺序的分析。
通过前文的实验与分析可以发现,信噪比和均方差可以准确的反应出去噪效果的好坏,因此本节只采用信噪比和均方差作为去噪效果的评估标准,实验结果如表10所示。

表10 含有多噪声噪心电信号的去噪顺序比较Table 10 Comparison of denoising sequence of ECG with multi-noise
由表10获知,当含有两种噪声时,先滤除工频干扰的信噪比略高于先滤除基线漂移的信噪比,但对去噪结果影响不大,当含有肌电干扰时,先滤除肌电干扰会明显降低其他两种去噪结果的信噪比,因此含有肌电干扰和另一种噪声的心电信号在去噪时,先滤除基线漂移或工频干扰后再滤除肌电干扰的去噪效果较好。当含有3种噪声时,最后滤除肌电干扰的信噪比要明显高于其他情况,因此得出结论:包含两种噪声以上的心电信号,按照工频干扰、基线漂移、肌电干扰的去噪顺序去噪效果最好。
5 结论
本文采用模拟理想状态下的心电信号和模拟3 种噪声信号作为实验数据,对每种噪声分别选择3种去噪算法并通过计算信噪比、均方差和心电信号频域特征3种手段进行去噪效果评估,在此基础上,对同时包含两种以上噪声的心电信号的去噪方法进行了研究。研究结果表明:采用小波变换法、陷波滤波法和小波阈值法对心电信号中存在的基线漂移、工频干扰和肌电干扰去噪后的信噪比最高,均方差最低,去噪效果最好。当心电信号中包含两种及两种以上噪声时,基线漂移和工频干扰应该优先滤除,且优先滤除工频干扰的信噪比略高于优先滤除基线漂移的信噪比,而肌电干扰则需要最后进行滤除。
