温度交变下液态乙烷回气管线热应力数值计算与现场测试*

杨晓丽，张有兴，王晓磊，刘 涛，周兆明，张 佳

(1.新疆油田公司 采气一厂，新疆 克拉玛依 834000； 2.西南石油大学 机电工程学院，四川 成都 610500；3. 油气藏地质及开发工程国家重点实验室，四川 成都 610500)

0 引言

液态乙烷回气管线温度交变工况复杂，易产生管线低温疲劳。低温压力容器与常温压力容器的不同之处在于其破坏形式更趋向于脆性断裂，更容易失效[1-2]。此外，管线表面由裂纹引起的断裂是工程中最常见的失效模式。因此，正确评价含裂纹低温管线的危害性是整个管线系统最关心的问题之一。

目前大多数学者采用有限元方法求解管线不同参量下的热应力分布，以此来进行管线疲劳断裂分析。Du等[3]对稳态工况下的单管裂纹热应力进行了数值模拟和理论计算，结果得到引起塑性变形的最大应力发生在管线外壁；Sun等[4]利用有限元法计算了反应堆压力容器的温度场和应力场，通过对等效应力和周向应力的定量分析，利用扩展有限元(extended finite element method,XFEM)确定了裂纹在不同方向上的扩展路径及相应的应力分布；Si等[5]采用C(T)试样，对改进型X12Cr转子钢在600 ℃载荷条件下进行了蠕变疲劳裂纹试验，试验效果良好；Chen等[6]在有限元分析基础上，对核反应堆压力容器(reactor pressure vessel,RPV)承压热冲击的断裂力学进行了分析，结果表明裂纹前缘最深和裂纹表面上的位置最容易失效；Kandil[7]对稳态温压下压力容器应力分布进行了分析，结果得到不同工况下平均应力与应力幅值间的关系；Barsoum等[8]对不锈钢(SA 316L)高压釜进行了数值模拟，并进行了单轴拉伸试验和缺口环试件试验，得到了热压罐塑性和破坏模型的常数；陈俊文等[9]讨论了造成液态乙烷管线低温工况的诱因，并模拟了液态乙烷管线在特殊相变工况下的应力问题；刘卫国等[10]对温、压双重载荷作用下的高压埋地输气管线的动态响应进行了有限元分析，基于虚拟裂纹闭合技术(virtual crack closure technique,VCCT)获得了埋地输气管线的动态断裂参数；孙伟栋[11]使用ABAQUS软件对环向裂纹管线进行了数值分析，结论得到裂纹处存在明显的应力集中区，整体的应力值沿着管线轴向及裂纹走向逐渐减小。

目前国内外对稳态载荷作用下管线热应力分布的研究颇多，然而对低温交变载荷引起的管线失效问题鲜有报道，且尚未开展液态乙烷回气管线现场试验。此外，传统的输送管线应力校核模型不再适用于交变载荷工况。为此，本文建立液态乙烷回气管线三维有限元模型，采用间接耦合方式，计算低温管线温度交变耦合热力场，分析管线在交变温度载荷下的热应力分布规律。研究结果对降低管线运行失效风险、结构应力破坏风险和生产介质泄漏风险等具有重要指导作用。

1 基础理论

管线热应力分析遵循热弹性力学的平衡方程和变形连续方程[12-14]。考虑表面力与体积力作用的热弹性力学平衡微分方程如式(1)～(3)：

(1)

(2)

(3)

式中：Fx，Fy，Fz为单位体积力在x，y，z方向分量，N；∇2为拉普拉斯算子；e为应变；λ为拉梅系数；μ为泊松比；E为弹性模量，MPa；

热应力作用下管线的热应力和热应变可表示为应力及温度的函数，则将静应力控制方程的广义胡可定律进行修正，得到耦合控制方程如式(4)：

(4)

式中：σx，σy，σz为正应力，MPa；τxy，τyz，τzx为切应力，MPa；εx，εy，εz为正应变；γxy，γyz，γzx为切应变；u，v，w为任意点x，y，z方向的位移，m；G为切变模量，Pa；α为热膨胀系数，1/℃；t为温度变化量，℃。

2 管线基本参数与有限元模型

2.1 参数设置

某气田液化工厂液态乙烷回气管线如图1所示，材料为国产奥氏体不锈钢S30408(06Cr19Ni10)，室温平均线膨胀系数α=14.67×10-6/℃，弹性模量E=2.1×105MPa，泊松比μ=0.3。根据《压力容器》(GB 150—2011)表B.4，S30408高合金钢钢管在温度小于20 ℃和壁厚小于80 mm情况下，屈服强度为210 MPa，相应的许用应力为137 MPa，其具体性能参数如图2所示。管线通过法兰连接，介质流经法兰后在临近管线应力变化更大，此外，现场应力应变测试过程中发现管线表面存在大量的表面裂纹，管线最低操作温度-60 ℃，最高温度为环境温度。

图1 管线实物模型及示意Fig.1 Entity model and schematic diagram of pipeline

图2 S30408不锈钢参数Fig.2 Parameters of S30408 stainless steel

2.2 有限元模型建立

根据某气田液化工厂液态乙烷回气管线结构特点和载荷工况，采用有限元软件建立数值计算模型。管线外径为60 mm，壁厚3.5 mm(D60×3.5)，计算模型如图3所示。边界条件采用与现场真实工况一致，两端面均设置远端唯一约束，接管端部施加轴向平衡载荷。管线外部因保温材料的存在，设为绝热边界条件，热流密度接近于零。交变温度载荷分为2个过程进行，过程1：10～-46 ℃，过程2：-46～-2 ℃，操作压力0.6 MPa，计算时间为10 s。考虑到降温和升温过程的复杂性，分为2个计算步，第1个时间步为0.01 s，第2个时间步为0.1 s。网格划分采用四面体结构，裂纹处网格进行细化处理，整体质量在0.7以上。

图3 有限元模型示意Fig.3 Schematic diagram of finite element model

3 热应力分布规律数值计算

对不含裂纹和含裂纹2种工况进行管线疲劳寿命分析。由于温度均在设计范围内，因此，材料遵循弹塑性和线性本构关系，以等效应力屈服准则为评判标准。

3.1 无裂纹缺陷管线表面热应力分布

为了分析和比较沿管壁方向的应力，定义图3模型轮廓中心截面M。从图4可看出，随着时间的延长，管线整体热应力先增大再减小；0.2 s时最大等效应力为32.63 MPa；1 s时最大等效应力为52.26 MPa；5 s时最大等效应力为157.58 MPa，最大等效应力处于内壁；当10 s时，最大等效应力为74.51 MPa，最大等效应力处于外壁；特别的，5 s时管线应力达到最大，这是由于此时压力减小，温度逐渐回升，导致管内温差逐渐减小，根据弹塑性热应力理论公式，当温差减小时，对应的等效应力减小。图5为无裂纹时管线温度变化与应力的关系，可以看出温度先降低至-46 ℃，之后升高至-2 ℃；弹塑性范围内，温差与等效应力呈线性变化，应力呈先增大后减小的趋势。

图4 不同时刻管线横截面应力分布Fig.4 Stress distribution of pipeline cross section at different time

图5 无裂纹时管线温度变化与应力的关系Fig.5 Relationship between temperature variation and stress of pipeline without crack

3.2 表面裂纹缺陷对管线疲劳寿命的影响

根据最新的设计规范，结构表面主要缺陷为半椭圆形的形式，如图3所示。尺寸为3 mm×2 mm×0.5 mm(长×深×宽)。取截面M处外表面和内表面路径进行分析，内外路径如图3所示，其分析结果如图6所示。

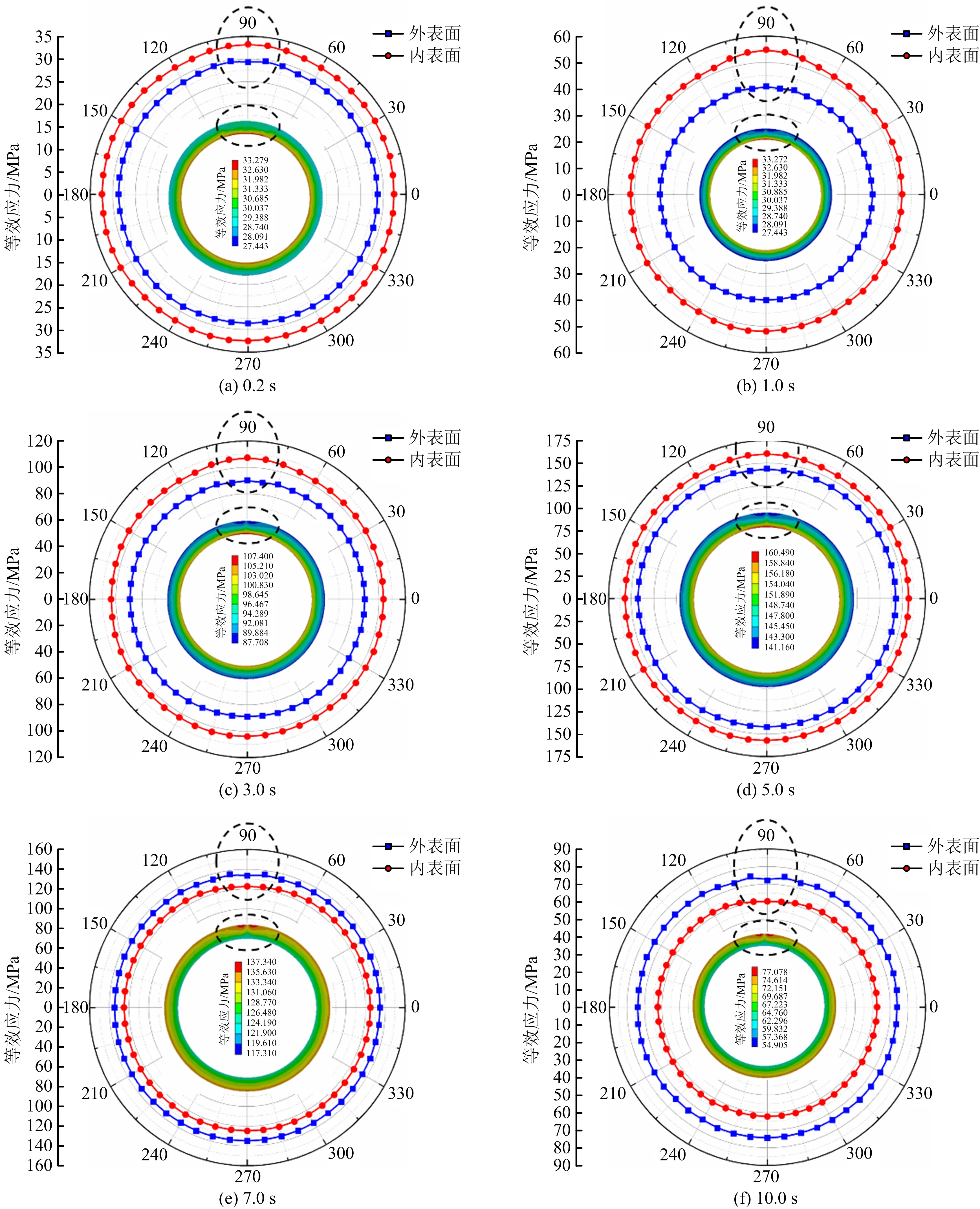
图6 不同时间含裂纹管线表面应力分布Fig.6 Surface stress distribution of pipeline with crack at different time

图6为不同时间下含表面裂纹管线表面等效应力分布，可以看出在低温交变载荷下，管线正上方(图6中90°位置)裂纹尖端处会发生疲劳损伤，裂纹周围局部区域存在应力集中；特别的，0.2 s时外表面最大等效应力为29.75 MPa，内表面最大等效应力为32.88 MPa，内表面等效应力大于外表面；1 s时外表面最大等效应力为40.98 MPa，内表面最大等效应力为54.80 MPa；3 s时外表面最大等效应力为92.80 MPa，内表面最大等效应力为105.01 MPa；5 s时外表面最大等效应力为143.76 MPa，内表面最大等效应力为160.40 MPa；前5 s计算可知，随着计算时间的增加，内外路径上等效应力逐渐增大，但内表面应力大于外表面应力。当7 s时，外表面最大等效应力为135.05 MPa，内表面最大等效应力为125.08 MPa；10 s时外表面最大等效应力为98.02 MPa，内表面最大等效应力为90.45 MPa；后5 s为回温阶段，随着计算时间的增加，内外路径上等效应力逐渐减小，但内表面应力小于外表面应力。

图7为不同时间管线平均等效应力，可以看出，5 s时管线裂纹处平均等效应力达到最大，之后等效应力减小，这是由于此时管内压力减小，温度逐渐回升，导致管内温差逐渐减小，根据弹塑性热应力理论公式，当温差减小时，对应的等效应力减小。

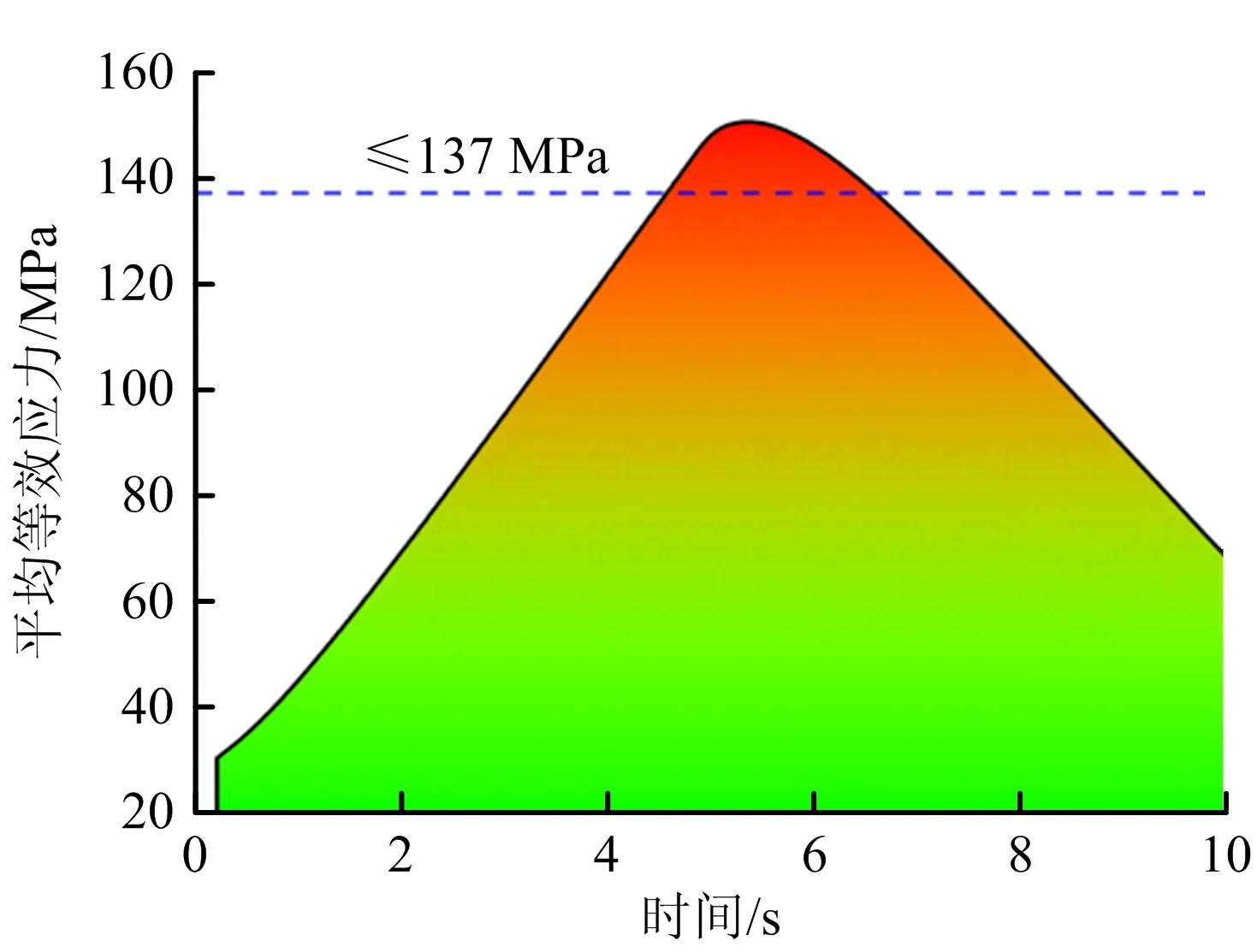
图7 不同时间平均等效应力Fig.7 Average equivalent stress at different time

4 试验模拟与分析

对某液态乙烷回气管线裂纹处进行现场应变试验，测试现场如图8所示。试验现场采用无线应变测试系统，无线设备节点1个(四通道ch1～ch4)；现场管线运行压力0.6 MPa，在管线表面布置4只应变片，分别呈90°布置，测量不同方位管线的应变变化。应变片粘贴前用砂纸取掉管线表面涂层，保证所粘贴的管线平面光滑、无划伤，应变片最大限度的与管线表面接触。操作前初始化系统所有通道，使其初始微应变为零，满足测试条件。液态乙烷回气分为2个过程：1)装车过程：液态乙烷加压温度降低；2)恢复过程：液态乙烷输管温度恢复到环境温度。

图8 现场测试Fig.8 Field test

从图9分析得出：随着管线温度的降低，应变成线性减小，随着温度变化稳定后趋于稳定；管线恢复室温过程与温度降低过程相反，逐渐增大，最后趋于稳定。为了表示微应变和等效应力的关系，将微应变统一化等效应力，如式(5)～(7)：

μτ=106ε

(5)

σ=E·ε

(6)

σ=0.2μτ

(7)

图9 现场测试结果Fig.9 Field test results

式中：μτ为微应变；ε为应变；E为材料的弹性模量，MPa；σ为等效应力，MPa。

装车过程微应变的变化范围为0～-491.95μτ，应力变化98.39 MPa；装车完毕后，微应变变化为0～724.640μτ，通过式(5)～(7)得到应力变化144.93 MPa。由表1可知，温降过程误差为0.4%，温升过程0.8%，仿真与实验数据吻合；通过现场试验数据对比理论计算，理论模型准确合理，可用于分析管线的热应力变化，同时为含缺陷管线的应力疲劳预测提供理论基础。

表1 仿真与试验数据对比分析Table 1 Comparative analysis of simulation and test data

5 结论

1)交变载荷下，沿管线壁厚方向的温度梯度明显减小。对于无裂纹管线，管内温度沿周向和轴向分布具有较大的不均匀性，温降阶段最大等效应力为157.58 MPa，处于管线内表面。温升阶段最大等效应力为74.51 MPa，处于管线外表面。

2)交变载荷下，管线裂纹尖端处产生了明显的应力集中，材料的韧性降低，增加了不稳定裂纹扩展的可能性。

3)温降过程误差为0.4%，温升过程0.8%，仿真与实验结果基本一致。理论计算模型准确合理，可用于管线热应力分析。