悬停状态双旋翼气动干扰与安全间隔研究*

2022-01-21谌哲宇储天羽高晟智董宇炜

中国安全生产科学技术 2021年12期

刘聪，谌哲宇，储天羽，高晟智，董宇炜

(中国民航大学空中交通管理学院，天津 300300)

0 引言

小型旋翼无人机具有低成本性、高适应性、可悬停及垂直起降的高机动性等优点，在物流、植保、安防等行业得到大量应用[1-2]，其运行安全性也逐渐引起重视[3-5]。但单机执行任务易受限，随着无人飞行技术的发展和任务的复杂化，多无人机编队飞行具有广阔发展前景[6-7]。与有人机类似，编队飞行提高任务执行效率的同时，多机之间的气动干扰效应不容忽视。当后机处于前机的涡流场中，后机气动力变化，严重影响后机的飞行稳定性，若无法操控则有坠机的风险[8-9]。旋翼为无人机主要动力部件，是产生气动力和涡流场的主要来源。因此，有必要针对不同间隔的布局形式，分析无人机旋翼间的流场干扰特征，并定量给出间隔与气动力参数的对应关系，这有助于近距密集编队飞行时旋翼无人机间的安全间隔设置并制定安全的飞行控制策略。

在无人机旋翼间的气动干扰研究方面，郭瑞雪等[10]总结了国内外研究现状，多旋翼飞行器气动干扰特性受到自身翼间干扰和非定常来流影响，并且指出使用计算流体力学CFD方法模拟分析相邻旋翼流场的叠加和干扰的细节特性是可行且必要的。沈奥等[11]使用CFD方法模拟了旋翼无人机单机悬停状态和飞行状态的流场，根据单机流场定性划分了不同区域，指出了区域不同会对密集编队时的气动产生影响，但未针对双机或双旋翼进行模拟并给出定量的结果。纵向间隔的研究以共轴双旋翼为代表，因其优良的升力特性被直升机和无人机等广泛采用，共轴双旋翼的气动干扰机理[12-14]进行较深入研究。但共轴双旋翼的共轴结构决定了两旋翼仅有纵向间隔。另外，雷瑶等[15]和李沛等[16]等从无人机的设计布局角度研究了旋翼间距对旋翼飞行器气动性能的影响，试图找到最优的旋翼间距。此间距为横向间隔，即旋翼的旋转面在同一平面内。以上关于双旋翼间气动的干扰研究，增强了对其流场作用机理的了解和认知；但是，双旋翼的位置关系大多局限在仅有纵向或横向的单一间隔，同时存在横向和纵向间隔和气动干扰研究则很少涉及，而这在无人机编队飞行时为常见形态。

因此本文拟以双旋翼单元为研究对象，主要采用计算流体力学CFD仿真的方法，分析悬停状态时双旋翼处在不同横向和纵向间隔位置时的流场特征和气动参数变化情况，为无人机编队时的安全间隔布局提供理论参考。

1 计算模型和方法

1.1 几何模型

无人机旋翼为其主要动力部件，旋翼之间的气动干扰直接影响整机的稳定性，为简化研究，暂不研究机身与旋翼之间的干扰。本文研究采用的无人机旋翼模型如图1所示，桨半径11.94 cm，桨距12.70 cm，此类桨广泛应用于大疆精灵系列无人机。沿半径方向其弦长和扭转角度变化较大，分布如图2所示。在29%相对半径位置附近扭转角和弦长取得最大值，最大扭转角和平均扭转角分别为19.04°和12.75°，最大弦长和平均弦长分别为6.06 cm和2.00 cm。

图1 旋翼模型Fig.1 Rotor model

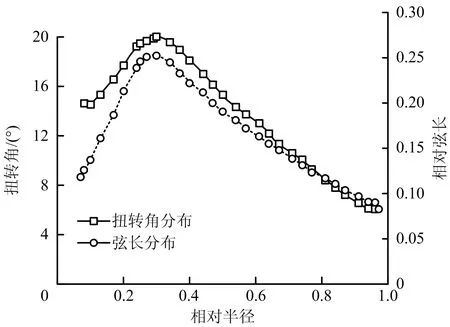
图2 沿半径方向弦长和扭转角分布Fig.2 Distribution of chord length and twist angle along radial direction

1.2 计算域和网格

对旋翼流场的仿真采用多重参考系方法(Multiple reference frame，MRF)，经与实验对比该方法使用于旋翼的流场仿真[17]。此方法需要将计算域划分为包含旋翼在内的旋转域和外部静止域，如图3所示：静止域尺寸为5D×2D×10D，旋转域直径1.1D，厚度约0.13D。旋转域网格保持静止，设置其旋转坐标系并以作用的科氏力和向心力来定常计算；静止域按惯性系坐标进行计算；旋转域与静止域间通过交界面传递流动参数。当分析2个旋翼间隔影响时，固定1#旋翼，移动2#旋翼相对水平位置X/D和相对竖直位置Z/D。

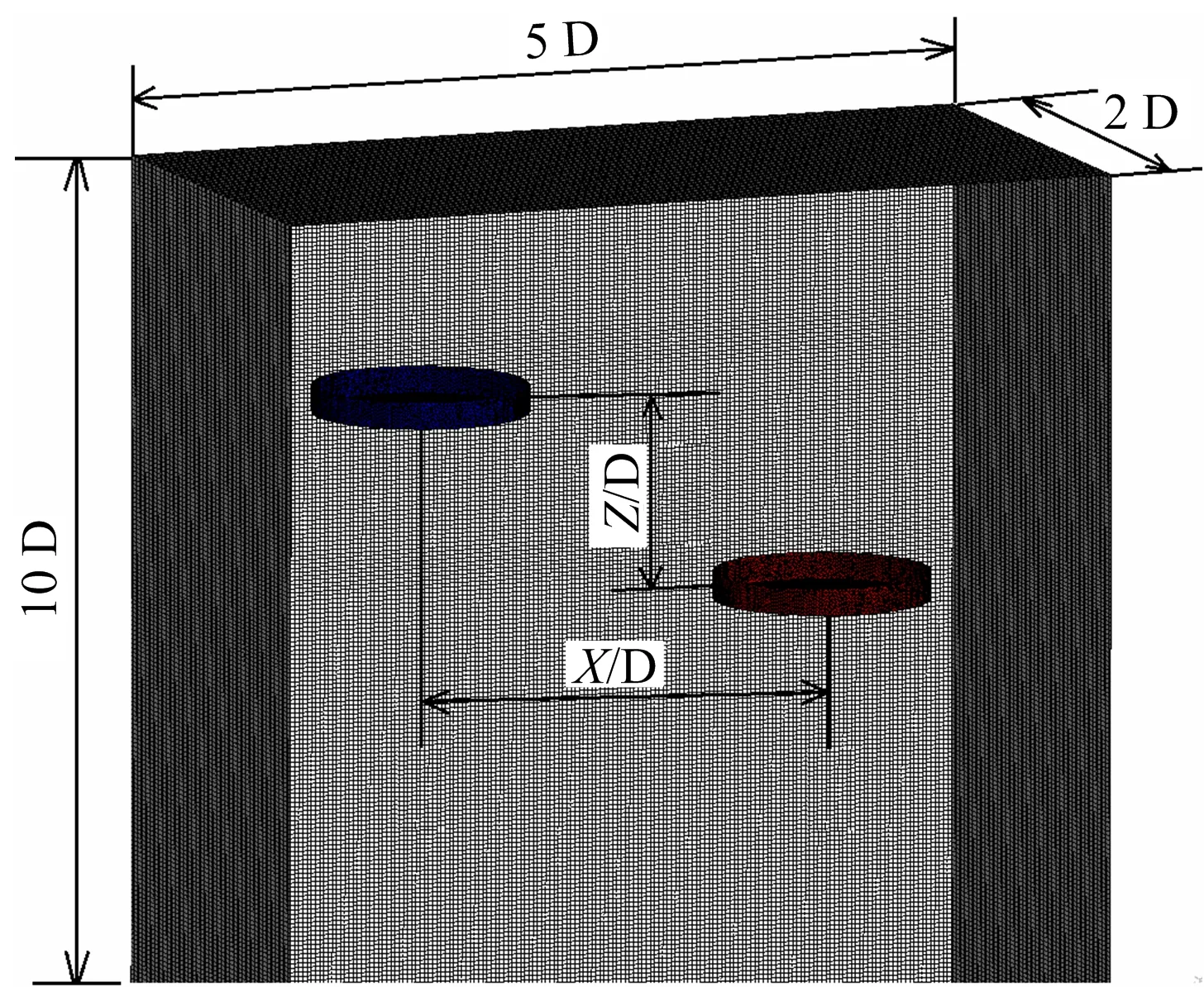
图3 计算域Fig.3 Computational domain

计算域流场采用结构-非结构混合网格进行划分，网格单元总共约980万。其中静止域采用结构网格，约400万网格单元；2个旋转域采用非结构网格，各290万。过旋翼竖直截面的网格如图4所示。为更好捕捉旋翼流场特征，对旋翼壁面及其前后缘位置进行网格加密，如图5。另外，旋翼表面采用棱柱网格划分10层边界层网格，并保证第1层网格对应y+在1附近。

图4 中截面网格Fig.4 Mesh of middle section

图5 旋翼壁面网格Fig.5 Mesh of rotor wall

静止域外流场6个边界设置为压力出口边界条件，模拟静止无穷远的环境；静动域的交界面设置为interface边界；旋翼表面设为无滑移壁面边界，并指定旋转域的旋转中心和转速。

1.3 控制方程和计算方法

小尺寸旋翼根据其直径D(0.239 m)和设计转速(5 000 r/min)，桨尖线速度约60 m/s，马赫数Ma<0.3，雷诺数量级105，可认为不可压缩流。故本文采用不可压且有黏的三维N-S方程模拟流场，采用有限体积法对方程进行空间离散，控制方程如式(1)所示：

(1)

矩阵向量U、F、G、H和J如式(2)～(6)所示：

(2)

(3)

(4)

(5)

J=[0ρfxρfyρfzρw(ufx+vfy+wfz)]Τ

(6)

式中：x,y,z分别为三维坐标方向；t为时间;ρ为密度，kg/m3;V为合速度;u,v,w分别为x,y,z方向的分速度，m/s;p为静压，Pa;e为比内能，J/kg;fx，fy，fz分别为x，y，z方向的粘性切应力，N/m2。

采取SIMPLE算法进行速度场和压力场的耦合。湍流模型选用SSTk-ω模型，该模型结合了自由流中的k-ε和近壁的k-ω模型优点，适用于旋翼气动的仿真模拟，并采用二阶格式对压力、动量、能量和湍流项进行差分求解。以计算残差小于1×10-4作为收敛判断标准。在2.1节中将对此计算方法进行实验验证。

1.4 计算工况和参数定义

本文研究主要分析旋翼不同位置间隔下的干扰情况，计算工况主要改变旋翼间的横向间隔X/D和纵向间隔Z/D，具体间隔设置如表1所示。

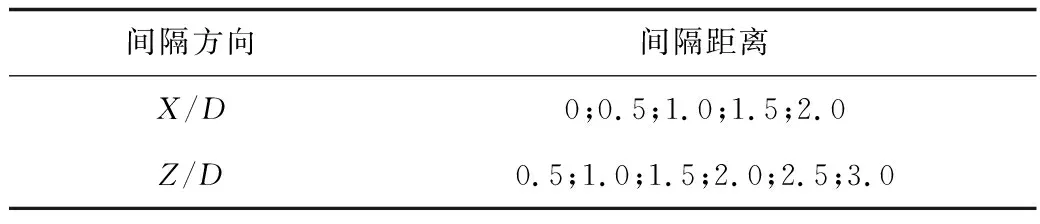
表1 计算工况Table 1 Calculation conditions

结果分析时使用无量纲系数评估流场干涉下旋翼的气动性能，即拉力系数CT、扭矩系数CQ、俯仰力矩系数CM。其定义式如式(7)～(9)所示：

(7)

(8)

(9)

式中：T为旋翼拉力，N；Q为旋翼扭矩，N·M；M为水平内的合力矩，N·M；R为旋翼半径，m；Ω为旋翼角速度，rad/s；ρ为空气密度，取1.225 kg/m3。

2 结果与分析

2.1 单旋翼流场仿真结果与实验验证

下文展示单个旋翼在不同转速下的气动特征，作为双旋翼干扰结果的对比基准；并与实验结果对比，验证数值模拟方法的准确性。图6～7为2 000,5 000,8 000 RPM的中截面速度和涡量仿真结果。从速度云图上看，每侧桨叶下方形成1股高速区，且向外半径方向向外扩散；同时在中心区域，由于高速气流诱导，形成1股较低速度区。随着转速升高，旋翼下方气流速度增大同时，扩散范围逐渐增大。从图7涡量云图上看两侧桨尖形成的桨尖涡最为明显，内部则诱导出较为复杂的二次涡系。结合速度和涡量的仿真结果，当转速为5 000 RPM时旋翼下洗流场主要影响区域在X=1.5D、Z=2.0D范围内；当转速为8 000 RPM时，此区域扩展为约X=2.0D、Z=3.0D。因此进行2个旋翼干扰分析时，设置双旋翼的相对位置间隔覆盖单个旋翼流场影响范围。

图6 旋翼截面速度分布Fig.6 Velocity distribution of rotor section

图7 旋翼截面涡量分布Fig.7 Vorticity distribution of rotor section

图8为单旋翼气动性能测试台。该实验台用于测试定距螺旋桨或旋翼的拉扭曲线和力效实验等，也可置于风洞中测试飞行状态的性能数据。实验台主要由动力系统、传感器系统和数据采集系统组成。动力系统由电池、电调和电机组成，用于驱动旋翼旋转，控制信号由上位机发出，通过PWM信号控制电机转速，实验转速范围为2 000～8 000 RPM；传感器系统主要测量参数为输入电压、电流、转速、电机温度和旋翼拉力、扭矩。传感器测量信号通过16位高速数据采集系统采集和处理数据。实验台的测量误差主要取决于各传感器的测量精度，主要参数相对误差如表2所示。

图8 单旋翼气动性能测试台Fig.8 Test system for aerodynamic performance of single rotor

表2 实验参数相对误差Table 2 Relative errors of experimental parameters

数值仿真和实验结果对比如表3所示。可以看出，当转速较低时，拉力系数和扭矩系数的计算误差较大，这主要是由于低转速下拉力和扭矩的绝对值均较小，放大了实验和模拟的相对误差；在中高转速时，拉力系数和扭矩系数的相对误差较小，且比较稳定，分别约5%和9%。上文的研究中旋翼转速设定在悬停设计转速5 000 RPM。

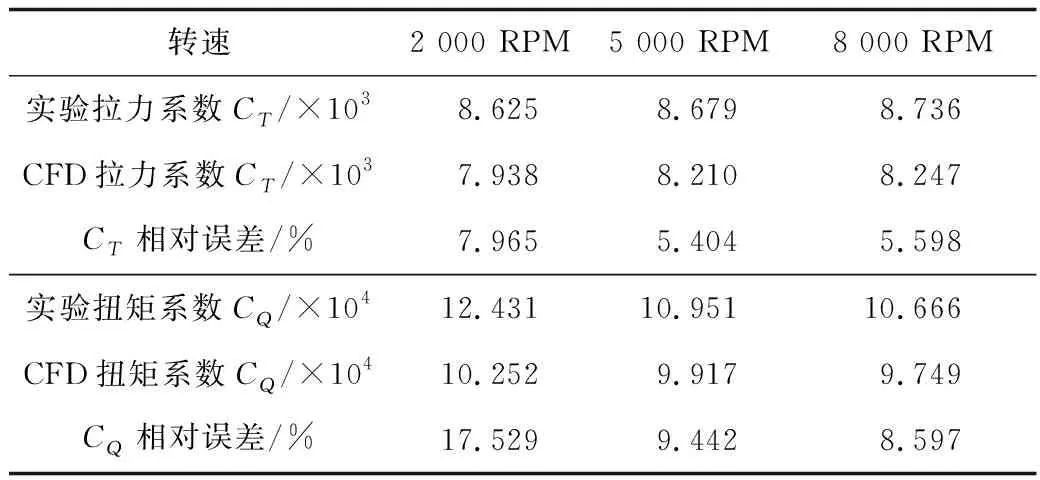
表3 单旋翼仿真与实验结果对比Table 3 Comparison on simulation and experimental results of single rotor

2.2 不同间隔下双旋翼的流场分析

为分析在不同间隔距离下的双旋翼流场干扰情况，进行速度场和涡量场的对比，分别如图9和图10所示。从图9～10中可以看出，无论是速度场还是涡量场，1#旋翼基本不受影响，而2#旋翼所受影响非常明显。因此，着重分析2#旋翼的流场变化。

图9 不同间隔双旋翼截面速度分布Fig.9 Velocity distribution of twin rotors sections with different separations

图10 不同间隔双旋翼截面涡量分布Fig.10 Vorticity distribution of twin rotors sections with different separations

当两旋翼之间无横向间隔，即2#旋翼位于1#旋翼的正下方时，2#旋翼的下洗气流受1#旋翼气流限制，未呈现出扩散趋势，速度和涡量场反应出其下洗气流局限在旋翼下方1.0D范围内，且高速区和高涡量区纵向范围缩小。此时，流场分布仍保持对称形态。

当2#旋翼在横向具有0.5D和1.0D间隔时，2#旋翼下洗流场出现非对称特征，这主要由2#旋翼两侧桨叶上游来流的非均匀性决定。如图9(b)～(c)和图10(b)～(c)所示，2#旋翼主要处于1#旋翼右半侧桨的下洗流中，此部分气流除具有垂直速度外，还具有与右半桨旋转线速度同向的水平分速度；2#旋翼左半侧桨旋转速度方向恰与1#旋翼右半侧桨相反，即对于2#旋翼左半侧桨来说，相当于增大了其来流的相对速度。同理，2#旋翼右半侧桨的相对来流速度相应减小。另外竖直间隔不同，两侧来流的竖直速度分量也不同，同样也会加剧此非对称性。总体来说，2#旋翼相对1#旋翼向右侧偏置，增强了2#旋翼下洗左半侧气流的速度和涡量，而右半侧气流的速度和涡量则相对减弱；右半侧的下洗流在横向的扩散受到限制，这与无横向间隔时相同。此非对称性的流场分布，还会体现在对无量纲气动参数，尤其是对俯仰力矩系数的影响上，将在下文中讨论。

当双旋翼的横向间隔在1.5D及以上时，旋翼流场干涉现象基本消失。纵向间隔1.0D时，1#旋翼下洗流不经过2#旋翼旋转盘面，即使两者的下洗流场有所干涉，但影响不大；当纵向间隔在2.0D及以上时，2#旋翼来流即使受到1#旋翼下洗流影响，但由于距离较远，来流速度较低，涡强度也较弱，未对2#旋翼产生明显影响。

2.3 不同间隔下双旋翼的气动参数结果

当旋翼间存在气动干扰时，改变流场分布同时会引起旋翼气动力和气动力矩的显著变化。图11～13分别给出了双旋翼在不同间隔下的拉力系数、扭矩系数、俯仰力矩系数变化曲线。1#旋翼的气动力和力矩系数并不受间隔的影响，2#旋翼的气动参数则变化剧烈。

图11 不同间隔的拉力系数曲线Fig.11 Tension coefficient curves under different separations

图12 不同间隔的扭矩系数曲线Fig.12 Torque coefficient curves under different separations

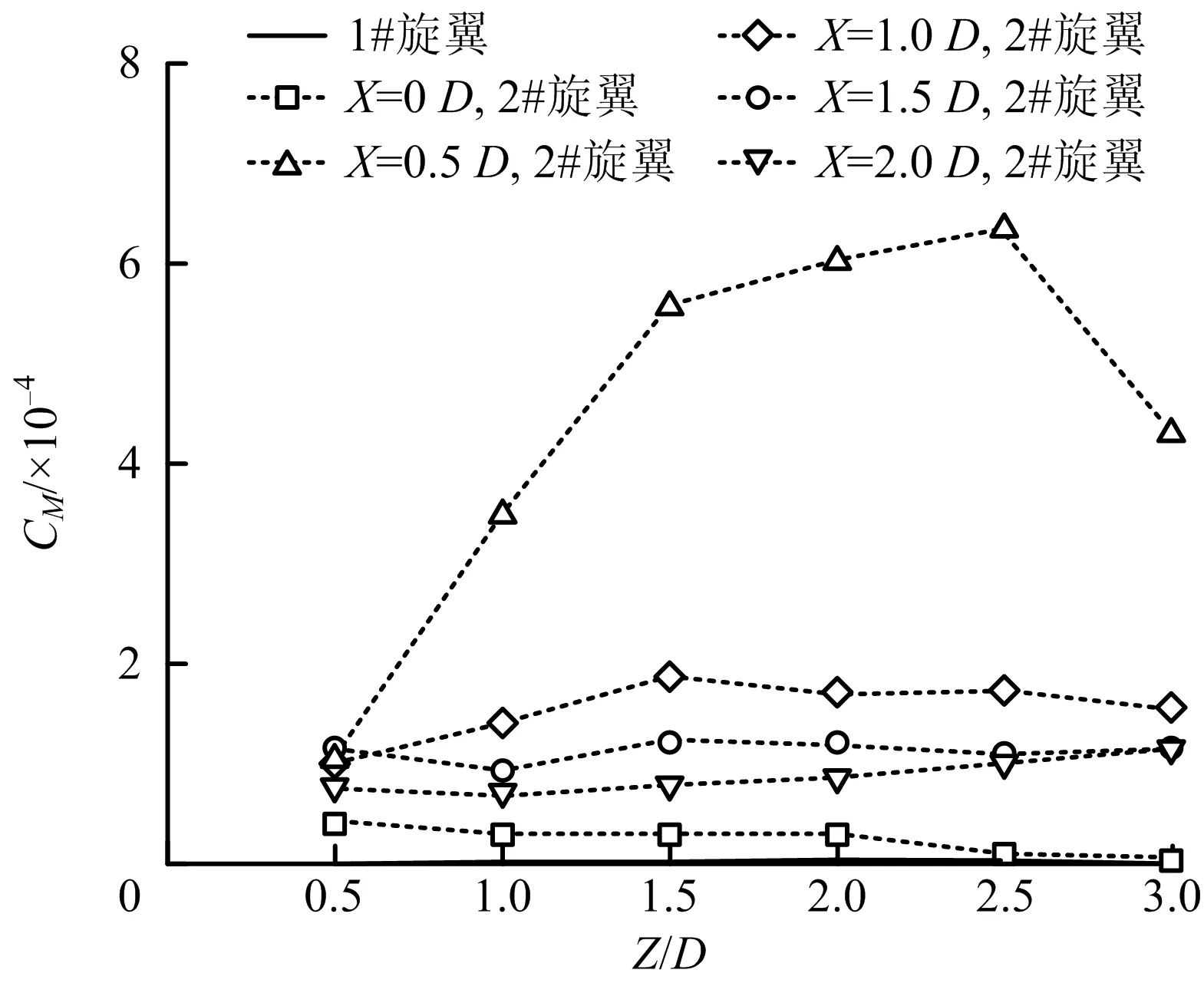
图13 不同间隔的俯仰力矩系数曲线Fig.13 Pitching moment coefficient curves under different separations

从拉力系数变化曲线可看出，2#旋翼处于1#旋翼的下洗流中时，造成其旋翼拉力下降；当2#旋翼位于1#旋翼的正下方时，其拉力损失最大，且纵向间隔越小，拉力减小越明显。间隔X=0.0D，Z=(0.5-1.5)D范围内，拉力系数减小约50%；当横向间隔X=0.5D和1.0D时分别减小约20%和10%；此种现象主要原因是上游旋翼下洗气流产生向下的诱导速度，减小了旋翼剖面迎角，进而减小了拉力。当横向间隔X≥1.5D以上时，2#旋翼受来流的向下诱导速度影响较小，其拉力则基本不受影响。

扭矩系数反映了旋翼气动阻力的大小。从图12可以看出，2#旋翼扭矩系数受影响最严重区域为横向间隔X=0.0D，即正下方区域，其扭矩减小；且随着纵向间隔越小，扭矩减小越明显，当Z=0.5D时减小约20%。而当存在横向间隔时，除了X=0.5D,Z≤1.0D区域，2#旋翼扭矩则相对增大，不过增大幅度在10%以内。此主要原因如上文所述，当2个旋翼横向错置时，2#旋翼的半侧旋翼主要位于1#旋翼下洗流中，其旋转线速度方向与下洗流的水平分速度方向相反，因此增加了旋转的气动阻力；当无横向间隔时，2#翼的旋转方向与来流水平分速度方向相同，则减小了气动阻力。

俯仰力矩系数反映了旋翼当前的水平稳定状态，当俯仰力矩系数为零时，旋翼可保持水平状态；当此系数大于0时，则说明此旋翼在俯仰力矩作用下，有倾覆的危险。从图13中可以看出，当无横向间隔X/D=0时，虽然2#旋翼完全处于下洗流区，但由于流场仍可保持对称性，两侧的半旋翼气动力的变化相差不大，其俯仰力矩系数很小。X=0.5D且1.0D≤Z≤3.0D区间为最危险区域。从上文的流场分析可知，此时2#旋翼的流场出现显著的非对称特征，两侧旋翼的气动力不平衡。当横向间隔X/D继续增大，2#旋翼逐渐离开下洗流区，非对称流场现象减弱，俯仰力矩系数也逐渐减小。