基于大数据的配电网故障诊断预测模型设计

程晓磊，王鹏，王渊，赵嘉冬

（内蒙古电力经济技术研究院，内蒙古 呼和浩特 010090）

随着社会经济的发展和人民生活水平的不断提高，电力系统能够直接影响人们的日常生活，配电网使用者对电网的安全性和可靠性的要求越来越高。随着人口数量的剧增，电荷负载不断加重，导致配电网中的数据量呈现海量增长趋势。大数据环境对电网结构造成对配电网故障诊断和预测的难度逐渐增大，配电网的安全问题日益突出[1]，配电网安全事故频频发生。构建可以预测大数据环境下配电网故障发生位置的故障诊断模型是提高配电网可靠性和安全性的重要手段[2]。传统基于无线传感器的配电网故障诊断预测模型，对大数据环境下的配电网数据实施诊断过程中，存在故障位置判断不准确且耗费大量时间、配电网的经济效益较低的严重问题[3]。因此，文章设计基于大数据的配电网故障诊断预测模型，增强对配电网故障检测的正确率，促进配电网的循环利用，提高配电网的生命周期，节约经济成本。

1 基于大数据的配电网故障诊断预测模型

1.1 基于RS-IA模型的故障定位

本文基于大数据的配电网故障诊断预测模型，故障定位利用的是一种基于粗糙集理论的免疫算法（rough-set-immune-algorithm，RS-IA）模型，RS理论能高效地对不准确、模糊的数据进行有规律的总结，总结其中的深层含义；IA可对故障信息进行大规模智能搜索[4]，削弱冗余数据的干扰并寻找最优解。本文利用RS-IA模型进行配电网故障诊断位置的定位步骤如下：

1）根据配电网的相关理论，构建配电网故障诊断预测挖掘数据库；

2）对故障发生位置特征进行提取，确定与之对应的条件属性和决策属性；

3）根据步骤2）确定的属性特征，将配电网的故障转化为RS决策表；

4）将RS决策表的求约简问题转变为求区分矩阵最小约简数的问题，并利用IA进行求值；

5）从得到的最简约简集合中获得所需规则；

6）根据得到的规则对配电网发生故障位置进行诊断预测，利用IA求解最小约简数算法，步骤如下：对决策属性D对条件属性C的依靠值KC进行计算[4]，并假设Cone(C)=∅，依照顺序将条件属性中单个存在的属性进行剔除且a∈C，若存在KC-a≠KC，即 得 到 Cone(C)=Cone(C)⋃ a，核 用Cone(C)表示；若 KC-a=KC，此时的 Cone即为最佳的属性约简。

本文对初始抗体群的编码方式采用二进制的编码，条件属性C与抗体长度相对应，抗体中基因表示条件属性是否保留，0表示抛弃该条件属性，1表示进行约简计算时保留该条件属性。初始化核的条件属性对应位取1并进行保留，其它位保留还是抛弃随机选取[5]，因此得到抗体表达式为[0，1，1，…，0，1]，该式即为初始抗体群N。通常对计算结果的满意度用亲和力表示，文章计算抗原和抗体的亲和力，其中亲和力值越大，表示得到的数据可信度越高，本文采用适应度函数的倒数为亲和力函数，适应度函数表达式如下：

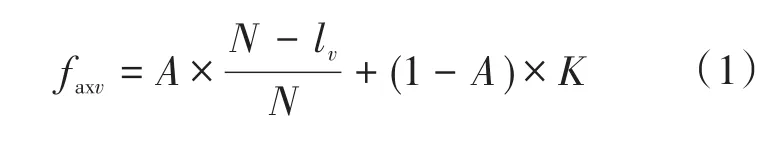
式中：N为条件属性的数值；lv为抗体v中包含“1”的数量，与进行约简完毕后的条件属性的数量相同；K，A分别为抗原和抗体的依赖程度以及调节因子。

对两个抗体的亲和力进行计算：

式中：differvw为抗体间结合强度的大小，大小不同表明相同抗体位置携带不同编码基因数量不同。

计算抗体v的种群计算公式如下式所示：

式中：Tac1为确定的固定免疫选择值。

应对抗体进行促进或抑制操作[5]。促进操作可增大抗体的多样性，提高亲和力，但抗体浓度过高时亲和作用可能被抑制，需要降低抗体浓度，记忆库中的数据应随时更新；抗体之间不断进行交叉变异构成下一代的新抗体群，若满足最终条件则结束，否则回到步骤3）。

由计算得出的最优属性的约简，进而得到决策规则，可将配电网故障诊断与决策规则相结合，对配电网故障发生位置进行迅速定位，实现配电网故障的初步诊断。

1.2 基于模糊积分的故障诊断预测模型

基于上文获取的配电网故障初步诊断结果，将电网的拓扑关系与之结合，计算各故障信息对故障元件的支持度，采取模糊积分的信息融合实施故障判断，可以对样本训练和拓扑变化问题进行改进[6]，使故障诊断的效果得到加强。提高配电网大数据的运算速率可诊断出多种故障，是实现高效、快速诊断和预测大数据环境下配电网故障位置发生的重要手段。本文基于大数据的配电网故障诊断预测模型的综合诊断框图如图1所示。图中，基于RS-IA模型获取的配电网初步故障信息，对该故障信息进行数据预处理，再对故障元件实施初级判断，在此判断基础上融合配电网的拓扑关系实施模糊积分故障诊断，得到配电网故障诊断结果。

图1 故障诊断框结构图Fig.1 Structure diagram of the fault diagnosis box

故障信息预处理功能为确定发生故障元件同时进行信息分类，当配电网系统发生故障时，系统会自动进行故障位置断开[7]，造成部分区域发生断电，初步判断故障位置在断电区域，接下来即进行断电区域故障诊断。通过实时接结线分析法判断故障位置前后的拓扑结构差异，实现对故障位置的准确定位，故障发生位置处的电力元件即为故障元件。本文基于大数据的配电网故障诊断预测模型对继电器进行简化，在输入故障信息前还需对故障信息进行解析和分类[8]，如添加第一和第二后备保护，将高频、差动以及过流等保护措施划分归类。

1.2.1 数学描述模糊积分

数学角度分析模糊积分是基于模糊测度的非线性运算，模糊积分概念的提出主要目的是利用其进行解决各相互独立因子之间存在的交互影响。

假设一个非空集合X，Y是集合X下的一个非空子集，现规定集合Y的非负数的广义实数集函数u:Y→[0,∞]是模糊测度，并且满足如下特点：

1）u(φ)=0 u(X)=1(正则性 )；

2）∀A,B⊂ Y,A⊂ B ⇒ u(A)≤ u(B)(单调性 )；

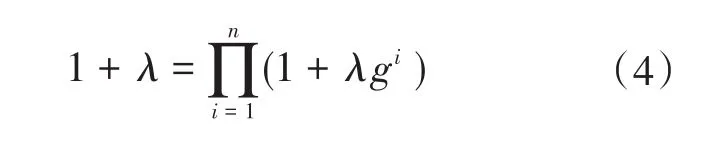
能够得到唯一确定λ＞-1且λ≠0。

依照函数f(x)各个故障信息的客观数值对集合X排序，降序排列形式如f(x1)≥f(x2)≥…≥f(xn)，则模糊测度g(xi)的求解过程如下：

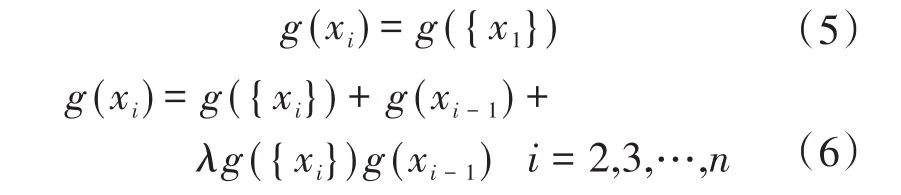
常用的模糊积分方式为Sugeno模糊积分和Choquet模糊积分，但Sugeno模糊积分自身舍弃可加性[10]，在应用过程中限制作用较明显，本文为规避该问题，模糊积分方式应用Choquet模糊积分。

当确定集合X的模糊测度g后，能够得到函数关于模糊测度g的Choquet模糊积分表达式：

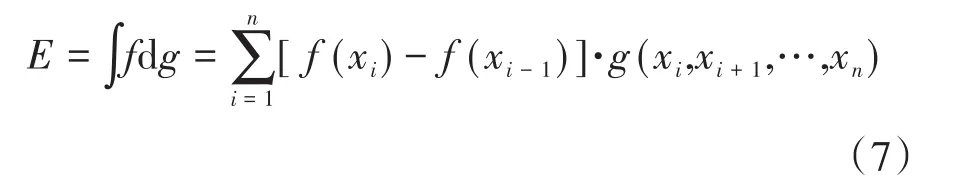
式（7）中，函数f(x)存在f(x1)≥(x2)≥…≥f(xn),f(x0)=0，则经Choquet模糊积分后的E值为经诊断得到的配电网故障可能指标。

1.2.2 初级诊断结果预处理

当诊断结果显示该处无故障或与之相连的元件也无故障时，该结果表明自身故障对相连元件的支持度为0。但实际诊断出的结果是不为0的，对结构较复杂的元件来讲，会造成故障指标偏大[11]，容易造成故障元件错判。Choquet模糊积分的单调属性会对诊断结果造成影响，因此对1.2.1小节获取的配电网故障初级诊断进行预处理十分重要，本文采用模糊技术进行预处理，选择的隶属度为

式中：x，y分别为输入数据和输出结果。

本文配电网故障诊断预测模型中，设置x1和x2的数值分别为0.1和0.4，规定f(x1)的值为0.01，因为x=x2处连续，得到c和a的值分别是0.429 1和0.072 7。

1.2.3 确定模糊测度

配电网自动化装置会受到各种因素的干扰，故障信息对不同关联强度的元件支持度也不尽相同，等同于模糊测度的不同。测量模糊测度通常采用样本测试、准确性比较以及专家经验三种方式，要想准确地进行元件的故障诊断，需将初级诊断结果与配电网的拓扑结构相结合[12]，本文方法模糊测度的确定依靠专家的经验。将专家经验与实际情况结合，表1为确定故障元件诊断结果的模糊测度表。

表1 故障元件的模糊测度Tab.1 Fuzzy measure of faulty components

1.2.4 故障诊断流程

本文基于大数据的配电网故障诊断预测模型中应用模糊积分融合技术对配电网故障诊断总流程如下：

1）对故障发生前后配电网的拓扑信息进行提取，构成故障元件的候选集合X={x1,x2,…,xn}；

2）配电故障信息预处理并对继电器的保护数据进行分析整理；

3）对不同的候选元件实施故障诊断[13]；

4）对经过RS-IA模型进行初级诊断后的结果进行预处理；

5）由配电网的拓扑信息，能够得出不同候选元件直接相连的元件的集合Xi-indirect={xm,…,xn}以及隔一级相关联的集合Xi-indirect={xk,…,xl}；

6）确定故障候选元件xi以及关联元件的情况，根据上文中的式（4）～式（6），其中，式（4）确定λ，模糊度测度gλ根据式（5）和式（6）求出；

7）根据拓扑信息以及元件的诊断结果[14]，形成与故障候选元件xi直接相连元件支持度集合Fi-direct={fm,…,fn}以及隔一级相关联元件支持度集合Fi-indirect={fk,…,fl}；

8）由式（7）计算得到的模糊积分值，即为本文模型的综合诊断可能指标[15]，构成故障可能性指标集合E={e1,e2,…,eN}；

9）由得出的故障可能性指标集合确定配电网故障发生的元件。

2 实验分析

为验证本文模型的优越性，将本文模型与基于RS-GA数据挖掘模型应用于配电网故障诊断中，求得的最优属性约简个数以及用时情况进行比较。实验在Matlab环境下构建两种配电网故障定位程序，对某市的大规模配电网进行故障定位。为保证实验对比结果突出，两个模型的其余参数应保持一致，表2为两个模型的最佳属性约简个数及用时结果。

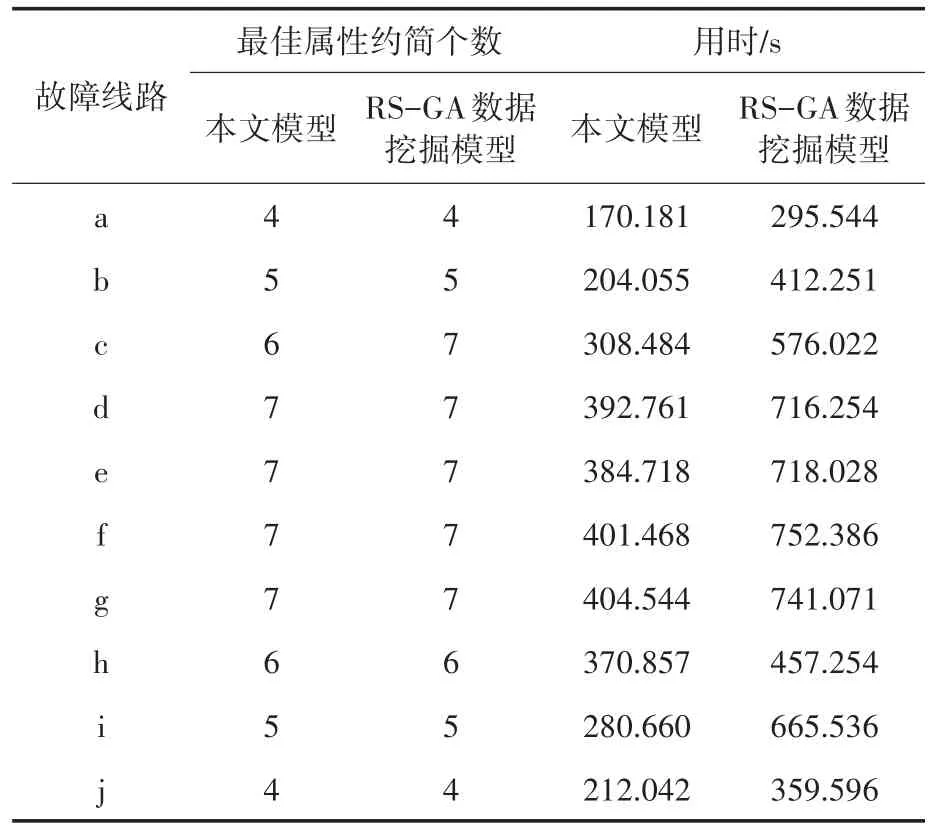
表2 两个模型测试结果Tab.2 Two model test results

从表2可以看出，实验环境与设备等配置都相同的情况下，本文模型在用于检测规模较大的配电网故障诊断中能较好地计算出最佳属性约简并且故障检测的用时也较短，且本文模型在进行故障定位过程中导入抗体浓度，能有效防止出现局部过度收敛现象，使故障定位的准确率得到提高，提高本文模型的可信度。

基于大数据的配电网故障诊断预测模型中运用本文Choquet模糊积分在故障定位精度和运算速率上具有较大的优势。Sugeno模糊积分与Choquet模糊积分在数据预处理过程相似。为进一步测试本文模糊积分应用于本文模型进行故障定位的效果，现利用Sugeno模糊积分、上积分和下积分作为对比实验，比较4种模糊积分方法在得到适应度值为0时的迭代次数，且设置最大迭代次数N不超过100，仿真计算结果如图2所示。

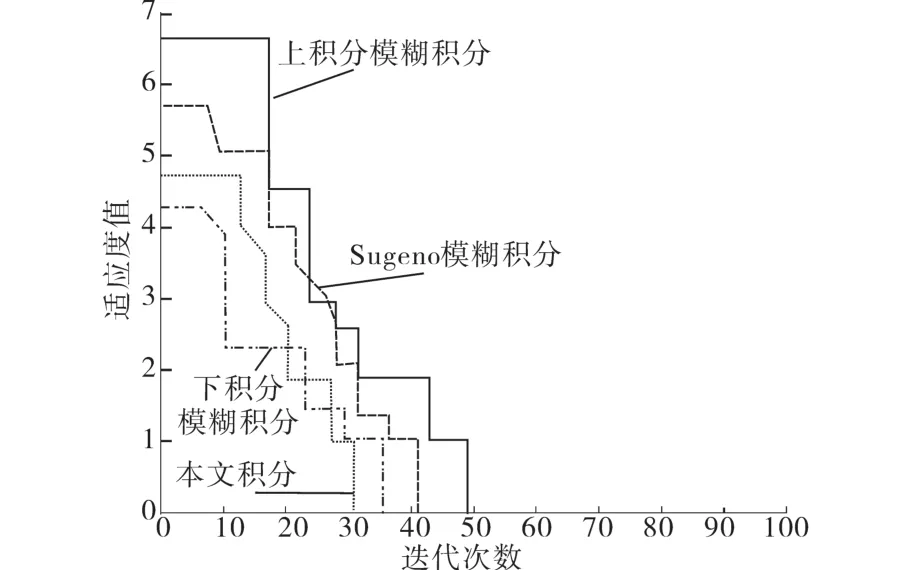
图2 仿真结果Fig.2 Simulation results

从图2结果可以看出，当4种模糊积分均达到收敛的情况下，本文采用的模糊积分相比较其它3种模糊积分方法，达到全局最优的迭代次数最小。对该4种模糊积分方法各自运行100次，按照每次进行故障定位得到最优解的迭代次数，对消耗时间的最大值、最小值、均值以及正确率进行记录。表3为不同模糊积分方法对配电网故障区域的定位结果。

表3 故障区域的定位结果Tab.3 Location results of fault area

表3数据说明，本文模型在利用Choquet模糊积分进行配电网故障区域定位时，迭代次数的最大值都远低于其它模糊积分的迭代次数，且消耗时间也较短，节约了大量的时间资源，故障定位的准确率比其它模糊积分高10%以上。可见本文模型采用的Choquet模糊积分在进行搜索配电网的故障发生位置时，可快速、准确地定位故障发生的准确位置。

实验在Matlab仿真环境下，监测本文基于大数据的配电网故障诊断预测模型进行故障检测时配电网的生命周期和安全性。实验模拟仿真100个故障发生点，将每个故障点视为一个节点，将中性点不接地单向接地故障检测模型、基于无线传感器的故障检测模型当成对比模型，三种故障检测手段分别对100个实验配电网故障点进行检测。

图3为不同检测时间下，实验配电网在不同模型下的生命周期图像。

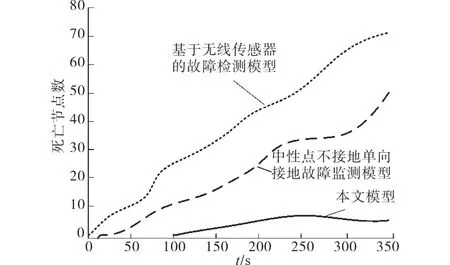
图3 配电网的生命周期图像Fig.3 Life cycle image of distribution network

从图3生命周期图像可以看出，进行故障检测后很多故障发生位置的数据失效节点死亡，本文模型相较与其它两种模型其在故障检测过程中死亡节点在10%以内，另外两种模型在故障检测后节点失效比例较高，说明本文模型提高了配电网的生命周期，提高大规模配电网的使用期限和经济效益。

在对配电网进行故障检测中干扰数据会对故障点的准确判断造成影响，故障节点接收的干扰数据越少，检测出的故障点的可信度就越高。实验对三种故障检测模型在不同时间下接收的干扰数据进行测量，测量接收干扰数据比例结果如图4所示。

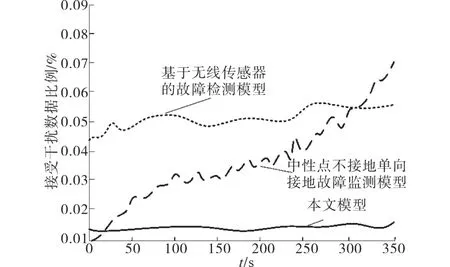
图4 故障点接收干扰数据比例Fig.4 Proportion of interference data received at the fault point

从图4结果可以看出，本文模型在进行故障诊断时随着时间增长，接收的干扰数据比例较低，保持在0.01%～0.02%之间；而中性点不接地单向接地故障检测模型从故障检测开始接收的干扰数据比例就不断上升，对故障诊断造成的影响较大；基于无线传感器的故障检测模型虽然随时间变化接收干扰数据比例波动较小，但基数值较大，对配电网的故障诊断误判影响也较大。说明本文模型在应用于较大规模的配电网故障诊断时，接收干扰数据较低，故障诊断正确率较高。

3 结论

本文设计的基于大数据的配电网故障诊断预测模型，首先采用RS-IA模型对大规模故障信息进行智能搜索，计算出最优约简得到决策规则，实现对配电网故障发生位置的初步定位；再采用基于模糊积分的故障诊断预测模型，根据初步诊断结果确定发生故障的候选元件及模糊测度值；最后确定配电网故障发生的准确位置。结果表明，本文设计的模型在应用于较大规模的配电网故障诊断时，能对大规模配电网故障进行准确定位，缩短故障检测用时，提高时间的利用效率，并且接收干扰数据较低，故障诊断正确率较高，延长了配电网的使用期限。