非理想电网下三相逆变器的锁相方法研究

阮鹏 ，吴赵风，田刚领，黄雁，吕建国，刘钊

（1.平高集团有限公司，河南 平顶山 467001；2.南京理工大学自动化学院，江苏 南京 210094）

随着智能电网和微电网技术的快速发展，新能源并网逆变器作为新能源分布式发电单元和电网的接口单元，其优良的工作性能对保证电力系统的稳定运行至关重要。三相并网逆变器需具有在三相不平衡、谐波污染、频率突变等非理想电网环境下运行的能力。通常，三相电网不平衡表现为电网电压中含有基波负序及零序分量；谐波污染表现为电网电压中含有5次、7次及少量高次谐波分量；电网频率突变是指电网电压的频率波动及闪变。因此，如何在非理想电网条件下快速准确地检测电网电压的频率、相位等信息成为了并网逆变器高效、稳定运行的关键问题之一[1]。

在理想电网下，三相并网逆变器一般采用单同步坐标系锁相环（synchronous rotating frame phase-locked loop，SRF-PLL）对电网电压的相位、频率等信息同步检测。然而，在非理想电网下，因受到基波负序分量及谐波分量的影响，锁相环检测的信息与真实电网信息存在误差[2-3]。为有效解决不平衡电网下SRF-PLL输出频率、相位波动的问题，文献[4]提出了基于双同步坐标系解耦的锁相环（decoupled double synchronous reference-frame PLL，DDSRF-PLL），该方法在不平衡电网下准确检测电网电压的相位、频率、幅值等信息；但是在谐波电网条件下，因谐波信号不是对称存在的，双同步坐标系软件锁相环的解耦结构并不能有效地滤除谐波对锁相环的影响。因而，在谐波电网条件下，DDSRF-PLL输出的频率、相位信息存在误差。文献[5]在双同步坐标系下增加低通滤波器以减少电网谐波对锁相环的影响，从而达到减小锁相误差的目的，但该低通滤波器的加入将导致锁相环带宽变窄，影响锁相环动态性能。文献[6]提出了基于双二阶广义积分器的锁相环（dou⁃ble second-order generalized integrator PLL，DSO⁃GI-PLL）。在不对称电网条件下，DSOGI-PLL可以快速准确检测出电网电压相位、频率等信息，但是，当电网电压含大量低次谐波时，由于双二阶广义积分器对电网电压低次谐波分量的滤波效果不足，锁相环输出信息将存在误差。文献[7]针对不平衡谐波电网，提出了基于改进全通滤波器的DSOGI-PLL方法，提高了锁相环的性能。

文献[8]提出基于延时信号消除法的锁相环（delayed signal cancellation PLL，DSC-PLL）。单个延时信号消除模块可以滤除电网电压信号中特定次谐波分量，若级联多个不同延时信号消除模块可以滤除电网电压信号中多种谐波分量及基波负序分量[9]。文献[10-11]针对延时信号消除模块，利用坐标变换的方式，将其从旋转坐标系转换到两相静止坐标系（α-β坐标系）下，此时，谐波信号频率相对较高，所需滤波器滤波窗口时间较窄，从而减少滤波窗口总时间，达到了改善滤波速度的目的。文献[12]对基于延时信号消除法的锁相环进行了分析，并提出采用比例-积分-微分（ proportional-integral-derivative，PID）控制器替代比例-积分（proportional-integral，PI）控制器，提高该锁相环的动态响应速度。虽然DSC-PLL可以准确快速检测出非理想电网信息，但由于引入延时信号消除模块，系统闭环模型需要重新分析建立，且其参数设计变得较为复杂。文献[13-14]对延时信号消除法进行了详细分析，并研究了该方法的离散化实现，减少其计算量。文献[15]提出基于广义延时信号消除法的锁相环（general⁃ized delayed signal cancellation PLL，GDSC-PLL）。GDSC-PLL可在α-β坐标系下提取电网电压基波正序分量，从而减小对锁相环相位裕度的影响，但其结构和离散化实现比较复杂。文献[16]提出了在两相旋转坐标系（d-q坐标系）下的基于滑动平均滤波器的锁相环（moving average filter PLL，MAF-PLL）。文献[17-18]对MAF-PLL进行了详细的分析，并对该锁相环进行了相位补偿设计。但是，在d-q坐标系下，由于加入了MAF，使得PLL带宽变窄，动态性能有待提高。文献[19]结合了DSC-PLL和MAF-PLL两种锁相环，进行了相位补偿和相位误差前馈设计，从而改善了锁相环动态性能。

上述锁相环的研究主要针对非理想电网中基波负序分量及谐波分量带来的锁相环跟踪误差、动态性能等问题，并提出了解决方法。为了有效滤除谐波，需要折中考虑滤波器带宽、锁相环动态响应速度，这将影响锁相环稳态跟踪误差，所提出的锁相环的设计方法与实现过程也相对复杂。

因此，本文提出基于新型滑动平均滤波器的锁相环（novel moving average filter PLL，NMAFPLL）方法。针对非理想电网条件，在α-β坐标系下，NMAF-PLL完成了电网电压的基波正序分量提取，合理减少窗口采样点数，从而减少了在线计算量，同时缩短了滤波窗口时间，改善了锁相环的动态性能。进一步，采用双锁相环结构，实现了NMAF-PLL对电网频率突变的自适应跟踪功能，有效地减小了锁相误差。仿真与实验结果表明，在非理想电网下，所提出的NMAF-PLL方法具有良好的动态与稳态性能。

1 新型滑动平均滤波器的基本原理

滑动平均滤波器（MAF）的传递函数[17]为

式中：Tw为滤波窗口时间。

通过零极点偏移可得新型滑动平均滤波器（NMAF）的传递函数为

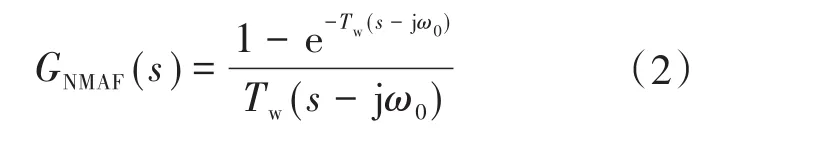
式中：ω0为中心额定角频率。

将s=jω代入式（2）中，可得NMAF的频率响应方程为

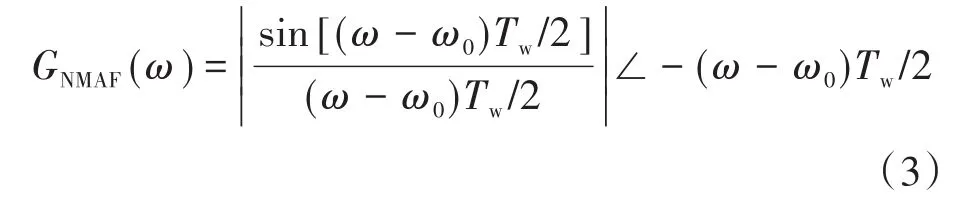
当ω0取值为100π rad/s，Tw取值为0.02 s时，根据式（3）得到NMAF的幅频特性曲线及相频特性曲线，如图1所示。从图中可以看出，NMAF能够完全滤除输入信号中的零序分量、基波负序分量、5次谐波分量、7次谐波分量等。

图1 NMAF的伯德图Fig.1 Bode diagram of NMAF

为了在数字控制系统中实现NMAF，首先将其离散化，通常采用带零阶保持器的离散化方法对NMAF进行离散化设计[17]，其Z变换离散公式为

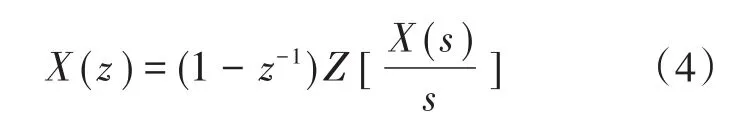
其中，（1-z-1）Z[1/s]为零阶保持器的Z变换形式，Z表示Z变换。

根据式（2）和式（4），推导得到NMAF的z域传递函数为

式中：N为滤波窗口时间内的取样点个数。

进一步，假设Ts为数字控制系统的采样周期，由式（5）可推导出NMAF对基波正序信号提取的离散表达式为

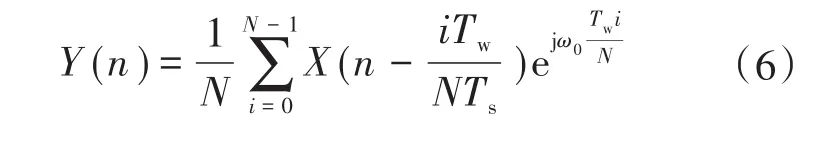
2 α-β坐标系下NMAF-PLL设计

在实际非理想电网下，电网电压主要含有零序分量、基波分量、5次谐波、7次谐波及少量高次谐波分量。其中，基波分量主要包括基波正序分量和基波负序分量；由于高次谐波分量含量较少，锁相环受其影响较小，此处忽略不计。三相电网电压经Clark变换，在两相静止坐标系（α-β坐标系）下可以表示成下式：

根据新型滑动平均滤波器的基本思想，本文提出新型滑动平均滤波器的锁相环（NMAF-PLL）方法。该方法在两相静止坐标系（α-β坐标系）下，采用新型滑动平均滤波器提取电网电压基波正序分量，锁定电网电压的频率、相位，其结构框图如图2所示。

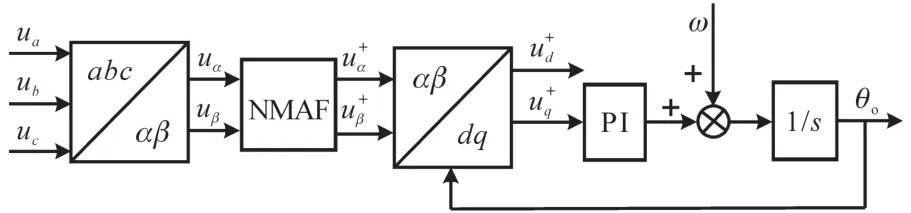
图2 NMAF-PLL结构框图Fig.2 Structure diagram of NMAF-PLL

为了便于所提的NMAF-PLL方法的数字实现，在保持其在连续域中幅频特性的基础上，进一步简化离散化处理。当N值较大时，计算量过大，数字实现较为困难。而在非理想电网下，电网电压的谐波分量主要包含5次谐波和7次谐波分量等。通过合理减小N值，可以达到滤除5次、7次谐波等分量，同时减小计算量的目的。分析可知，当N取5时，NMAF可以完成对非理想电网电压中基波正序分量的提取。

由式（5）可得简化NMAF的z域传递函数为

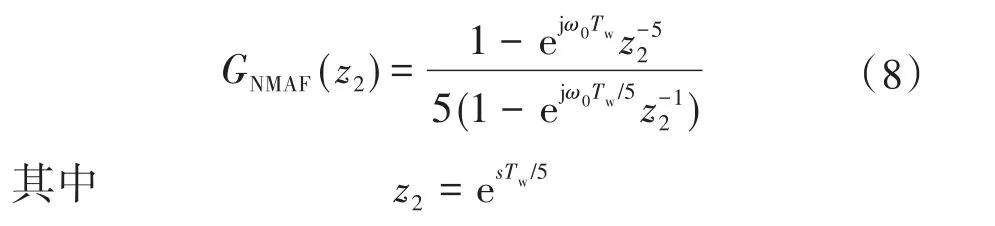
根据式（8），作出简化后NMAF的伯德图，如图3所示。从图中分析可知，在非理想电网下，当电网额定工频频率为50 Hz，Tw取值为0.02 s时，NMAF可以有效地滤除电网电压中的零序分量、基波负序分量、5次谐波分量以及7次谐波分量等。

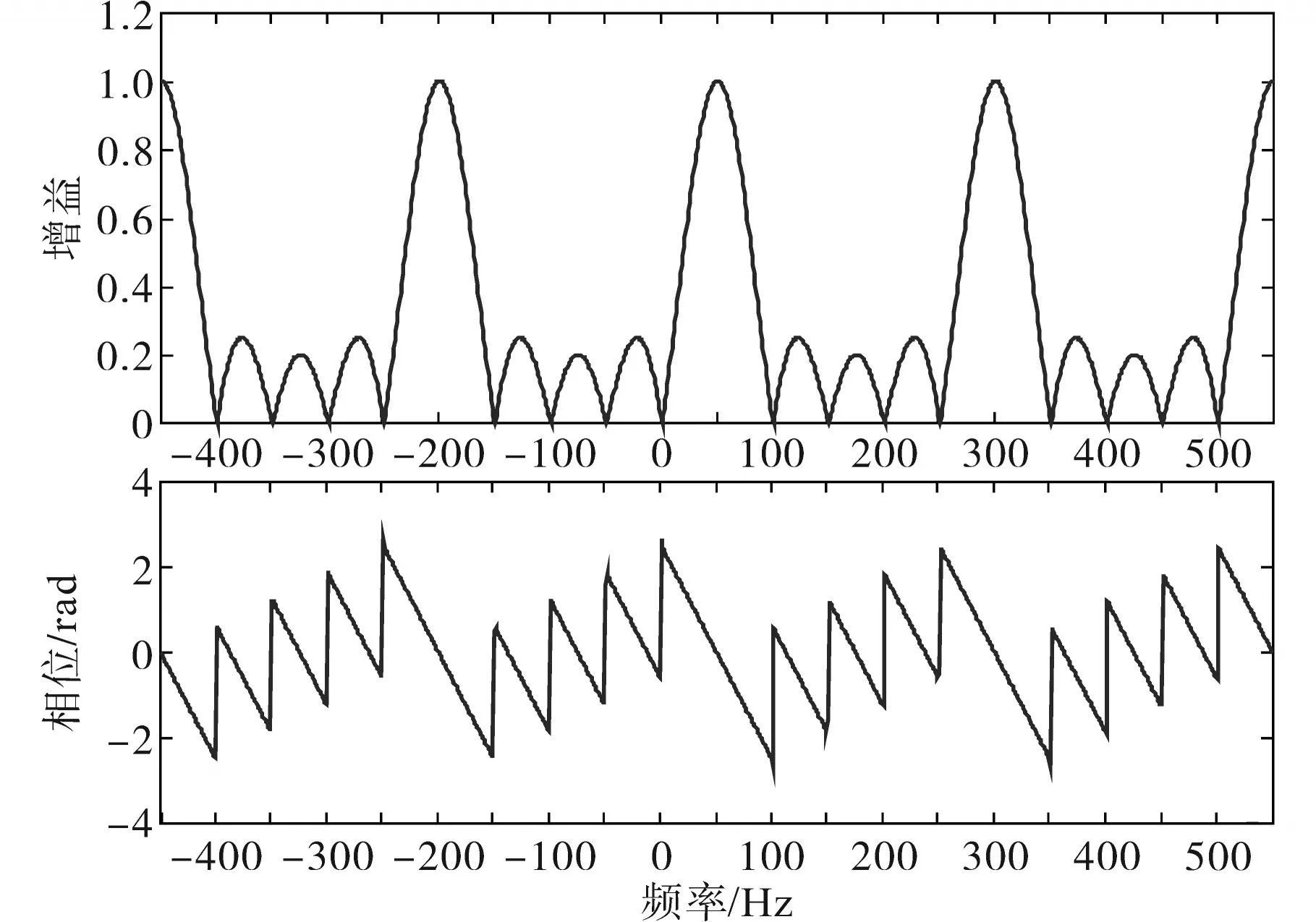
图3 简化的NMAF伯德图Fig.3 Bode diagram of simplified NMAF

简化后，根据式（6），运用旋转矩阵[15]，NMAF在α-β坐标系下完成对基波正序信号提取的数字实现表达式为

当电网发生频率突变时，由于NMAF的滤波窗口时间为固定值，滤波器无法完全滤除干扰信号，从而导致NMAF-PLL产生锁相误差。因此，通过自适应跟踪电网频率突变，根据真实电网电压周期值，实时调整NMAF滤波窗口时间，从而可以有效滤除干扰信号，减小锁相环的输出误差。

通常，为实现锁相环对电网频率的自适应跟踪，若采用锁相环自身的频率输出直接前馈给NMAF，这将导致锁相环进入稳态的调节时间难以确定[15]，直接影响并网逆变器的动态性能。

这里，文中采用双锁相结构实现了锁相环对电网频率自适应跟踪，以减小锁相环的输出稳态误差。该NMAF-PLL锁相方法的内部结构如图4a所示。其中，NMAF1-PLL和NMAF2-PLL分别如图4b和图4c所示。

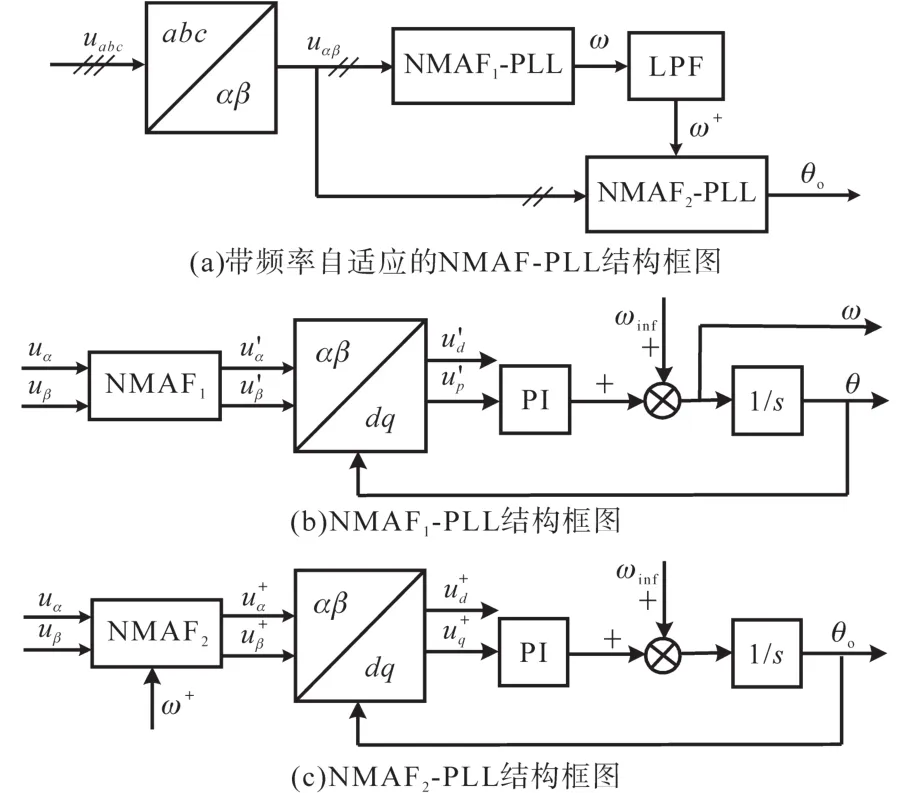
图4 NMAF-PLL的内部结构框图Fig.4 Internal structure block diagram of NMAF-PLL

如图4a所示，NMAF1-PLL获得的频率信号经低通滤波器（low-pass filter，LPF）得到当前电网频率信号ω+；进一步，NMAF2-PLL获得NMAF1-PLL输出的ω+，根据电网频率信号ω+，实时计算出自适应滑动滤波器的滤波窗口时间：

从而，NMAF2-PLL实现了在电网频率突变时，快速跟踪电网频率变化，减小锁相环对电网电压相位的跟踪误差，提高锁相环的动态性能。

根据式（8），图4a带频率自适应的NMAF-PLL锁相方法的等效传递函数表示为

最后，根据式（9）可以推导得出带频率自适应的NMAF-PLL锁相方法在α-β坐标系下完成对基波正序信号提取的数字实现表达式为

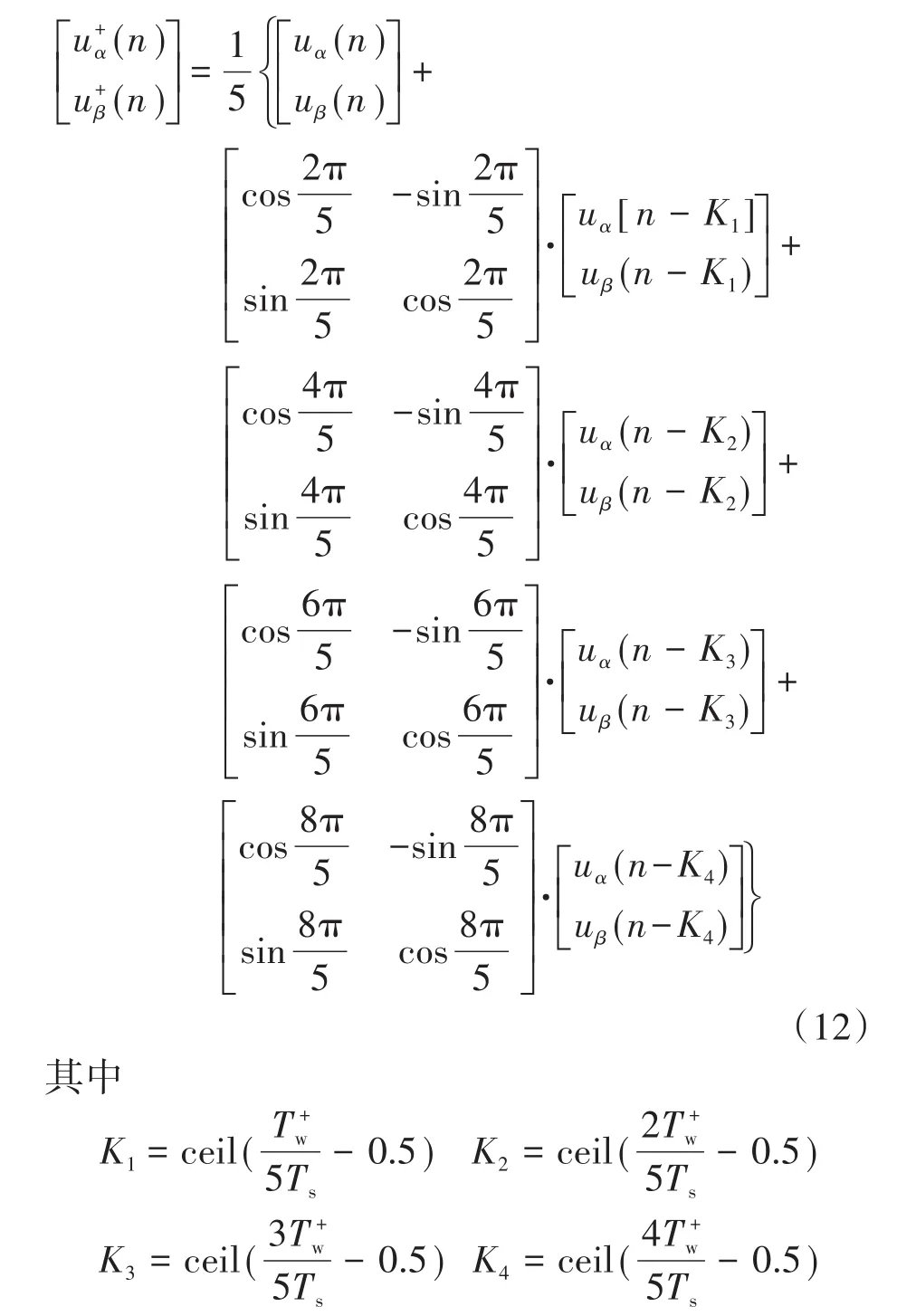
综上，为了数字实现图4a的带频率自适应的NMAF-PLL锁相方法，在数字系统中采样周期Ts内，NMAF1-PLL中滑动平均滤波器NMAF1采用式（9）实现；NMAF2采用式（12）实现。

3 仿真验证

为了有效验证NMAF-PLL锁相方法在并网逆变器系统中的实际效果，文中搭建了NPC三电平并网逆变器的仿真模型，采用比例积分-准谐振控制器实现非理想电网下的并网电流控制。在三相电网电压不对称、谐波污染、电压频率突变的非理想情况下进行仿真验证。主要仿真参数如下：额定三相电压基波幅值U=50 V，额定三相电压基波角频率ω=314 rad/s，三相电压工频周期Tw=0.02 s，锁相环内PI控制器kp=2.5，ki=159，采样周期Ts=50 μs。

为了对比分析文中所提NMAF-PLL锁相方法的有效性，这里选择了DSOGI-PLL锁相方法进行对比仿真验证。在电网不平衡、电网不平衡伴随谐波干扰、电网频率突变伴随谐波污染条件下的仿真结果如图5所示。其中，图5a中a相电压不变，b相跌落20%，c相跌落50%；图5b中a相电压不变，b相跌落20%，c相跌落50%，同时向电网中注入10%的负序5次谐波和10%的正序7次谐波；图5c中电网频率由314 rad/s突变至282 rad/s，同时向电网中注入10%的负序5次谐波和10%的正序7次谐波。

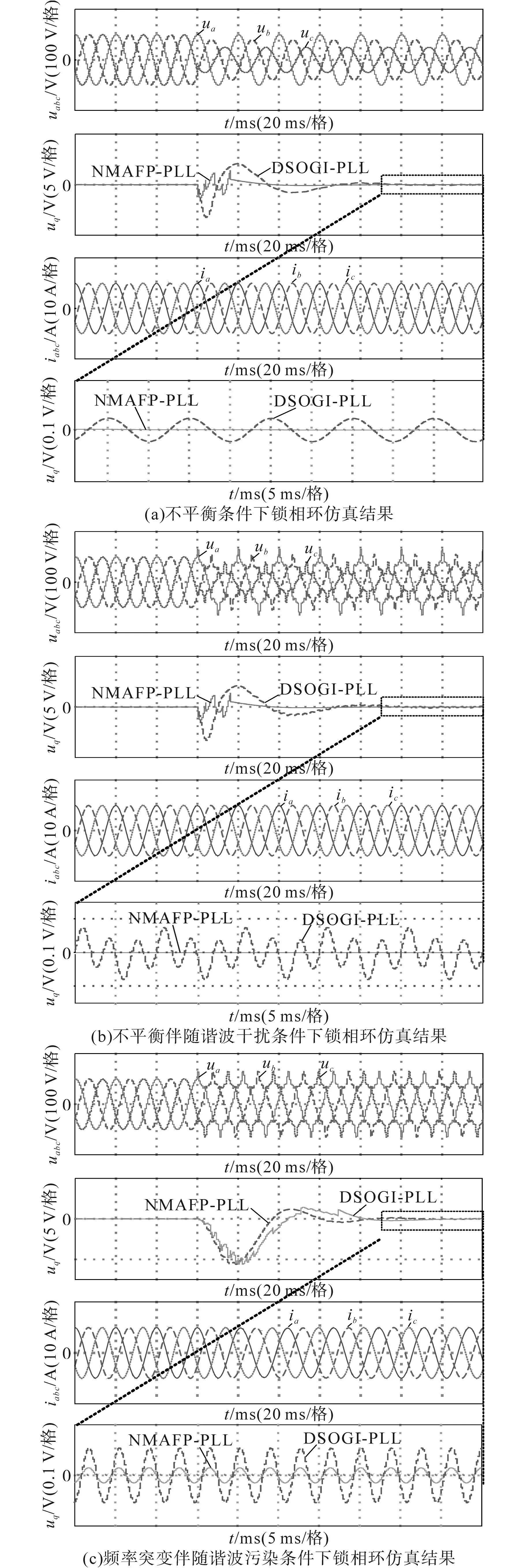
图5 非理想电网下锁相环仿真结果Fig.5 Simulation results with non-ideal grid conditions

在图5中，通过锁相环输出q轴电压波形分析锁相环的性能，图中分别给出了NMAF-PLL和DSOGI-PLL两种锁相环的q轴电压值。通过对比仿真结果中的q轴电压值变化情况可知，在电网不平衡、电网不平衡伴随谐波干扰两种条件下，文中所提NMAF-PLL锁相方法在2个工频周期内达到稳定的锁相输出状态；在频率突变伴随谐波干扰电网条件下，文中所提NMAF-PLL锁相方法在5个工频周期内达到稳定的锁相输出状态。

因此，相对于DSOGI-PLL锁相方法，文中所提出的NMAF-PLL锁相方法可以更快地进入稳态，整体动态调节时间更短，且在电网谐波污染时锁相环的稳态特性更好。

为了进一步分析所提出的NMAF-PLL锁相方法的效果，这里选择了三种典型的锁相方法进行仿真对比分析。三种方法分别是：文献[4]的DDSRF-PLL方法、文献[15]的GDSC-PLL方法和文献[16]的MAF-PLL方法，仿真结果如图6所示。详细的对比分析结果如表1所示。

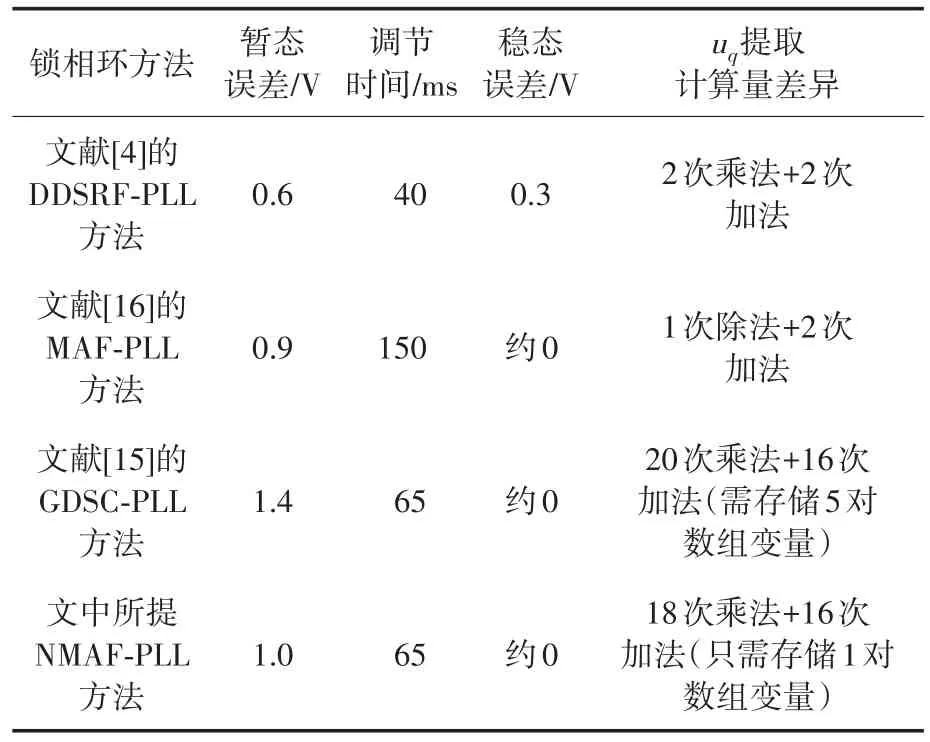
表1 上述锁相环的对比仿真结果Tab.1 Simulation results comparison for the above PLL methods

由图6可知，与文献[4]的DDSRF-PLL方法、文献[16]的MAF-PLL方法相比，文中所提NMAFPLL方法能够兼顾实现锁相环的动态调节时间短和稳态锁相误差小。从图6a可以看出，与文献[15]的GDSC-PLL方法相比，文中所提NMAF-PLL方法同样具有较好的动态调节速度和稳态性能；但是在动态调节过程中，文中所提方法的暂态波动更小。同时，从锁相环的内部结构、离散化数字实现上看，与文献[15]的GDSC-PLL方法相比，文中NMAF-PLL方法的计算量相对减小，且数字控制周期内存储的数组变量的数量较少。

图6 锁相环对比仿真结果Fig.6 Simulation results comparison for different PLL methods

综上所述，文中所提NMAF-PLL方法能够兼顾锁相环动态调节过程中较小暂态误差的同时，实现了锁相环在非理想电网下动态调节时间短、锁相稳态误差小的目标。

4 实验验证

为了有效验证锁相环在并网逆变器运行中的实际效果，文中搭建了NPC三电平并网逆变器实验平台，实验结果如图7所示。实验采用两台NPC三电平并网逆变器，其中一台逆变器模拟非理想电网，另一台逆变器作为被试并网逆变器，用来验证锁相环特性。实验参数条件与仿真参数一致，数字控制系统采用DSP28377D作为核心处理器，为了便于观察锁相环相位信息，其输出的q轴电压值由D/A输出，可以分析锁相环运行状况。

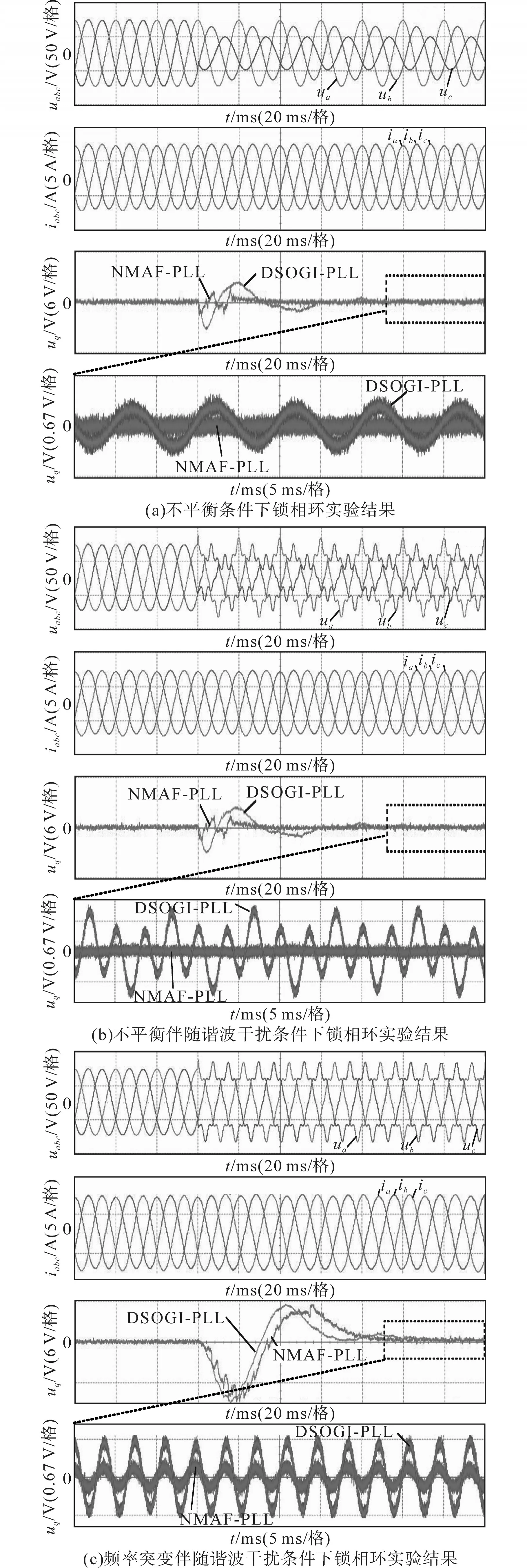
图7 非理想电网下锁相环实验结果Fig.7 Experimental results with non-ideal grid conditions

图7是在电网不平衡、不平衡伴随谐波畸变、频率突变伴随谐波干扰三种非理想电网情况下，电网电压、锁相环输出特性以及NPC三电平并网逆变器并网电流的实验波形。图7a为电网电压不平衡时并网逆变器的实验波形，图7b为电网电压不平衡同时存在谐波干扰时NPC三电平并网逆变器的实验波形，图7c为电网电压发生频率突变同时存在谐波干扰时NPC三电平并网逆变器的实验波形。由实验结果可以看出，在非理想电网下，相比于DSOGI-PLL锁相方法，文中所提出的NMAF-PLL锁相方法能够更快地恢复稳定，具有更好的动态和稳态性能。

5 结论

为解决非理想电网下并网逆变器的锁相问题，文中提出了带频率自适应功能的NMAF-PLL锁相方法。

该方法基于新型滑动平均滤波器，在α-β坐标系下实现了对三相电网电压的基波正序信号的快速提取，有效滤除了电网基波负序分量、低次谐波分量。进一步，采用双锁相结构，能够自适应跟踪电网电压频率突变，实时计算滤波器窗口取样数，从而减小了电网相位跟踪误差，并提高了锁相环的动态性能。仿真和实验结果表明，在非理想电网下，文中所提出的NMAF-PLL锁相方法能够兼顾锁相环动态调节过程中较小暂态误差的同时，实现了动态调节时间短、锁相稳态误差小的目标，该锁相方法具有良好的稳态和动态性能。