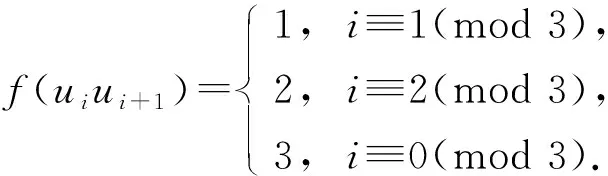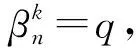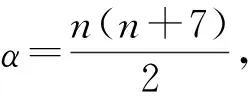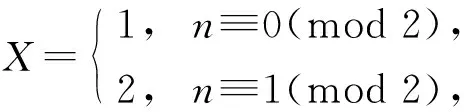联图的邻点全和可区别全染色
2022-01-21崔福祥叶宏波
崔福祥, 杨 超, 叶宏波, 姚 兵
(1. 上海工程技术大学 数理与统计学院, 智能计算与应用统计研究中心, 上海 201620; 2. 西北师范大学 数学与统计学院, 兰州 730070)
1 引言与预备知识

定义1设f:V(G)∪E(G)→{1,2,…,k}是图G的一个正常k-全染色.令权值

其中N(x)={y∈V(G)|xy∈E(G)}.对任意的边uv∈E(G), 如果φ(u)≠φ(v)成立, 则称f是图G的一个邻点全和可区别k-全染色.图G的邻点全和可区别全染色中最少的颜色数称为G的邻点全和可区别全色数, 记为ftndi∑(G).
定义2设图Gm,Gn为互不相交的简单连通图, 若其同时满足如下两个条件:
1)V(Gm∨Gn)=V(Gm)∪V(Gn);
2)E(Gm∨Gn)=E(Gm)∪E(Gn)∪{uv|u∈V(Gm),v∈V(Gn)}.
则称图Gm∨Gn为Gm和Gn的联图.
设V(Gm)={ui|1≤i≤m},V(Gn)={vj|1≤j≤n}.由联图Gm∨Gn的定义知, 要验证一个正常全染色f为Gm∨Gn的一个邻点全和可区别全染色, 需下述3个条件同时成立:
(i)φ(ui)≠φ(ui+1), 1≤i≤m-1;
(ii)φ(vj)≠φ(vj+1), 1≤j≤n-1;
(iii)φ(ui)≠φ(vj), 1≤i≤m, 1≤j≤n.

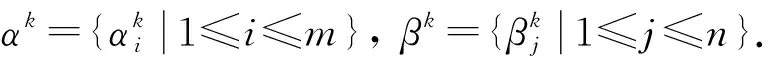
本文确定了路与路、 路与圈、 圈与圈三类联图的邻点全和可区别全色数.
2 主要结果
由定义1和定义2知, 图G的一个邻点全和可区别全染色也是图G的一个正常全染色, 从而有:
引理1设G是一个阶数至少为3 的简单连通图, 则ftndi∑(G)≥Δ(G)+1.
定理1设Pm和Pn分别表示阶数为m和n的两条路(m≥n≥3), 则当m=n时, ftndi∑(Pm∨Pn)≤Δ+2, 当m≠n时, ftndi∑(Pm∨Pn)=Δ+1.
证明: 设路Pm=u1u2…um, 路Pn=v1v2…vn.下面分两种情形讨论.
情形1) 当m=n时, 定义Pm∨Pn的一个(Δ+2)-全染色f1如下:
联边uivj的染色f1(uivj)由下列边染色矩阵确定:
其中i∈[1,m],j∈[1,n].
①n≡1(mod 2).
由染色f1, 易知Φ(ui)={8,9,13,14},Φ(vj)={6,7,11,12}.显然, 连通分支Pm中的相邻顶点以及连通分支Pn中的相邻顶点的权值都是可区别的, 因此下面只需证联图G中相邻顶点ui和vj的权值不同即可.因为


故当n>3时,φ(ui)<φ(vj).当n=3时, 保持上述染色方案不变, 经验证也满足G中相邻顶点ui与vj的权值不同.故ftndi∑(Pm∨Pn)≤Δ+2.
②n≡0(mod 2).
由染色f1可得Φ(ui)={8,13,14},Φ(vj)={6,11,12}.显然, 在连通分支Pm中的相邻顶点和Pn中的相邻顶点的权值都是可区别的, 因此下面只需证联图G中相邻顶点可区别即可.因为


故当n>4时,φ(ui)<φ(vj).当n=4时, 调整分支Pn的边染色, 使得f(v1v2)=f(v3v4)=4,f(v2v3)=3, 则可得G中相邻顶点ui与vj的权重不同, 从而可得ftndi∑(Pm∨Pn)≤Δ+2.
情形2) 当m>n时, 定义Pm∨Pn的一个(Δ+1)-全染色f2如下:
联边uivj的染色f2(uivj)由下列边染色矩阵确定:
其中i∈[1,m],j∈[1,n].

αk={p-k,p-2k,…,p-nk,p+n(1-k),p+n(2-k),…,p},
且αk中的元素满足

① 计算路Pm中各顶点的权值φ′(ui)和φ(ui):
φ′(u1)=12,φ′(um-1)=2m+12.



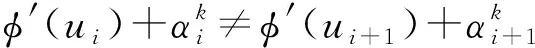
可得k=9, 即当m=n+9时,φ(u1)=φ(u2).当2≤i≤m-2时, 若i=n, 此时当n≤m-3时, 若φ(un)=φ(un+1), 则
无解; 当n=m-2时, 若φ(un)=φ(un+1), 则由
得m=n+3, 即当m=n+3时,φ(um-1)=φ(um-2).若i 可得n=m+4(或m+3)>m, 矛盾. 综上可知, 对于路Pm中任意相邻顶点ui和ui+1, 均有φ(ui)≠φ(ui+1), 且max{φ(ui)}=φ(um-2)(或φ(um-1)). ② 计算路Pn中各顶点的权值φ(vj): φ(v1)=φ(vn)=6+2β. 当2≤j≤n-1时, 显然, 对于路Pn中任意相邻顶点vj和vj+1, 均有φ(vj)≠φ(vj+1), 且min{φ(vj)}=6+2β. 当m≥4时, 有m2-3m>0, 故对任意的ui∈V(Pm),vj∈V(Pn), 均有φ(ui)<φ(vj).当max{φ(ui)}=φ(um-1)时有 当m≥4时, 有m2-m-6>0, 故对任意的ui∈V(Pm),vj∈V(Pn), 均有φ(ui)<φ(vj). 综上可知, 对任意顶点ui∈V(Pm),vj∈V(Pn), 均有φ(ui)≠φ(vj).证毕. 定理2设Pm和Cn分别表示阶数为m和n的路和圈(m,n≥3), 则 且当m=n≠1(mod 2) 时, ftndi∑(Pm∨Cn)≤Δ+2. 证明: 设路Pm=u1u2…um, 圈Cn=v1v2…vnv1, 则Pm∨Cn=Pm∨Pn∪{v1vn}.下面分3种情形讨论. 情形1) 当m=n≠1(mod 2) 时, 定义Pm∨Cn的一个(Δ+2)-全染色g1如下: g1(v1vn)=4; g1(uivj)=f1(uivj), 1≤i≤m, 1≤j≤n; g1(x)=f1(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}. 由染色g1得Φ(ui)={8,13,14},Φ(vj)={11,12}.显然, 在连通分支Pm中相邻顶点和Cn中相邻顶点的权重都是邻和可区别的, 因此下面仅需证联图G中相邻顶点ui与vj的权值不同即可.又因为 所以当n≥3时,φ(ui)<φ(vj), 故ftndi∑(Pm∨Cn)≤Δ+2. 情形2) 当m>n且n≠1(mod 3)时, 定义Pm∨Cn的一个(Δ+1)-全染色g2如下: g2(v1vn)=m+3; g2(uivj)=f2(uivj), 1≤i≤m, 1≤j≤n; g2(x)=f2(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}. ① 路Pm中各顶点的权值φ′(ui)和φ(ui)同定理1中情形2)的①. ② 计算圈Cn中各顶点权值φ(vj): φ(vn)=m+10+2β. 当2≤j≤n-1时,φ(vj)同定理1中情形2)的②.显然, 对于圈Cn中任意相邻顶点均有φ(vj)≠φ(vj+1), 且min{φ(vj)}=9+2β. 当n≥3时, 有m2-3m+6>0.故对任意顶点ui∈V(Pm),vj∈V(Cn), 均有φ(ui)≠φ(vj).当max{φ(ui)}=φ(um-1)时, 有 当n≥3时, 有m2-m>0.故对任意顶点ui∈V(Pm),vj∈V(Cn), 均有φ(ui)≠φ(vj). 综上可知, ftndi∑(Pm∨Cn)=Δ+1. 情形3) 当m 联边uivj的染色g3(uivj)由下列边染色矩阵确定: 其中i∈[1,m],j∈[1,n]. βk={q-k,q-2k,…,q-mk,q+m(1-k),q+m(2-k),…,q}, 且集合中元素满足 ① 计算路Pm中各顶点权值φ(ui): φ(u1)=φ(um)=6+2α. 当2≤i≤m-1时, 显然, 对于路Pm中任意相邻顶点均有φ(ui)≠φ(ui+1), 且min{φ(ui)}=6+2α. ② 计算圈Cn中各顶点权值φ′(vj)和φ(vj): φ′(v1)=n+19,φ′(vn-1)=2n+12. 可得m=2n-2, 又m 无解; 当m=n-2时, 若φ(vm)=φ(vm+1), 则由 得n=m+3, 即当n=m+3时,φ(vm)=φ(um+1).若j 综上可知, 对于圈Cn中任意相邻顶点vi和vj+1, 均有φ(vj)≠φ(vj+1), 且有max{φ(vj)}=φ(vn-2)(或φ(vn)). 当n≥4时, 有n2-n-4>0, 故对任意ui∈V(Pm),vj∈V(Cn), 均有φ(ui)<φ(vj). 当max{φ(vj)}=φ(vn-2)时, 有 故对任意ui∈V(Pm),vj∈V(Cn), 均有φ(ui)<φ(vj). 综上可知, 对任意顶点ui∈V(Pm),vj∈V(Cn), 均有φ(ui)≠φ(vj).证毕. 定理3设Cm和Cn分别表示阶数为m和n的两个圈(m≥n≥3), 则 且当m=n≠1(mod 2)时, ftndi∑(Cm∨Cn)≤Δ+2. 证明: 设圈Cm=u1u2…umu1, 圈Cn=v1v2…vnv1, 则Cm∨Cn=Pm∨Pn∪{u1um,v1vn}.下面分两种情形讨论. 情形1) 当m=n≠1(mod 2)时, 定义Cm∨Cn的一个(Δ+2)-全染色h1如下: h1(u1um)=2; h1(v1vn)=4; h1(uivj)=f1(uivj), 1≤i≤m, 1≤j≤n; h1(x)=f1(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}. 由染色h1可得Φ(ui)={13,14},Φ(vj)={9,10}.显然, 连通分支Cm中的相邻顶点以及连通分支Cn中的相邻顶点的权值都是可区别的, 因此下面只需证联图G中相邻顶点ui与vj的权值不同即可.又因为 故当n≥4时,φ(ui)<φ(vj), 即ftndi∑(Cm∨Cn)≤Δ+2. 情形2) 当m>n且n≠1(mod 3)时, 定义Cm∨Cn的一个(Δ+1)-全染色h2如下: h2(u1um)=h2(v1vn)=m+3; h2(uivj)=f2(uivj), 1≤i≤m, 1≤j≤n; h2(x)=f2(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}. ① 计算圈Cm中各顶点权值φ′(ui)和φ(ui): φ′(u1)=m+19. 可得m<2, 矛盾.故φ(u1)≠φ(u2).当2≤i≤m-2时,φ′(ui)和φ(ui)同定理1的情形2)中2≤i≤m-2的情形.若φ(um-1)=φ(um), 则由 得n<0, 矛盾.若φ(um)=φ(u1), 则由 可得m<3(或m<2), 矛盾. 与上述证明过程类似, 当m=n+3时, 调整染色方案, 令 经验证调整后的染色是Cm∨Cn的一个邻点全和可区别全染色. 综上可知, 对于圈Cm中任意相邻顶点ux,uy, 均有φ(ux)≠φ(uy), 且max{φ(ui)}=φ(um-2)(或φ(um)). ② 计算圈Cn中各顶点权值φ(vj): 当2≤j≤n-1时,φ(vj)同定理1中情形2)的②.显然, 对于圈Cn中任意相邻顶点vx,vy, 均有φ(vx)≠φ(vy), 且min{φ(vj)}=9+2β. 当m≥4时, 有m2-3m+6>0.故对任意的ui∈V(Cm),vj∈V(Cn), 均有φ(ui)≠φ(vj).当max{φ(ui)}=φ(um)时, 有 当m≥4时, 有m2-m-10>0, 故对任意的ui∈V(Cm),vj∈V(Cn), 均有φ(ui)≠φ(vj). 综上可知, ftndi∑(Cm∨Cn)=Δ+1.证毕.