6°攻角尖锥高超声速边界层高频不稳定波实验研究

刘姝怡，陈坚强,*，袁先旭，熊有德，吴 杰

1.空气动力学国家重点实验室，四川 绵阳 621000；2.华中科技大学 航空航天学院，武汉 430074

0 引 言

高超声速飞行器表面流动为湍流状态时，表面摩擦力和热流显著大于层流，导致表面温度过高甚至损坏隔热材料，影响飞行器稳定飞行。因此，认识高超声速边界层从层流转捩为湍流的机理对未来飞行器设计至关重要。

第二模态不稳定波在高超声速边界层转捩中有着重要作用[1-2]。Li 等[3]在HIFiRE-1 飞行试验中研究发现0°攻角下圆锥转捩的主导机制是第二模态。李存标[4]和张传鸿[5]等通过实验研究发现，转捩后期第二模态波被抑制，并在转捩前出现一段安静区。陈坚强等[6]通过动态模态分解获得各模态的空间相对位置，发现线性阶段第二模态占优，转捩后期低频模态占优，且二者之间存在模态转换。

在有攻角情况下，边界层具有三维特性，转捩过程变得更为复杂。与0°攻角情况相比，圆锥转捩位置在迎风面推迟，在背风面提前。Stetson 等[7]总结了高超声速边界层实验研究成果，得出了“小攻角对第二模态增长率影响较小，大攻角的影响与第二模态扰动增长的起始位置有关”的结论。Berridge[8]通过实验研究发现，在有攻角情况下，尖锥边界层扰动功率谱峰值频率略有下降，且峰值对应的频带随攻角增大而变宽。

有攻角尖锥迎风面的激波强度比背风面更强，在边界层内产生一个压力梯度，黏性流与边界层外缘的无黏流存在剪切力，形成与外部势流流线相垂直的流动分量，即横流[9]。目前的实验和理论分析表明，在三维边界层中主要有3 种不稳定模态：低频的行进横流模态、高频Mack 模态以及定常横流涡高频二次失稳模态[10]，其中高频Mack 模态在大振幅定常横流涡的影响下会发生二次失稳。

在定常横流涡二次失稳研究中，通常会引入表面粗糙元诱发定常横流涡。Moyes[11]和Kocian[12]等分别对尖锥和椭圆锥的横流涡二次失稳进行了稳定性分析，发现二次失稳的z 模态位于涡的背部，y 模态则位于涡的顶部和底部。Li[13]和Choudhari[10]发现定常横流涡二次失稳模态的频率与无横流时Mack不稳定波的频率相当，且Mack 模态在定常横流涡二次失稳模态出现后快速增长。Craig[14]和Kocian[15]等利用热线风速仪进行了稳定性实验，发现定常横流涡和行进横流涡振幅沿轴向快速发展至饱和，并获得了定常横流涡的涡结构[14]，在涡背部有高频带能量集中，该高频扰动被认为是二次失稳。Ward 等[16-17]在静音风洞中利用表面压力传感器测得频率主要在40～50 kHz 的横流涡，以及在转捩为湍流之前出现的400 kHz 左右的高频压力脉动。根据该高频扰动对周向位置的依赖性，判断其为定常横流涡二次失稳引起的不稳定波。

Brog 等[18-19]在静音风洞和常规高超声速风洞中对HIFiRE-5 椭圆锥进行了实验。在静音风洞中，红外热像图显示模型表面出现了细横流条纹，在常规高超声速风洞中则未出现。压力脉动传感器在静音风洞和常规高超声速风洞中都获得了45 kHz 左右的功率谱峰值，与理论分析得到的行进横流涡频率相同。在常规高超声速风洞中，噪声会使第二模态扰动幅值增大，转捩前的高频扰动更可能是由第二模态导致[20-21]。目前，在噪声环境下对行进横流模态与高频模态之间相互作用的实验研究尚少。

为获得常规高超声速风洞中横流边界层内更多的高频扰动特征，本文采用高频压力脉动传感器（PCB）和聚焦激光差分干涉仪（Focused Laser Differential Interferometer,FLDI），在Mach 6 Ludwieg 管 风 洞中对6°攻角尖锥进行稳定性实验研究，获得了高频不稳定波幅值沿尖锥母线迅速增大后逐渐饱和的过程，以及高频不稳定波自相互作用沿尖锥母线的演变，发现了低频行进横流涡与高频不稳定波的非线性相互作用。实验还获得了不同来流雷诺数Re∞对高频不稳定波演变的影响，以及壁面法向和周向的密度脉动情况。

1 实验设备及测试技术

1.1 Mach 6 Ludwieg 管风洞

实验在华中科技大学航空航天学院的Mach 6 Ludwieg 管风洞中进行。该高超声速风洞由高压储气段、快速阀门、Laval 喷管、试验段和真空罐组成。试验段口径250 mm，其左右窗装有光学玻璃，以便进行光学实验。风洞采用电加热，本文实验来流总温为373 K。风洞自由来流归一化压力脉动为1.71%。

1.2 实验模型及PCB 安装位置

实验模型为长400 mm 的7°半锥角尖锥。为方便传感器安装，尖锥模型采用4 段式设计。模型安装于一个6°的攻角座上，并通过尾部支撑杆固定。沿尖锥模型母线安装7 个PCB，如图1所示。

图1 PCB 安装位置示意图Fig.1 PCB installation position

设定6°攻角时尖锥迎风线为0°方位角，背风线为180°方位角。通过旋转模型，调整模型与攻角座的相对位置，改变PCB 测试位置的方位角。在进行FLDI测量时，整体旋转模型和攻角座，并调整激光焦点位置，使焦点处于测试边界层内；同时利用电动位移台精确控制焦点在边界层厚度方向的位置，激光束刚好不被模型遮住时，设定测试高度为0 mm，以此为基准向上移动焦点。

1.3 聚焦激光差分干涉仪（FLDI）

FLDI 是一种基于光干涉原理的激光测试技术，具有较高的响应频率和空间分辨率，近年来被用于高超声速边界层第二模态不稳定波的测量[22-26]。如图2所示，被测试流场左右两边的光路分别为发射光路和接收光路。激光通过凹透镜C1 后成为扩散光束，通过偏振片P1 后，偏振方向完全一致，再被Wollaston 棱镜W1 按一很小的分离角分作偏振方向相互垂直、光强相等的两束光，而后被凸透镜C2 在流场测试位置聚焦为两个距离很小的焦点。焦点区A 即为光路测试区域。在焦点之后，光束经凸透镜C3 再次汇聚，并由Wollaston 棱镜W2 将两束分离光合并为一束，经偏振片P2 得到偏振方向完全一致的光束，最后由光电接收器D 将光信号转变为电信号。

图2 FLDI 光路图Fig.2 FLDI optical setup

由于光束的分离角很小，可认为两束激光在焦点区之前具有相同的光路，故相位差的影响可以忽略。在激光焦点区，两个焦点处气体密度不同导致折光率改变（式（1）），两束激光产生光程差并发生干涉，使得光电接收器上接收到的光强也发生改变。

式中，n为折光率，K为Gladston-Dale 常数，取2.257×10–4m3/kg，ρ为气体密度。

获得的电压信号与密度脉动之间的关系为[24]：

式中：Δρ为密度脉动量；ρL为当地密度；λ0为激光波长，实验中为632 nm；l为光路积分长度；U为光电接收器获得的电压幅值，UL为测试时间内的平均电压。

实验中，两个焦点的连线与来流速度方向平行，获得的值为密度脉动沿轴向的分量。

2 数据处理

实验中，为获得高频不稳定波，数据采集频率为3 MHz。风洞有效运行时间为100 ms，截取其中40 ms的信号进行分析，并进行11 kHz 的高通滤波。

功率谱密度是信号功率在频谱上的分布，定义为：

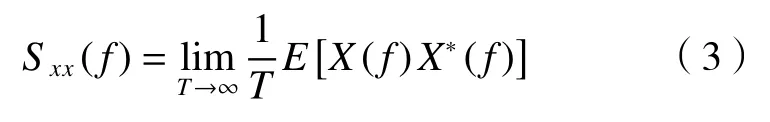
式中，X（f）表示数字信号时间序列的傅里叶变换，*表示共轭复数，T为信号长度，E[ ]表示期望值。对信号进行功率谱分析时，采用了50%重叠度的汉明窗。

另外，可以通过双谱分析获得边界层内各不稳定波之间的非线性相互作用。能量双谱定义为：

其反映了3 种频率不稳定波f1、f2和f3（f3=f1+f2）的非线性相互作用程度。与功率谱相比，Exxx（f1,f2）保留了相位信息，当波f1、f2和f3为二次相位耦合时，该值非零。

为在分析时去除不稳定波幅值对双谱值大小的影响，通常以式（5）将能量双谱值进行无量纲化。无量纲化后得到的双谱取值在[0,1]范围内，值越接近1，表示不稳定波之间的非线性相互作用越强，值为0 时，则意味着不存在非线性相互作用。

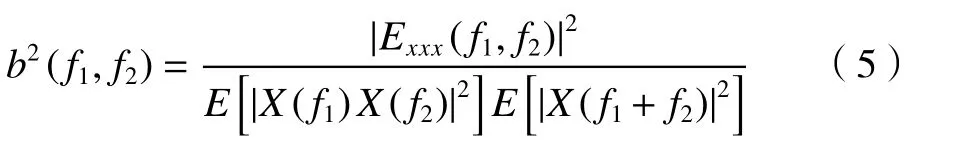
本文在进行双谱分析时，采用重叠度为50%的汉明窗，每个窗的采样点为1024 个，则频率分辨率为2929 Hz。

3 结果与分析

实验中，采用PCB 和FLDI 分别测试了尖锥边界层内的压力和密度脉动。由于位于尖锥357.02 mm处的PCB 在实验中损坏，故在测量90°方位角表面压力脉动时，缺失357.02 mm 处的PCB 数据。

3.1 120°方位角处不稳定波

来流雷诺数Re∞=1.0971×107m−1时，120°方位角母线上PCB 获得的压力脉动功率谱如图3所示。可以看出：在25 kHz 左右有低频峰值，在流向207.40 mm处开始出现高频不稳定波（200～400 kHz），该宽频信号的峰值频率在300 kHz 左右；功率谱幅值沿尖锥母线向下游逐渐增大，且频带也逐渐变宽，在287.79 mm处功率谱幅值达到最大；在287.79 mm 处下游，高频幅值降低，而低频部分的幅值明显增大；在337.42 mm处时，高频峰值消失，此时边界层逐渐转捩为湍流。

为获得不稳定波之间的非线性相互作用关系，对PCB 获得的压力脉动信号进行了双谱分析，结果如图4所示。在上游182.58 mm 处，高频不稳定波（230～375 kHz）呈现弱自相关，无量纲化后的相关系数在0.2 左右。同时，300 kHz 左右的高频不稳定波与低频不稳定波（20～40 kHz、65～85 kHz）存在弱非线性相互作用，使高频不稳定波频率范围变宽[27]。在207.40 mm 处，高频信号的自激励及高频与低频信号的非线性作用整体减弱，而280 kHz 的不稳定波自激励明显增强。在其后的下游，高频与低频信号（20～40 kHz）的非线性作用始终存在。Li 等[28]在相似工况下对尖锥进行了稳定性分析，结果表明行进横流比定常横流更不稳定，且不稳定频率范围为20～60 kHz。因此，实验获得的低频信号很可能为行进横流。在行进横流涡的作用下，高频不稳定波的频带范围展宽；同时，功率谱中对应的峰值频率的自激励逐渐增强，在257.02 mm 处达到最大。从图3可以看出，在下游337.42 mm 处，功率谱中的高频脉动幅值已经开始降低，双谱分析中的高频信号自相互作用减弱，且高频与低频行进横流的非线性相互作用完全消失，此时开始转捩为湍流。

图3 120°方位角处沿尖锥母线的压力脉动功率谱Fig.3 Power spectrum of pressure fluctuation along the generatrix at 120 ° azimuth

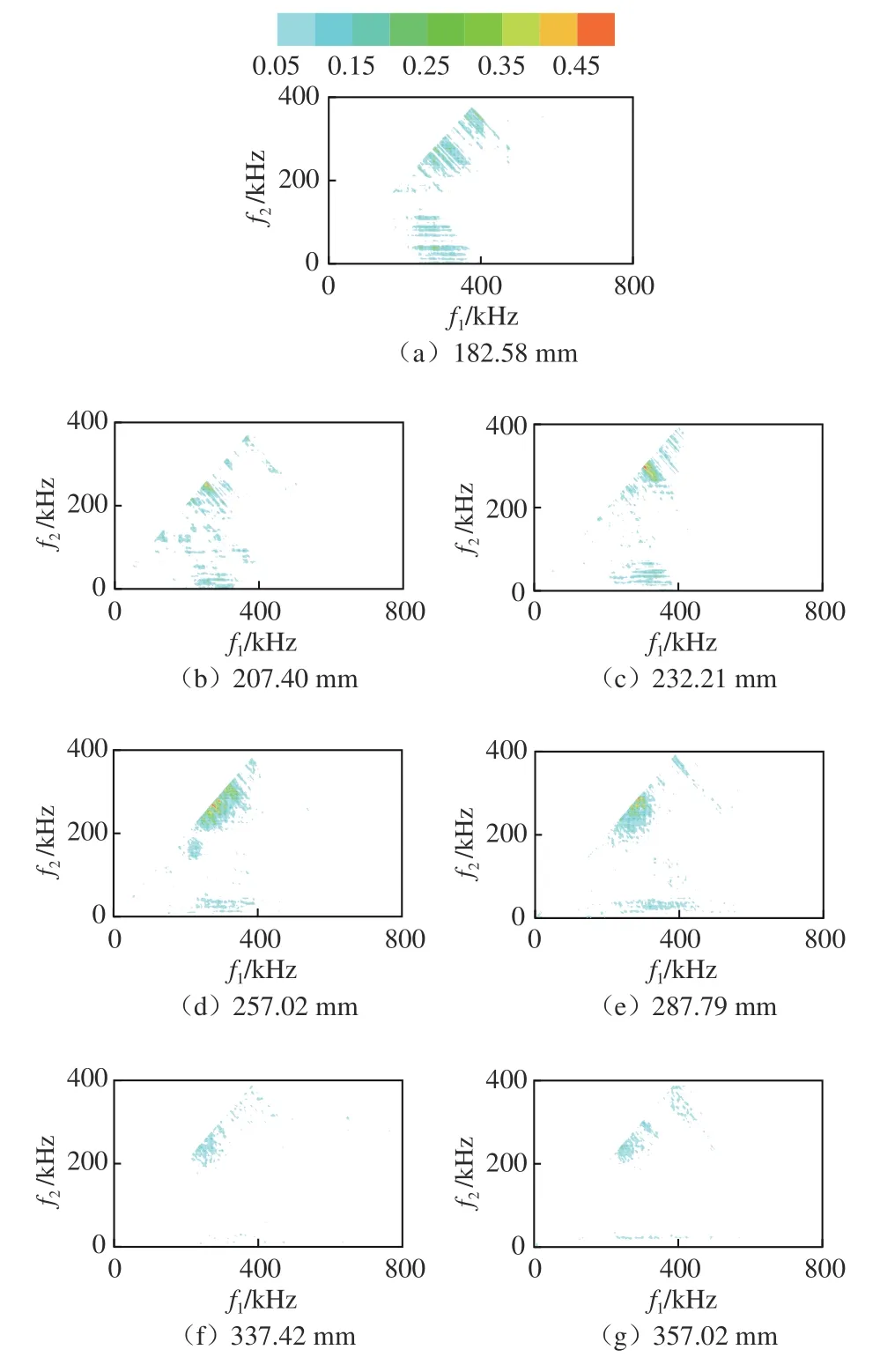
图4 120°方位角处的双谱分析结果Fig.4 Bispectral analysis results (120°)

3.2 90°方位角处不稳定波

旋转改变尖锥模型与6°攻角座的相对位置，获得Re∞=1.1790×107m−1时90°方位角母线上的压力脉动功率谱（图5）。低频部分的峰值在25 kHz 左右。在207.40 mm 之前，高频部分的幅值较低，边界层流动还处于稳定的层流状态。在232.21 mm 处出现一个250～420 kHz 的宽频信号，并在更高频率段有对应的二次谐波（500～840 kHz）。与120°方位角相比，90°方位角情况下的边界层厚度较薄，第二模态波对应的频率更高，获得的高频信号功率谱峰值频率也随方位角的增大而增大。在232.21 mm 处的下游，高频不稳定波快速发展，功率谱幅值和频率带宽都有所增大。在337.42 mm 处时，功率谱幅值不再继续增大，且低频信号对应的幅值变高，此时高频不稳定波达到饱和并将在下游破裂，发展为湍流。另外，在182.58 mm 处，功率谱中出现了一个160 kHz 的峰值，在向下游的发展过程中，该峰值一直出现（在207.40 mm处，未出现160 kHz 不稳定波信号，可能是此处的PCB 未捕捉到该不稳定波），这一不稳定波信号可能是高频与低频不稳定波相互作用产生的差频波。在207.40 mm 处的功率谱中，300 kHz 对应有一个峰值，其出现的原因目前尚不清楚。

图5 90°方位角处沿尖锥母线的压力脉动功率谱Fig.5 Power spectrum of pressure fluctuation along the generatrix at 90° azimuth

图6展示了90°方位角下的双谱分析结果。可以看出，在上游位置（182.58 mm），非线性作用比较弱，160 kHz 信号与200～600 kHz 的高频信号之间存在弱非线性作用。在207.40 mm 处，160 kHz 信号与高频信号的非线性作用依然存在；同时，400 kHz 左右的高频信号之间出现自激励及与低频信号的非线性相互作用。高频信号的自激励将产生二次谐波，但并未观察到高频信号与其二次谐波之间的非线性相互作用。在232.21 mm 处，高频信号与低频信号（20～60 kHz）的非线性作用明显增强，无量纲相关系数达到0.4，而高频信号的自激励减弱；同时还出现了160 kHz 与更高频信号的非线性相互作用，但这种相互作用较弱，无量纲相关系数不足0.1。从图5可以看出：257.02 mm 处的高频不稳定波幅值达到饱和，高频信号的非线性自相互作用达到最强；而400 kHz左右的高频信号与低频信号的相互作用减弱，在337.42 mm 处几乎消失。与120°方位角的情况相同，在高频不稳定波功率谱幅值增大阶段，高频不稳定波与低频信号之间存在非线性相互作用，但在90°方位角情况下该非线性相关作用更强。在高频不稳定波功率谱幅值饱和位置处，高频不稳定波与低频信号之间的非线性相互作用明显减弱。

图6 90°方位角处双谱分析结果Fig.6 Bispectral analysis results (90°)

3.3 不稳定波随雷诺数的变化

在3 个不同来流雷诺数（1.1382×107、1.0971×107和0.7542×107m−1）下，以PCB 测试了120°方位角尖锥母线上边界层内的压力脉动。

图7为不同来流雷诺数下257.02 mm 处的压力脉动功率谱图。可以看出：来流雷诺数Re∞较低时，高频不稳定波的功率谱幅值较低，对应的峰值频率较低；Re∞越高，低频部分的功率谱幅值越高。

图7 不同Re∞下的压力脉动功率谱Fig.7 Power spectrum of pressure fluctuation with different Reynolds numbers

将7 个PCB 测点的功率谱在对应带宽内进行积分，积分值的均方根可视为高频不稳定波的振幅。由于低频部分功率较大，故积分时可不予考虑，以免淹没高频信号。每个轴向位置高频不稳定波的频率范围不同，积分范围也有所不同。积分初始频率为高频峰值对应的功率谱开始增大处的频率，幅值达到峰值后，下降至其开始增大处所对应的频率为积分结束频率。图8为不同Re∞下120°方位角高频不稳定波振幅沿母线的变化。可以看出，Re∞=1.0971×107m−1时，振幅从第一个PCB 位置（182.58 mm）沿母线向下游呈现线性快速增大，在257.02 mm 处幅值增大趋势变缓。从双谱分析结果也可以看出，在257.02 mm 处宽频域的高频不稳定波之间的非线性相互作用最强，使不稳定波幅值增大趋势减缓。压力脉动幅值在287.79 mm 处达到最大值，之后在下游有所下降。当Re∞=0.7542×107m−1时，直到257.02 mm 处才出现高频不稳定波增长。与 高Re∞时（1.1382×107和1.0971×107m−1）的情况相同，压力脉动幅值先呈现线性增大，在337.42 mm 处达到饱和，随后幅值降低。总之，在不同Re∞下，高频不稳定波的初始振幅相当；Re∞越高，高频不稳定波幅值越早开始增大，且越早达到饱和幅值；同时，高Re∞下的高频不稳定波幅值的饱和值更大。

图8 不同Re∞下的压力脉动幅值沿母线的变化Fig.8 The amplitude of pressure fluctuation along generatrix with different Reynolds numbers

3.4 边界层内不同高度的不稳定波

Re∞=1.1790×107m−1时，以FLDI 在90°方位角下287.79 mm 处的壁面法向0.5、1.0、1.5 和2.0 mm 高度位置测量了密度脉动，功率谱如图9所示。可以看出，FLDI 在边界层内未测到160 kHz 的密度脉动。另外，在0.5 和2.0 mm 高度处密度脉动较小，而在1.5 mm 高度处高频密度脉动最为明显，且峰值对应的频率为200～400 kHz。与位于壁面处的PCB 信号相比，FLDI 获得的高频信号带宽存在约20 kHz 的偏移，可能是由FLDI 光路在三维边界层中的积分效应导致。实验时，为使激光焦点区位于测试的边界层内，将尖锥模型和6°攻角座一起旋转了90°。从图10可以看出，由于尖锥倾斜，光路穿过的并非同一轴向位置的边界层，且该边界层具有显著的三维效应，导致FLDI 与PCB 测得的不稳定波存在频率偏移以及不同边界层高度上的峰值频率偏移。同时，光路积分效应也可能是FLDI 未捕捉到160 kHz 峰值的原因。

图9 边界层内不同高度的密度脉动功率谱Fig.9 Power spectrum of density fluctuation at different heights in boundary layer

图10 激光经过6°攻角尖锥边界层示意图Fig.10 Optical path diagram

4 结 论

为研究常规高超声速风洞实验条件下三维边界层中的高频不稳定波特征，采用PCB 和FLDI 对6°攻角尖锥边界层内不稳定波的演化进行了初步的实验研究，得到以下结论：

1）常规风洞实验中，在90°和120°方位角下，6°攻角尖锥的边界层内都存在高频不稳定波。90°方位角下，高频不稳定波频率范围为250～420 kHz；120°方位角下，边界层更厚，不稳定波频率范围为200～400 kHz。

2）高频不稳定波幅值沿尖锥母线在上游呈线性快速增长，之后逐渐趋于饱和。在线性增长区，高频不稳定波与行进横流之间存在非线性相互作用，与120°方位角相比，在90°方位角下该相互作用更强。高频不稳定波与行进横流之间的非线性相互作用会使高频不稳定波的频谱展宽。当高频不稳定波的自激励作用达到最强时，其与行进横流之间的非线性相互作用明显减弱。

3）在高来流雷诺数下，高频不稳定波更早出现并增长至较大的饱和值。