非定常电场下锥射流的振荡行为研究

富庆飞，葛 斐，成锦博，杨立军，任军学，汤海滨

1.北京航空航天大学 宇航学院，北京 102206；2.西安航天动力研究所，西安 710100 3.北京航空航天大学 空间与环境学院，北京 102206

0 引 言

微小卫星要满足载荷任务要求，实现阻力补偿、精确姿态控制、轨道机动等任务目标，必须配备体积小、质量轻、比冲高、寿命长的推进系统。传统的化学推进系统很难满足这些要求，因此具有微小推力的电喷雾推进系统成为研究热点。电喷雾推进系统的主要原理是利用电场将导电液体雾化为带电液滴，并在电场作用下加速形成推力。在此过程中，液体的电雾化至关重要，直接决定了带电液滴的尺寸、产生效率和带电量，进而决定了电喷雾推进系统的推力、比冲等关键性能参数，因此，研究电雾化的产生机理与发展过程对电喷雾推进系统的设计具有重要意义。

定常电场下的电雾化产生机理与动力学特征研究均已非常完善[1-3]；而非定常电场具有很好的可调控性，结合空间发动机对电喷雾推进系统脉冲工作的实际需求，深入认识非定常电场作用下电雾化各种模式的产生机理与形态特征具有重要意义。

在非定常电场下，电雾化通常不会出现特别稳定的锥射流模式，电压变化导致的电场力扰动会使得流动状态无法一直保持稳定，射流通常呈现脉动状态。非定常电场下的电雾化研究多见于带电圆柱射流研究。Sato[4]采用施加非均匀交变电场的新方法产生了尺寸范围更大的均匀液滴。Sample 等[5]通过实验证实了交变电场的引入会提高射流产生液滴的均匀性以及产生液滴频率的可控性。Balachandran等[6]初步探究了交变电场对高导电液体静电雾化的影响，研究结果表明可以通过在静电场基础上叠加交变电场的方法控制液体射流。Huneiti 等[7]研究了静电场和交变电场耦合作用下高导电率液体射流的破裂行为，主要讨论了流量、振荡频率和电导率的影响。针对稳定锥射流在非定常电场扰动下振荡行为的研究，目前集中于定性实验研究方面。Deng 等[8]通过实验研究了受外部电场阶跃变化影响的泰勒锥的完整瞬态响应，分析了各种外部条件和物性参数对总响应时间的影响。Choi 等[9]通过从单个脉冲周期中导出电荷集聚时间、平衡法向电应力与表面张力，获得了振荡频率与施加电场参数的标度律。Paine等[10]对阶跃电压下锥射流尖端的电流脉冲进行了研究，结果表明瞬态射流的形成与发射电流中的振荡存在相同的频率。

在电喷雾推进系统内，脉冲工作是空间发动机的主要工作模式，此时雾化模式会极大地影响系统的推力和比冲。对非定常电场下的电雾化过程目前还缺乏系统性认识，有必要对其动力学特性进行深入研究。本文针对非定常电场作用下电雾化系统性研究缺乏的情况，结合空间发动机对电喷雾推进系统脉冲工作的实际需求，对非定常电场作用下锥射流的振荡行为进行实验研究，利用高速摄像机记录锥射流在非定常电压扰动作用下的脉动变形过程，探讨射流振荡频率与电压扰动频率的匹配关系。

1 实验设备与方法

1.1 实验设备

从金属喷嘴中流出的液体在电场力与表面张力的共同作用下膨胀为弯月面，在扰动电压作用下，弯月面发生破裂并形成射流。由于存在电场的持续扰动，射流形态发生周期性脉动，对这种振荡状态进行研究有助于理解非定常电场对射流模式的具体影响。本文搭建了电雾化实验系统，通过调整扰动电压、扰动频率以及喷嘴直径等参数，得到不同幅值与频率的正弦电压波形下的射流形态和振荡频率等，通过分析射流振荡频率与电压扰动频率的关系，研究射流形态和振荡与外加扰动的关系。

电雾化实验系统包括高压直流电源、信号发生器、高压放大器（4 kV，6 kHz）、静电计、示波器、高速摄像机、高功率光源、注射泵、胶管和不锈钢针头（即喷嘴）等。如图1所示。

图1 实验系统图Fig.1 Experimental system

整个实验系统可分为流量供给系统、电扰动及测量系统以及高速摄影系统等。

1）流量供给系统。采用注射泵（型号LSP01-1BH）向喷嘴提供稳定的流量。该注射泵最小体积流量为0.0901 μL/min，本实验所需液体流量较小（1～20 μL/min），此设备完全可以满足需要。

2）电扰动及测量系统。实验中施加的非定常电压由信号发生器与高压放大器共同产生，信号发生器输出较小的扰动电压，经高压放大器放大后施加到抽取极上（信号发生器型号为UTG2062A，高压放大器型号为609E，输入电压范围0～±4 V，放大倍数固定为1000，输入电压范围0～±4 kV，输出电流范围0～±20 mA，电压增益精度0.1%，转换速率>50 mV/μs，输入交流电压频率<6 kHz，失真率<1%）。实验中，采用在满足稳定锥射流条件的直流电压上叠加非定常扰动电压的形式施加非定常电压。经前期实验发现，满足稳定锥射流条件的电压在4 kV 以内，故所选高压放大器满足实验要求。

采用Keithley 公司的6514E 静电计（可测量电压范围±10 μV～±210 V，电流范围±100 aA～±21 mA，电阻范围10 mΩ～210 GΩ，荷电范围10 fC～21 μC）测量射流破裂后产生液滴的雾化电流值。配合RS232串口线与采集软件进行数据采集，在保证数据精度要求的前提下，实验中每秒可采集11 个数据点。

3）高速摄影系统。采用日本Photron 公司的FASTCAM SA-Z 高速摄像机，100 万像素（1024 像素×1024 像素）下帧率可达2×104帧/s，在低分辨率下最高帧率可达2.24×105帧/s，最小曝光时间0.25 μs，单个像素大小20 μm，具有开始、中心、随机、结束等多种触发模式。将常用微距镜头更换为物镜×1.5、目镜×10 的显微镜头，可进一步提高图像质量。另外，由于显微镜头进光量较小，实验中采用最大额定功率200 W 的灯源系统RF-200W 来改善光照条件，在满足画幅亮度的同时，尽可能缩短曝光时间，满足拍摄流动细节的需求。

使用无水乙醇作为实验工质，密度0.79 g/cm3，表面张力22.8 mN/m，黏度1.216 mPa·s。

1.2 实验方法

锥射流状态是电雾化中较为稳定的一种状态，目前对稳定锥射流的产生机理及发展过程都已有了清晰的认识，但关于非定常电压对稳定锥射流的扰动研究较少。在射流稳定的条件下施加电场扰动，锥射流的发展会呈现出明显的规律，因此实验中采用在满足稳定锥射流条件的直流电压上叠加非定常扰动电压的形式施加非定常电压，且施加的扰动电压波形均为正弦波。例如，设置非定常电压平均值为3.70 kV（施加直流电压为3.70 kV，此时电雾化处于稳定锥射流模式），正弦电压的最大值为3.90 kV，最小值为3.50 kV，即扰动幅值为200 V。实验中使用高速摄像机获得了不同扰动电压和扰动频率下的射流图像，如图2～5所示（帧率2×104帧/s，曝光时间0.25 μs）。

图2 100 V-100 Hz 的正弦波下射流图像Fig.2 Jet image under 100 V-100 Hz sine wave

图3 100 V-600 Hz 的正弦波下射流图像Fig.3 Jet image under 100 V-600 Hz sine wave

图4 200 V-800 Hz 的正弦波下射流图像Fig.4 Jet image under 200 V-800 Hz sine wave

图5 300 V-900 Hz 的正弦波下射流图像Fig.5 Jet image under 300 V-900 Hz sine wave

从图中可以看到，射流主要呈现出两种形态：保持锥射流形态的微小脉动，可称之为振荡锥射流模式（Oscillating Cone-Jet）；周期性喷射，可称之为间歇性喷射模式（Intermittent Jet），此模式下，射流在不同扰动幅值与扰动频率下的形态略有不同。进一步分析可以发现，在不同电压扰动幅值和频率下，射流呈周期性振荡。对射流进行二值化及轮廓提取，即可得到此时射流的振荡形态演化与振荡频率。图6为扰动幅值250 V、扰动频率900 Hz 时2 个周期内的射流轮廓，图7为扰动幅值100 V、扰动频率100 Hz 时2 个周期内的射流轮廓（T为振荡周期，n为帧数）。

图6 250 V-900 Hz 正弦波下的射流轮廓Fig.6 Jet profile curve under 250 V-900 Hz sine wave

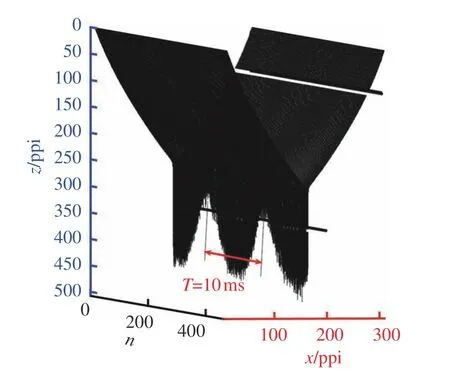
图7 100 V-100 Hz 正弦波下的射流轮廓Fig.7 Jet profile curve under 100 V-100 Hz sine wave

2 实验结果与分析

2.1 定常电场下的锥射流模式转变过程

本文在锥射流模式下施加非定常扰动电压作为扰动源，因此准确掌握稳定锥射流模式所需的电压与流量条件极为重要。当喷嘴规格为22 G、23 G 和24 G（外径分别为0.73、0.63 和0.55 mm，内径分别为0.41、0.33 和0.29 mm）时，模式相图的射流形态一致，因此在无量纲数中考虑喷嘴规格，得到喷嘴规格为22 G、23 G 和24 G 时电雾化模式转变BoE-Ca（电邦德数–毛细数）相图，如图8所示，图中坐标轴变量均进行了无量纲化。

图8 电雾化模式转变BoE-Ca 相图（喷嘴规格为22 G、23 G 和24 G）Fig.8 BoE-Ca phase diagram of electro-atomization mode transition when the nozzle diameter is 22 G,23 G and 24 G

电邦德数BoE反映了电应力与表面张力的关系。将喷嘴尖端的电场强度E定义为：

其中，U为电压，dO为喷嘴外径，L为喷嘴尖端到抽取极的距离。电邦德数[11]可定义为：

其中，ε0为气体介电常数，σ为表面张力。

毛细数Ca反映了黏度与表面张力的关系，定义为：

其中，v为流动速度，μ为动力黏度。

可以发现Ca=1.5×10－4为稳定锥射流模式与临界锥射流模式的分界点；BoE<0.5 时，射流呈现滴落模式；稳定锥射流模式出现在BoE=1.0 的邻域内，此时电场力与表面张力平衡，可形成稳定的泰勒锥；流量越大，射流进入双股射流模式所需的电场力越小。

图9为不同喷嘴规格下射流进入锥射流模式的开启电压。随着流量增大，开启电压增大，流量较大时，开启电压稳定在一定值，不再出现大的变化。此时射流通常处于临界锥射流模式，这种模式具有不稳定性质，射流发展具有不稳定模态，会与施加的非定常扰动电压造成的不稳定模态耦合，对最终结果产生影响。因此，在对非定常电场下的射流振荡规律进行研究时，实验中的流量参数通常选择较小的值（Q=5 μL/min）。

图9 不同喷嘴规格下电雾化进入锥射流模式的电压随流量的变化Fig.9 The change of the voltage of electro-atomization into cone jet mode with the flow rate under different nozzle diameters

2.2 非定常电场作用下锥射流的振荡频率研究

得到稳定锥射流所需的流量–电压条件后，在保证射流处于稳定锥射流模式（Cone-Jet）的条件下，在直流电压上叠加非定常扰动电压，射流会出现振荡锥射流和间歇性喷射两种模式。图10为电压扰动幅值Uamp=100 V 时射流振荡频率与电压扰动频率的关系曲线。可以发现，在不同的扰动频率下，曲线整体呈线性，在中间频率段（f=600～1200 Hz），射流振荡频率稳定在300～400 Hz 区间。

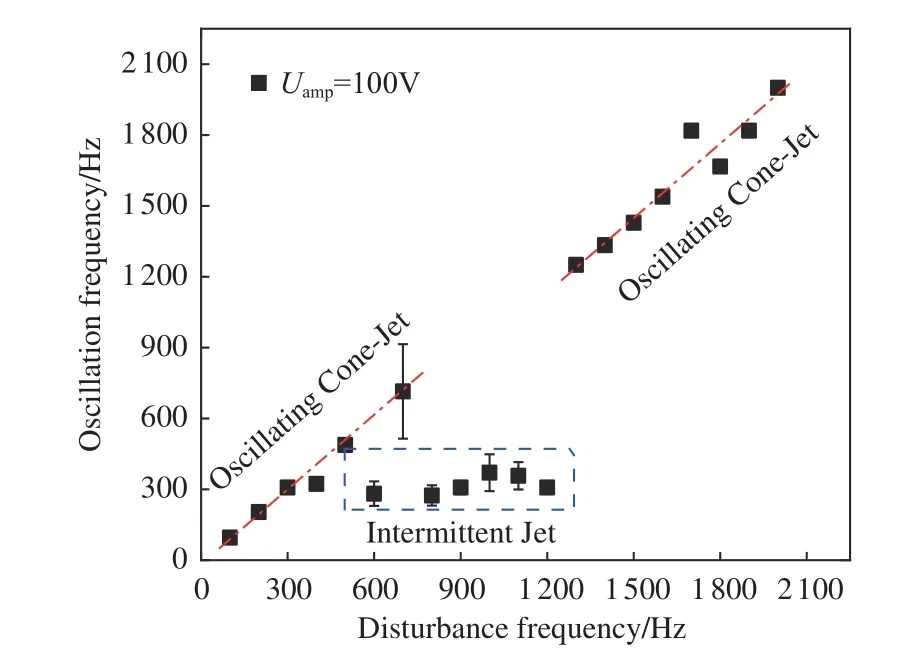
图10 扰动电压幅值为100 V 时射流振荡频率与扰动频率的关系Fig.10 The relationship between jet oscillation frequency and disturbance frequency when the disturbance voltage amplitude is 100 V

在射流发展过程中，毛细振荡频率由惯性力与表面张力的竞争作用决定，反映了射流对外界扰动的响应频率。瑞利频率（Rayleigh frequency）为[12]：

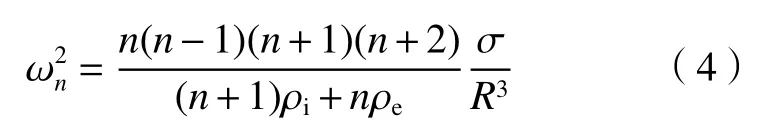
其中，ωn为瑞利频率，σ为表面张力，ρi和ρe分别为内外流体的密度，r为喷嘴外半径。在非定常电场下的射流振荡行为研究中，在实验条件下通过物性参数计算得到毛细振荡频率fc：

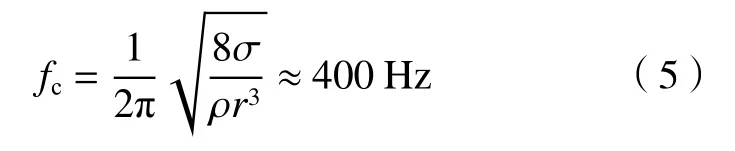
其中，ρ为工质（即无水乙醇）密度。可以发现，稳定段的射流振荡频率与毛细振荡频率相近，曲线呈现出两端斜率较大、中间段平缓的特征。

图11为电压扰动幅值Uamp=150 V 时射流振荡频率与电压扰动频率的关系曲线，依然整体呈线性，当电压扰动频率为700～800 Hz 时，射流进入间歇性喷射模式，其他频率均为振荡锥射流模式。图12～13 给出了电压扰动幅值为200 V 和250 V 时射流振荡频率与电压扰动频率的关系曲线，其振荡特征与电压扰动幅值为150 V 时相似。

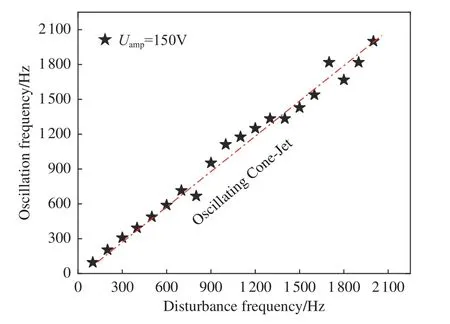
图11 扰动电压幅值为150 V 时射流振荡频率与扰动频率的关系Fig.11 The relationship between jet oscillation frequency and disturbance frequency when the disturbance voltage amplitude is 150 V

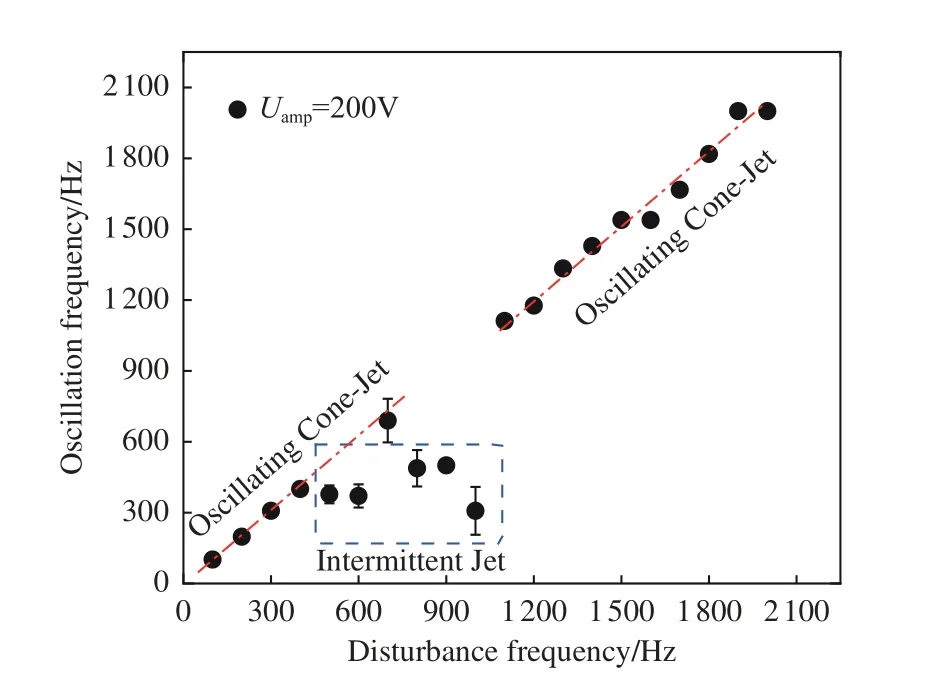
图12 扰动电压幅值为200 V 时射流振荡频率与扰动频率的关系Fig.12 The relationship between jet oscillation frequency and disturbance frequency when the disturbance voltage amplitude is 200 V

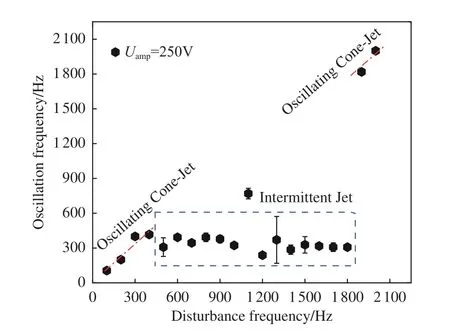
图13 扰动电压幅值为250 V 时射流振荡频率与扰动频率的关系Fig.13 The relationship between jet oscillation frequency and disturbance frequency when the disturbance voltage amplitude is 250 V

图14为Uamp=300 V 时射流振荡频率与扰动频率的关系曲线。由于电压扰动幅值过大，射流在f=100 Hz 时为振荡锥射流模式，其他频率下均为间歇性喷射模式，射流振荡频率在300～500 Hz之间。

图14 扰动电压幅值为300 V 时射流振荡频率与扰动频率的关系Fig.14 The relationship between jet oscillation frequency and disturbance frequency when the disturbance voltage amplitude is 300 V

在低频段，受电压变化与流量供给的影响，一个电压周期内产生一次振荡，因此射流振荡频率与电压扰动频率接近；当频率增大，锥射流受到的扰动增大，原本稳定的锥射流无法继续保持稳定，此时射流以固有振荡频率（毛细振荡频率）脉动；频率继续增大，由于电驰豫时间与毛细时间的尺度差异较大，在较大频率下锥射流形态不足以在一个电压周期内发生变化，只能以锥射流形态继续脉动，此时射流振荡频率与电压扰动频率相近。

2.3 非定常电场下电雾化过程的流动模式分析

在振荡锥射流模式下，射流在电场扰动下会保持锥射流形态，并在锥尖产生喷射，多发生于扰动幅值较小时；在间歇性喷射模式下，由于施加的扰动幅值较大，锥射流无法保持原来的形态不变，在发生射流喷射后会向喷嘴方向反弹。图15为电压扰动幅值100 V、扰动频率1200 Hz 时的典型射流形态变化。在发生喷射的瞬间，射流的弯月面由锥形过渡为圆弧形，喷射流体在脱离弯月面初期呈细长梭形。越靠近喷嘴，流体所受电场力越大，电场加速作用越强，因此越靠近喷嘴的流体速度越快；另外，梭形流体在空气扰动下分段破裂为小液滴，并最终自上而下合并为大液滴。

图15 100 V-1 200 Hz 时射流形态Fig.15 Jet form at 100 V-1 200 Hz

根据射流喷射图像并结合实验条件，可估算出电压扰动幅值200 V、扰动频率900 Hz 时喷射出的梭形流体的平均速度为3.60 m/s；而电压扰动幅值100 V、扰动频率1200 Hz 时喷射出的梭形流体的平均速度为5.04 m/s。由此可见，扰动频率越大，梭形流体的平均速度就越快。图16为扰动幅值Uamp=250 V 时梭形流体平均速度随电压扰动频率变化的曲线。随着扰动频率增大，梭形流体平均速度不断增大。

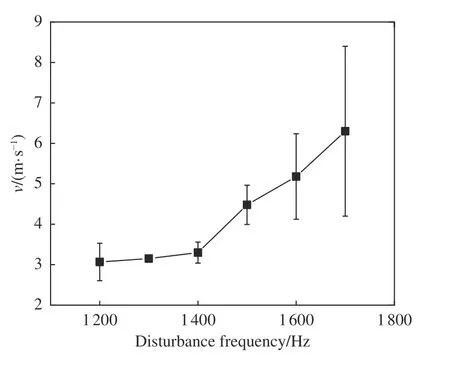
图16 扰动幅值为250 V 时梭形流体速度与扰动频率的关系Fig.16 The relationship between the speed of the shuttle fluid and the frequency of the disturbance when the disturbance amplitude is 250 V

当施加低幅值低频率的非定常电压时，射流会保持为锥形形态。图17为电压扰动幅值200 V、扰动频率400 Hz 时的典型射流形态变化。此时射流整体呈锥状，其尖端喷出细小射流，以摆动液丝形式向下游发展，并在空气扰动作用下分段破裂为微小液滴。

图17 200 V-400 Hz 时射流形态Fig.17 Jet form at 200 V-400 Hz

在振荡锥射流模式下，射流通常保持锥形，且在尖端发生微小喷射。在此过程中，微小振动会引起锥形的微小变化，反映在射流形态上，最明显的就是射流锥角的变化。如图18所示，射流锥角即泰勒锥的全锥角，提取泰勒锥区域的边界轮廓并以直线拟合，两直线相交于一点，其夹角即为本文所定义的射流锥角。图19为电压扰动幅值100 V、扰动频率100 Hz时的射流锥角测量值曲线。可以看出：锥角随时间变化呈现微小振荡，平均值Asa=62°；在微小振荡之外，锥角还呈现出规律性振荡，振荡频率在5 Hz 左右，说明非定常电场下的射流振荡行为是不同振荡模态共同作用的结果，体现在频率域中，射流具有不同的振荡频率峰值，但射流形态中体现出的频率主要为低阶模态，也最容易表现出来。

图18 射流锥角定义Fig.18 Definition of cone jet angle

图19 100 V-100 Hz 射流锥角测量值曲线Fig.19 100 V-100 Hz cone jet angle measurement curve

图20为电压扰动幅值100 V、扰动频率300 Hz时的射流锥角测量值曲线。射流锥角平均值为69°，微小振荡之外射流锥角的振荡频率在1 Hz 左右。

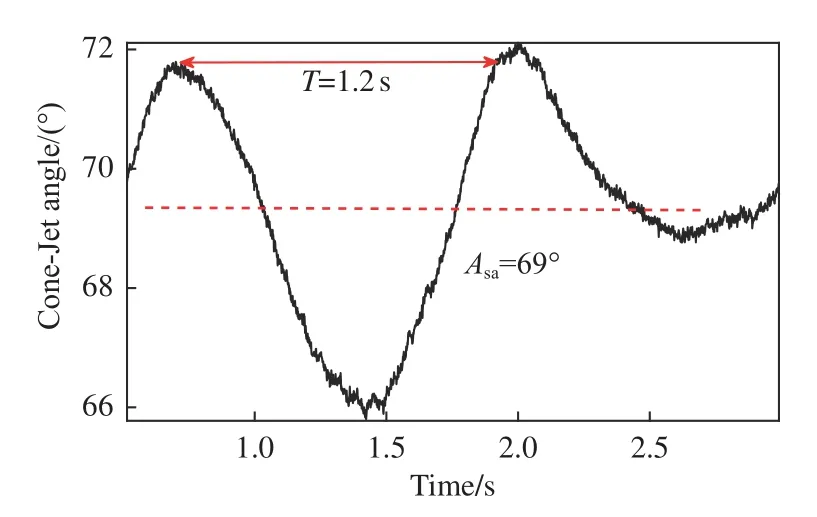
图20 100 V-300 Hz 射流锥角测量值曲线Fig.20 100 V-300 Hz cone jet angle measurement curve

图21为电压扰动幅值100 V、扰动频率700 Hz时的射流锥角测量值曲线，射流锥角平均值为77°，振荡频率在1 Hz 左右。

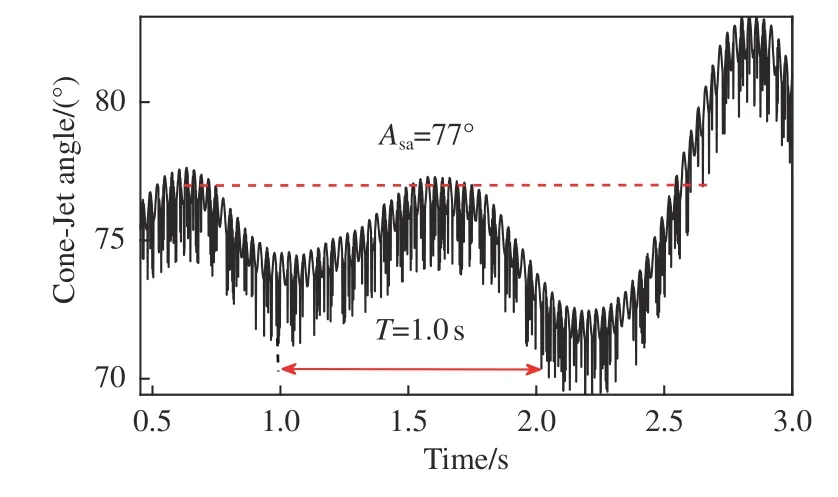
图21 100 V-700 Hz 射流锥角测量曲线Fig.21 100 V-700 Hz cone jet angle measurement curve

图22为电压扰动幅值100 V、扰动频率1500 Hz时的射流锥角测量值变化曲线，射流锥角平均值为83°，振荡频率在1 Hz 左右。

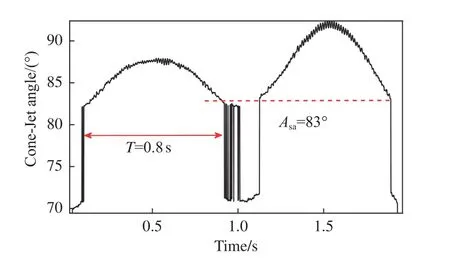
图22 100 V-1 500 Hz 射流锥角测量曲线Fig.22 100 V-1 500 Hz cone jet angle measurement curve

综上所述，电压扰动频率越高，射流锥角越大；在与射流形态相关的振荡模态之外，还存在其他振荡频率的非定常扰动作用于锥射流，该振荡频率随着非定常电压扰动频率的增大而增大，并在较大频率下接近定值。

对射流振荡频率与施加电压扰动频率的关系进行分析时指出，在非定常电场下射流表现出两种振荡模式，分别是振荡锥射流模式与间歇性喷射模式。进一步研究发现，液体流量的不同也会影响振荡模式所处的频率区间。图23为扰动幅值为100 V 时不同扰动频率与液体流量下的振荡模式分布区域相图。间歇性喷射模式出现于中间频率处，占整个实验频率区域较小；当体积流量为5 和7 μL/min 时，在整个100～2000 Hz 频率区间内，未出现间歇性喷射模式，射流均以振荡锥射流模式存在。

图23 扰动幅值为100 V 时振荡模式的分布相图Fig.23 The distribution phase diagram of the pulsation mode when the disturbance amplitude is 100 V

图24为扰动幅值为200 V 时不同扰动频率与液体流量下的射流振荡模式分布区域相图。在不同体积流量下，间歇性喷射模式均出现于中间频率区域；与扰动幅值为100 V 时的相图相比，间歇性喷射模式区域进一步扩大。

图24 扰动幅值为200 V 时振荡模式的分布相图Fig.24 The distribution phase diagram of the pulsation mode when thedisturbance amplitude is 200 V

图25为扰动幅值为300V 时不同扰动频率与液体流量下的射流振荡模式分布区域相图。此时，在所有流率与频率下，射流均为间歇性喷射模式，说明扰动幅值过大，使得射流无法保持原来的锥形形态。

图25 扰动幅值为300 V 时振荡模式的分布相图Fig.25 The distribution phase diagram of the pulsation mode when the disturbance amplitude is 300 V

图26为不同体积流量下稳定锥射流模式的开启电压。在不同流量下，形成稳定锥射流所需的直流电压条件不同，射流所受的绝对电场强度随着流量增大而增大，因此，在相同的扰动幅值下，间歇性喷射模式所处的频率区间在不同流量下存在一定差异。

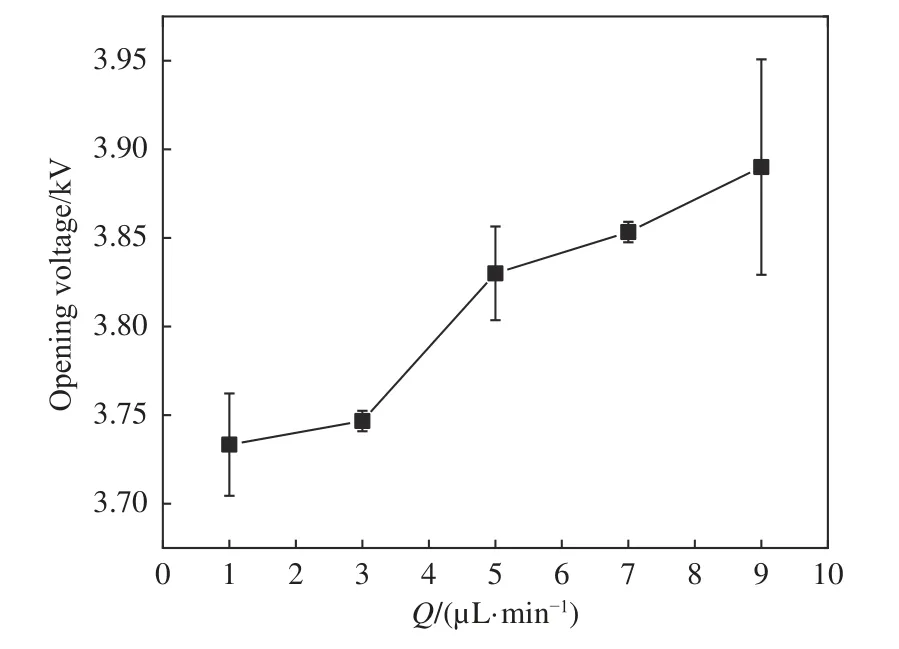
图26 不同体积流量下稳定锥射流的开启电压Fig.26 The opening voltage of a stable cone jet at different volume flows

3 结 论

通过搭建的非定常电场作用下的电雾化实验系统，得到了非定常电场作用下的射流形态图像和射流振荡频率等，通过分析射流振荡频率与施加电压扰动频率的关系，研究了射流形态及振荡与外加扰动的关系，得到如下结论：

1）在非定常电场作用下，射流振荡频率随电压扰动频率增大而增大。扰动频率较小时，射流振荡频率与电压扰动频率接近，且此时射流处于振荡锥射流模式；扰动频率处于中频范围时，射流振荡频率处于300～500Hz 范围内，此时射流处于间歇性喷射模式；扰动频率处于高频范围时，射流振荡频率与电压扰动频率接近，且此时射流处于振荡锥射流模式。

2）非定常电压扰动幅值越大，射流处于间歇性喷射模式的频率范围越大，处于振荡锥射流模式的范围越小；电压扰动频率越高，处于振荡锥射流模式的射流锥角越大。