多线性积分算子广义交换子在广义加权Morrey空间中的有界性

俞智慧,张慧慧

(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)

1 引言及主要结论

分数次积分算子在调和分析领域扮演着重要的角色,此类算子在微分方程,Sobolev嵌入定理等方面有着重要的应用。1999年,Kenig和Stein[1]研究了一类多线性分数次积分算子并且得到了这类算子在乘积Lp空间中的有界性。

与此同时,积分算子的加权理论也引起了数学工作者的极大重视。上世纪70年代,Muckenhoupt和Wheeden[2－3]分别引入了Ap和A(p,q)权函数类并且证明了奇异积分与分数次积分的加权模不等式。

Chen和Xue[4]中引入了一类多线性矢量权函数类AP→,q权函数类并且证明了多线性分数次积分算子的加权模不等式。接下来给出AP→,q权函数类的定义。

定义1.1[4]令其中wi均为Rn中的非负可积函数。如果下列条件成立:

积分算子交换子作为调和分析领域的一类重要算子,其在偏微分方程领域有重要的应用。读者可以参

见[5]等文献。2001年,Ding[6]研究了如下一类分数次积分算子广义交换子并且Ω为一个零次齐次函数。这里Rm(A;x,y)的定义为:

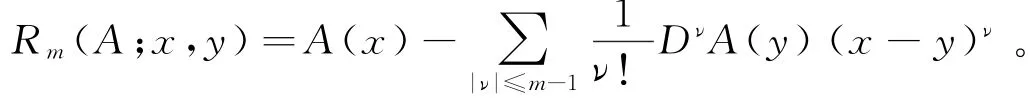
显然当m＝1时,算子即为Chanillo于1982年在文献[5]中研究的分数次积分算子交换子,因此可以看成是经典分数次积分算子交换子的推广。

1938年,Morrey[7]引入了如下一类以其名字命名的Morrey空间Mp,λ(Rn)(0≤λ＜n,1≤p＜∞):

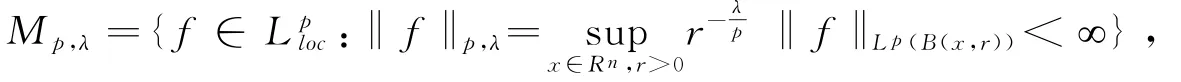
Morrey空间引起了数学工作者的极大兴趣并且也对此类空间做了推广。Guliyev[8]研究了如下一类广义加权Morrey空间:

定义1.2[8]假设φ(x,r)为Rn×(0,∞)上的一个非负可测函数。如果一个非负局部Lp(p≥1)可积函数f满足:

则称f属于广义加权Morrey空间

受到上述文献的启发,本文将研究如下一类具有粗糙核的多线性算子广义交换子,其定义为:

其中0＜α＜mn,Ni≥2,Ωi∈Ls(Sn－1)(s＞1)。

本文主要结果如下:

引理1.2 显然,定理1.1推广了文献[8－10]中的主要结论。

2 主要引理

引理2.1[11]假设b的m阶导数属于空间,则有:

3 主要的证明

故可得:

接下来估计Ii。利用Holder不等式,可得:

所以有:

于是有:

接下来估计IIij,可将IIij分解为:

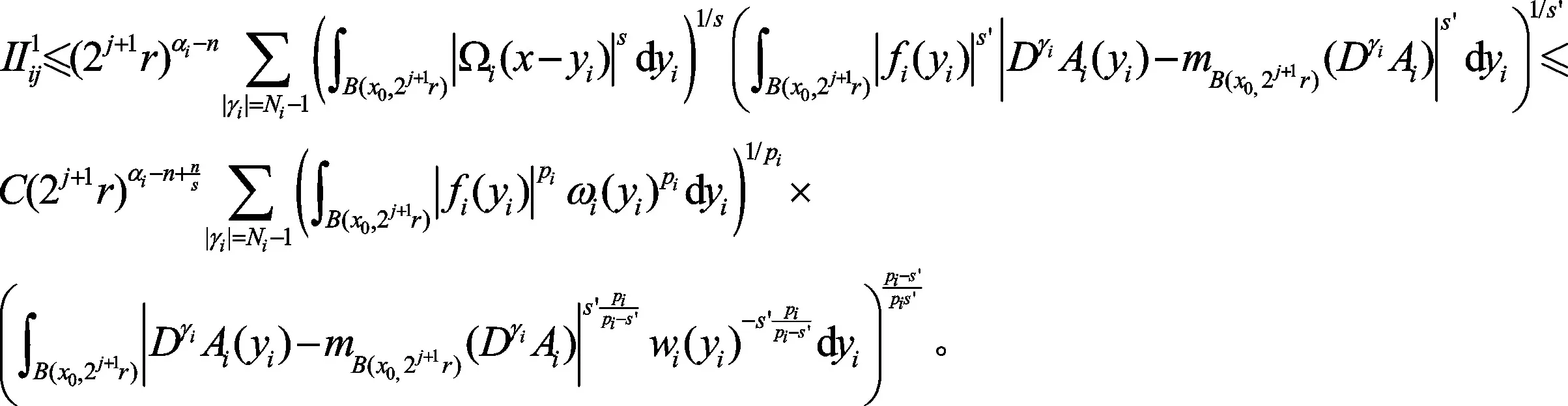
令:

分解其为:

接下来利用文献[9]中的相关估计,可得:

综合A1和A2的估计,有:

根据上述估计以及类似于Ii的估计过程,可得:

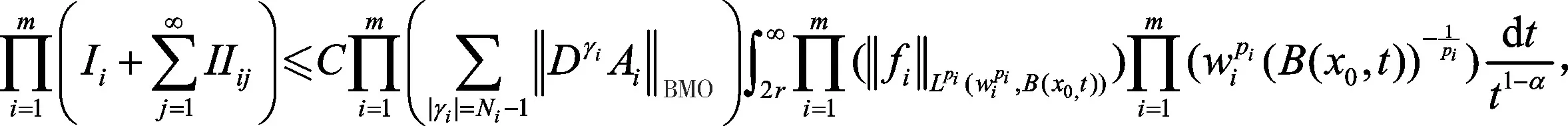
再次使用引理2.3,有:

分析II的估计过程,易得:

再次利用(3),有:

即:

根据(4)～(6),有:

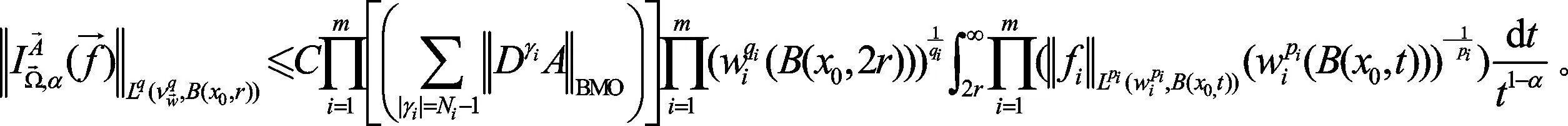
最后,根据引理2.3,可得:

根据条件(1),以及文献[10]中的相关证明方法与估计,可以通过(7)得到(2),故定理1得证。