高频高精快刀伺服系统优化

2022-01-20张建国李江黄凯郑正鼎杨辉许剑锋

光学精密工程 2022年1期

张建国，李江，黄凯，郑正鼎，杨辉，许剑锋*

高频高精快刀伺服系统优化

张建国1，李江1，黄凯1，郑正鼎1，杨辉2，许剑锋1*

（1.华中科技大学机械科学与工程学院，湖北武汉 430074；2.北京航空精密机械研究所，北京 100076）

研制了一款高频响、高精度及大驱动力的压电驱动型快速刀具伺服（Fast Tool Servo，FTS）装置，采用广义圆锥线拟合的柔性铰链构造新颖的柔性机构，通过对称布置的结构消除柔性刀架工作过程中在非期望运动方向的耦合误差，并对机构的运动学特性进行了综合建模。综合考虑装置行程和固有频率的设计目标，基于改进的BP神经网络优化算法，对柔性机构的结构尺寸进行了多目标优化设计。使用优化后的结构参数建立FTS装置的三维模型并通过ANSYS软件进行有限元分析，分析结果表明，优化后的柔性机构可以达到预期性能要求，验证了该优化算法的可行性。最后，进行了实验样机的制造和性能测试，进一步验证了FTS装置的优化设计结果。测试结果表明：FTS装置的固有频率超过7.6 kHz，标称行程约为6.4 μm，分辨率约为12 nm，跟随精度约为0.3 μm，静态和动态性能均符合设计目标。

超精密加工；快速刀具伺服装置；柔性刀架；优化设计；有限元分析

1 前　言

快速刀具伺服（Fast Tool Servo， FTS）切削在微纳米结构功能性表面制备等领域是一项极具发展前途的超精密加工技术。FTS最早出现于20世纪80年代，劳伦斯利弗莫尔国家实验室（LLNL）帕特森等设计了一种用于误差补偿的微进给系统［1］，随后麻省理工学院、GIT、东北大学、Precitech、摩尔纳米技术公司等对FTS进行了大量研究，该技术得以快速发展［2］。国内对FTS的研究起步较晚，但是近年来国内学者在该领域加大了研究力度，目前已取得显著的研究成果［3-6］。

微/纳米功能性表面结构可以通过超声共振和非共振振动的切削方式进行加工。超声共振的切削效率高，但共振轨迹难以控制［7］。FTS属于典型的非共振振动切削类型，在加工复杂微/纳米结构的光学元件时表现出更高的灵活性。一个完整的FTS系统主要由驱动系统、运动传导系统、末端执行器和控制系统4部分组成［8］。在近几十年，大量学者致力于FTS的研究，通过设计不同类型的FTS期望获得更优良的性能。

FTS装置的关键性能指标主要包括行程、刚度和跟踪精度等，各参数之间相互影响。行程决定了FTS装置能够加工的面形范围和补偿的误差幅值范围，刚度、精度和分辨率直接影响柔性刀架对各种信号的实时跟踪能力。动力源和运动传导机构的性能对FTS的工作稳定性也有很大影响。柔性机构具有结构简单，可储存弹性势能，运动精度高等特点，在微机电系统、精密定位、无装配设计和仿生机械等领域中得到了广泛的应用。根据结构分布，柔性机构可以大致分为并联式和串联式两种。相比于串联式柔性机构，并联式柔性机构非运动方向的耦合误差小，无间隙，摩擦可以忽略，其优点更加突出［9］，更适合作为FTS的柔性刀架［10-11］。对于动力源，压电陶瓷促动器（Piezoelectric Ceramic Actuator， PEA）可通过压电效应将电能转化为机械能输出，具有体积小、响应频率高、运动精度高等优点［11］。因此，本文选择并联式柔性机构和封装PEA分别作为FTS装置的运动传导机构和动力源。行程和工作频率是FTS两个最重要的指标。然而，这两个指标是互相矛盾的，过大的行程和频率会导致压电陶瓷致动器发热严重无法正常工作，而增大行程必然会降低工作频率［12］。因此，在设计FTS时需要综合考虑行程和频率，在满足行程需求的基础上频率应尽可能大［11］。同时，FTS的行程和频率极大程度上取决于柔性刀架的性能，而后者又依赖于柔性机构的结构参数［13］，这就涉及机构的多目标优化问题。一种最常用的方法是基于大量的有限元仿真，最终选择出最接近设计目标的方案［11，14］。此外，还可以通过数学建模，建立柔性机构精确的数学计算模型，求解各个设计目标，然后通过构造评价函数，将多目标优化问题转化为评价函数的单目标优化问题，求解得到的最优解即为最终解，从而获得满足特定性能的结构参数［10，12，15］。但是，这种方法需要建立准确的行程、频率等待优化目标的计算模型，且各种模型都有自身的限制，无法应用于所有的机构，如果柔性机构的结构较为复杂，建模过程也会变得极其复杂。这样的优化方法需要设定一个目标值，再无限逼近于目标值，很难得到真正的全局最优解［16-17］。基于上述考虑，本文结合两种优化方法，对柔性机构的多目标优化方法进行探索，使用改进的BP神经网络算法进行FTS柔性机构的多目标优化设计。通过研究柔性机构的结构参数和性能指标之间的映射关系，借助ANSYS仿真结果训练关系模型，设定目标值即可一次求解出对应的结构参数，有效简化了优化设计过程。

综上，FTS加工技术具有振幅和频率可控、能快速改变切削深度的特点。因此，本文进一步对快刀伺服加工技术展开研究，对高频高精FTS的结构设计、运动学和动力学建模、性能优化等进行研究，开发了一款高频高精快速刀具伺服装置，该装置拥有良好的典型微结构加工能力，对提高光学元件的加工效率，改善光学元件的使役性能等具有重要意义。

2 FTS结构设计

柔性刀架作为FTS的核心部件，起到支撑、运动传导等作用，直接决定装置的行程和动态响应频率。因此，设计结构简单和紧凑合理的柔性刀架尤为重要。柔性铰链作为柔性刀架的核心结构，常见的柔性铰链可以分为直圆、直梁、直梁-圆弧形和椭圆形4种。直圆形铰链将旋转中心视为圆心，运动精度极高，运动范围小。直梁形铰链转动范围大但运动精度低，直梁-圆弧形铰链是将两者结合起来形成的新型铰链，为了兼顾运动精度和范围，学者又提出了椭圆形柔性铰链，但设计较复杂，其特性参数亟需进一步研究。本文采用广义圆锥曲线描述柔性铰链的缺口轮廓，理论上，通过选择合适的参数就可以得到任意一种形状的圆锥曲线型柔性铰链，对铰链的缺口形状和尺寸参数进行优化，便可得到满足目标设计要求的柔性铰链。

广义圆锥曲线型缺口轮廓铰链的结构如图1所示。假设铰链的切口长度为2，切口深度为，宽度和最小厚度分别为和，为焦点，为准线，（>0）为焦点到准线的距离，为离心率。利用参数方程，缺口轮廓用数学方法表示为：

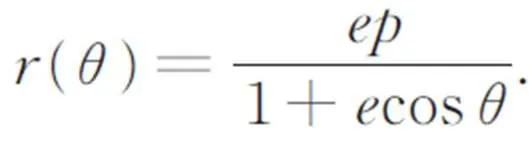
当01时，缺口轮廓形状为双曲线。当e0时，轮廓形状趋向于圆，，lim为直圆形缺口轮廓的切割半径。

为了搭建所述的FTS装置，双平行四边形结构被设计用于FTS装置的支撑和运动传导结构。与由一根刚性梁和两个铰链构成的传统连杆机构不同，本文采用式（1）所描述的圆锥曲线形柔性铰链，将一对共轴连接的两个柔性铰链重新排列，使它平行于另一对铰链以获得更大的轴向刚度，从而设计尽量简洁。最终设计的FTS三维模型如图2（a）所示，装置剖面图如图2（b）所示。为了保证实际工作中PEA与柔性刀架始终能够保持良好的接触从而使得驱动力较好地传递，PEA输出端设计为直径为1.5 mm的球形，并使用预紧螺栓对PEA施加预紧力。传感器支座和位移测量板借助螺栓与柔性刀架相连，用于微/纳米切削的金刚石刀具借助螺钉固定于柔性刀架上。

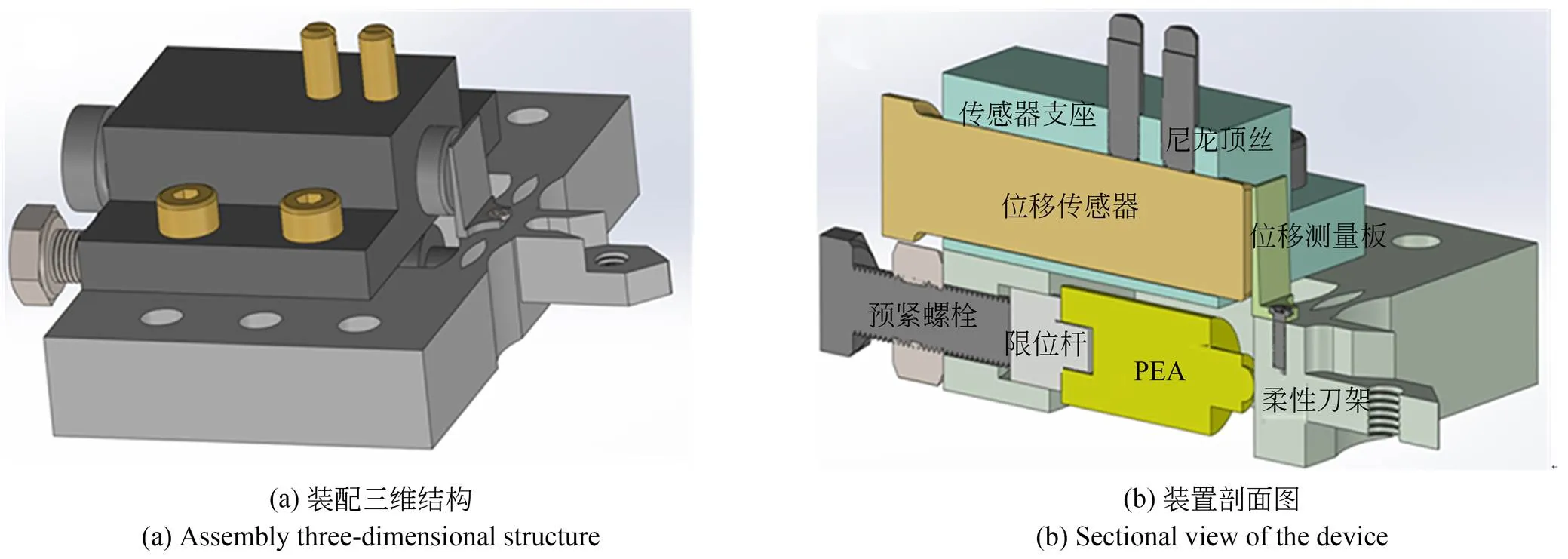
图2　快速刀具伺服机械结构示意图

3 FTS关键部件运动学分析

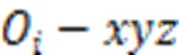
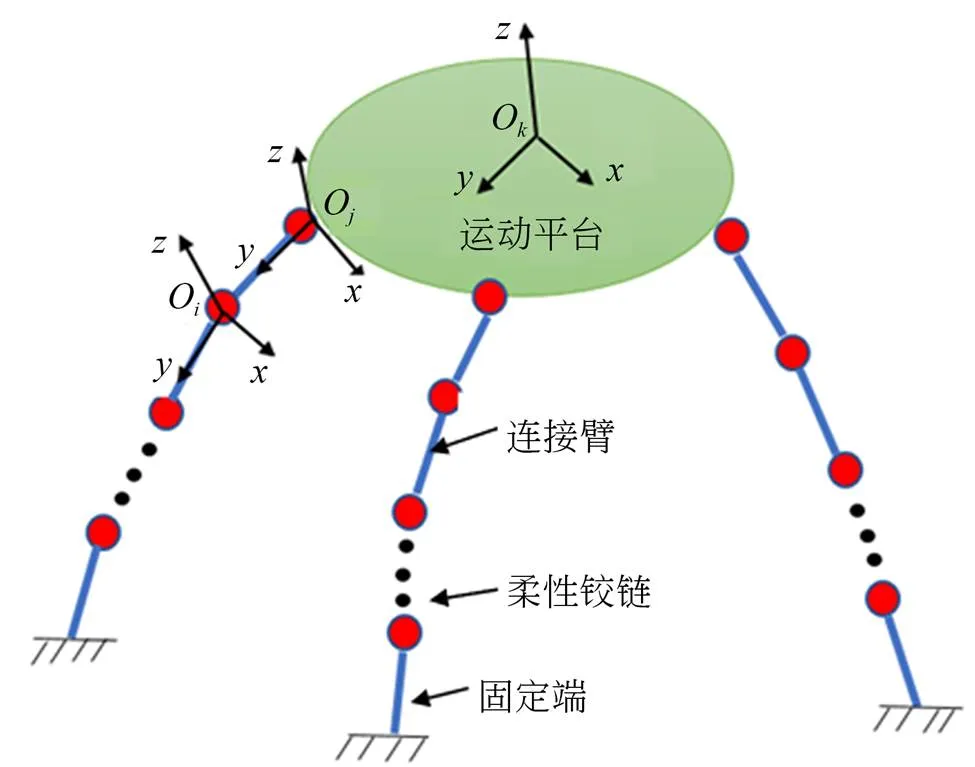
图3　典型柔性机构原理简图［19］

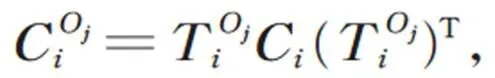
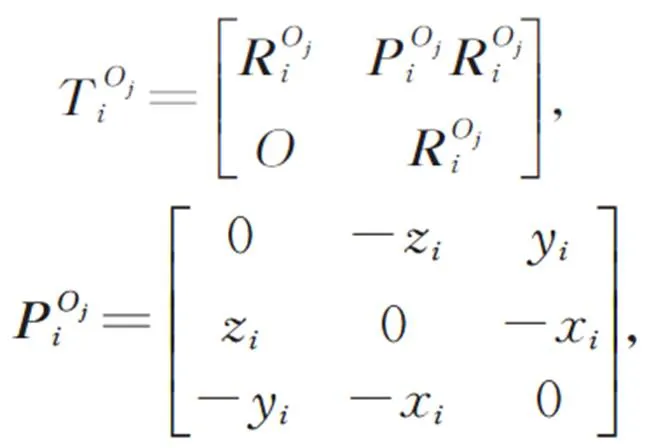
因此，任意一条由个柔性铰链串联而成的柔性链的末端相对于固定端的总柔度矩阵为：

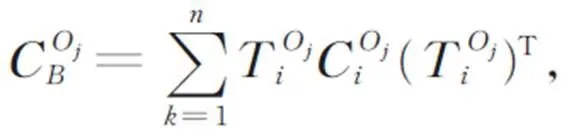
由个柔性链并联支撑的移动平台输出端的总柔度矩阵为：

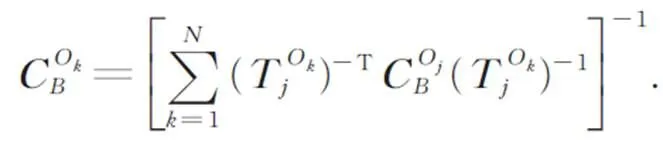
理论上，通过认定柔性机构的串并联特征就可以使用以上公式建立任意特征柔性机构的全柔度模型。

柔性刀架的关键部位由圆锥曲线形柔性铰链组成，柔性刀架的整体结构如图4所示，结构关于中线对称。柔性铰链之间的连接臂的变形相对于柔性铰链的变形很小，可以忽略不计，在后续建模中将中间连接臂视为刚体，可以简化柔性机构的建模仿真过程。

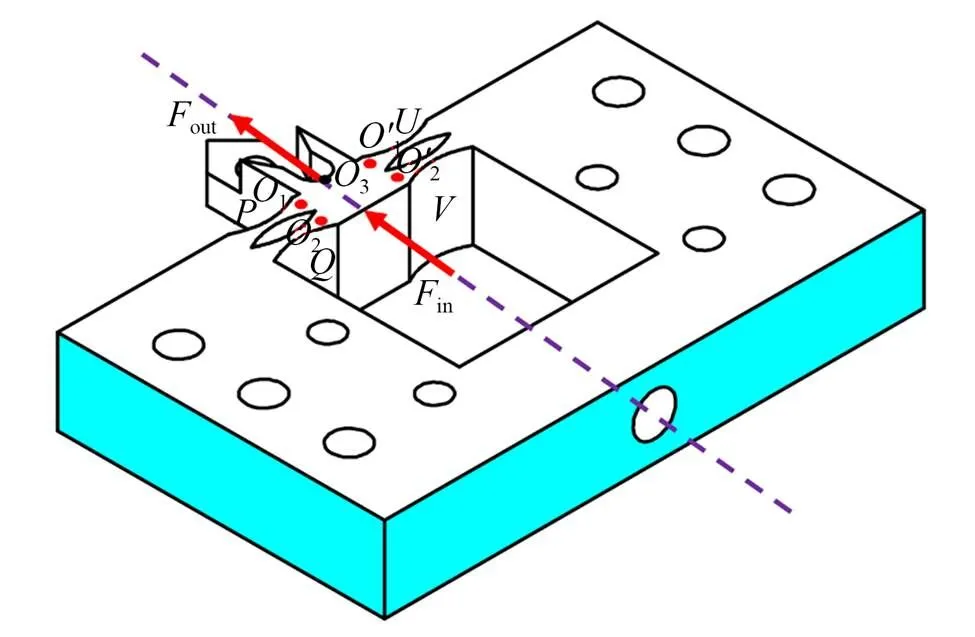
图4　柔性刀架示意图

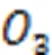
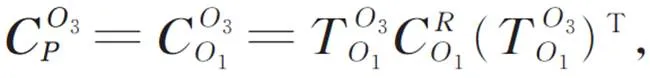
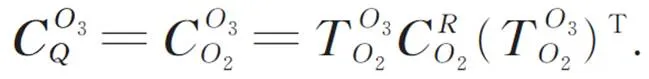
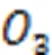
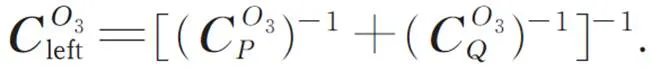
由于柔性机构结构对称，所以柔性机构的整体柔度为：

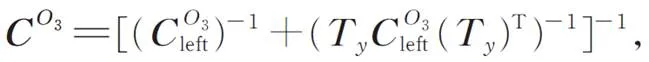
根据PEA的自身特性，只要PEA外部连接的机械结构存在刚度，则实际输出位移就一定会有损失，即位移损失现象。这一特性使柔性机构的实际行程小于PEA的标称行程。柔性机构的实际行程与PEA的标称位移之间遵循如下关系：

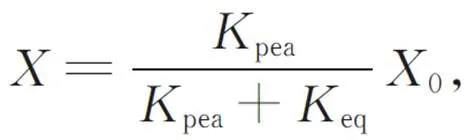
式中：pea为PEA的刚度，0为PEA的标称行程，eq为柔性机构整体的等效刚度。由机械振动学知识可知，柔性刀架的1/2结构的势能为：

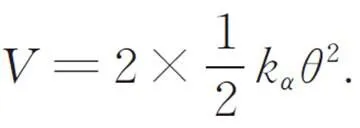
柔性刀架的1/2结构的动能为：

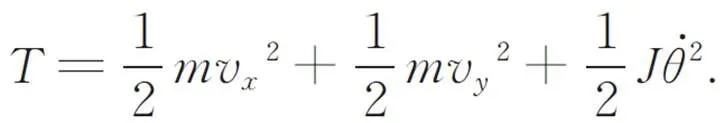
假设：

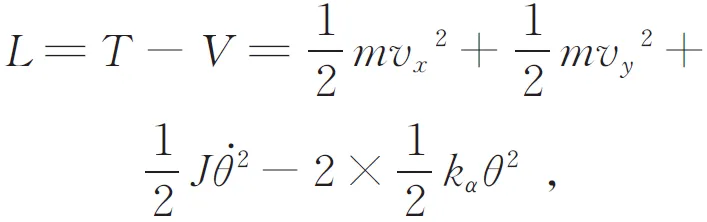
将带入Lagrange方程得到：

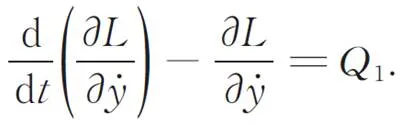
化简后得到：

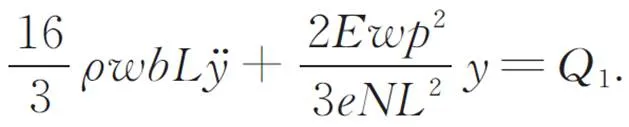
最终，得到柔性刀架的第一阶固有频率表达式为：

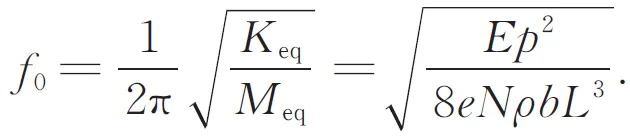
4 FTS柔性刀架多目标优化设计与有限元仿真

4.1　基于遗传算法改进的BP神经网络的柔性机构多目标优化设计

由前文分析可知，行程和工作频率是FTS两个最重要的指标，但增大行程会降低工作频率，因此需要对柔性刀架进行多目标优化设计，在满足行程要求的基础上实现更高的工作频率。本文的FTS柔性刀架多目标优化设计采用改进的BP神经网络算法，该算法可以简化优化过程。通过建立柔性刀架的结构参数和性能指标之间的映射关系，并借助ANSYS仿真结果训练关系模型，即可在设定目标值后一次求解出对应的结构参数［20-21］。

表1优化变量的取值范围

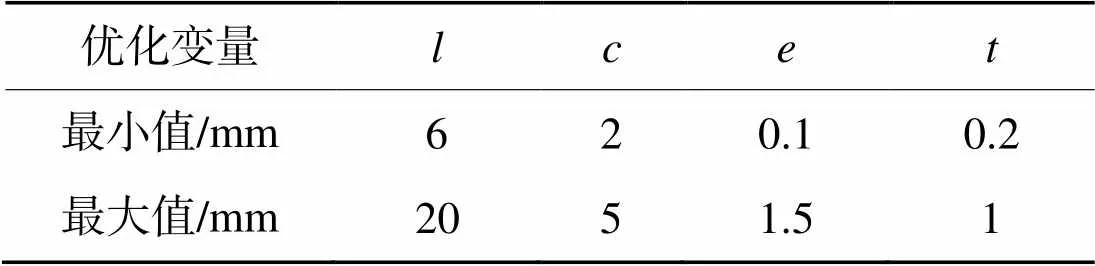
Tab.1　Range of optimized variables

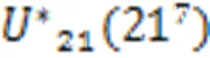
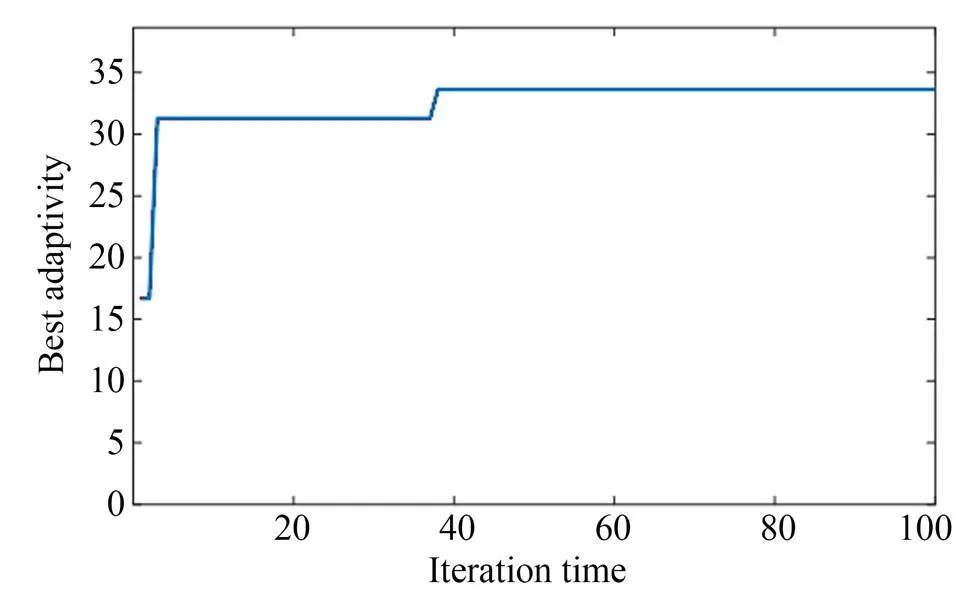
图5　最佳适应度进化曲线

本文使用的压电陶瓷促动器的最大推力为1 800 N，垂直刚度为120 N/μm。压电陶瓷促动器的实际工作频率能达到谐振频率的1/4～1/3，所选取的PEA谐振频率为40 kHz，标称行程为9 μm。考虑到工作频率和谐振频率的关系以及PEA的位移损失现象，设计目标的一阶固有频率为8 kHz，最大实际行程为7 μm，通过MATLAB求解改进的BP神经网络算法，得到最终的结果为：=8.926 8 mm，=1.119 6 mm，=1.149 1，=1 mm。以上参数构成的柔性铰链换入笛卡尔系后化简得到对应的表达方程为：

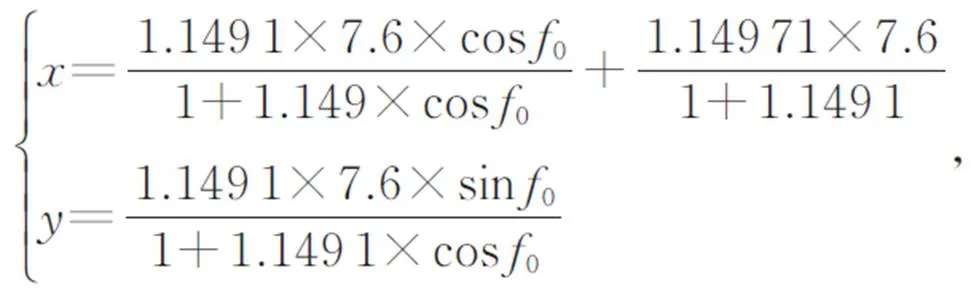
4.2　有限元仿真

为了评估柔性刀架的优化效果，根据实际安装情况固定柔性机构，在分析位移和应力时，在刀架外侧的6个螺栓孔处施加固定约束，对运动台内侧面中心点施加1 800 N的最大静态推力。图6（a）为仿真得到的变形分布，可以得到运动方向的刚度61.926 N/μm，实际位移量约为6 μm，与设计目标值存在约1 μm的偏差。对固有频率进行仿真时，在6个螺栓孔处施加固定约束而不施加其他外力，边界条件设置完成后运行求解。图6（b）显示了柔性机构的模态形状，得到柔性刀架的第一阶固有频率为8 242 Hz，与目标值存在约242 Hz的偏差。有限元仿真结果与目标参数较符合，从而可验证优化模型的有效性。从仿真结果中可知，柔性机构的非工作方向没有产生寄生运动，表明对称的结构设计消除了柔性刀架工作过程中在非期望运动方向的耦合误差。

图6　柔性刀架仿真结果

柔性刀架变形的应力分布如图7所示。由图可知，当机构位移最大时，最大应力出现在柔性铰链中间对称位置的最外层薄壁处，最大应力为239 MPa，远小于柔性刀架材料（65Mn弹簧钢）的屈服强度784 MPa，有效保证了机构在不失效的情况下完成所给定的运动任务。

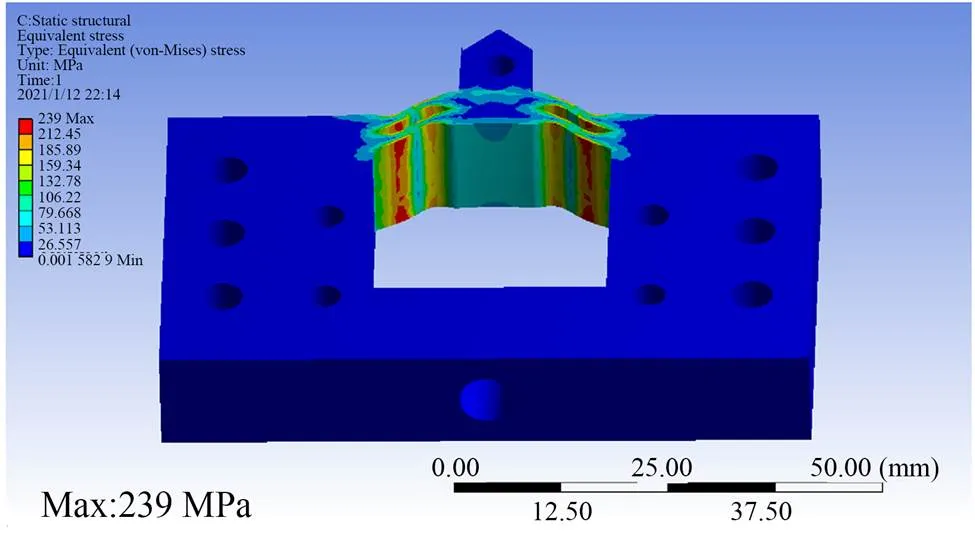
图7　柔性刀架变形应力分布

5 样机性能测试

为了测试FTS的行程，使用频率10 Hz、电压10 V的正弦波指令来驱动FTS，振动轨迹如图8所示。此时FTS的振幅约为6.4 μm，理论设计行程约为7 μm，与理论值存在0.6 μm的误差，其主要原因是实际情况下柔性机构和基座之间是非刚性连接，即连接螺钉的弹性变形导致实际行程略有减小。

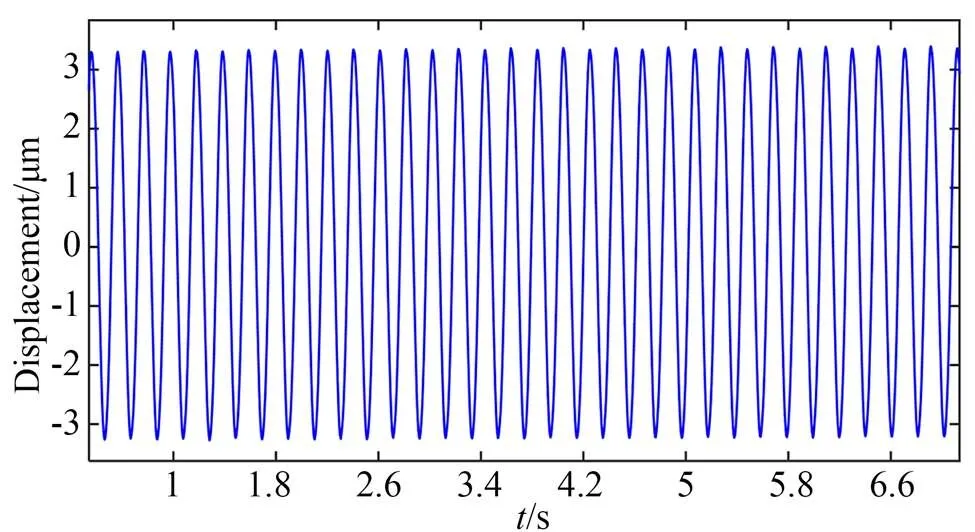
图8　FTS的振动轨迹

为了获得FTS装置的阶跃响应特征，使用PI控制器驱动FTS装置进行测试，理想运动位移设定为3 μm。如图9所示，FTS装置上升至理论位置的时间约为1.6 ms，此外，观察到约3%的幅值超调现象，效果较好。由该测试结果可知，所研制的FTS装置能够实现对刀具轨迹信号的快速平稳响应。

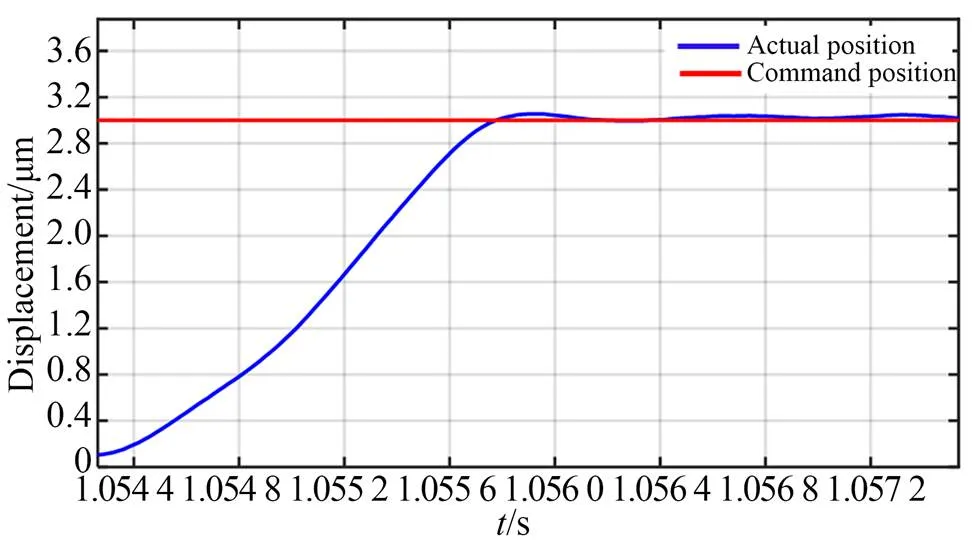
图9　FTS对激励信号的响应曲线

对FTS装置进行动力学性能测试，扫描激励是通过施加一个固定电压为10 V，偏置为0 V的命令信号，考虑到FTS设计的一阶固有频率为8 kHz，测试频率采用10～17 kHz之间线性变化的正弦波激励信号，分别记录下柔性机构的输入和输出振幅，输入-输出比值如图10所示。可以看出，一阶固有频率约为7 660 Hz，二阶固有频率约为11 060 Hz，三阶固有频率约为15 860 Hz。所得到的第一阶固有频率与设计值相差300 Hz，误差比例约为4.25%，与仿真值相差582 Hz，误差比例为7.3%。

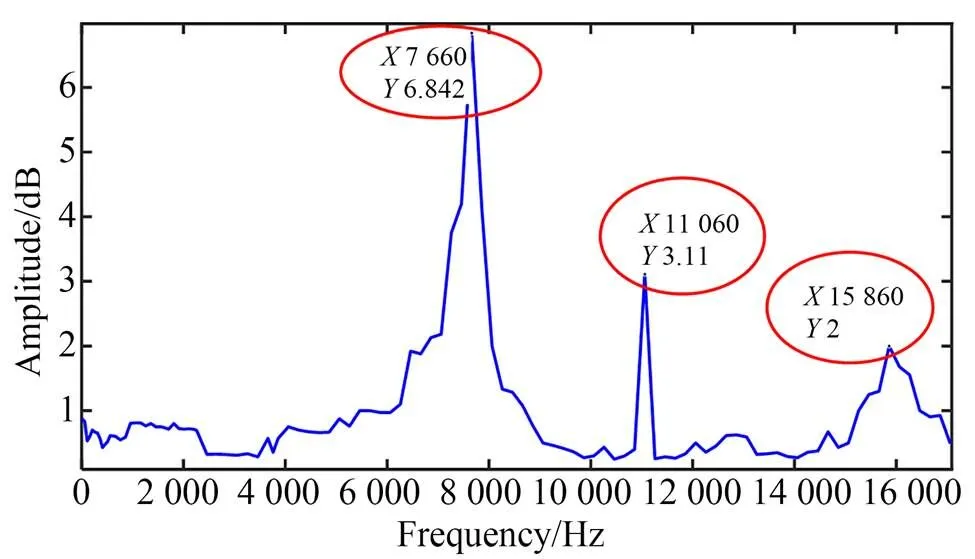
图10　FTS幅频特性曲线

为了实现纳米尺度刀具的定位及切削功能，机构的运动分辨率为其主要性能指标之一。为了测试机构的运动分辨率，本文进行阶梯型激励试验测试，所获得的机构运动响应如图11所示。可以看出，该机构的运动分辨率为12 nm，能够满足超精密加工要求。

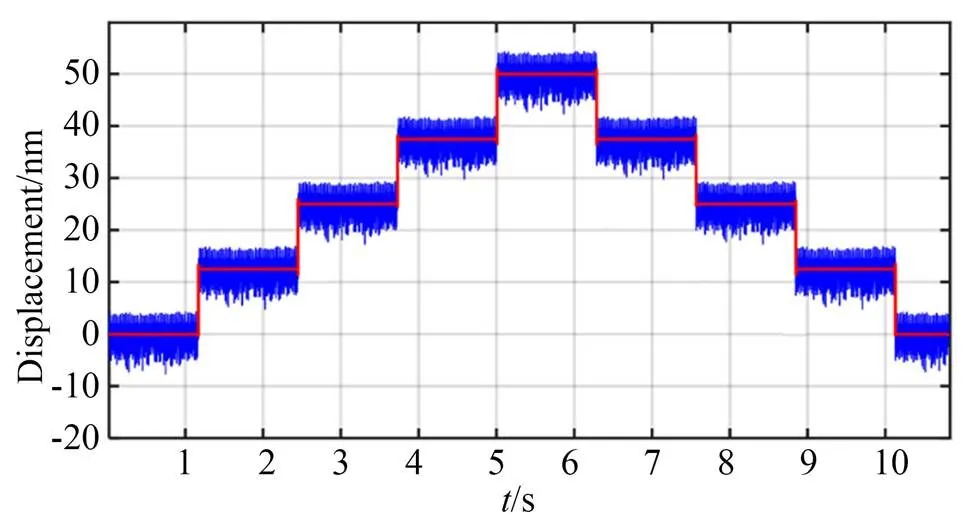
图11　FTS运动分辨率

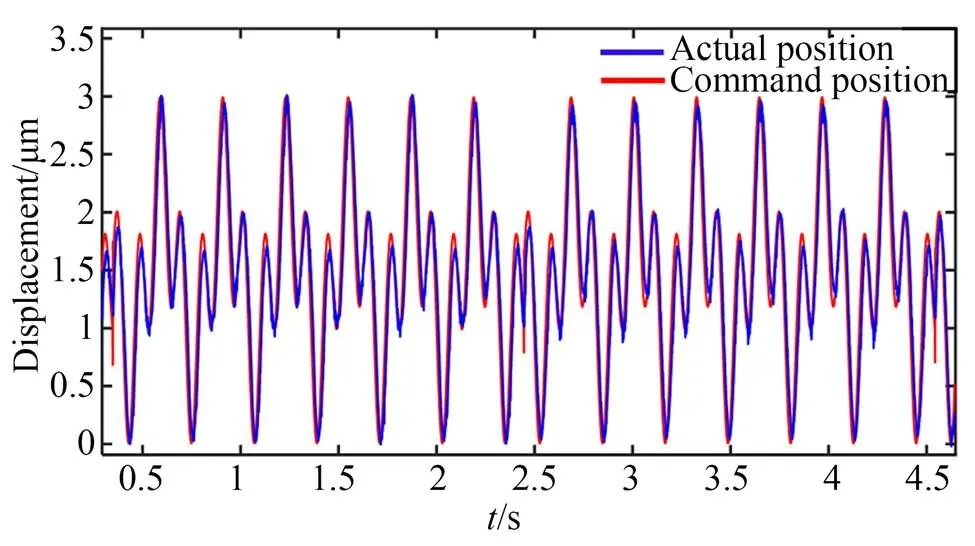
图12　FTS轨迹跟踪性能

图12和图13分别表示FTS系统对混合多种频率成份轨迹的跟踪结果，刀具的实际运动轨迹与理想轨迹吻合较好，其跟踪误差约为0.2～0.3 μm，约占相应行程的5%。由此可知，该伺服系统的轨迹跟踪精度极大程度上依赖于其运动频率，高频运动会导致跟踪误差增大，需要通过设计控制算法补偿和改进跟踪精度。

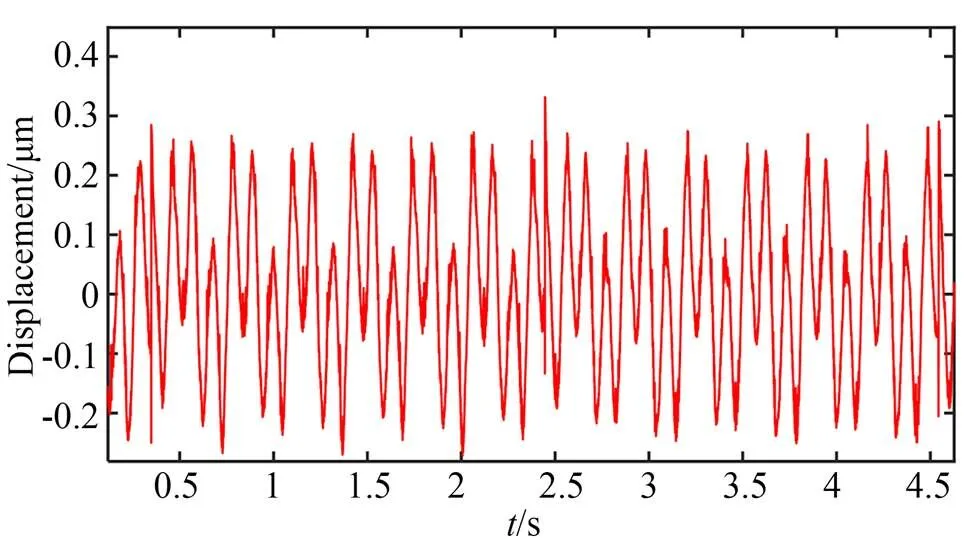
图13　FTS轨迹跟踪误差

6 典型微结构切削实验

为了验证研制的FTS装置对微结构表面加工的稳定性，本文进行了微结构面切削实验。实验在美国超精密复合加工机床 Precitech Nanoform X上进行，FTS装置安装在机床的B轴工作台，实验装置如图14所示。切削过程中，工件随着主轴转动，同时在轴方向移动，FTS装置沿机床轴以30 Hz频率产生振动，带动金刚石刀具产生往复运动加工微结构表面。金刚石刀具的圆弧半径1.032 3 mm，前角和后角分别为0°和5°，工件选用直径12 mm的紫铜棒材，切削深度为5 μm。通过白光干涉仪观测表面形貌，如图15所示，表面轮廓均为规则的波形，进一步验证了本文所设计的FTS具有稳定的加工性能。

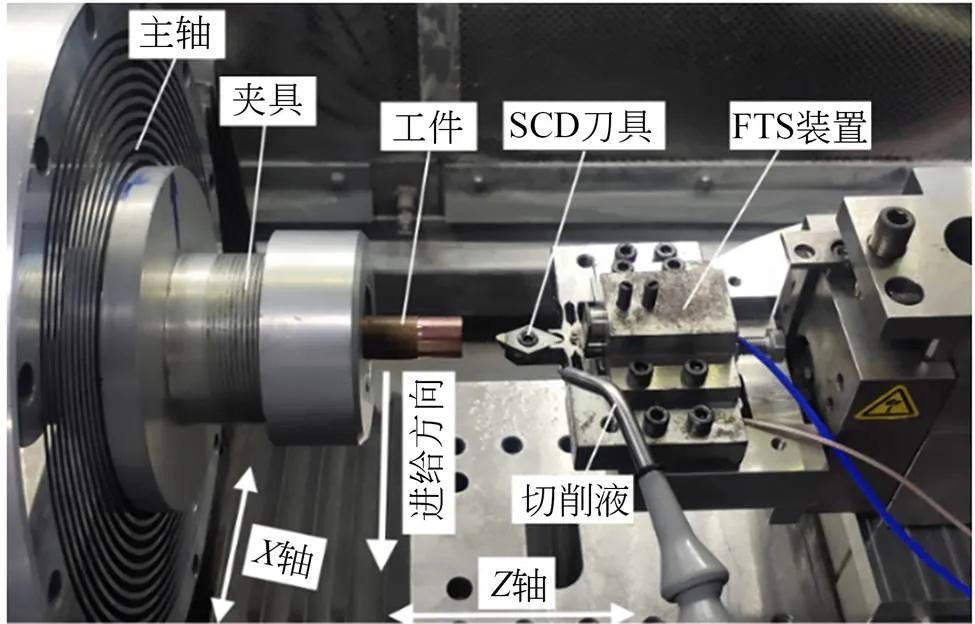
图14　微结构面切削实验装置示意图

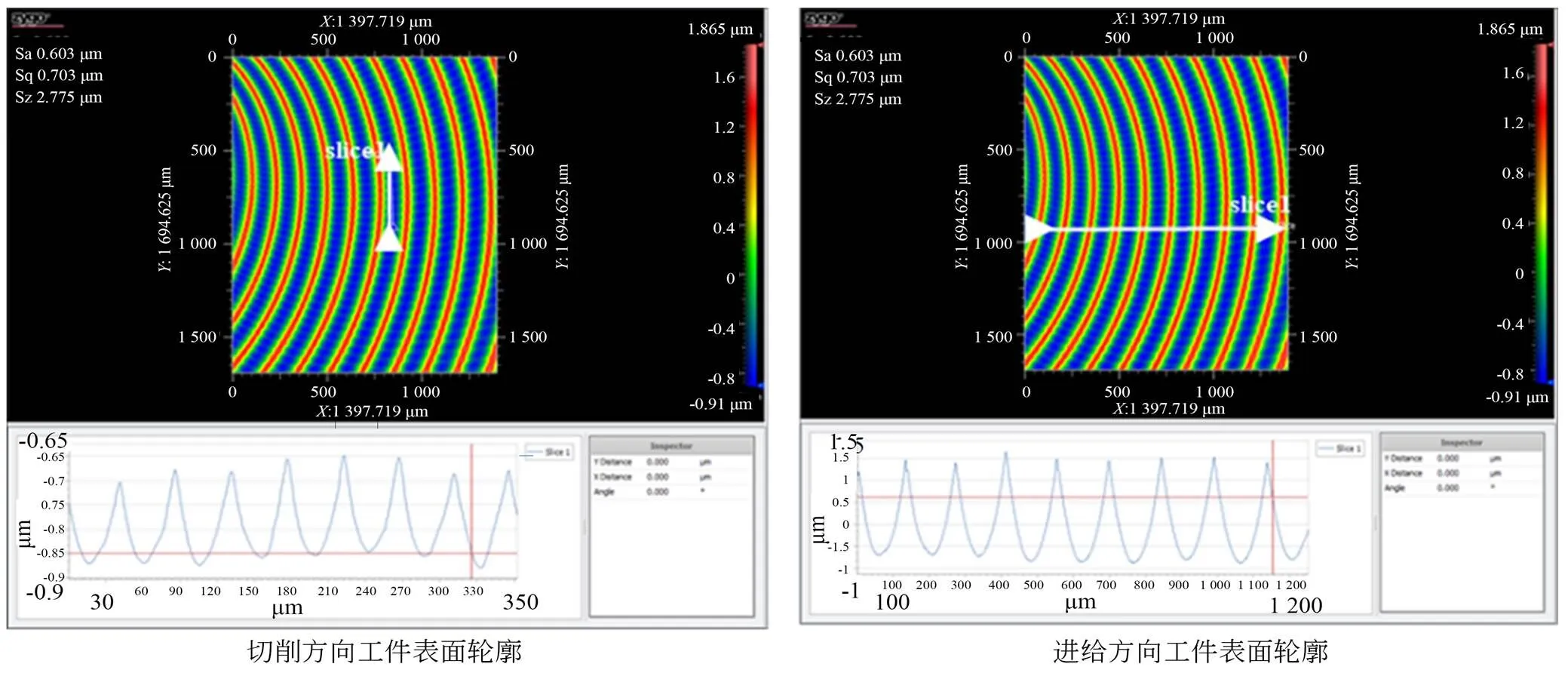
图15　微结构成形表面的微观轮廓

7 结　论

本文提出了一种紧凑的FTS装置，通过仿真模拟、参数优化制造了实验样机，并对样机进行了性能测试。测试结果表明：所设计的机构行程约为6.4 μm，固有频率超过7.6 kHz，带宽约为85 Hz。开环阶跃响应测试结果表明：对激励信号的响应时间约为1.6 ms，拥有较快的响应速度，存在约3%的幅值超调，样机能够实现对激励信号的快速平稳响应。阶梯型激励实验结果表明，装置的运动分辨率约为12 nm。混合多种频率成份轨迹的跟踪结果显示，其跟踪误差约为0.2～0.3 μm，约占相应行程的5%。利用实验样机进行微结构切削验证实验，结果表明：FTS装置加工得到的微结构表面具有良好的面形特征。该装置具有稳定的工作性能和加工能力，满足对超精密功能元件的加工要求。

［1］ PATTERSON S R， MAGRAB E B. Design and testing of a fast tool servo for diamond turning［J］.， 1985， 7（3）： 123-128.

［2］ MOON J H，LEE B G. Modeling and sensitivity analysis of a pneumatic vibration isolation system with two air Chambers［J］.， 2010， 45（12）： 1828-1850.

［3］闫鹏，李金银. 压电陶瓷驱动的长行程快刀伺服机构设计［J］. 光学精密工程， 2020， 28（2）： 390-397.

YAN P， LI J Y. Design of piezo-actuated long-stroke fast tool servo mechanism［J］.， 2020， 28（2）： 390-397. （in Chinese）

［4］ WANG J J， DU H H， GAO S M，. An ultrafast 2-D non-resonant cutting tool for texturing micro-structured surfaces［J］.， 2019， 48： 86-97.

［5］王贵林，唐力，左莉，等. 快速刀具伺服系统加工误差的超前补偿修正［J］. 制造技术与机床， 2020（3）： 50-53.

WANG G L， TANG L， ZUO L，. Correction of machining error of fast tool servo system by using lead compensating method［J］.， 2020（3）： 50-53. （in Chinese）

［6］刘晓飞，张堃，杨绍奎，等. 基于压电液压的快速刀具伺服系统研究［J］. 制造技术与机床， 2020（1）： 83-87.

LIU X F， ZHANG K， YANG SH K，. Research of fast tool servo system based on piezoelectric hydraulic［J］.， 2020（1）： 83-87. （in Chinese）

［7］ SENCER B， ISHIZAKI K， SHAMOTO E. High speed cornering strategy with confined contour error and vibration suppression for CNC machine tools［J］.， 2015， 64（1）： 369-372.

［8］ ZHU Z W， TONG Z， TO S，. Tuned diamond turning of micro-structured surfaces on brittle materials for the improvement of machining efficiency［J］.， 2019， 68（1）： 559-562.

［9］ ZHAO D P， ZHU Z H， HUANG P，. Development of a piezoelectrically actuated dual-stage fast tool servo［J］.， 2020， 144： 106873.

［10］ HUSSAIN I， XIA W， ZHAO D，. Multi-physical design and resonant controller based trajectory tracking of the electromagnetically driven fast tool servo［J］.， 2020. 9. 28：1-11.

［11］ ZHU Z W， DU H H， ZHOU R J，. Design and trajectory tracking of a nanometric ultra-fast tool servo［J］.， 2020， 67（1）： 432-441.

［12］ TAO Y D， ZHU Z W， XU Q S，. Tracking control of nanopositioning stages using parallel resonant controllers for high-speed nonraster sequential scanning［J］.， 2021， 18（3）： 1218-1228.

［13］ ZHOU R J， ZHU Z H， KONG L B，. Development of a high-performance force sensing fast tool servo［J］.， 1068（99）： 1.

［14］ ZHU Z W， ZHOU X Q， LIU Z W，. Development of a piezoelectrically actuated two-degree-of-freedom fast tool servo with decoupled motions for micro-/nanomachining［J］.， 2014， 38（4）： 809-820.

［15］ PHAM H H， CHEN I M. Stiffness modeling of flexure parallel mechanism［J］.， 2005， 29（4）： 467-478.

［16］刘柯佳，金栋平，纪斌.杠杆式柔性铰链微位移放大机构优化设计［C］. 中国力学大会-2015论文集， 2015： 256.

LIU K J， JIN D P， JI B. Optimal design of lever-type flexure hinge micro-displacement amplifying mechanism［C］.2015， 2015： 256. （in Chinese）

［17］江晓阳，陈定方. 基于ANSYS的差动式位移放大机构性能分析［J］. 湖北工业大学学报， 2010， 25（4）： 77-79.

JIANG X Y， CHEN D F. Analysis of characteristic of differential displacement amplifier based on ANSYS［J］.， 2010， 25（4）： 77-79. （in Chinese）

［18］ LI Y M， XU Q S. Development and assessment of a novel decoupled XY parallel micropositioning platform［J］.， 2010， 15（1）： 125-135.

［19］朱志伟. 散射抑制车削新方法及装置研究［D］. 长春：吉林大学，2013.

ZHU ZH W.［D］. Changchun： Jilin University， 2013. （in Chinese）

［20］秦宇，冯之敬. 基于人工神经网络的柔性铰链结构动力修改［J］. 航空精密制造技术， 2006， 42（5）： 25-27.

QIN Y， FENG ZH J. Structural dynamic modification of flexure hinge structure based on artificial neural network［J］.， 2006， 42（5）： 25-27. （in Chinese）

［21］杨海威，詹永麒，乔俊伟，等. 基于结构的神经网络优化结构参数的应用［J］. 系统仿真学报， 2003， 15（8）： 1116-1119.

YANG H W， ZHAN Y Q， QIAO J W，. Application in structural parameter optimization by using architecture-based neural network［J］.， 2003， 15（8）： 1116-1119. （in Chinese）

Optimal design of high frequency and high precision fast tool servo system

ZHANG Jianguo1，LI Jiang1，HUANG Kai1，ZHENG Zhengding1，YANG Hui2，XU Jianfeng1*

（1，，430074，；2，100076，），：

An innovative design for a fast tool servo （FTS） system exhibiting high response frequency， high precision， and a high driving force was proposed herein. A flexible hinge fitted with a generalized conic line was applied to construct a novel flexible mechanism. The coupling error of the undesired movement direction of the flexible tool holder was decreased efficiently using a symmetrically arranged structure. Moreover， the kinematic characteristics of the mechanism were comprehensively modeled. Subsequently， based on an improved BP neural network， a multi-objective optimization design for the structural size of the flexible mechanism was performed. The stroke and natural frequency of the designed structure was analyzed to balance these two conflicting design objectives. The three-dimensional model of this device was established based on structural parameters obtained via optimization. Furthermore， a finite element analysis was performed. It is demonstrated that the algorithm affords a perfect optimization effect. The flexible mechanism designed via optimization could achieve advanced performances and was hence suitable for the FTS flexible mechanism. Finally， a prototype of the device was manufactured， and performance tests were conducted to verify the optimization design process. Experimental results show that the static and dynamic performances of the proposed device satisfy the design requirements. Its natural frequency exceeds 7.6 kHz， the nominal stroke is approximately 6.4 μm， the resolution is approximately 12 nm， and the following accuracy is approximately 0.3 μm. In addition， the experimental results verify the feasibility of the designed FTS system for ultraprecision machining.

ultra-precision manufacture； fast tool servo； flexible tool holder； optimized design； finite element analysis

TH703；TP27

10.37188/OPE.20223001.0078

1004-924X（2022）01-0078-11

2021-05-24；

2020-06-28.

华中科技大学学术前沿青年团队资助项目（No. 2019QYTD12）

张建国（1985），男，河北宣化人，博士，副教授，2010年于哈尔滨工业大学获得硕士学位，2014年于名古屋大学获得博士学位，主要从事超精密制造方面的研究。E-mail：zhangjg@hust.edu.cn