离心法曲面涂胶的胶层厚度研究

2022-01-20解孟涛刘俊标王鹏飞张利新韩立

光学精密工程 2022年1期

解孟涛刘俊标*王鹏飞张利新韩立

离心法曲面涂胶的胶层厚度研究

解孟涛1，2，刘俊标1，2*，王鹏飞1，张利新1，韩立1，2

（1.中国科学院电工研究所，北京 100190；2.中国科学院大学，北京 100049）

曝光工艺中经离心涂敷后抗蚀剂胶层的均匀性对曝光线宽有很大的影响。为了得到高速旋转下抗蚀剂胶体在凹面衬底上所形成膜层厚度的均匀性，在凹面衬底上建立了非牛顿流体微元经离心旋转的流体动力学模型。根据对应的边界条件、非牛顿流体的本构方程和连续性方程，推导并得到了流体性质、曲面面形、旋转速度和时间等因素与最终厚度的关系式。使用流变仪对950 K PMMA C 2%抗蚀剂的流体性质进行标定，在凹面衬底上以旋转速度为单一变量进行离心涂胶实验，使用光谱椭圆偏振仪测量离心后随矢量半径变化的胶体厚度，并与理论推导进行对比。实验结果表明：旋转速度在2 000 r/min时，理论厚度为267 nm，实验所测厚度为230 nm，偏差比率为13.86%；旋转速度在3 000 r/min时，理论厚度为178 nm，实验所测厚度为172 nm，偏差比率为3.37%。考虑到涂胶后，前烘工艺会进一步减小胶层厚度，偏差在正常范围内。本文建立的数学模型具有较好的预见性，可以对胶体经旋转离心后的均匀性提供理论指导。

电子束曝光；离心涂胶；非牛顿流体；胶层厚度；曲面

1 引　言

曲面电子器件在集成度、空间适应性上有着平面电子器件不可比拟的优势［1］，已广泛应用于曲面天线［2］、仿生探测器［3］和智能皮肤［4］等设备。电子束直写技术利用聚焦好的电子束直接与抗蚀剂相互作用并留下图案，具有分辨率高、易于控制、操作简单等优势［5］。因此，使微纳米量级曲面电子器件的制作成为可能。抗蚀剂是电子束直写过程中图形转移的载体，抗蚀剂的涂敷是电子束直写、光学曝光等微纳米加工工艺中的关键步骤［6］，决定着后续工艺的质量，如抗蚀剂胶层中间厚、两边薄，直写出来的线条会中间宽、两边窄［7］。因此，对曲面上胶层厚度均匀性的研究在曲面微纳米器件的制作中有着重要的意义。

国外对流体在旋转圆盘上的流动很早就有研究。1921年，Kármán等［8］对无限大旋转基片上的流体流动进行研究，通过相似性原理，将柱坐标系下的N-S方程组化简为常微分方程组，简化了计算。1958年，Emslie［9］等基于流体力学得到牛顿流体在平面旋转圆盘上离心厚度的解析解。1960年，Acrivos［10］等经理论计算得到非牛顿流体在平面旋转圆盘上离心厚度的解析解。1978年，Meyerhofer［11］将胶体的蒸发考虑进离心成膜的因素，经实验得到了牛顿流体在蒸发条件下的胶厚经验模型。1979年，Givens［12］等通过多次实验发现胶层初始厚度和起始速度对最终膜层厚度的影响不大，而最终的旋转速度和胶体黏度对胶层厚度有很大的影响。1986年，范椿［13］在Acrivos的基础上，使用特征线法得到旋转平面上幂律流体受力的一般性分析解，可以计算复杂的初始条件。2005年，FENG［14］等将Emslie的模型与Dietrich Meyerhofer的蒸发模型相结合，建立牛顿流体在凹面旋涂的数学模型，对该模型进行求解得到膜层厚度的表达式。2008年，巴音贺希格［15］等在FENG的基础上，利用凹面离心涂胶实验对其模型和数学表达式进行了验证。2009年，陈龙江［16］等建立牛顿流体在凸面旋涂的数学模型，通过实验拟合验证了表达式的正确性，并得到曲率在100 mm下对应的最佳转速与时间。2011年，刘小涵［17］等对凹面向下时的离心涂胶进行分析，提出利用双轴离心法来保证成膜的均匀性。

文献［15-16］中将抗蚀剂胶体近似为牛顿流体来处理。在流体中，牛顿流体属于非牛顿流体的特例，因而针对非牛顿流体离心成膜的理论研究对胶体离心成膜厚度均匀性的指导更具有普适性。鉴于此，本文基于非牛顿流体建立在凹面内离心涂胶的数学模型，并分析求解得到经离心涂敷后的胶厚分布表达式。在电子束直写中常用的抗蚀剂为PMMA，因此以PMMA抗蚀剂为研究对象，使用流变仪测出其剪切速率与剪切力的关系。最后设计涂胶实验，根据影响胶体厚度的相关因素，利用控制变量法对理论模型进行验证，并与平面胶层的参考数据［18］进行比较来验证理论推导的正确性，从而得到胶层在凹面衬底上的均匀度。

2 理论分析

在离心涂敷的过程中，影响胶体最终厚度的主要因素有胶体的性质、匀胶机的旋转速度和旋转时间、前烘温度和烘烤时间等。由于实验情况比较复杂，因此，在建立流体动力学模型时，需要对一些条件进行简化：

（1）分析过程中的温度、湿度和大气压强不变；

（2）忽略凹面表面粗糙度和蒸发的影响；

（3）高速旋转时离心力很大，可忽略径向惯性力和科里奥利力；

（4）胶层很薄，剪切力只存在于胶体的上表面；

（5）在理论模型中未考虑前烘的影响。

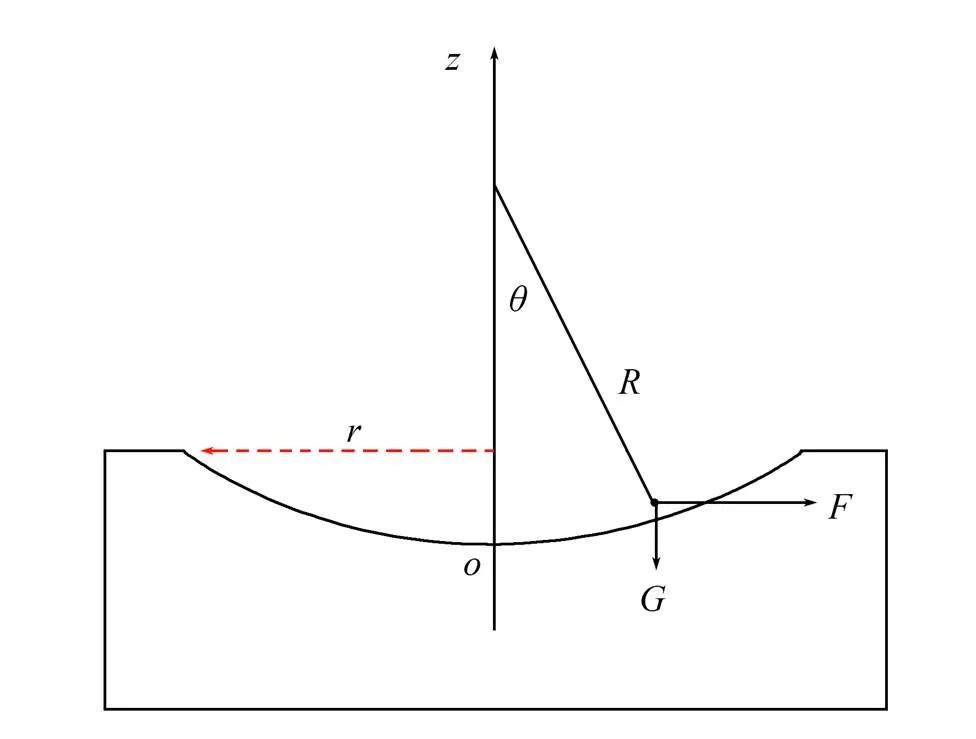
图1　非牛顿流体微元在凹面基片的受力图

基于Emslie［9］的模型，如图1所示，对单位体积的胶体微元在凹面基底上某一位置的受力进行分析，得到胶体在柱坐标系（）下离心涂胶的流体动力学方程：

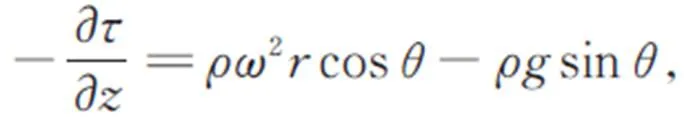
其中：∂/∂为胶体微元受到的沿曲面切向的剪切力，为胶体密度，为凹面衬底的旋转速度，为重力加速度，为胶体微元距离旋转轴的水平矢量距离，为单位体积胶体微元的高度，为转轴与胶体微元的纵向夹角，是凹面衬底的曲率半径，是胶体微元所受重力，是胶体微元所受离心力。

非牛顿流体的本构方程为：

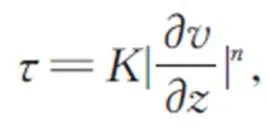
其中：和分别是非牛顿流体的稠度系数和流变指数。当=1，该流体为牛顿流体，即为牛顿流体的动力黏度。

联合式（1）和式（2）可得到非牛顿流体微元在凹面离心旋涂的流体动力学方程：

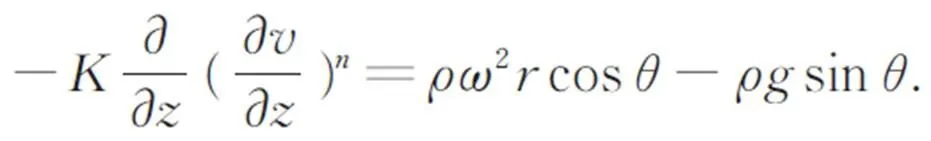
其边界条件为：

（1）当=0时，=0，即胶体的初始流速为零；

对式（3）进行两次积分，并将边界条件带入得：

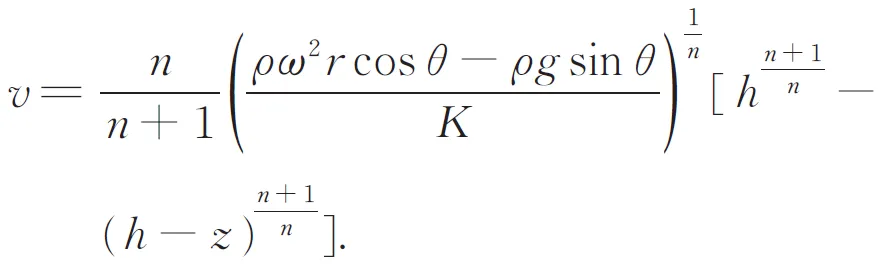
而微元截面的体积流量可以表示为：

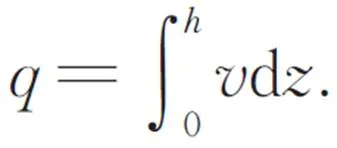
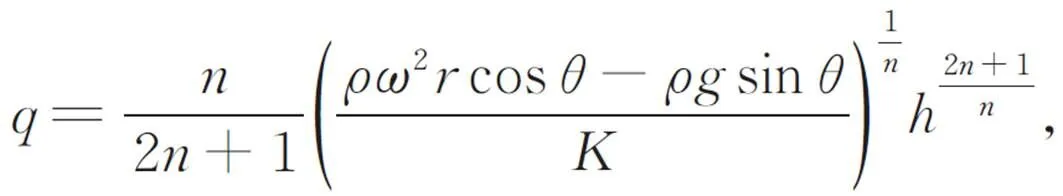
其中流体高度和体积流量的连续性方程表示为：

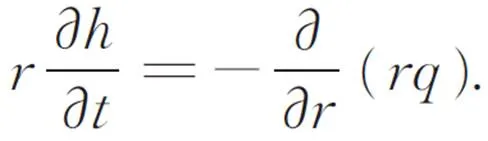
由图1可知，sin=，将式（6）带入式（7）得：

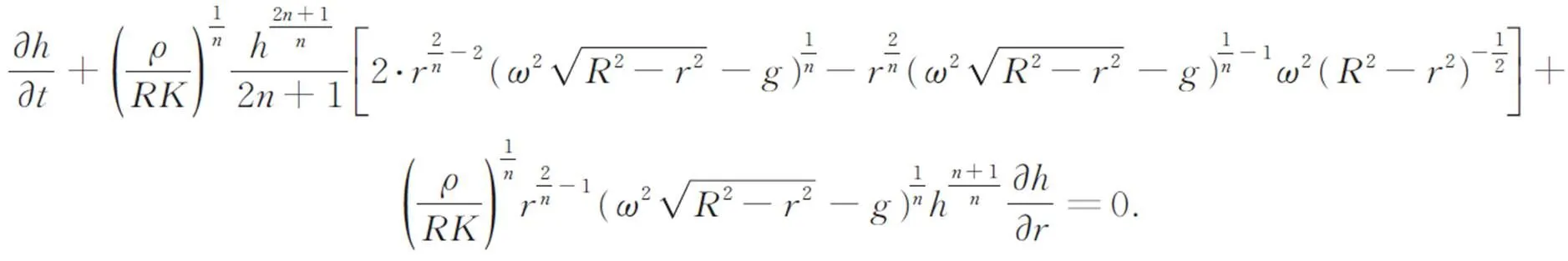
由于矢量半径与时间有关。因此，高度对时间的变化可以表示为：

联立式（8）和式（9），整理后可得：

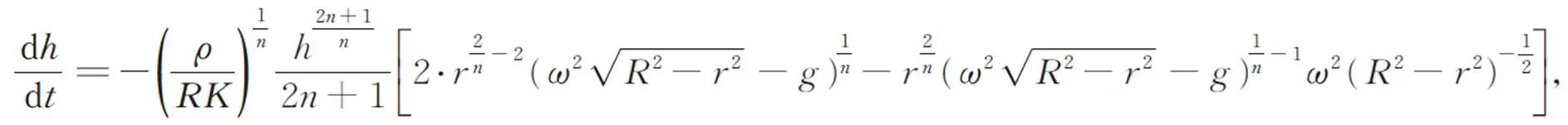
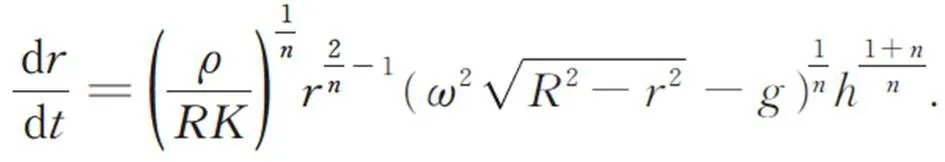
因此，对于某一矢量半径处的胶层厚度而言是固定的，式（10）经积分可得：

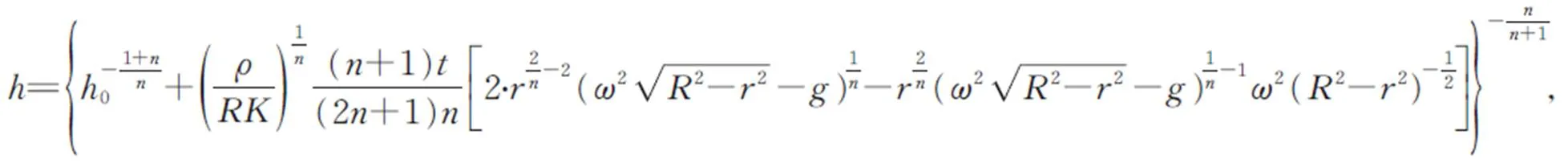
其中0为=0时初始胶层的厚度。

当流体为牛顿流体时，即：=1时，式（12）可化简为：

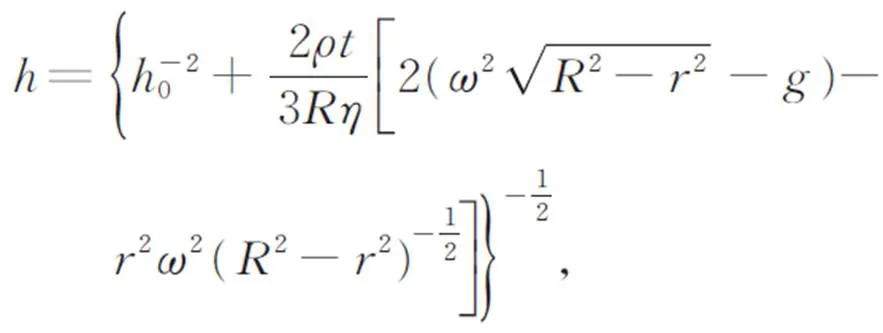
其中为胶体的动力黏度。

由式（12）可以看出，流体经离心涂敷后的厚度主要与流变指数、旋转速度、曲率半径和黏度等因素有关。当离心的转速和旋转时间恒定，凹面衬底上流体的最终厚度只与矢量半径相关。对式（12）进行数学分析发现：当=0.816时，最终厚度和初始厚度0相等。因此，设计衬底时凹面口径的半径要小于其曲率半径的0.816倍。在进行高速离心时，即2的值很大时（一般在2 000～3 000 r/min），通过计算可知重力对最终厚度并无影响，因此理论上可以忽略重力的影响。经过计算，通过改变初始膜厚不会使最终的胶层厚度发生变化，与Givens［12］的结论相同。通过计算发现，黏度大的胶体经离心后最终厚度值要大，即：黏度大的抗蚀剂经离心后的厚度比黏度小的胶层厚度大。

3 实　验

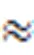
为了验证理论推导结果，在K9玻璃上制作曲率半径为100 mm，口径为50 mm的凹面。以转速为变量进行离心涂胶实验，首先对玻璃衬底进行处理，依次使用丙酮和酒精浸泡，在去离子水下冲洗并使用氮气吹干。在涂胶前，为了加快凹面基底热量的流失，先将未滴加胶体的凹面衬底放在匀胶机上空转，也可观察凹面衬底中轴与匀胶机中轴的重合情况。匀胶机第一阶段的转速为1 000 r/min，旋转时间为10 s，可以使抗蚀剂胶体均匀分布在凹面；第二阶段的转速分别设定为2 000 r/min和3 000 r/min，旋转时间为30 s，此阶段在离心力作用下胶体进一步离心，最终在凹面形成一定厚度的薄膜。匀胶后，为了防止未干的胶层因重力沿凹面出现流动，将其放入烘箱内100 °C烘烤10 min。使用光谱椭圆偏振仪（SENTECH SE 850 DUV）对胶层厚度进行测量，该光谱椭圆偏振仪可精准控制位移平台在二维平面上的移动（步长为1 mm）。

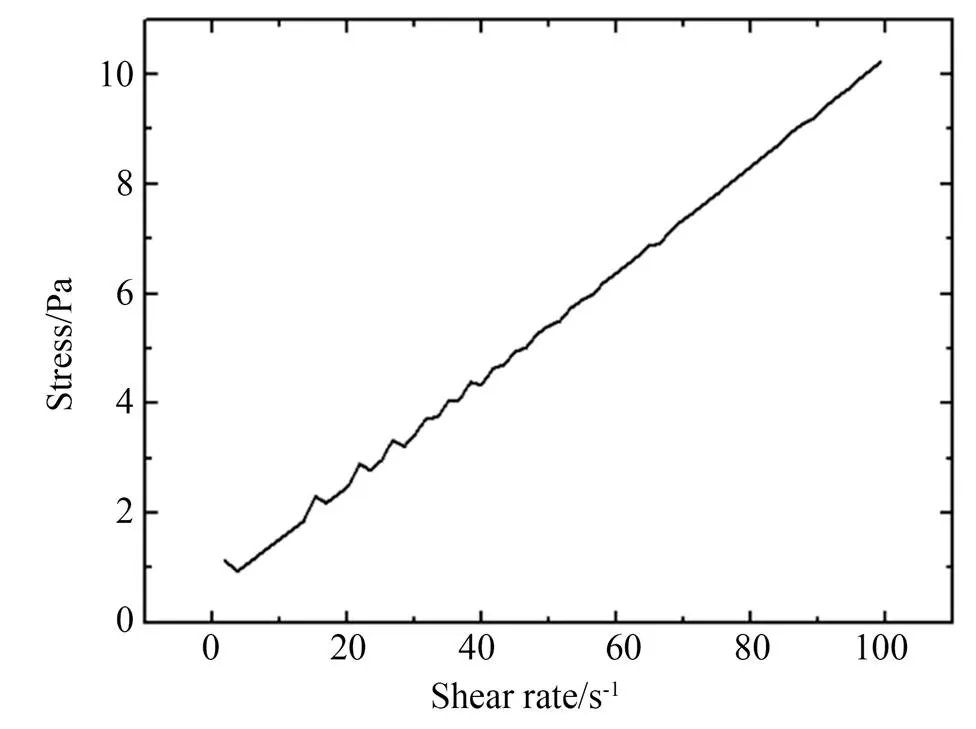
图2　抗蚀剂950 K PMMA C 2%剪切速率与剪切力的关系

光谱椭圆偏振仪是根据测量平面的条件进行设计的。测量曲面时，曲率较大或测量位置离轴心较远时，偏振光反射的法平面不再是水平面，导致偏振光的出射角度与接收器的角度偏差过大，因此接收器无法接收到偏振光，测不到对应位置的厚度。经过大量实验测试，在曲率半径为100 mm的凹面上，得到测量结果的矢量半径在±5 mm左右。图3和图4是不同转速下经实验测量得到的胶层厚度与理论计算得到的胶层厚度的对比。图中矢量半径的负和正是指测量时中轴左手边的测量点为负，中轴右手边的测量点为正。

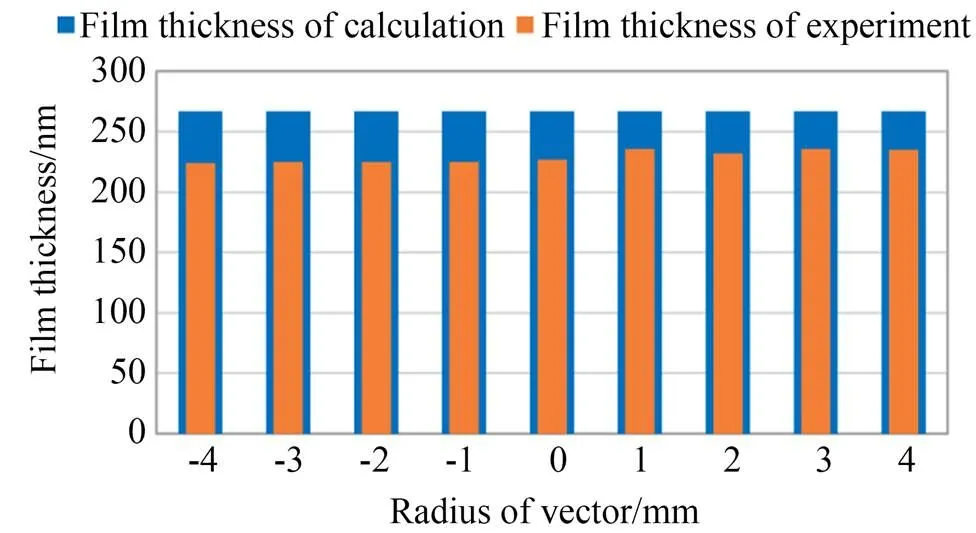
图3　转速在2 000 r/min下得到的胶层厚度对比

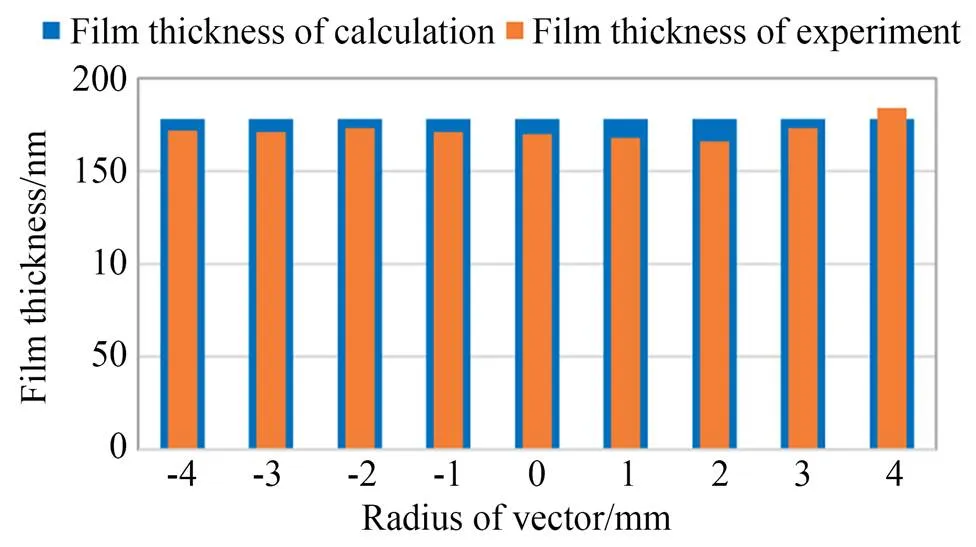
图4　转速在3 000 r/min下得到的胶层厚度对比

在图3中，理论推导值是267 nm，实验测得的平均厚度是230 nm，差值为37 nm。图中实验测量得到的矢量半径为负的胶层数据整体比矢量半径为正的胶层数据薄10 nm左右。由于在甩胶时衬底放置的中心与匀胶机的中心仅凭肉眼观察不能做到完美的重合，因此左边和右边的厚度整体上存在差距。图4中，理论推导值是178 nm，实验测得的平均厚度为172 nm，差值为6 nm。在矢量半径为4 mm的位置，实测的胶层厚度比理论厚度厚6 nm，这主要是实际测量误差导致的。

在进行胶层厚度测量前，将涂好抗蚀剂的衬底放入烘箱内，根据抗蚀剂的类型选择合适的温度和时间对其进行烘烤。这样可以降低离心涂胶时胶体内部产生的应力，并增加其黏附力，也可以防止未干的胶体出现轻微流动的现象。经过前烘，抗蚀剂中的溶剂进一步挥发，胶层的厚度变薄，导致理论计算的胶层厚度相较于实验测量的数据偏厚。经实验测得：在2 000 r/min下得到的理论值与实验值的偏差比率为13.86%；在3 000 r/min下得到的理论值与实验值的偏差比率为3.37%。在离心涂胶时，溶剂的蒸发量与前烘过程中溶剂的蒸发量的总量是恒定的，随着转速的增加，离心力和蒸发的影响会增大溶剂的蒸发，这样前烘过程中胶层的蒸发相对变小，偏差比率随之变小。

图5和图6分别是不同转速下得到的中心位置的胶层厚度与kayakuAM［18］给出的不同转速下平面胶层的指导厚度的对比。图5中，旋转速度从1 000 r/min逐步增加到4 000 r/min时，胶层厚度从540 nm左右减小到130 nm左右；图6中，旋转速度从1 000 r/min逐步增加到4 000 r/min，胶层厚度从250 nm左右减小到120 nm左右。对比图5与图6可知：旋转速度在1 000～2 500 r/min时，胶层的厚度相较于平面上厚1～2倍，由于凹面面形的存在，且离心力较小，黏性力和曲率半径起主导作用，因此理论厚度比较厚；转速大于2 500 r/min后，离心力的作用不断增大，起主导作用，凹面的面型和黏性力的影响就变小，二者的数据吻合较好。

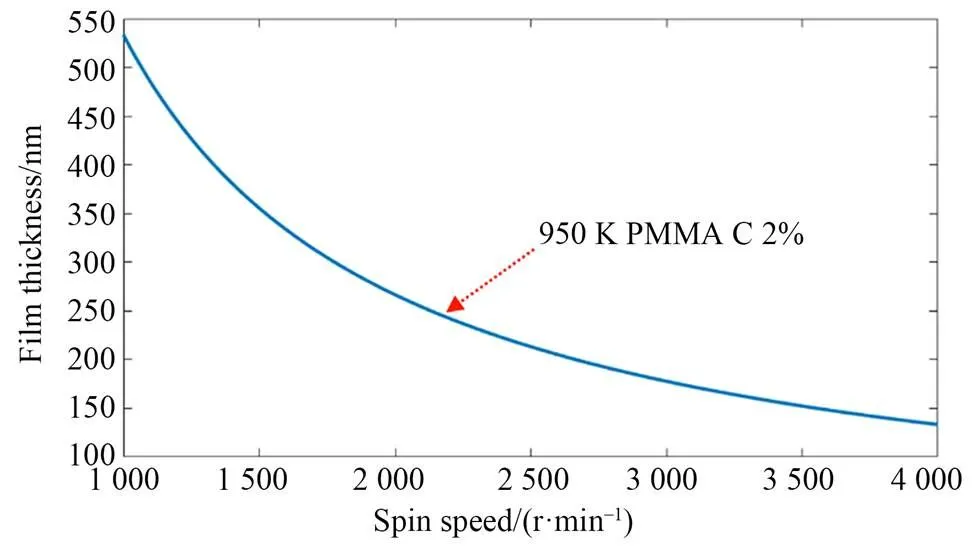
图5　不同转速下中心厚度的理论曲线

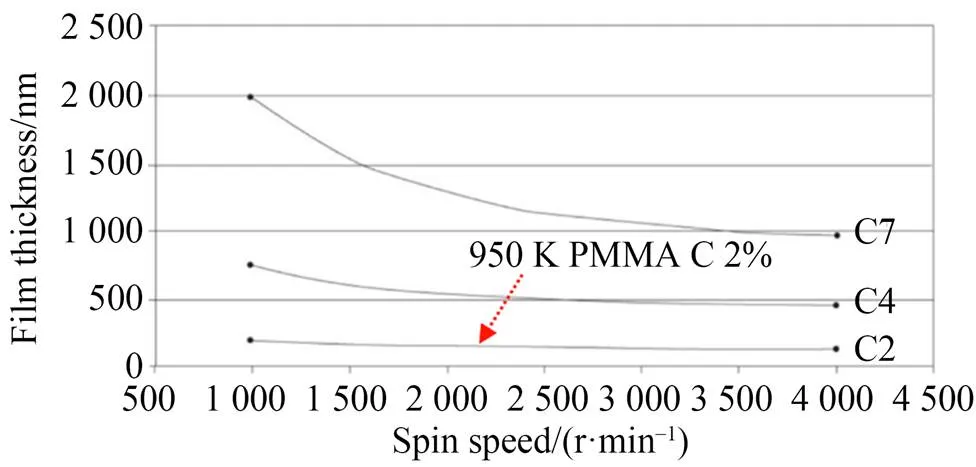
图6　kayakuAM［18］给出的参考平面厚度曲线

由于使用实验测量方法无法得到曲面上完整的厚度分布，因此设定口径为50 mm、曲率半径为100 mm、旋转时间为30 s。将参数带入式（13），使用MATLAB计算得到不同转速下抗蚀剂厚度随矢量半径的变化曲线，如图7所示。

图7　抗蚀剂厚度与矢量半径的变化关系

从图7可以看出：随着转速的增加，胶层整体的厚度不断减小，中间和边缘的厚度差值随旋转速度的增加而减小；当转速分别为2 000，3 000和4 000 r/min时，离心涂敷后胶层的中心厚度与边缘厚度理论上的差值分别为8.9，5.9和4.4 nm。由此可以看出，在增加转速的同时，厚度差也在不断减小。因此，理论上想要控制胶层的均匀性，可以尝试在高转速下通过多次离心涂胶的方法来减小差值。

4 结　论

本文基于流体力学计算得到非牛顿流体在曲面衬底上经离心旋转后胶层厚度分布随矢量半径变化的解析解，利用离心涂胶实验对解析解进行论证，结果表明在2 000 r/min转速下的理论厚度比实测厚度厚13.86%，在3 000 r/min转速下的理论厚度比实测厚度厚3.37%。由于前烘的影响，这个差距的比率在正常范围内，且随着转速的增加，差值比率在缩小与实际相符。与kayakuAM给出平面上的胶层指导厚度相比，在较高转速下，二者吻合很好。利用本文的模型通过控制转速和时间等因素可以指导固定曲率曲面胶体的涂敷。此外，理论上要在曲面上得到厚度均匀的胶体，可通过在高转速下进行多次涂胶来实现。

［1］ WU H， TIAN Y， LUO H B，. Fabrication techniques for curved electronics on arbitrary surfaces［J］.， 2020， 5（8）： 2000093.

［2］高晓峰，敖辽辉，胡蜀娟，等. 曲面曝光技术在异形曲面高精度线条制造工艺中的应用［J］. 电讯技术， 2002， 42（3）： 57-59.

GAO X F， AO L H， HU SH J，. Application of bent exposure technology in the manufacture technology of high precision line on abnormity bent surface［J］.， 2002， 42（3）： 57-59. （in Chinese）

［3］ SONG Y M， XIE Y Z， MALYARCHUK V，. Digital cameras with designs inspired by the arthropod eye［J］.， 2013， 497（7447）： 95-99.

［4］ WANG X D， DONG L， ZHANG H L，. Recent progress in electronic skin［J］.， 2015， 2（10）： 1500169.

［5］顾文琪. 电子束曝光微纳加工技术［M］. 北京：北京工业大学出版社， 2004.

GU W Q.［M］. Beijing： Beijing University of Technology Press， 2004. （in Chinese）

［6］林盛浩. 半导体匀胶系统的研究与优化设计［D］. 成都：电子科技大学，2010.

LIN SH H.［D］. Chengdu： University of Electronic Science and Technology， 2010. （in Chinese）

［7］付永启，赵晶丽. 离心式涂胶膜厚均匀性的影响因素分析［J］. 光学精密工程， 1996， 4（2）： 94-97.

FU Y Q， ZHAO J L. Analysis of effect on uniformity of photoresist layer in spin coating［J］.， 1996， 4（2）： 94-97. （in Chinese）

［8］ KÁRMÁN T V. Über laminare und turbulente Reibung［J］.-， 1921， 1（4）： 233-252.

［9］ EMSLIE A G， BONNER F T， PECK L G. Flow of a viscous liquid on a rotating disk［J］.， 1958， 29（5）： 858-862.

［10］ ACRIVOS A， SHAH M J， PETERSEN E E. On the flow of a non-Newtonian liquid on a rotating disk［J］.， 1960， 31（6）： 963-968.

［11］ MEYERHOFER D. Characteristics of resist films produced by spinning［J］.， 1978， 49（7）： 3993-3997.

［12］ GIVENS F L， DAUGHTON W J. On the uniformity of thin films： a new technique applied to polyimides［J］.， 1979， 126（2）： 269-272.

［13］范椿. 幂律流体在旋转圆盘上的流动［J］. 力学与实践， 1986， 8（4）： 31-33.

FAN CH. Flow of a power-law liquid on rotating disk［J］.， 1986， 8（4）： 31-33. （in Chinese）

［14］ FENG X G， SUN L C. Mathematical model of spin-coated photoresist on a spherical substrate［J］.， 2005， 13（18）： 7070.

［15］巴音贺希格，张浩泰，李文昊. 凹球面基底离心式涂胶的数学模型及实验验证［J］. 光学精密工程， 2008， 16（2）： 229-234.

BAYANHESHIG， ZHANG H T， LI W H. Mathematic model and experiment verification of spin-coating on concave spherical substrate［J］.， 2008， 16（2）： 229-234. （in Chinese）

［16］陈龙江，罗剑波，梁宜勇，等. 球面旋涂胶层厚度分布模型及其实验研究［J］. 光电子·激光， 2009， 20（4）： 470-474.

CHEN L J， LUO J B， LIANG Y Y，. The model of spin-coating photoresist-layer thickness on spherical surface and its experimental verification［J］.， 2009， 20（4）： 470-474. （in Chinese）

［17］刘小涵，冯晓国，赵晶丽，等. 球面旋涂光刻胶工艺［J］. 光学精密工程， 2011， 19（8）： 1810-1815.

LIU X H， FENG X G， ZHAO J L，. Process of spherical photoresist spin coating［J］.， 2011， 19（8）： 1810-1815. （in Chinese）

［18］ KAYAKUAM.［EB/OL］.（2020-07）.［2021-07］.KAM-PMMA-TDS.4.12.21.pdf （kayakuam.com）.

Research on resist-layer thickness by spin-coating on curved substrate

XIE Mengtao1，2，LIU Junbiao1，2*，WANG Pengfei1，ZHANG Lixin1，HAN Li1，2

（1，，100190，；2，100049，），：

In lithography， the uniformity of resist coating considerably affects the consistency of line width after spin-coating. To obtain homogeneity of the resist-layer thickness on the upper surface of a curved substrate， a hydrodynamic model of a non-Newtonian fluid element is first established on the surface of the curved substrate under spin-coating. According to the corresponding boundary conditions and constitutive equation and continuity equation of the non-Newtonian fluid， the relationship between the nature of the fluid， curvature radius of the surface， horizontal vector radius， rotation speed and time， and the final thickness of the fluid is deduced and obtained. Second， a rheometer is used to calibrate the fluid viscosity of 950 K PMMA C 2% resist. A spin-coating experiment is conducted on a curved substrate using rotational velocity as a single variable. After centrifugation， the thickness was measured by ellipsometry. The relationship between the resist-layer thickness and the change in the vector radius is obtained and demonstrated with theoretical results. Experimental results show that when the spin speed is 2 000 r/min， the theoretical thickness is 267 nm， measured thickness is 230 nm， and deviation ratio is 13.86%. When the spin speed is 3 000 r/min， the theoretical thickness is 178 nm， measured thickness is 172 nm， and deviation ratio is 3.37%. After spin-coating， the soft-bake will further reduce the thickness of the resist-layer，and the deviation is within the normal range. Therefore， the mathematical model can provide a theoretical guidance for homogeneity after spin-coating， and the established model has a good predictability.

electron beam lithography； spin-coating； non-Newtonian fluid； layer thickness； curved surfaces

TN305.7

10.37188/OPE.2021.0477

1004-924X（2022）01-0071-07

2021-07-18；

2021-08-09.

中国科学院科研仪器设备研制项目（No.GJJSTD20200003）；广东省重点领域研发计划资助项目（No.2020B0101320002）

解孟涛（1996-），男，河南焦作人，硕士研究生，2019年于辽宁大学获得学士学位，主要从事电子束曝光技术的研究。E-mail：jiemt@mail.iee.ac.cn