利用分部积分法求解不定积分题型探究

吴德福

(吉林建筑科技学院基础科学部，长春 130000)

1 类型总结

类型1：分部化简型。此类型可按照反三角函数、对数函数、幂函数、指数函数、三角函数的顺序，将排在前面的函数作为复杂函数u(x)，将排在后面的函数作为简单函数v′(x)，然后按照分部积分公式即可求解。

积分类型u,v的选取∫xneaxdx=1a∫xndeaxu=xn,v=eax∫xnsinaxdx=-1a∫xndcosaxu=xn,v=cosax∫xncosaxdx=1a∫xndsinaxu=xn,v=sinax

此类型有一个快速解题技巧：令u(x)=pn(x),v(n+1)=eax或v(n+1)=sinax(cosax)，按下表操作：

用法：A.推广的分部积分各项(不包括符号)为从左到右错位相乘。B.各项的符号为“+”“-”相间。C.当u=pn(x)的某阶导数为0时，求导和求原函数的工作停止。

解析：

积分类型(n≠-1)u,v的选取∫xnlnxdx=1n+1∫lnxdxn+1u=lnx,v=xn+1∫xnarcsinxdx=1n+1∫arcsinxdxn+1u=arcsinx,v=xn+1∫xnarctanxdx=1n+1∫arctanxdxn+1u=arctanx,v=xn+1

(3)被积函数只有对数函数或反三角函数：当被积函数只有反三角函数或者对数函数这一类函数时，也可采用分部积分法，将积分变量x当作v，直接使用分部积分法，操作如下。

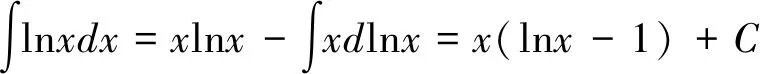
当被积函数是比较复杂的复合函数且只有一个函数时，也可尝试采用类似的方法处理。

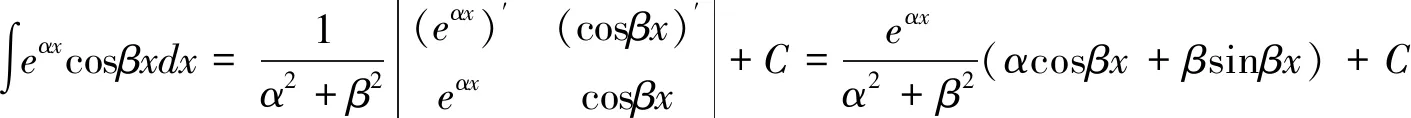
可将这个结论当作公式背诵下来，在求解类似的题目时可代入公式快算求得结果。

2 结语

希望通过总结，让学生对分部积分法的各个类型有一个整体认识，快速掌握其应用方法。